PID 算法简介
??PID算法是一种控制算法,是 Proportional(比例)、Integral(积分)、Derivative(微分)的缩写。该控制算法广泛的应用于工业控制当中。应用场景:温度控制、流量控制、液位控制等。
PID算法历史简介
??PID控制算法是基于控制理论发展起来,控制理论的历史可以追溯到古代,如我国古代的指南车、地动仪、水位仪等,都是用到了控制理论。
??最早提出PID控制理念的是瑞典裔美国人奈奎斯特,他在一篇论文当中写到了采用图形的方法来判断系统的稳定性,在他的基础上,伯德等人建立了一整套在频域范围设计反馈放大器的方法,后被用于自动控制系统的分析和设计,
直到1922年PID控制理论才首次由俄罗斯籍美国科学家尼古拉斯-米诺斯基使用在了船舶自动转向装置上的研究。
??在1936年后,PID开始广泛的用于工业控制,从洗澡水的控制到神七上天,从空调控温到导弹制导,从能源、化工到家电、环保、制造、加工、军事、航天等等,都有它的影子,都可以看到它在发挥作用。
什么是算法?
算法是指解题方案的准确而完整的描述,是一系列解决问题的清晰指令,算法代表着用系统的方法描述解决问题的策略机制(摘自百度百科)
我以为算法简单来说就是解决一个问题所采用的方法。举例:
- 百度地图搜索坐地铁去一个地方,这其实是一个图论中的最短路径问题。
- 大象的重量
- 地球的重量
PID原理
位式控制算法
工业上会有一些需求,比如将液体的温度加热控制在某个温度。传统的位式控制算法是这样做的。
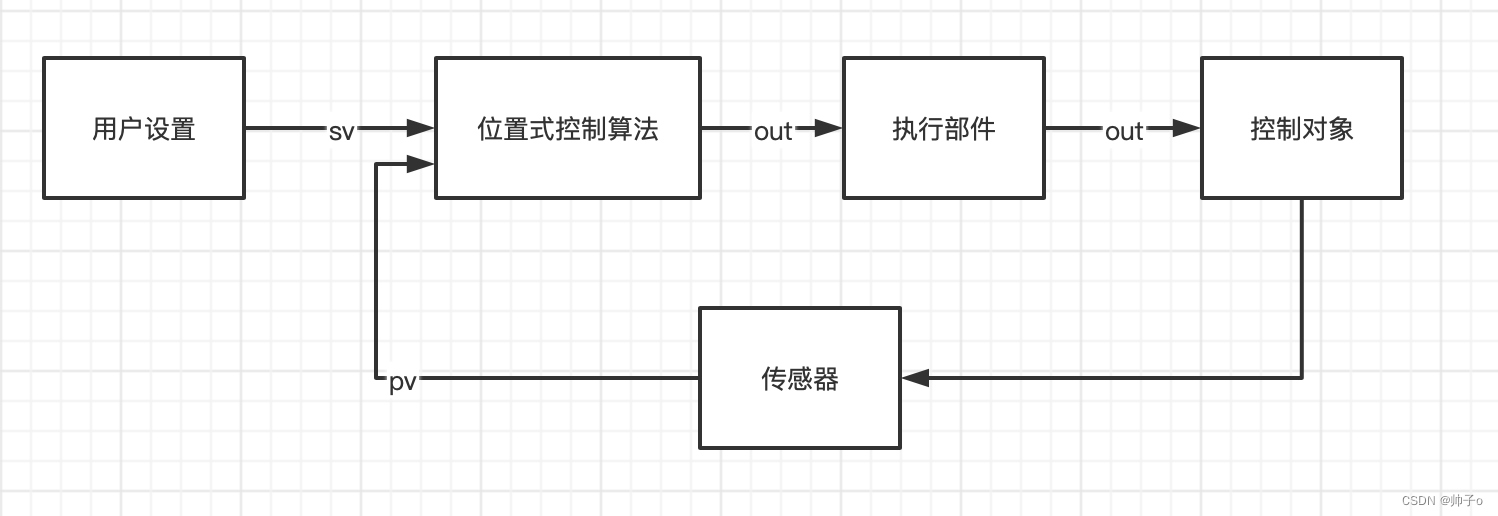
特点:
- 位式控制算法的输出信号只有H L 两种状态。
- 算法输出信号out的依据是sv、pv,既用户设定值和传感器接受到的值的比较。当pv < sv 时 输出L ,当pv >= sv时输出H。
- 只考察控制对象当前的状态。
- 开放回路控制系统
开环控制(Open Loop Control System):不将控制的结果反馈回来影响当前控制的系统。
- 闭环回路控制系统
闭环控制(Closed Loop Control System):需要将控制的结果反馈回来与希望值比较,并根据它们的误差调整控制作用的系统。
PID控制算法
为了解决位式控制算法的问题,于是我们就是用了PID控制算法,PID控制算法的原理如下:
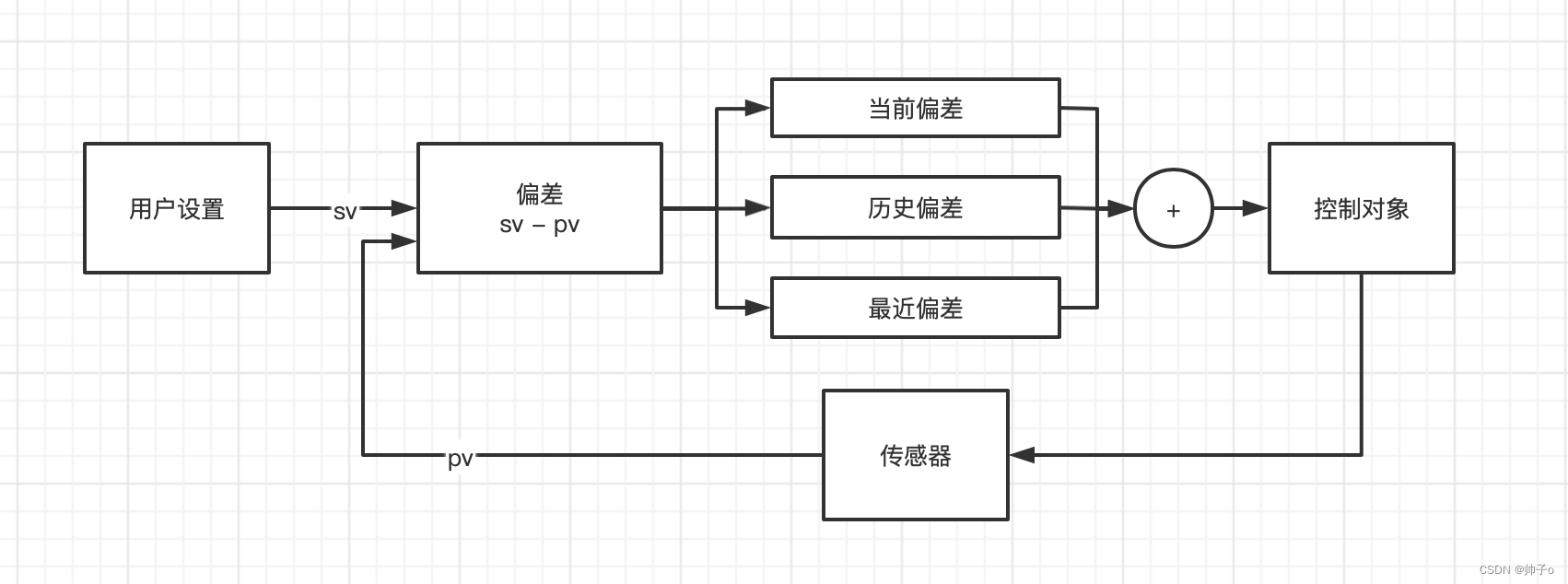
位式控制算法当中,我们知识考虑当前值与观测到的值的偏差。 而在PID算法中,又引入了历史偏差和最近偏差。将3个值共同相加作用于控制对象。这是一个比较综合的算法,能够有效的解决上面所说的问题。
PID算法的分析:
当前偏差
指的是传感器观测到的值,与用户设置的值之间的差。E = SV - PV 。这里要注意的是当前偏差是有正有负的。
E 有3种情况:
E > 0 , 表明还未达到用户设置的值
E = 0 , 正好达到
E < 0 , 超过了用户设置的值
我们用E乘以一个系数KP来作为输出值,Pout = E * KP。KP系数的作用就是增加或缩小当前偏差的比例。这种控制就称之为比例控制,也就是PID中的P控制。特点是偏差越大输出的功率就越大,偏差越小输出的功率就越小。
- 缺点
就是当E = 0 时,Pout = E * 0 ,输出功率就变成了0,系统也就不工作了,温度就会又降下来。 解决方法是增加一个常数项 Pout = E * KP + out0 , 保证当偏差为0的时候,还有一定的功率作用于控制对象。
但偏差的问题还是存在,还是会产生震荡。
历史偏差
指的是从该系统启动开始,一直到此时此刻所产生的偏差之和。
历史偏差之和integral = E1 + E2 + … + Ek。 (k表示当前时刻)
历史偏差表示的是历史上达标与否的一个情况。integral也有3种情况:
integral > 0 ,累计的越大,表明长时间未达标。
integral = 0 , 非常理想的状态,几乎很少见。
integral < 0 ,表明长时间是超标的。
Iout = integral * KI 作为输出。KI就是积分系数 (类似于数学上的积分,累加求和)
- 缺点
单纯的积分控制,表明历史上的状态,而不考虑当前偏差的状态。这会导致当前实际情况其实未达标。所以要考虑历史和当前两方面的原因, 于是就将Pout + Iout 的和作为输出。
历史偏差还有一个作用就是纠正稳态误差。稳态误差是当系统状态稳定时,实际值与用户设定值之间的误差。
最近偏差
指的是最近两次采样值偏差的偏差,这里有点不太好理解。 比如上一时刻离目标值差了70,用Ek-1表示,当前时刻离目标值差了50,用Ek表示, 那么最近一次的偏差derivative = Ek - Ek-1 。套用刚才的值就是derivative = 50 - 70 = -20 。
这里其实表示的是变化的速度, 如果此刻离目标值差了10 ,那么derivative = 10 - 70 = -60 。 说明温度急剧上升。 起到防止过冲的作用。derivative也有3种情况,
derivative > 0,
derivative = 0,偏差趋势没有变化。也就是保持一个恒定的变化率。
derivative < 0,
这是一个有预见性的一个算法。会根据速度的变化而调整输出,当变化速度过就会抑制out。将derivative也乘以一个系数作为输出,
Dout = derivative * KD。 KD就叫做微分系数。(类似于数学上的求导数,表示此刻的变化率)。
PID算法的数学模型
再回看PID算法图,将三者相加作为输出。就是我们的PID算法,
out = E * KP + integral * KI + derivative * KD + out0
他的数学模型是:
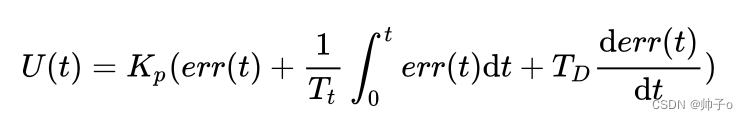
定积分的几何意义是求面积,如不规则梯形的面积。这是一种近似的求解方法。
导数的意义是表明在某一点的变化率。如变速直线运动下某时刻的速度。温度变化的速度等。
这是一个连续量公式,计算机不能处理连续量,所以要将他它离散化。
- 连续
连续型随机变量是指如果随机变量X的所有可能取值不可以逐个列举出来,而是取数轴上某一区间内的任一点的随机变量。例如,一批电子元件的寿命、实际中常遇到的测量误差等都是连续型随机变量 - 离散
如果随机变量X只可能取有限个或至多可列个值,则称X为离散型随机变量。如硬币的两面,骰子,开关灯。
离散化后的公式为:
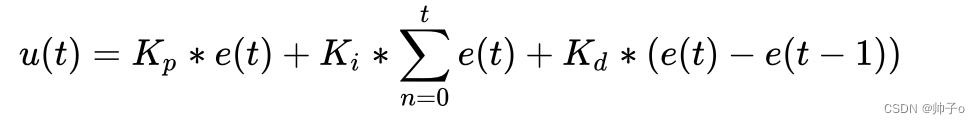
用程序表示就是上面所得到的公式
out = E * KP + integral * KI + derivative * KD + out0
积分中存在的两个问题
PID程序代码
void myPID(int setpoint)
{
while ( some condition )
{
error = setpoint – sensor value;
integral = integral + error;
if (error = 0 or passes setpoint)
integral = 0;
if (error is outside useful range)
integral = 0;
derivative = error – prevError;
prevError = error;
power = error*kP + integral*kI + derivative*kD;
wait 15 mSec;
}
}
KP、KI、KD参数的整定
性能与指标
First of all, we’ll look into some factors that determine the behaviour and
performance of our PID controller in reality:
? Rise time – the time it takes to get from the beginning point to the target
point
? Overshoot – how far beyond the target your system goes when passing the
target
? Settling time – the time it takes to settle back down when encountering a
change
? Steady-state error – the error at the equilibrium, when it’s stopped moving
? Stability – the “smoothness” of the motion
Now, let’s check out how these are effected by an increase in our three constants:
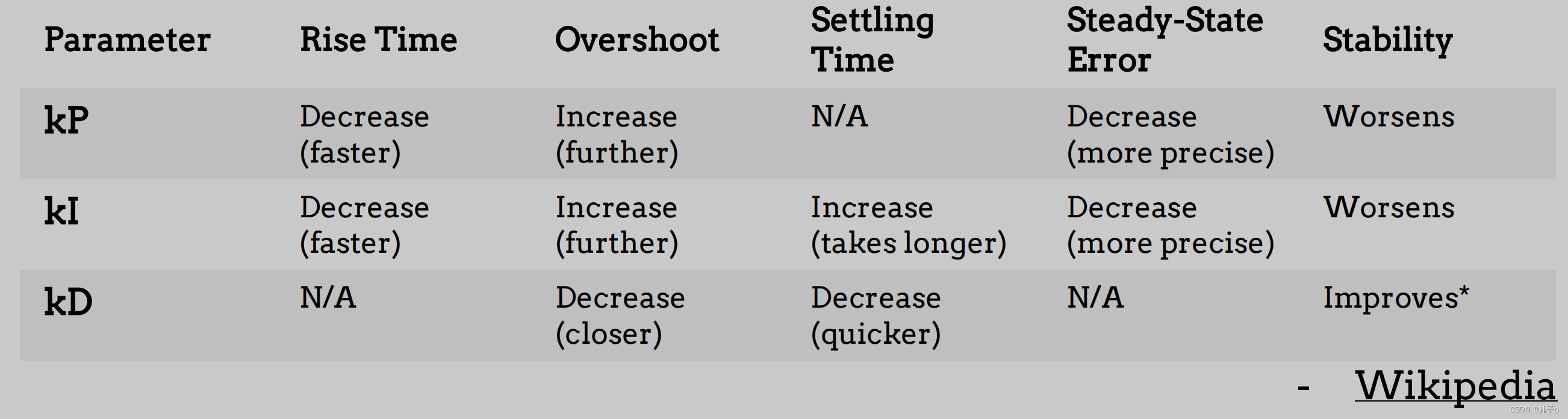
整定过程
PID调参口诀
参数整定找最佳,从小到大顺序查;
先是比例后积分,最后再把微分加;
曲线振荡很频繁,比例度盘要放大;
曲线漂浮绕大湾,比例度盘往小扳;
曲线偏离回复慢,积分时间往下降;
曲线波动周期长,积分时间再加长;
曲线振荡频率快,先把微分降下来;
动差大来波动慢。微分时间应加长;
理想曲线两个波,前高后低4比1;
一看二调多分析,调节质量不会低;
若要反应增快,增大P减小I;
若要反应减慢,减小P增大I;
如果比例太大,会引起系统振荡;
如果积分太大,会引起系统迟钝。
结论
祝福
合抱之木,生于毫末;
九层之台,起于累土;
千里之行,始于足下。
参考资料
- An Introduction to PID Controllers :http://georgegillard.com
- PID专题课程
- PID算法温控项目
- PID算法的数学推导
- PID控制算法介绍
- 深入浅出PID算法 : https://www.jianshu.com/p/6118f6dfbf8c
- PID算法 : https://www.bilibili.com/video/BV1cE411n7Ef?spm_id_from=333.880.my_history.page.click&vd_source=21f86fbb5dec75882ef4e695aaec9ba6