[数据结构与算法]最长递增子序列及最优解、动物总重量问题

题目

求一个数组中最长递增的子序列的长度，子序列不要求连续

• 通过一个dp数组来记录每个数组中以该元素结尾的最长子序列，则第i个元素结尾的最长子序列=0～i-1范围内，比第i个元素小的，dp中存储的长度最大的+1
• 第一个元素dp[0]=1,第二个元素,如果比第一个元素大，则dp[1]=2否则为1，…

复杂度为O(n*n)的解：

let arr = [2, 7, 5, 3, 6, 4, 5, 6, 1];

//O(n*n)
function maxSubLen(arr) {
  if (arr == null || arr.length == 0) {
    return 0;
  }
  let n = arr.length;
  //dp数组存储数组中以每个元素结尾的最长子序列值
  let dp = [];
  dp[0] = 1;
  let max = dp[0];
  for (let i = 1; i < n; i++) {
    let pre = 0;
    //遍历每个元素之前的元素，查找所有比该元素小的，且dp长度最大的那个
    for (let j = 0; j < i; j++) {
      if (arr[j] < arr[i]) {
        pre = Math.max(pre, dp[j]);
      }
    }
    //记录以该元素结尾的最长子序列值
    dp[i] = pre + 1;
    //查重记录的值中最大的
    max = Math.max(max, dp[i]);
  }
  return max;
}
console.log(maxSubLen(arr));

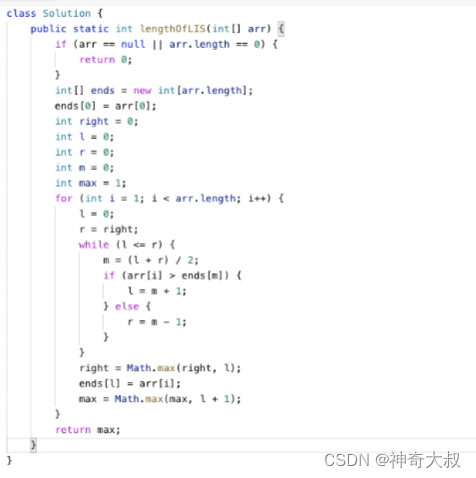
复杂度为O(n*logn)的解：

• 再添加一个数组ends，用来帮助dp存储以当前元素结尾的子序列的长度，ends中存储的是当前元素，索引为当前元素的子序列的长度，每遍历一个元素时，会查找ends中第一个比该元素大的元素，然后将元素放置在该位置，如果没有找到，则说明序列长度应该增加，则数组长度加1，放在末尾

  • 假设数组为 [2, 7, 5, 3, 6, 4, 4, 6, 1];
  • ends[0]=2,dp[0]=2;第二个元素为7，ends中没有比7大的，则数组扩容，序列长度加1，ends[1]=7,dp[1]=2;
  • 第三个元素为5，ends中第一个比5大的是7，则将7覆盖成5，ends[1]=5,d[2]=2
  • 第四个元素是3，ends中第一个比3大的是5，则将5覆盖成3，ends[1]=3,d[3]=2
  • 第五个元素是6，ends中没有比6大数，则数组扩容，序列长度加1，ends[2]=6,dp[4]=3;
  • 第六个元素是4，ends中第一个比4大的是6，则将6覆盖成4，ends[2]=4,d[5]=3；
  • 第七个元素是4，因为相同不能算递增序列，所以相同的数直接覆盖ends中相同的元素，ends[2]=4,d[6]=3；
  • 第八个数是6，ends中没有比6大数，则数组扩容，序列长度加1，ends[3]=6,dp[7]=4;
  • 第九个数是1，ends中第一个比1大的是2，则将2覆盖成1，ends[0]=1,d[8]=1

• 因为数组中没有比当前元素大的就扩容+1，表明序列长度+1；数组中能找到第一个比当前元素大的就替换，索引+1即为当前元素结尾的序列长度。因此ends中的元素是有序递增的，在查处时即可通过二分查找，使得时间复杂度为O(logN)；

• 而ends数组的存放逻辑，即对应了人类查找的思维，比如[1,3,4,2];ends前三个数[1,3,4]，第四个数2对应的递增序列应该为1，2，要放在ends中的位置即为第一个比2大的位置[1,2,4]，索引+1即为长度

• 换种说法：每当ends数组中找到一个比当前元素大的元素，说明以当前元素结尾的序列和之前断掉了（不能构成递增序列），需要重新计算，而新的序列就是之前ends中比当前元素小的那些元素加上当前元素构成的序列

let arr = [2, 7, 5, 3, 6, 4, 4, 6, 1];

function maxSubLen2(arr) {
  if (arr == null || arr.length == 0) {
    return 0;
  }
  let n = arr.length;
  let dp = [];
  let ends = [];
  dp[0] = 1;
  ends[0] = arr[0];
  //ends数组有效区
  //0到validSize-1的范围二分
  let max = dp[0];
  let validSize = 1;

  for (let i = 1; i < n; i++) {
    let cur = arr[i];
    
    //二分查处第一个比当前元素大的元素位置
    let endsi = find(ends, validSize, cur);
    //-1表示没有找到，说明ends数组有效区里都是小于num的，说明需要扩充有效区
    if (endsi == -1) {
      ends[validSize++] = cur;
      //扩容后的长度就是新增元素的序列长度
      dp[i] = validSize;
    } else {
      ends[endsi] = cur;
      //第一个比当前元素大的元素位置+1，就是以当前元素结尾的序列长度
      dp[i] = endsi + 1;
    }
    max = Math.max(max, dp[i]);
  }
  return max;
}

//ends数组有效区里查找>=num最左的位置，没有则返回-1,二分查找
function find(ends, size, num) {
  let left = 0;
  let right = size - 1;

  let min = -1;
  let mid = 0;
  //left即代表第一个比当前元素大的元素位置
  while (left <= right) {
    mid = left + parseInt((right - left) / 2);

    if (ends[mid] > num) {
      right = mid - 1;
    } else {
      //等于当前元素的元素，直接替换位置即可
      if (ends[mid] == num) {
        left = right = mid;
        break;
      }
      left = mid + 1;
    }
  }
  // console.log(left);
  // console.log(right);
  //没有找到，说明数组元素都比当前元素小
  if (left == size) {
    return -1;
  }
  return left;
}

题目

有n个动物重量分别是a1、a2、a3…an,这群动物一起玩叠罗汉游戏,规定从左往右选择动物，每只动物左边动物的总重量不超过自己的重量，返回最多能选多少个动物，求一个高效的算法。比如有7个动物，从左往右重量依次为: 1, 3, 5, 7, 9, 11, 21 ，则最多能选5个动物:1, 3, 5, 9, 21，注意本题给的例子是有序的，但是实际给定的动物数组，可能是无序的,
要求从左往右选动物，且不能打乱原始数组

• 左边动物的总重量不超过自己的重量，说明一定是个递增序列，题目也变成了求最长递增子序列
• 和上面解法类似，同样通过一个dp数组记录每个以该元素结尾的最长长度，一个ends数组，用来记录索引+1对应长度的最小重量的和，同时索引+1的长度就为dp对应元素的长度
  • 根据题目给的内容，第一个元素为1，dp[0]=1,ends[0]=1;第二个元素为3，ends中没有比它大的元素，则数组扩容，dp[1]=2,ends[1]=3+1=4,表示以3结尾的序列的总重量
  • 第三个元素为5，ends中没有比它大的元素，则数组扩容，dp[2]=3,ends[2]=3+1+5=9,表示以5结尾的序列的总重量
  • 第四个元素为7，查找到ends数组中有比7大的，查询从数组右边开始第一个比7小的元素的位置，即ends[1]=4,因为4+7>9,说明以7结尾的序列总重量大于了以5结尾的总重量，又因为要求选取最多的数量，所以应该总重量越小越好，所以第四个元素不进行替换，只记录长度，固dp[3]=3（ends[1]的总长度2+1）,ends[2]=9;
  • 第五个元素为9，ends中没有比它大的元素，则数组扩容，dp[4]=4,ends[3]=3+1+5+9=18,表示以9结尾的序列的总重量
  • 第六个元素为11，查询从数组右边开始第一个比11小的元素的位置为9，即ends[2]=9因为9+11>18,说明以11结尾的序列总重量大于了以9结尾的总重量，又因为要求选取最多的数,所以应该总重量越小越好，所以第六个元素不进行替换，只记录长度，固dp[5]=4（ends[2]的长度+1）,ends[3]=18;
  • 第七个元素为21，ends中没有比它大的元素，则数组扩容，dp[6]=5,ends[4]=18+21=39,表示以21结尾的序列的总重量；固最多选择5个
• 因为ends中存储的内容表示，每个索引+1长度的序列的最小总重量，所以如果找不到比当前元素大的，说明数组应该扩容，序列长度+1，固数组一定是个递增有序的；如果找到有元素比当前元素大，说明当前元素不能链接上，需要新建一个序列，而新建的序列就为第一个比当前元素小的（总重量比当前元素小）和当前元素组成的序列，同时需要满足新序列的总重量是相同长度条件下最小的，才能替换ends中对应索引的总重量。

let arr3 = [1, 3, 5, 7, 9, 11, 21];

function maxSubLen3(arr) {
  if (arr == null || arr.length == 0) {
    return 0;
  }
  let n = arr.length;
  let dp = [];
  let ends = [];
  dp[0] = 1;
  ends[0] = arr[0];
  //ends数组有效区
  //0到validSize-1的范围二分
  let max = dp[0];
  let validSize = 1;

  for (let i = 1; i < n; i++) {
    let cur = arr[i];

    let endsi = find2(ends, validSize, cur);

    //ends数组有效区里都是小于num的，说明需要扩充有效区
    if (endsi == validSize - 1) {
      ends[validSize] = ends[validSize - 1] + cur;
      dp[i] = ++validSize;
    } else {
      //根据查找到的第一个比该元素小的元素和该元素的和（累加重量），如果小于已有的，则进行替换
      if (ends[endsi] + cur < ends[endsi + 1]) {
        ends[endsi + 1] = ends[endsi] + cur;
        // endsi + 1 表示该元素的位置，再+1表示长度
        dp[i] = endsi + 1 + 1;
      } else {
        dp[i] = endsi + 1 + 1;
      }
    }
    max = Math.max(max, dp[i]);
  }

  return max;
}

//ends数组有效区里第一个比num小的位置
function find2(ends, size, num) {
  let left = 0;
  let right = size - 1;

  let mid = 0;
  let res = 0;
  while (left <= right) {
    mid = left + parseInt((right - left) / 2);

    if (ends[mid] <= num) {
      res = mid;
      left = mid + 1;
    } else {
      right = mid - 1;
    }
  }
  return res;
}
console.log(maxSubLen3(arr3));