一：算法思想

硬聚类：传统K-均值算法中，每个对象只能从属于所有类别中的一类，称之为硬聚类。这种聚类方法会带来一个问题：所有的对象对于计算聚类中心的贡献都是相同的，也就是说，对于从属于一个类的所有元素，算法是无法将其区分开来的。这种分配方式在处理一些复杂数据集合（例如数据有重叠）会造成类别指派不合理
软聚类：一个对象可以从属于多个类别的聚类方法

模糊K-均值算法（FCM算法）：对于每个类别，对象都对应一个取值范围在[0,1]的数值，它表示该对象从属于某一类别的可能性。一个对象对于所有类别的对应取值和应该为1。在更新簇中心点的过程中，该数值就反映了该对象对于这一类的贡献程度，根据贡献程度的不同，反映出对象更倾向于分配到哪个类别中

FCM算法与K-均值算法的目标函数类似

$J_{m}=\sum_{k=1}^{N}\sum_{j=1}u_{ij}^{m}||x_{i}-c_{j}||^{2}，1\leq m <\infty$

其中

$m (> 1)$ ：模糊系数
$N$ ：样本数
$C$ ：聚类中心数
$c_{j}$ ：第 $j$ 个聚类中心
$x_{i}$ ：第 $i$ 个样本
$u_{ij}$ ：样本 $x_{i}$ 对聚类中心 $c_{j}$ 的隶属度，也即 $x_{i}$ 属于 $c_{j}$ 的概率。显然有 $\sum\limits_{j=1}^{C}u_{ij}$ =1

FCM算法通过更新 $u_{ij}$ 和 $c_{j}$ 来迭代优化目标函数

$u_{ij}=\frac{1}{\sum\limits_{k=1}^{C}(\frac{||x_{i}-c_{j}||}{||x_{i}-c_{k}||})^{\frac{2}{m-1}}}$

$c_{j}=\frac{\sum\limits_{i=1}^{N}u_{ij}^{m}x_{i}}{\sum\limits_{_{i=1}}^{N}u_{ij}^{m}}$

FCM算法的收敛条件一般设置为两次迭代过程中计算的 $S S E$ 差值，其中 $\xi$ 是预先设定好的容忍误差，当两次迭代过程中计算的 $S S E$ 差值小于该预设值时，判定算法收敛

$E(t)=||SSE^{t}-SSE^{t-1}||<\xi$

二：算法流程

初始化隶属度矩阵 $U^{0}$ ：若有 $N$ 个样本，指定类别个数为 $C$ ，则隶属度矩阵应为 $N$ × $C$
根据公式更新聚类中心 $c_{j}$
根据公式更新隶属度矩阵（注意保存更新前的隶属度矩阵）
判断是否收敛，若收敛则停止迭代，反之返回步骤2

三：Python实现

import numpy as np
import copy

#  欧氏距离
def distance(data, centroid):
    return np.sqrt(np.sum(np.power(data-centroid, 2)))


def fcm(data_set, m, k, eps):
    example_nums = np.shape(data_set)[0]  # 样本数量
    cluster = np.zeros(example_nums)

    # 初始化隶属度矩阵
    random_mat = np.random.rand(example_nums, k)  # 生成随机矩阵
    random_mat_sum = 1 / np.sum(random_mat, axis=1)  # 求每一行的和
    membership_mat = np.multiply(random_mat.T, random_mat_sum)  # 使隶属度矩阵每一行和为1
    membership_mat = membership_mat.T
    membership_mat_old = np.zeros((example_nums, k))  # 便于迭代

    # 进行迭代，更新隶属度矩阵和聚类中心
    while True:
        centorids = np.empty((k, np.shape(data_set)[1]))
        # 由公式计算簇中心
        for j in range(k):
            centorids[j] = np.dot(membership_mat[:, j]**m, data_set) / (np.sum(membership_mat[:, j]**m))
        membership_mat_old = membership_mat.copy()

        # 根据公式计算新的隶属度矩阵
        for i in range(example_nums):
            for j in range(k):
                for z in range(k):
                    membership_mat[i, j] += ((distance(data_set[i], centorids[j])) / distance(data_set[i], centorids[z])) ** (2 / (m-1))
        membership_mat = 1 / membership_mat

        #  判断是否收敛
        if np.max(np.abs(membership_mat - membership_mat_old)) < eps:
            cluster = np.argmax(membership_mat, axis=1)
            return centorids, cluste

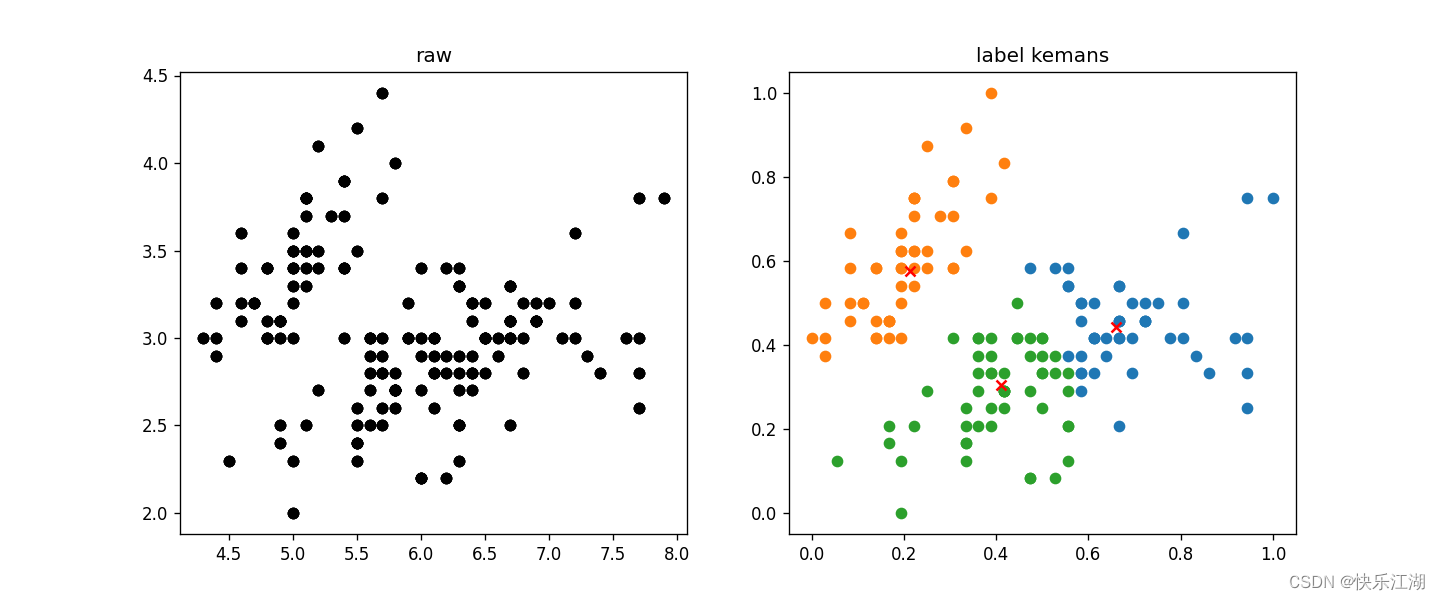
四：效果展示

import pandas as pd
import matplotlib.pyplot as plt
import FCM
import numpy as np

Iris_types = ['Iris-setosa', 'Iris-versicolor', 'Iris-virginica']  # 花类型
Iris_data = pd.read_csv('dataSet/Iris.csv')
# x_axis = 'PetalLengthCm'  # 花瓣长度
# y_axis = 'PetalWidthCm'   # 花瓣宽度
x_axis = 'SepalLengthCm'  # 花萼长度
y_axis = 'SepalWidthCm'  # 花萼宽度

examples_num = Iris_data.shape[0]  # 样本数量
train_data = Iris_data[[x_axis, y_axis]].values.reshape(examples_num, 2)  # 整理数据

# 归一化
min_vals = train_data.min(0)
max_vals = train_data.max(0)
ranges = max_vals - min_vals
normal_data = np.zeros(np.shape(train_data))
nums = train_data.shape[0]
normal_data = train_data - np.tile(min_vals, (nums, 1))
normal_data = normal_data / np.tile(ranges, (nums, 1))

#  训练参数
k = 3  # 簇数
max_iterations = 50  # 最大迭代次数
centroids, cluster = FCM.fcm(normal_data, 2, k, 1e-6)


plt.figure(figsize=(12, 5), dpi=80)

#  第一幅图是已知标签或全部数据
plt.subplot(1, 2, 1)

for Iris_type in Iris_types:
        plt.scatter(Iris_data[x_axis], Iris_data[y_axis], c='black')
plt.title('raw')

# 第二幅图是聚类结果
plt.subplot(1, 2, 2)
for centroid_id, centroid in enumerate(centroids):  # 非聚类中心
    current_examples_index = (cluster == centroid_id).flatten()
    plt.scatter(normal_data[current_examples_index, 0], normal_data[current_examples_index, 1])

for centroid_id, centroid in enumerate(centroids):  # 聚类中心
    plt.scatter(centroid[0], centroid[1], c='red', marker='x')
plt.title('label kemans')
plt.show()