[数据结构与算法]数据结构与算法二：时间/空间复杂度（complexity）

从架构的角度来看，可扩展性是指更改 app 的难易程度。从数据库的角度来看，可伸缩性是指在数据库中保存或检索数据所需的时间快慢程度。

对于算法，可扩展性是指随着输入大小的增加，算法在执行时间和内存使用方面的表现情况。

当处理少量数据时，不好的算法（时间、空间代价昂贵）可能仍然让人感觉执行速度很快。然而，随着数据量的增加，昂贵的算法将会变得很糟糕。只是它会变得多糟糕呢？如何量化这个糟糕程度是我们需要了解的一项重要技能。

时间复杂度

对于少量数据，由于现代硬件的速度，即使是最昂贵的算法也可能看起来执行速度很快。然而，随着数据的增加，昂贵算法的成本将变得越来越明显。时间复杂度是随着输入大小的增加运行算法所需时间的度量。

恒定时间

恒定时间算法是指无论输入大小怎样，都具有相同运行时间的算法。

我们来看以下代码：

func checkFirst(names: [String]) {
  if let first = names.first {
    print(first)
  } else {
    print("no names")
  }
}

names 数组的大小对该函数的运行时间没有影响。无论数组输入是 10条数据还是 1000 万条数据，此函数都只检查数组的第一个元素。 这是一个简单的时间复杂度示例：

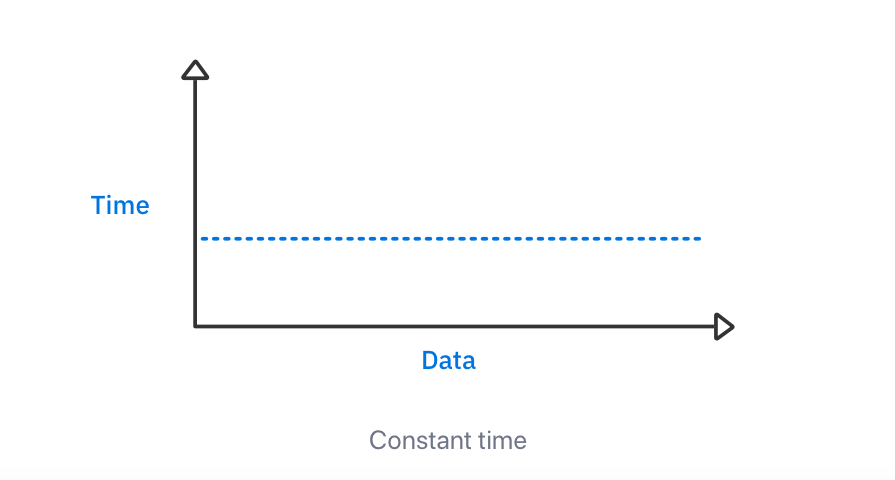
随着输入数据的增加，算法所花费的时间不会改变。

为简洁起见，程序员使用一种称为 Big O 表示法来表示各种时间复杂度的大小。常数时间的大 O 表示法是 O(1)。

Linear time

再看以下代码段：

func printNames(names: [String]) {
  for name in names {
    print(name)
  }
}

此函数打印出字符串数组中的所有名称。随着输入数组大小的增加，for 循环的迭代次数也会增加相同的数量。

这种行为称为线性时间复杂度：

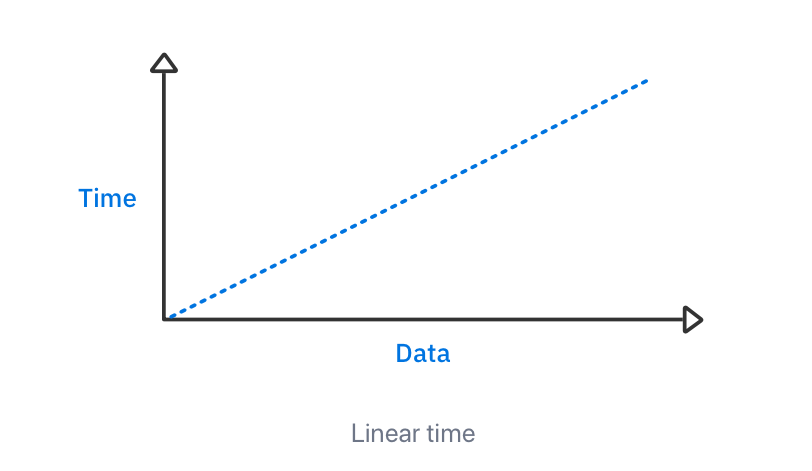
线性时间复杂度通常是最容易理解的。随着数据量的增加，运行时间也会增加相同的量。线性时间的大 O 表示法是 O(n)。

如果一个函数有两个循环外加调用六次 O(1) 方法，时间复杂度是 O(2n + 6) 吗？
时间复杂度仅给出了性能的高级形式，因此发生一定次数的循环并不是时间复杂度的一部分。也即是说，上面的时间复杂度是 O(n) 而非 O(2n + 6) 。
当然，优化绝对效率也很重要。比如，算法的 GPU 优化版本的运行速度可能比原始 CPU 版本快 100 倍，同时保持时间复杂度为 O(n)。虽然在计算时间复杂度时我们会忽略这种优化，但像这样的加速其实也是很重要的。

二次方时间（Quadratic time ）

这种时间复杂度算法，其时间与输入大小的平方成正比。 考虑以下代码：

func printNames(names: [String]) {
  for _ in names {
    for name in names {
      print(name)
    }
  }
}

该函数打印出数组中的所有名称。 如果有一个包含十条数据的数组，它将十次打印十个名称的完整列表，即打印 100 个语句。

如果将输入大小增加 1，它将打印 11 * 11 = 121 个语句。这种增速与之前线性时间运行的函数不同，n squared 算法会随着数据量 n 的增加而呈指数增长。

下图说明了这种行为：

当 n 足够大时，线性增长执行速度远快于指数增长执行速度。

随着输入数据大小的增加，算法运行所需的时间会急剧增加。 因此，n 平方算法在规模上表现不佳。

二次时间的大 O 表示法是 O(n2)。

对数时间（Logarithmic time）

到目前为止，我们已经了解了线性和二次时间复杂度，其中输入的每个元素至少检查一次。 但是，在某些情况下，只需要检查输入的子集，从而加快运行时间。

比如，如果有一个已排序的整数数组，那么查找特定值是否存在捷径呢？

一个笨法是从头到尾逐个检查数组，直到找到要找的值。因为需要检查每个元素一次，时间复杂度为 O(n) 。

线性搜索虽然表现不错，但我们还可以做得更好。由于输入数组已排序，因此我们可以进行如下优化：

let numbers = [1, 3, 56, 66, 68, 80, 99, 105, 450]

func naiveContains(_ value: Int, in array: [Int]) -> Bool {
  for element in array {
    if element == value {
      return true
    }
  }

  return false
}

如果要检查数组中是否存在数字 451，朴素算法从头到尾迭代，对数组中的九个值进行总共九次检查。 但是，由于数组已排序，其实我们可以通过检查中间值立即删除一半没必要的比较：

func naiveContains(_ value: Int, in array: [Int]) -> Bool {
  guard !array.isEmpty else { return false }
  let middleIndex = array.count / 2

  if value <= array[middleIndex] {
    for index in 0...middleIndex {
      if array[index] == value {
        return true
      }
    }
  } else {
    for index in middleIndex..<array.count {
      if array[index] == value {
        return true
      }
    }
  }

  return false
}

上面的函数做了一个小优化，它只需检查数组的一半就能得出结论。

该算法首先检查中间值，如果中间值大于期望值，则直接舍弃中间值以后的部分，因为数组是升序的，期望值只能在中间值之前的那一部分。

同样，如果中间值小于期望值，算法将不会再查看数组的左侧了。

这种二分查找方式，具有对数时间复杂度。下图描述了对数时间算法随输入数据增加时的表现：

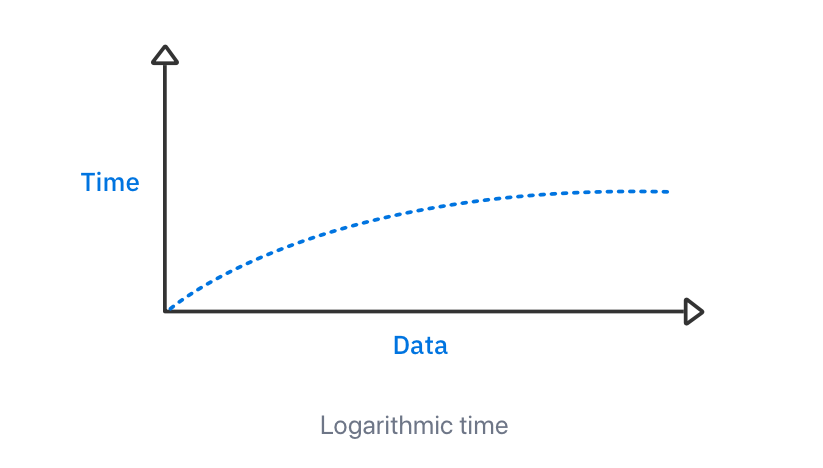
随着输入数据的增加，执行算法所需的时间以缓慢的速度增加。

当输入大小为 100 时，将比较减半意味着可以节省 50 次比较。如果输入大小为 100000，则将比较减半意味着您可以节省 50000 次比较。要比较的的数据越多，减半效应效果越明显。

对数时间复杂度的大 O 表示法是 O(log n)。

拟线性时间（Quasilinear time）

另一个常见时间复杂度是拟线性时间。拟线性时间算法的性能比线性时间差，但比二次时间好得多。它是我们今后将要处理的最常见的算法之一。拟线性时间算法的一个例子是 Swift 的排序方法。

拟线性时间复杂度的 Big-O 表示法是 O(n log n)，它是线性时间和对数时间的乘积。它比线性时间差，但仍比许多其它算法的复杂性好，图表：

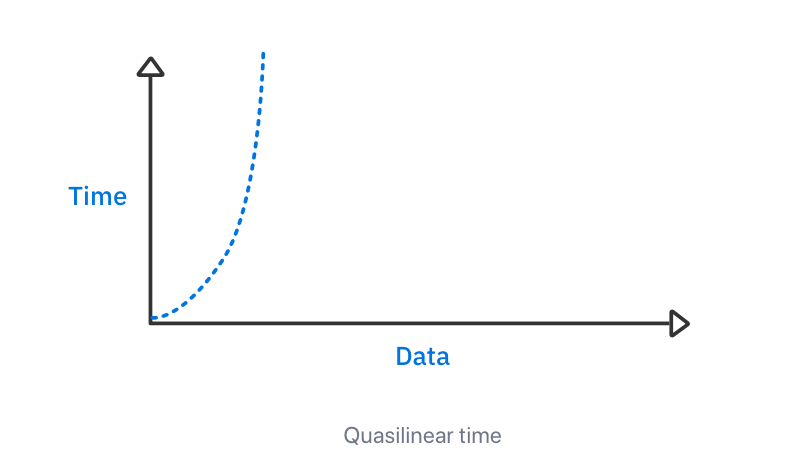
拟线性时间复杂度与二次时间复杂度具有相似的曲线，但上升速度没有那么快，因此对大型数据集更具弹性。

其它时间复杂度

除了上面几种时间复杂度，其它不常见的时间复杂度也存在，比如多项式时间、指数时间、阶乘时间等。

需要注意的是，时间复杂度是对性能的高级概述，它并不能判断算法的速度超出一般的排序方案。这意味着两种算法可以具有相同的时间复杂度，但一种可能仍然比另一种快得多。对于小型数据集，时间复杂度可能不是实际速度的准确度量。

例如，如果数据集很小，则插入排序等二次算法可以比合并排序等拟线性算法更快。这是因为插入排序不需要分配额外的内存来执行算法，而归并排序需要分配多个数组。对于小型数据集，内存分配相对于算法需要接触的元素数量而言可能是更昂贵的。

比较时间复杂度

看以下代码，来查找从 1 到 n 的数字之和：

func sumFromOne(upto n: Int) -> Int {
  var result = 0
  for i in 1...n {
    result += i
  }
  return result
}

sumFromOne(upto: 10000)

代码循环 10000 次并返回 50005000。它是 O(n) 并且需要一点时间才能在 playground 上运行，因为它会计算循环并打印结果。

再看另一个版本：

func sumFromOne(upto n: Int) -> Int {
  (1...n).reduce(0, +)
}
sumFromOne(upto: 10000)

在 Playground 中，这将运行得更快，因为它从标准库中调用已编译的代码。 但是，如果查看 reduce 的时间复杂度，您会发现它也是 O(n)，因为它调用了 + 方法 n 次。它是同一个大 O，但具有更小的常量，因为它是已编译代码（compiled code）。

最后，还可以这样写：

func sumFromOne(upto n: Int) -> Int {
  (n + 1) * n / 2
}
sumFromOne(upto: 10000)

可以使用简单的算术计算总和。该算法的最终版本是 O(1) 并且执行速度很难被击败。

空间复杂度（Space complexity）

算法的时间复杂度可以帮助预测其可扩展性，但它不是唯一的指标。空间复杂度是算法运行所需资源的度量。对于计算机来说，算法的资源就是内存。

我们来看以下代码：

func printSorted(_ array: [Int]) {
  let sorted = array.sorted()
  for element in sorted {
    print(element)
  }
}

上面的 printSorted 方法将创建 array 的排序副本，然后遍历打印该排序数组的值。要计算空间复杂度，需要分析函数的内存分配。

由于 array.sorted() 会产生一个与数组大小相同的全新数组，因此 printSorted 的空间复杂度为 O(n)。尽管此函数简单而优雅，但在某些情况下，我们可能希望分配尽可能少的内存。

因为可以将上述方法优化如下：

func printSorted(_ array: [Int]) {
  // 1
  guard !array.isEmpty else { return }

  // 2
  var currentCount = 0
  var minValue = Int.min

  // 3
  for value in array {
    if value == minValue {
      print(value)
      currentCount += 1
    }
  }

  while currentCount < array.count {

    // 4
    var currentValue = array.max()!

    for value in array {
      if value < currentValue && value > minValue {
        currentValue = value
      }
    }

    // 5
    for value in array {
      if value == currentValue {
        print(value)
        currentCount += 1
      }
    }

    // 6
    minValue = currentValue
  }
}

逐行解释：

1. 检查数组是否为空的情况。如果是，则没有可打印的内容。
2. currentCount 记录打印语句的数量。minValue 存储最后打印的值。
3. 算法首先打印出所有匹配 minValue 的值，并根据打印语句的数量更新 currentCount。
4. 使用 while 循环，算法找到大于 minValue 的最小值并将其存储在 currentValue 中。
5. 然后算法在更新 currentCount 的同时打印数组中 currentValue 的所有值。
6. minValue 设置为 currentValue，下一次迭代将尝试找到下一个最小值。

上述算法只分配内存来跟踪少数变量，因此空间复杂度为 O(1)。这与前面的函数相反，它分配整个数组来创建源数组的排序表示。

其它符号（Other notations）

目前为止，我们已经使用大 O 表示法评估了算法。这是迄今为止程序员评估时最常用的衡量标准。但是，除此还存在其它表示符号。

Big Omega 表示法用于衡量算法的最佳情况运行时间。

Big Theta 表示法用于测量具有相同最佳和最坏情况的算法的运行时间。

本节关键点

时间复杂度是随着输入大小的增加运行算法所需时间的度量。

• 应该了解常数时间、对数时间、线性时间、拟线性时间和二次时间，并能够按成本对其进行排序。
• 空间复杂度是算法运行所需资源的度量。
• 大 O 表示法用于表示时间和空间复杂度的一般形式。
• 时间和空间复杂度是可扩展性的高级度量，他们不测量算法本身的实际速度。
• 对于小型数据集，时间复杂度通常无关紧要。 例如，当 n 很小时，拟线性算法可能比二次算法慢。