顺序存储二叉树

介绍: 顺序存储二叉树,就是将一串数组,以完全二叉树的结构可以前序,中序,后续遍历即可!

小技巧:

数组是从上至下,从左至右一层一层排列的!结点全部靠左,所以是一颗完全二叉树!
假设当前n的下标是4
- 左子结点 = 2n + 1
- 右子结点 = 2n + 2
- 父结点 = (n - 1 ) / 2

如图所示:

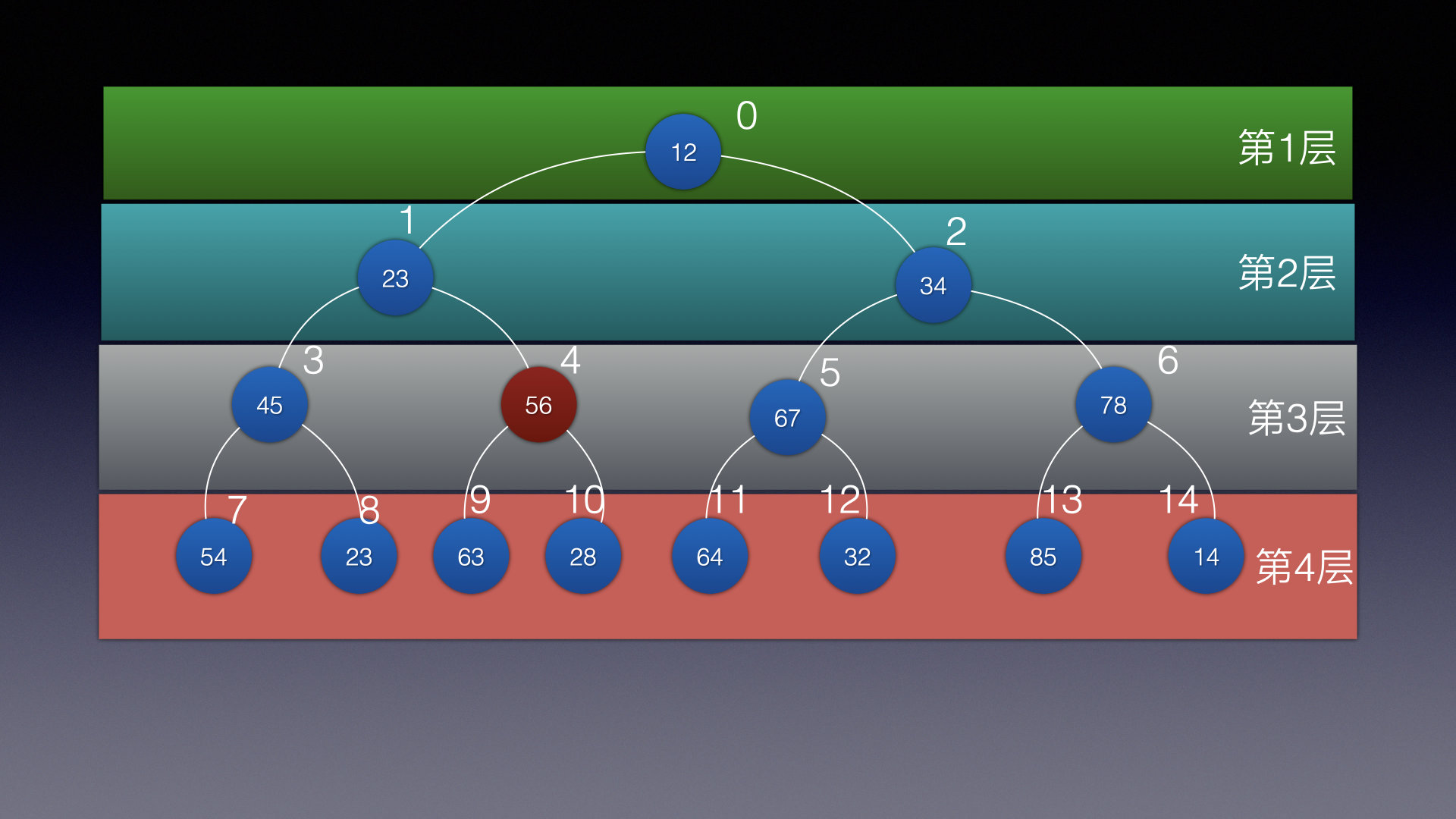
下标n为4的值是45

那么他的左子结点就是 2n + 1, 下标就是9,值是63

那么他的右子结点就是 2n + 2 下标就是10 值是28

那么他的父结点就是 (n - 1 ) / 2 下标就是1 值是23

再来看一张图:

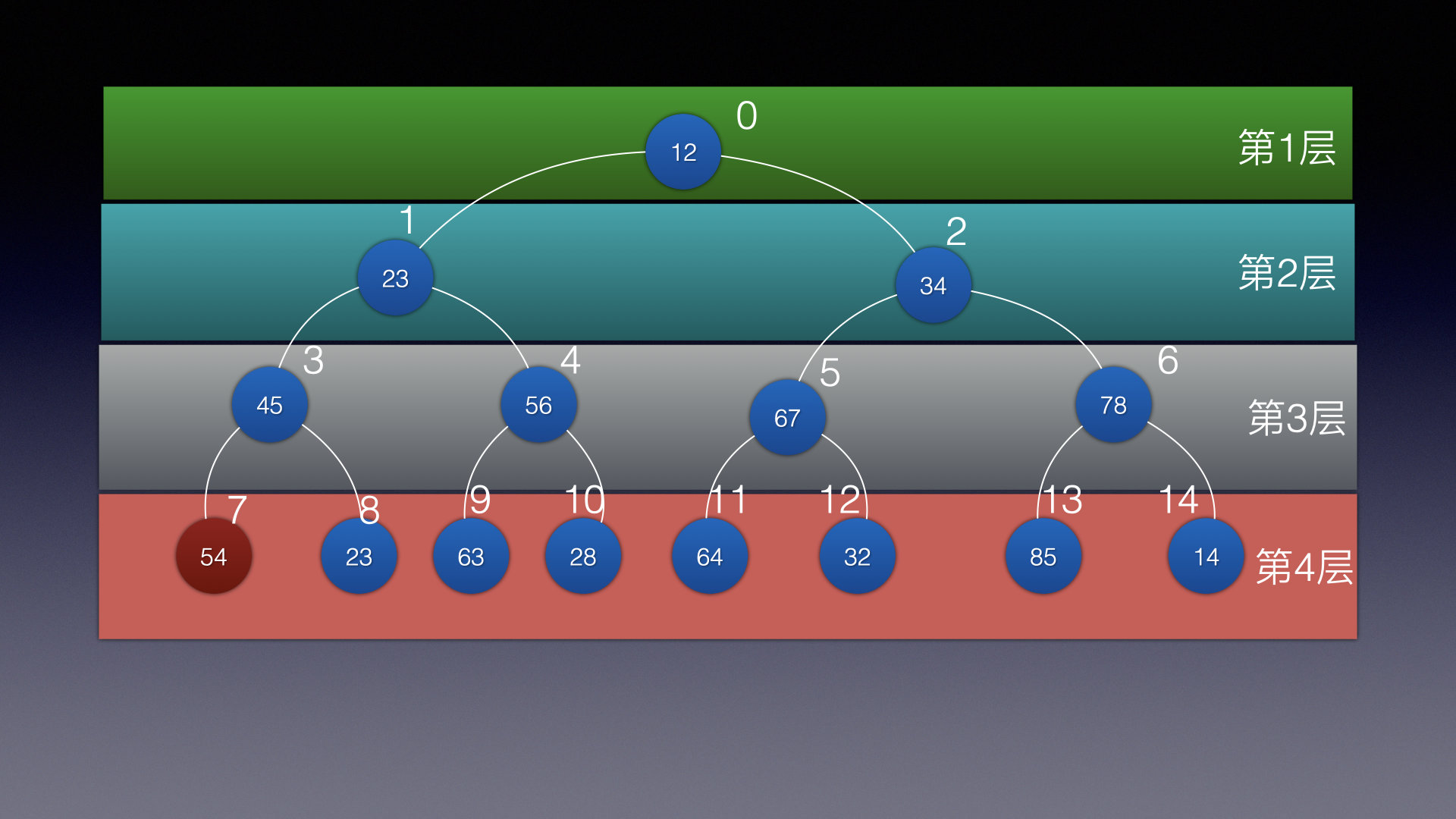
n = 下标

假设当前下标是7

他的左子结点是 2n+1 ,左子结点对应的下标是15 (下标从0开始计算)

现在数组长度是15

所以说没有左子结点

顺序存储二叉树必须是一颗完全二叉树,没有左子结点,他必然没有右子结点,

所以他一定是叶子结点!

现在遍历一颗树的必要条件都满足了:

左子结点 : 2n + 1
右子结点: 2n + 2
父结点: (n-1) / 2
左叶子结点: (2n + 1) < ints.length
右叶子结点: (2n + 2) < ints.length

那么就直接上代码了!

# 前序遍历:
public static void main(String[] args) {
    int[] ints = {666, 3, 5, 12, 4, 23, 8, 53, 123, 34, 285, 83};

    // n = 4
    // n.left = 2n + 1
    //        = 9

    // n.right = 2n + 2
    //         = 10

    // n.parent = (n - 1) / 2
    //          = 3 / 2 = 1

    // 顺序二叉树只考虑完全二叉树
    // 第n个左子节点为 2n + 1
    // 第n个右子节点为 2n + 2
    // 第n个父节点为 (n - 1) / 2
    // n 表示二叉树的第几个元素
    pre(ints, 0);
}

public static void pre(int[] ints, int index) {
    // 前序
    System.out.println(ints[index]);


    int leftIndex = 2 * index + 1;
    // 判断是否是叶子结点
    if (leftIndex < ints.length) {
       // 向左遍历
        pre(ints, leftIndex);
    }

    int rightIndex = 2 * index + 2;
    // 判断是否是叶子结点
    if (rightIndex < ints.length) {
        // 像右遍历
        pre(ints, rightIndex);
    }
}