[数据结构与算法][JavaScript 刷题] 树 - leetcode 235 & 236

[JavaScript 刷题] 树 - leetcode 235 & 236

235. 二叉搜索树的最近公共祖先

github repo 地址: https://github.com/GoldenaArcher/js_leetcode，Github 的目录 大概 会更新的更勤快一些。

题目地址：235. Lowest Common Ancestor of a Binary Search Tree

235 题目

如下：

Given a binary search tree (BST), find the lowest common ancestor (LCA) of two given nodes in the BST.

According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”

235 解题思路

这道题利用二叉搜索树的特性去解：

• 结点的左子树值小于该结点
• 结点的右子树值大于该结点

以案例中的图来说：

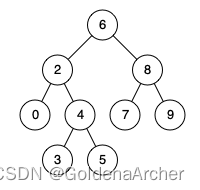
想要找到二叉搜索树的公共节点，只需要找到一个节点满足 $p\le node.val\le q$ 即可，换一个思路就是 $ node.val \nleqq p, q $ 以及 $ node.val \ngeqq p, q $ 即可。

再根据二叉搜索树的特性，如果当前结点小于 $p,q$，则在左数中搜索，反之则在右树中搜索。

使用 JavaScript 解 235

var lowestCommonAncestor = function (root, p, q) {
  if (p.val > root.val && q.val > root.val)
    return lowestCommonAncestor(root.right, p, q);

  if (p.val < root.val && q.val < root.val)
    return lowestCommonAncestor(root.left, p, q);

  return root;
};

236. 二叉树的最近公共祖先

github repo 地址: https://github.com/GoldenaArcher/js_leetcode，Github 的目录 大概 会更新的更勤快一些。

题目地址：236. Lowest Common Ancestor of a Binary Tree

236 题目

如下：

Given a binary tree, find the lowest common ancestor (LCA) of two given nodes in the tree.

According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”

236 解题思路

题目已经给定了说结点一定存在于数种，因此只会存在两种情况：

1. 某结点的左子树和右子树包含对应结点

   

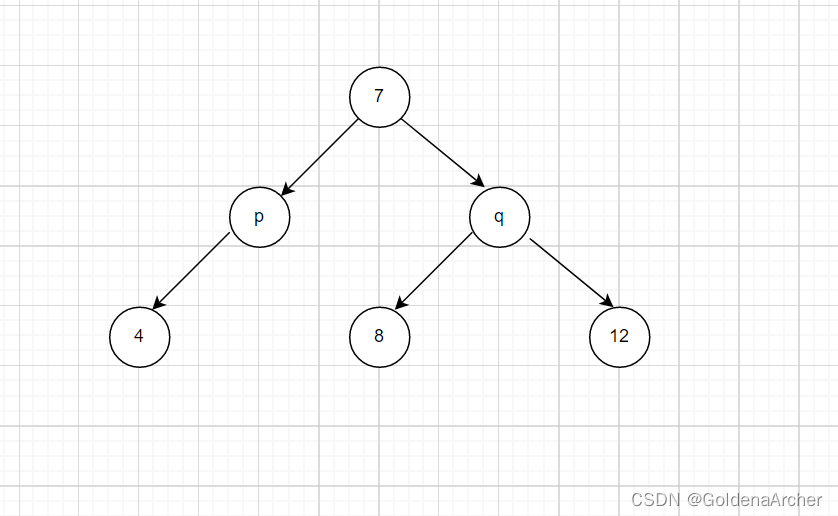
2. 某结点本身为对应结点

   

如果是情况 2 的话，那么直接就可以返回那个 node === p || node === q 这个结点了，因为题目中的两个先提条件：a node to be a descendant of itself 和 p and q will exist in the tree。前者表示一个结点的祖先节点可以是其本身，第二个条件则说明 p 和 q 一定会存在于树中。

使用 JavaScript 解 236

如果 left 和 right 同时存在于当前结点的左子树和右子树，则当前结点为 LCA，否则只要找到返回的结点即可。

var lowestCommonAncestor = function (root, p, q) {
  // base case
  if (!root) return null;

  // 找到对应的结点则进行返回
  if (root === p || root === q) return root;

  const left = lowestCommonAncestor(root.left, p, q);
  const right = lowestCommonAncestor(root.right, p, q);

  return left && right ? root : left || right;
};