题目

给定一个?m x n 二维字符网格?board 和一个字符串单词?word 。如果?word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

示例 1：

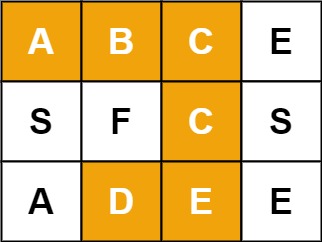
输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出：true
示例 2：

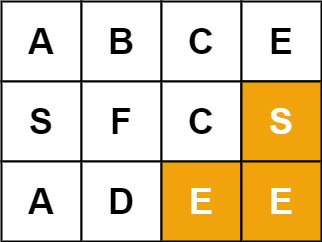
输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"
输出：true
示例 3：

输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"
输出：false
?

提示：

m == board.length
n = board[i].length
1 <= m, n <= 6
1 <= word.length <= 15
board 和 word 仅由大小写英文字母组成

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/word-search
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

因为前不久刚做过一个走迷宫的问题，所以在读完这题后，就发现它与走迷宫惊奇的相似，只不过在走下一步的时候条件有所改变。但是，它还是花了我2个多接近3个小时才写出来的！，唉，不说了，还是我太菜了。

言归正传（菜不能做为我懒惰的理由）

首先，不管是走迷宫还是这一题，都得有一个起点，对于这一题，如果一个一个去试的话，那样就太费时了，所以我首先遍历了整个网格，?找到和要查找的单词的第一个字母一样的字母的位置：
 start_pos_li = []  # 记录单词首字母的位置
        word_set = set()  # 表格中的所有字母
        m, n = len(board), len(board[0])
        for i in range(m):
            for j in range(n):
                word_set.add(board[i][j])
                if board[i][j] == word[0]:
                    start_pos_li.append((i, j))
找到的字母添加到start_pos_li这个列表中，方便以后查找直接从这些位置开始。

同时我也设置了一个集合word_set，保存网格中所有出现的字母，在正式查找之前，可以做一个简单的判断来快速得出一些栗子的答案：
        for s in word:
            if s not in word_set: return False  # 只要有一个字母不在表格中就返回False
如代码所示，遍历需要查找的单词，只要有一个字母不在集合中就直接返回False。

下面就开始正式的查找

?1.首先定义一个移动规则：
 # 移动(四个方向)
    def move(self, x, y, direction):
        if direction == 1:
            return (x - 1, y)
        elif direction == 2:
            return (x + 1, y)
        elif direction == 3:
            return (x, y - 1)
        else:
            return (x, y + 1)
1代表上移，2代表下移，3代表左移，4代表右移；我这里是以横轴作为y轴，纵轴作为x轴，所以上下移动的时候x轴发现变化，左右移动的时候y轴发生变化。

2.开始试探性的走

a.定义一个“栈”来保存走过的路径
path = [start]  # 记录走过的路径
其实这里就是一个列表，但是只使用append()和pop()方法，那么它的行为就像栈。

b.定义一个列表保存每一个格子走过的方向
visit_li = [[set() for j in range(n)] for i in range(m)]  # 记录当前位置到下一步走过的方向
这里每一个格子走过的方向我用的是一个集合来存储的，一个格子最多存储四个方向，即上下左右；与走迷宫不一样的是，在走迷宫中就用来两个值来表示：0代表当前格子没有走过，1代表当前格子已走；因为这里的是一个单词，它要求的是一个连续的序列，当前格子从这个方向过来可能不行，但是从另外一个方向过来就可以。（即从不同的方向取格子，所得到的序列都是不同的）

c.试探+回溯
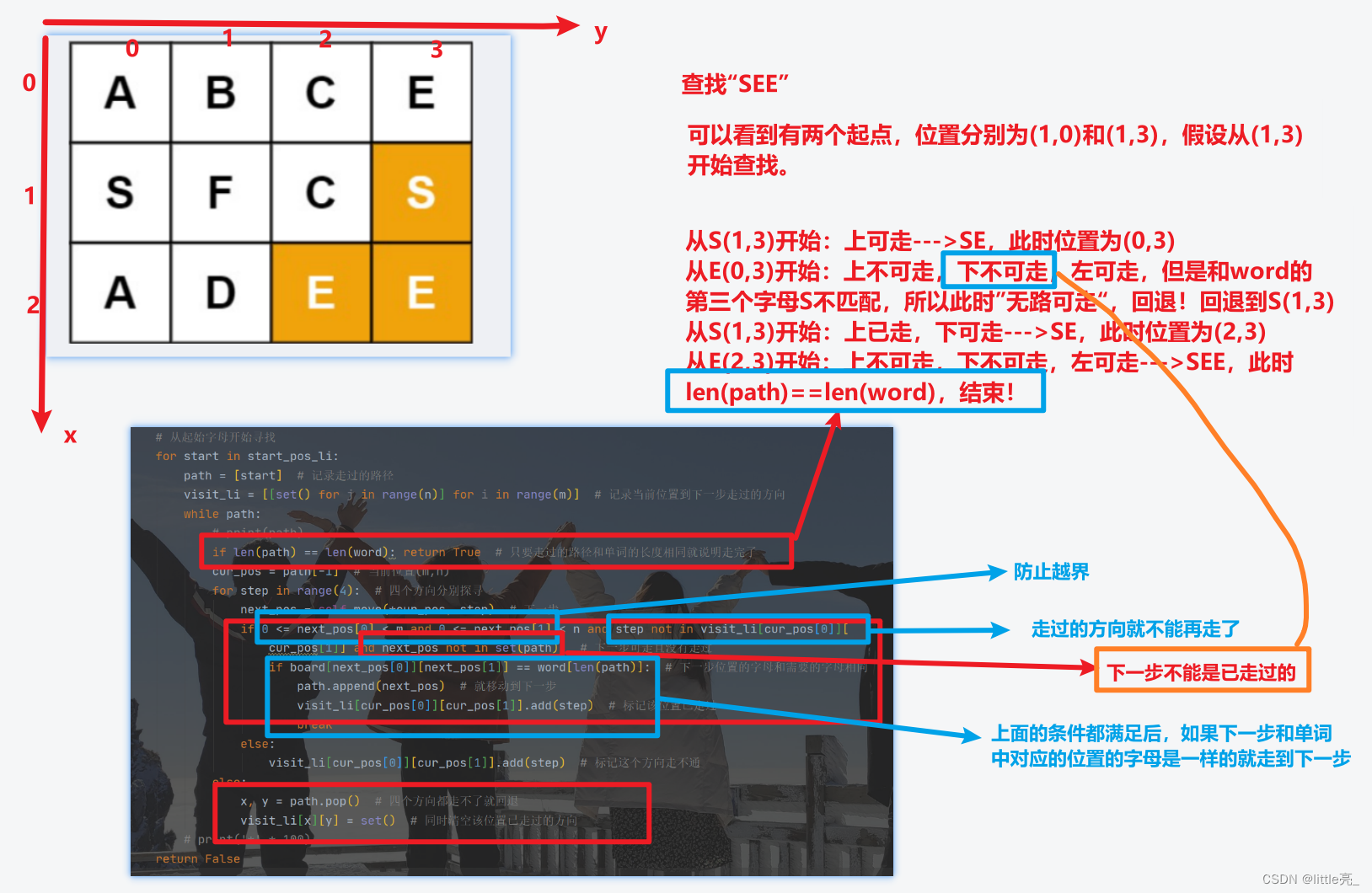
# 从起始字母开始寻找
        for start in start_pos_li:
            path = [start]  # 记录走过的路径
            visit_li = [[set() for j in range(n)] for i in range(m)]  # 记录当前位置到下一步走过的方向
            while path:
                # print(path)
                if len(path) == len(word): return True  # 只要走过的路径和单词的长度相同就说明走完了
                cur_pos = path[-1]  # 当前位置(m,n)
                for step in range(4):  # 四个方向分别探寻
                    next_pos = self.move(*cur_pos, step)  # 下一步
                    if 0 <= next_pos[0] < m and 0 <= next_pos[1] < n and step not in visit_li[cur_pos[0]][
                        cur_pos[1]] and next_pos not in set(path):  # 下一步可走且没有走过
                        if board[next_pos[0]][next_pos[1]] == word[len(path)]:  # 下一步位置的字母和需要的字母相同
                            path.append(next_pos)  # 就移动到下一步
                            visit_li[cur_pos[0]][cur_pos[1]].add(step)  # 标记该位置已走过
                            break
                    else:
                        visit_li[cur_pos[0]][cur_pos[1]].add(step)  # 标记这个方向走不通
                else:
                    x, y = path.pop()  # 四个方向都走不了就回退
                    visit_li[x][y] = set()  # 同时清空该位置已走过的方向
从起点开始，依次试探四个方向是否可走，如果可走更新可走点为当前位置，然后继续试探，如果到某一点，四个方向都行不通，则回溯，退回到上一步；继续上次没有走完的方向，以下面这个栗子为例：

源码

class Solution:
    def exist(self, board: List[List[str]], word: str) -> bool:
        '''
        类似于走迷宫，设置4个移动方向，同时标记走过的地方
        '''

        start_pos_li = []  # 记录单词首字母的位置
        word_set = set()  # 表格中的所有字母
        m, n = len(board), len(board[0])
        for i in range(m):
            for j in range(n):
                word_set.add(board[i][j])
                if board[i][j] == word[0]:
                    start_pos_li.append((i, j))

        for s in word:
            if s not in word_set: return False  # 只要有一个字母不在表格中就返回False

        # 从起始字母开始寻找
        for start in start_pos_li:
            path = [start]  # 记录走过的路径
            visit_li = [[set() for j in range(n)] for i in range(m)]  # 记录当前位置到下一步走过的方向
            while path:
                # print(path)
                if len(path) == len(word): return True  # 只要走过的路径和单词的长度相同就说明走完了
                cur_pos = path[-1]  # 当前位置(m,n)
                for step in range(4):  # 四个方向分别探寻
                    next_pos = self.move(*cur_pos, step)  # 下一步
                    if 0 <= next_pos[0] < m and 0 <= next_pos[1] < n and step not in visit_li[cur_pos[0]][
                        cur_pos[1]] and next_pos not in set(path):  # 下一步可走且没有走过
                        if board[next_pos[0]][next_pos[1]] == word[len(path)]:  # 下一步位置的字母和需要的字母相同
                            path.append(next_pos)  # 就移动到下一步
                            visit_li[cur_pos[0]][cur_pos[1]].add(step)  # 标记该位置已走过
                            break
                    else:
                        visit_li[cur_pos[0]][cur_pos[1]].add(step)  # 标记这个方向走不通
                else:
                    x, y = path.pop()  # 四个方向都走不了就回退
                    visit_li[x][y] = set()  # 同时清空该位置已走过的方向
            # print('*' * 100)
        return False

    # 移动(四个方向)
    def move(self, x, y, direction):
        if direction == 1:
            return (x - 1, y)
        elif direction == 2:
            return (x + 1, y)
        elif direction == 3:
            return (x, y - 1)
        else:
            return (x, y + 1)