? ? ? ? 很常见的搜索算法,问题描述就不必了,直接上解法。
解法一--邻接矩阵--无向图:
????????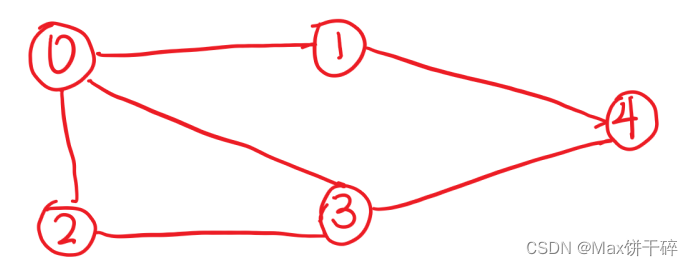
?????????其对应的矩阵为:
????????
? ? ? ? 解法很简单,定义一个队列作为辅助数据类型,visited【】作为访问标志:1为以访问,0为未访问。先把0进队,在队不为空的循环前提下出队0,然后进队与0相连的并且visited为0的节点,重复直至队列为空。
? ? ? ? 数据类型:
typedef struct {
int ed[max][max];
int vexnum, ednum;
}G;? ? ? ? ?代码主体:
void bfs(G g,int *visited) {
queue<int>qu;
qu.push(0);
visited[0] = 1;
while (!qu.empty()) {
int vex = qu.front();
cout << vex << "->";
qu.pop();
for (int i = 0; i < g.vexnum; i++) {
if (g.ed[vex][i] == 1 && visited[i] == 0) {
visited[i] = 1;
qu.push(i);
}
}
}
}解法二--邻接表--有向图:
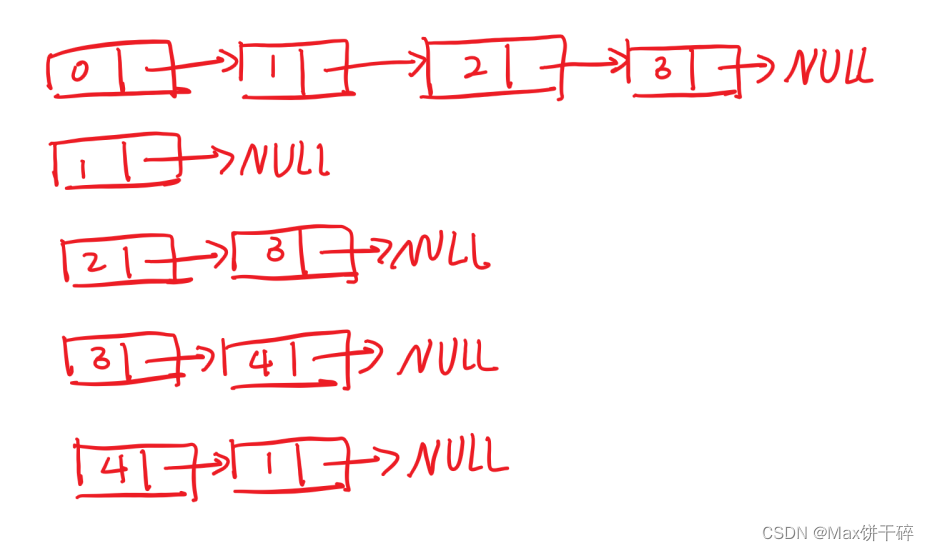
?
?
? ? ? ? 邻接表的广度优先算法跟邻接矩阵其实一样的,只不过矩阵遍历的是二维数组,而邻接矩阵遍历的是链表。
? ? ? ? 数据结构:
typedef struct Vnode {
int vex;
struct Vnode* next;
}VN;
typedef struct Hnode {
int vex;
struct Vnode* first;
}HN;
typedef struct {
HN head[max];
int vexnum, ednum;
}ALG;? ? ? ? 算法主体:
void bfs_alg(ALG g, int* visited) {
queue<int>qu;
qu.push(0);
visited[0] = 1;
while (!qu.empty()) {
int vex = qu.front();
qu.pop();
VN* go = g.head[vex].first;
cout << vex << "->";
while (go != NULL) {
if (visited[go->vex] == 0) {
qu.push(go->vex);
visited[go->vex] = 1;
}
go = go->next;
}
}
}