树型结构
基本概念
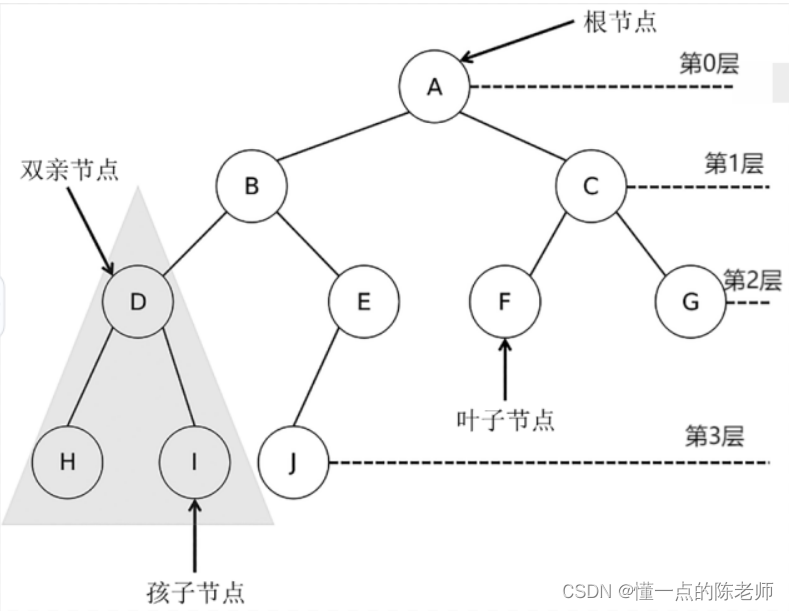
- (1)根节点(Root):树顶端的节点称为根节点,一般一棵树只有一个根节点。
- (2)双亲节点(Parent Node):三角形阴影中的 D 是 H 和 I 的双亲节点。同理,A 是 B 和 C 的双亲节点。
- (3)孩子节点(Child Node):与双亲节点相反,H 和 I 是 D 的孩子节点。
- (4)节点的度(Degree):节点拥有的子树的数目。例如,节点 D 的度为 2,节点 E 的度为 1。
- (5)叶子节点(Leaf Node):度为 0 的节点称为叶子节点。
- (6)兄弟节点( Brother Node):一个双亲节点下的孩子节点互为兄弟节点。例如,H 和 I 为兄弟节点。
- (7)节点层次(Level):根节点为第一层,它的子节点为第二层,依次向下递推,如H、 I、J 均为第四层。
- (8)树的深度(Level of Tree):树中节点的最大层次,如图中树的深度为 3。
- (9)树的度(Degree of Tree):树中节点的度的最大值,如图中树的度为 2。
(1)根节点(Root):树顶端的节点称为根节点,一般一棵树只有一个根节点。
(2)双亲节点(Parent Node):三角形阴影中的 D 是 H 和 I 的双亲节点。同理,A 是 B 和 C 的双亲节点。
(3)孩子节点(Child Node):与双亲节点相反,H 和 I 是 D 的孩子节点。
(4)节点的度(Degree):节点拥有的子树的数目。例如,节点 D 的度为 2,节点 E 的度为 1。
(5)叶子节点(Leaf Node):度为 0 的节点称为叶子节点。
(6)兄弟节点( Brother Node):一个双亲节点下的孩子节点互为兄弟节点。例如,H 和 I 为兄弟节点。
(7)节点层次(Level):根节点为第一层,它的子节点为第二层,依次向下递推,如H、 I、J 均为第四层。
(8)树的深度(Level of Tree):树中节点的最大层次,如图中树的深度为 3。
(9)树的度(Degree of Tree):树中节点的度的最大值,如图中树的度为 2。
二叉树
二叉树(Binary Tree)是一种特殊的树结构,它的每个节点最多有两个子树,也就是树的度不大于2的。
- (1)完美二叉树(Perfect Binary Tree):除了叶子节点之外的每一个节点都有两个孩子节点 , 每一层(包含最后一层)都被完全填充
- (2)完全二叉树(Complete Binary Tree):除了最后一层之外的每一层都被完全填充,并且所有节点都保持向左对齐。
- (3)完满二叉树(Full Binary Tree):除了叶子节点之外的每一个节点都有两个孩子节点。
遍历
-
先序遍历(Pre-order Traversal)是先访问根节点,然后访问左子树,最后访问右子树。访问左子树也是按照这个规则,先访问双亲节点,然后访问左节点,最后访问右节点。
-
中序遍历(In-order Traversal)是从根节点开始,首先访问左子树,然后访问根节点,最后访问右子树。
-
后序遍历(Post-order Traversal)是先访问左子树,然后访问右子树,最后访问根节点。
完整代码实现
# 创建结点对象
class TreeNode(object):
def __init__(self, value, left=None, right=None):
if left is not None and not isinstance(left, TreeNode):
raise ValueError('左孩子结点必须是结点类')
if right is not None and not isinstance(right, TreeNode):
raise ValueError('左孩子结点必须是结点类')
self.value = value # 结点值
self.left = left # 左孩子结点
self.right = right # 右孩子结点
def __repr__(self):
return 'TreeNode({})'.format(self.value)
def insert_left(self,value):
# 在左边插入新的结点
if self.left == None:
self.left = TreeNode(value)
else:
# 若结点存在,把原来结点放到新结点的左孩子结点
tmp = TreeNode(value)
tmp.left = self.left
self.left = tmp
def insert_right(self,value):
# 在右边插入新的结点
if self.right == None:
self.right = TreeNode(value)
else:
# 若结点存在,把原来结点放到新结点的右孩子结点
tmp = TreeNode(value)
tmp.right = self.right
self.right = tmp
def pre_order_traversal(self):
# 先序遍历:根-左-右
result = [self.value] # 先访问根结点
if self.left:
# 再访问左边子树,在子树里面递归使用先序遍历里面的结点
result += self.left.pre_order_traversal()
if self.right:
# 最后访问右边子树
result += self.right.pre_order_traversal()
return result
def in_order_traversal(self):
# 中序遍历:左-根-右
result = []
if self.left:
# 遍历左边子树
result += self.left.in_order_traversal()
# 接着访问根结点
result.append(self.value)
if self.right:
# 遍历右边子树
result += self.right.in_order_traversal()
return result
def post_order_traversal(self):
# 后序遍历:左-右-根
result = []
if self.left:
result += self.left.post_order_traversal()
if self.right:
result += self.right.post_order_traversal()
result.append(self.value)
return result
运行结果
# 创建二叉树例子
binary_tree = TreeNode('A')
binary_tree.insert_left('B')
binary_tree.insert_right('C')
binary_tree.left.insert_left('D')
binary_tree.left.insert_right('E')
binary_tree.right.insert_left('F')
binary_tree.right.insert_right('G')
# 根据三种遍历方式,访问二叉树的数据
res = binary_tree.pre_order_traversal()
print("先序遍历", "->".join(res))
res = binary_tree.in_order_traversal()
print("中序遍历", "->".join(res))
res = binary_tree.post_order_traversal()
print("后序遍历", "->".join(res))
先序遍历 A->B->D->E->C->F->G
中序遍历 D->B->E->A->F->C->G
后序遍历 D->E->B->F->G->C->A
练习:判断是否为完美二叉树
def if_perfect(tree):
# 根据完美二叉树定义,它的叶子数量=2^(树的深度-1)
max_depth = 0 # 树最大的深度
leaf_count = 0 # 叶子数量
size = 0 # 结点数量
current_nodes = [tree]
while len(current_nodes) > 0:
max_depth += 1
next_nodes = []
for node in current_nodes:
size += 1
if node.left is None and node.right is None:
leaf_count += 1 # 根据定义,没有孩子结点就是叶子结点
if node.left is not None:
next_nodes.append(node.left)
if node.right is not None:
next_nodes.append(node.right)
current_nodes = next_nodes
print("叶子的深度{},叶子数量{},因此它{}完美二叉树".format(
max_depth,leaf_count,
"是" if leaf_count == 2 ** (max_depth-1) else "不是"))