[数据结构与算法]回文子串、回文子序列问题

409. 最长回文串 ●

描述

给定一个包含大写字母和小写字母的字符串 s ，返回 通过这些字母构造成的 最长的回文串 。

在构造过程中，请注意 区分大小写 。比如 “Aa” 不能当做一个回文字符串。

示例

输入:
s = “abccccdd”
输出:
7
解释:
我们可以构造的最长的回文串是"dccaccd", 它的长度是 7。

题解

1. 贪心 + 哈希表

哈希表记录每个字母出现的个数，如果是双数，答案就加本身，如果是单数，答案就加本身减一，并且可以放一个字母在字符串正中间，所以最后答案加一。

• 时间复杂度：$O(N)$，其中 N 为字符串 s 的长度。我们需要遍历每个字符一次。
• 空间复杂度：$O(S)$，其中 S 为字符集大小。题目中保证了给定的字符串 s 只包含大小写字母，因此我们也可以使用哈希映射（HashMap）来存储每个字符出现的次数，例如 Python 和 C++ 的代码。如果使用哈希映射，最多只会存储 52 个（即小写字母与大写字母的数量之和）键值对。

class Solution {
public:
    int longestPalindrome(string str) {
        int ans = 0, flag = 0;
        unordered_map<char, int> hash;
        for(char ch : str){
            ++hash[ch];         // 统计字母出现次数
        }
        for(auto pairs : hash){
            if(flag == 0 && pairs.second % 2 != 0){
                flag = 1;       // 奇数个数，可以有一个字母位于正中间
            }
            ans += pairs.second % 2 == 0? pairs.second : pairs.second-1;    // 偶数个数为本身，奇数个数为本身-1
        }
        ans += flag;            // 加上正中间的字母数
        return ans;
    }   
};

5. 最长回文子串 ●●

给你一个字符串 s，找到 s 中最长的回文子串。
–
输入：s = “babad”
输出：“bab”
解释：“aba” 同样是符合题意的答案。

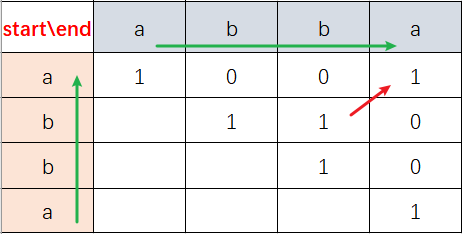
动态规划思路与647. 回文子串 ●●类似；

1. dp[i][j] 表示 [i, j] 范围内的子串是否为回文串
2. 遍历过程有三种情况，当长度为最大时更新返回字符串 ans；
   1）只有一个字符，属于回文串
   2）s[i] != s[j]，非回文串
   3）s[i] == s[j]，判断中间部分 [i+1, j-1] 是否为回文串（只有两个字符时单独讨论）
3. dp 初始化为 false
4. dp[i][j] 可能要根据 dp[i+1, j-1] 进行判断，因此外层起始位置 i 从后往前遍历，内层终止位置 j 从前往后遍历

时间复杂度：$O(n^2)$
空间复杂度：$O(n^2)$

class Solution {
public:
    string longestPalindrome(string s) {
        int len = s.length();
        vector<vector<bool>> dp(len, vector<bool>(len, false));
        int maxL = 1;
        string ans(1, s[0]);
        for(int i = len-1; i >= 0; --i){    // 外层从后往前遍历
            dp[i][i] = true;                // 单个字符
            for(int j = i+1; j < len; ++j){ // 内层从前往后
                if(s[i] == s[j]){           
                    if(j - i == 1){         // 两个字符
                        dp[i][j] = true;
                        if(maxL < 2){       // 判断长度
                            maxL = 2;
                            ans = string(s.begin() + i, s.begin() + j + 1);
                        }
                    }else if(dp[i+1][j-1]){ // 3个字符及以上，判断中间部分
                        dp[i][j] = true;
                        if(maxL < j - i + 1){   // 判断长度
                            maxL = j - i + 1;
                            ans = string(s.begin() + i, s.begin() + j + 1);
                        }
                    }
                }
            }
        }
        return ans;
    }
};

647. 回文子串 ●●

给你一个字符串 s ，请你统计并返回这个字符串中 回文子串 的数目。
回文字符串 是正着读和倒过来读一样的字符串。
子字符串 是字符串中的由连续字符组成的一个序列。
具有不同开始位置或结束位置的子串，即使是由相同的字符组成，也会被视作不同的子串。
–
输入：s = “aaa”
输出：6
解释：6个回文子串: “a”, “a”, “a”, “aa”, “aa”, “aaa”

1. 暴力遍历

两层 for 循环，遍历区间起始位置和终止位置，然后判断这个区间是不是回文。

时间复杂度：$O(n^3)$

class Solution {
public:
    bool isValid(string s, int start, int end){     // 回文字符串 判断
        for(int i = 0; i <= (end - start) / 2; ++i){
            if(s[start + i] != s[end-i]) return false;
        }
        return true;
    }
    
    int countSubstrings(string s) {
        int len = s.length();
        int ans = 0;
        for(int i = 0; i < len; ++i){           // 以s[i]开头的字符串判断
            ++ans;
            for(int j = i+1; j < len; ++j){     // 遍历到末尾
                if(isValid(s, i, j)) ++ans;     // 回文子串判断
            }
        }
        return ans;
    }
};

2. DP

1. dp[i][j] 表示 [i, j] 范围内的子串是否为回文串
2. 遍历过程有三种情况：
   1）只有一个字符，属于回文串
   2）s[i] != s[j]，非回文串
   3）s[i] == s[j]，判断中间部分 [i+1, j-1] 是否为回文串（只有两个字符时单独讨论）
3. dp 初始化为 false
4. dp[i][j] 可能要根据 dp[i+1, j-1] 进行判断，因此外层起始位置 i 从后往前遍历，内层终止位置 j 从前往后遍历

时间复杂度：$O(n^2)$
空间复杂度：$O(n^2)$

class Solution {
public:
    int countSubstrings(string s) {
        int len = s.length();
        int ans = 0;
        vector<vector<bool>> dp(len, vector<bool>(len, false)); // dp[i][j] 表示[i, j]范围内的子串是回文串
        for(int i = len-1; i >= 0; --i){        // 起始位置 从后往前遍历
            dp[i][i] = true;        // 单个字符
            ++ans;
            for(int j = i+1; j < len; ++j){     // 结束位置 从前往后遍历
                if(s[i] == s[j]){               // 首尾相等的前提下
                    if(j - i == 1){
                        dp[i][j] = true;        // 2个字符，回文
                        ++ans;
                    }else if(dp[i+1][j-1]){     // 3个字符及以上，判断中间是否回文
                        dp[i][j] = true;
                        ++ans;
                    }
                }   // 其余情况则非回文，不操作
            }
        }
        return ans;
    }
};

3. 双指针（中心扩展）

枚举所有的中心点，然后用两个指针分别向左右两边拓展，当两个指针指向的元素相同的时候就拓展，否则停止拓展。

对一个字符串 ababa，选择最中间的 a 作为中心点，往两边扩散，第一次扩散发现 left 指向的是 b，right 指向的也是 b，所以是回文串，继续扩散，同理 ababa 也是回文串。

如何有序地枚举所有可能的回文中心，我们需要考虑回文长度是奇数和回文长度是偶数的两种情况。如果回文长度是奇数，那么回文中心是一个字符；如果回文长度是偶数，那么中心是两个字符;所以最终的中心点有 2 * len - 1 个，分别是 len 个单字符和 len - 1 个双字符。

• 时间复杂度：$O(n^2)$，枚举回文中心的是 $O(n)$ 的，对于每个回文中心拓展的次数也是 $O(n)$。
• 空间复杂度：$O(1)$

单个字符和两个字符单独计算：

class Solution {
public:
    int countSubstrings(string s) {
        int ans = 0;
        for(int i = 0; i < s.length(); ++i){
            ans += centerCount(s, i, i);	// 单个字符为中心
            ans += centerCount(s, i, i+1);	// 两个字符为中心
        }        
        return ans;
    }

    int centerCount(string s, int left, int right){      // 中心扩展
        int ans = 0;
        while(left >= 0 && right < s.length() && s[left] == s[right]){
            --left;		// 两边扩展
            ++right;
            ++ans;		// 个数 + 1 
        }
        return ans;
    }
};

字符串中心合并计算：

遍历2 * len - 1个中心点，left = i / 2；right = left + i %2；

class Solution {
public:
    int countSubstrings(string s) {
        int ans = 0;
        for(int i = 0; i < 2 * s.length() + 1; ++i){	// 遍历2 * len - 1个中心点
            int left = i / 2;
            int right = left + i % 2;
            while(left >= 0 && right < s.length() && s[left] == s[right]){
                --left;
                ++right;
                ++ans;
            }
        }        
        return ans;
    }
};

4. Manacher 算法

• 时间复杂度：O(n)
• 空间复杂度：O(n)

HJ85 最长回文子串 ●

描述

给定一个仅包含小写字母的字符串，求它的最长回文子串的长度。

所谓回文串，指左右对称的字符串。
所谓子串，指一个字符串删掉其部分前缀和后缀（也可以不删）的字符串

数据范围：字符串长度$1\le s\le 350$

进阶：时间复杂度：O(n)\O(n) ，空间复杂度：O(n)\O(n)

示例

输入:
cdabbacc
输出:
4
解释:
abba为最长的回文子串

题解

ACM 模式（中心扩散 & 动态规划）

#include <iostream>
#include <string>
#include <vector>
#include <algorithm>
using namespace std;

int from_center(string &str, int start, int end){
    if(str[start] != str[end]){
        return 1;
    }
    int ans = end - start + 1;          // 判断中心长度
    int l = start - 1, r = end + 1;     // 中心扩展
    while(l >= 0 && r < str.length()){
        if(str[l--] != str[r++]) break;
        ans += 2;
    }
    return ans;
}

int main(){
    string str;
    while(cin >> str){
        int ans = 1, n = str.length();

        // =========== from_center ===========
        // for(int i = 0 ; i < str.length()-1; ++i){
        //     ans = max(ans, from_center(str, i, i));     // 一个字母为中心
        //     ans = max(ans, from_center(str, i, i+1));   // 两个字母为中心
        // }


        // =============== DP ================
        vector<vector<bool>> dp(n, vector<bool>(n, false));	// dp[i][j] 表示｛i,j｝范围内的字符串是否回文
        for(int i = n-1; i >= 0; --i){
            dp[i][i] = true;					// 单个字母，回文
            for(int j = i+1; j < n; ++j){
                if(str[i] != str[j]) break;		// 首尾是否相同
                int len = j-i+1;
                if(len == 2){					// 长度为2，直接判断回文
                    dp[i][j] = true;
                    ans = max(ans, len);
                }else if(dp[i+1][j-1]){			// 长度大于2，判断中间部分是否回文
                    dp[i][j] = true;
                    ans = max(ans, len);
                }
            }
        }

        cout << ans << endl;
    }
    return 0;
}

516. 最长回文子序列 ●●

给你一个字符串 s ，找出其中最长的回文子序列，并返回该序列的长度。
子序列定义为：不改变剩余字符顺序的情况下，删除某些字符或者不删除任何字符形成的一个序列。
–
输入：s = “bbbab”
输出：4
解释：一个可能的最长回文子序列为 “bbbb” 。

回文子串是要连续的，回文子序列可不是连续的！

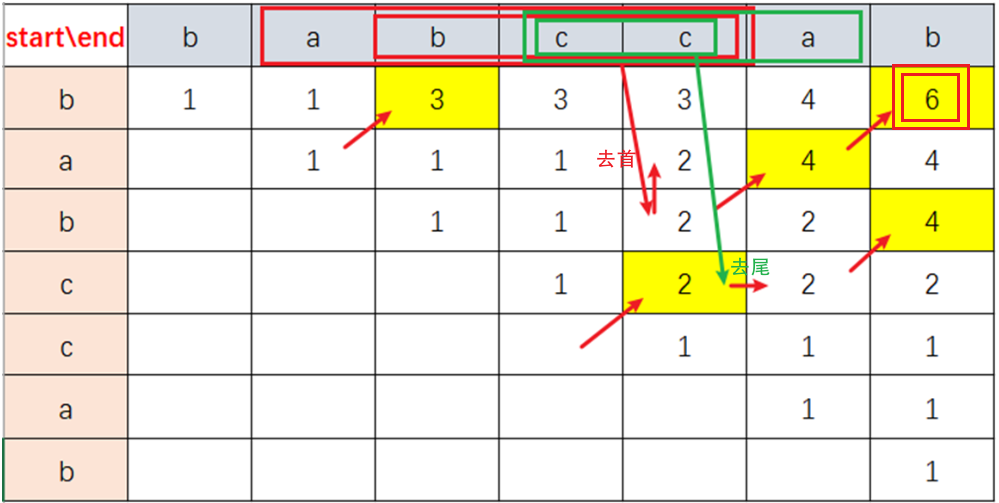
1. dp[i][j] 表示 [i, j] 范围内的子串中最长回文子序列数
2. 遍历过程有两种情况：
   1）s[i] == s[j]，则中间部分 [i+1, j-1] 回文子序列长度 + 2
   dp[i][j] = dp[i+1][j-1] + 2;
   2）s[i] != s[j]，选择 去首 或 去尾 的子串中最长的回文子序列长度。
   dp[i][j] = max(dp[i+1][j], dp[i][j-1]);
3. dp 初始化为 0，dp[i][i] 为 1
4. dp[i][j] 可能要根据 dp[i+1, j-1] 进行判断，因此外层起始位置 i 从后往前遍历，内层终止位置 j 从前往后遍历

时间复杂度：$O(n^2)$
空间复杂度：$O(n^2)$

class Solution {
public:
    int longestPalindromeSubseq(string s) {
        int len = s.length();
        vector<vector<int>> dp(len, vector<int>(len, 0));
        for(int i = len - 1; i >= 0; --i){	// 外层起始位置 i 从后往前遍历
            dp[i][i] = 1;
            for(int j = i+1; j < len; ++j){	// 内层终止位置 j 从前往后遍历
                if(s[i] == s[j]){
                    dp[i][j] = dp[i+1][j-1] + 2;	// 去掉首尾的回文子序列长度 + 1
                }else{
                    dp[i][j] = max(dp[i+1][j], dp[i][j-1]);	// 选择 去首 或 去尾
                }
            }
        }
        return dp[0][len-1];	// 范围整个字符串范围内的最长子序列长度
    }
};