????????学完数据结构已经有好长一段时间了,最近又重新回顾,做一个八大排序的总结,以便后期回顾。
目录
一、插入排序
1.直接插入排序
? ? ? ?直接插入排序,简单的来说就是依次将后面一个元素和前面所有的元素作比较,然后选择合适的位置插入,直接插入排序稳定性好。下面是代码示例。
void InsertSort(int *a, int len)
{
int i, j, tmp;
for(i = 1; i < len-1; i++)
{
a[i] = tmp;
for(j = i-1; j >= 0; j--)
{
if(tmp < a[j]) //决定排序的顺序为递增或递减,tmp在前递增,tmp在后递减
{
a[j++] = a[j];
}
else
{
break;
}
}
a[j++] = tmp;
}
}2.希尔排序
? ? ? ? 希尔排序,定义一个增量h = length /2,以增量h为间隔进行插入排序,然后将增量h/2再次进行直接插入排序,最后进行增量为1的直接插入排序,此时应该基本有序。
? ? ? ? 简单来说就是进行分组,分组后进行直插排序。个人理解如下:在直插排序的基础上进行,是插入排序的一种更高效的改进版本。但是希尔排序不稳定,在使用时要根据情况进行选择。3
void ShellSort(int *a, int len)
{
int i, j, tmp, h;
for(h = len / 2; h > 0; h /= 2)
{
for(i = h; i < len; i++)
{
a[i] = tmp;
for(j = i - h; j >= 0; j -= h)
{
if(tmp < a[j])
{
a[j + h] = a[j];
}
else
{
break;
}
}
a[j + h] = tmp;
}
}
}?二、交换排序
1.冒泡排序
? ? ? ? 冒泡排序,应该是在学c语言时接触最早的排序方法,简单来说就是通过依次将前面一个元素和后面所有的元素作比较,然后按照大小进行交换得到想要的顺序。冒泡排序比较稳定。
void BubbleSort(int *a, int len)
{
int i, j, tmp;
for(i = 0; i < len - 1; i++)
{
for(j = i + 1; j < len; j++)
{
if(a[i] > a[j])
{
tmp = a[i];
a[i] = a[j];
a[j] = tmp;
}
else
{
break;
}
}
}
}2.快速排序
? ? ? ? 快速排序,通过一趟排序将待排序的序列分割成两个独立的部分,其中一部分记录的数字都比关键字小,另一部分都比关键字大,然后再对这两个部分继续进行排序, 以达到整体有序的目的。
void QuickSort(int *a, int start, int end)
{
if(start > end)
{
return;
}
int x, y, base;
x = start;
y = end;
base = a[start];
while(x < y)
{
while(a[y] > base && x < y)
{
y--;
}
if(x < y)
{
a[x++] = a[y];
}
while(a[x] > base && x < y)
{
x++;
}
if(x < y)
{
a[y--] = a[x];
}
}
a[x] = base;
QuickSort(a, start, x - 1);
QuickSort(a, x + 1, end);
}三、选择排序
1.简单选择排序
? ? ? ? 简单选择排序,就是通过n-i关键词的比较,从n-i-1中选出关键词最小的记录,并和第i个记录交换之。
void SelectSort(int *a, int len)
{
int i, j, tmp, index;
for(i = 0; i < len; i++)
{
index = i;
tmp = a[i];
for(j = i + 1; j < len; j++)
{
if(a[j] < tmp)
{
tmp = a[j];
index = j;
}
}
if(i != index)
{
index = i;
a[i] = tmp;
}
}
}2.堆排序
? ? ? ? 堆排序,将待排序列构造成一个大顶堆,此时,整个序列的最大值就是堆顶的根节点,然后将其和某位元素进行交换,然后将除了最后一个元素外的所有元素重新构造成一个堆,这样就会得到n个元素 的次大值,如此反复执行,就可以得到一个有序的序列。
? ? ? ? 在这里要提前说一下,在写堆排序时要对二叉树的结构有一定的了解,了解树的特点才能写好代码,例如什么是左子树、什么是右子树、父结点和孩子结点之间的关系等等有大致的了解。在这先列出几个二叉树的性质:
????????性质1:在二叉树的第i层至多有2^(i -1)个结点。
????????性质2:深度为K的二叉树最多有2^k - 1个结点。
????????性质3:对任何一个二叉树,如果其终端结点数为n,度为2的结点数为m,则:n = m+1;
????????性质4:具有n个结点的完全二叉树,其深度为(log2n)+1或『log2(n+1)。
????????性质5:如果对1棵有n个结点的二叉树的结点按层序编号,对任何一个结点i
????????(1)如果i= 1,则结点i是二叉树的根,无双亲,如果,如果i > 1,则其双亲结点为 i/2 。
????????(2)如果2i > n,则结点无左孩子,否则,其左孩子为2i。
????????(3)如果2i+ 1 > n,则结点无右孩子,否则,其右孩子为2i+1。
? ? ? ? 回归正题,简单来说堆排序就是通过父结点和孩子结点的比较,通过比较将整个树中最大的结点通过移动到或者交换到树的根结点(顶端),构成大顶堆。(小顶堆与之相反,根据具体需要可自行选择)在构成大顶堆之后,将堆顶的根结点与最后一个叶子结点进行交换,下一次进行排序时去除掉最后的叶子结点,如此循环每次去除掉的叶子结点的值即为排序后的值。参考代码再理解一下吧。
void AdjustHeapSort(int *a, int root, int last)
{
int child, tmp = a[root];
for(; 2 * root + 1 <= last; root = child) //注意:这里的root = child 在进行叶子节点和其父结点的比较和交换时不会有什么作用,当进行到非叶子结点与其父结点进行比较和交换时,需要做到交换后的结点其子结点中再无比该结点值大的结点,如若有其子结点的值大于交换后该结点值的,则需要再往下走再做交换,此时root = child的作用就会体现出来。
{
child = 2 * root + 1;
if(child + 1 <= last && a[child] < a[child + 1])
{
child++;
}
if(a[child] > a[root])
{
a[root] = a[child];
a[child] = tmp;
}
}
}
void Swap(int *a, int *b)
{
int tmp = int *a;
*a = *b;
*b = tmp;
}
void HeapSort(int *a, int len)
{
int i;
//构建大顶堆,i为数组下标
for(i = len / 2 -1; i >= 0; i--)
{
AdjustHeapSort(a, i, len-1);
}
//进行交换和再次排序
for(i = len - 1; i > 0; i--)
{
Swap(&a[0], &a[i]); //交换根结点和最后一个叶子结点的值
AdjustHeapSort(a, 0, i-1); //去掉最后一个叶子结点,重新进行构建大顶堆
}
}四、归并排序
? ? ? ? 归并排序,先将长度为m的序列进行拆分,拆成单独的子序列,然后再两两进行归并,如此重复,最后得到一个有序序列,这种排序称为2路归并排序。相比堆排序,这个的思路就很清晰,捋一遍代码基本就能理解。????
void Merge(int *a, int start, int mid, int end)
{
//左右俩边长度
int Left_len = mid - start + 1;
int Right_len = end - mid;
//给左右俩部分分配空间
int * L = (int *)malloc(sizeof(int) * Left_len);
int * R = (int *)malloc(sizeof(int) * Right_len);
int i, j, k;
//给左边部分赋值
for(i = 0, k = start; i < Left_len; i++, k++)
{
L[i] = a[k];
}
//给右边部分赋值
for(j = 0; j < Right_len; j++, k++)
{
R[j] = a[k];
}
//左右部分进行对比,小的值先放进原数组
for(i = 0, j = 0, k = start; i < Left_len && j < Right_len; k++)
{
if(L[i] < R[j])
{
a[k] = L[i++];
}
else
{
a[k] = R[j++];
}
}
//当右半部分先放完时
if(i < Left_len)
{
for(; i < Left_len; i++, k++)
{
a[k] = L[i];
}
}
//当左半部分先放完时
if(j < Right_len)
{
for(; j < Right_len; j++, k++)
{
a[k] = R[j];
}
}
//手动清除申请的空间并置空
free(L);
free(R);
L = NULL;
R = NULL;
}
void MergeSort(int *a, int start, int end)
{
if(start >= end)
{
return;
}
//找到中间值,然后进行拆分
int mid = (start + end) / 2;
MergeSort(a, 0, mid);
MergeSort(a, mid + 1, end);
//合并
Merge(a, start, mid, end);
}五、基数排序(桶排序)
? ? ? ? 基数排序,从低位开始将待排序的数按照这一位的值放到相应的编号为0-9的桶种,等到低位 排完得到一个子序列,再将这个序列按照次低位的大小进入相应的桶中,一直排到最高位位置, 数组排序完成。给个图例更加清晰。
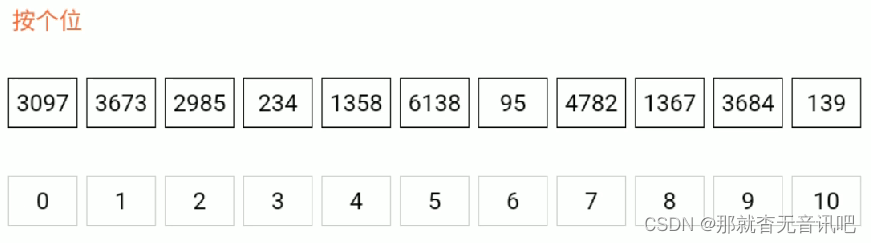
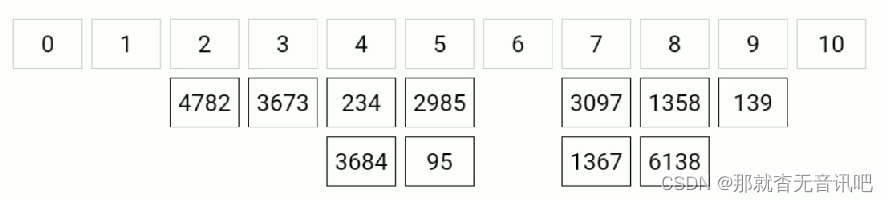

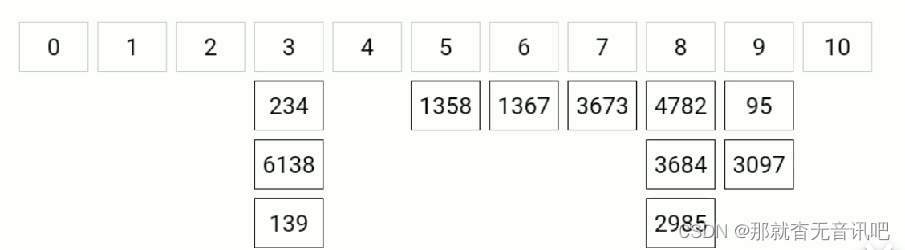 ?
?

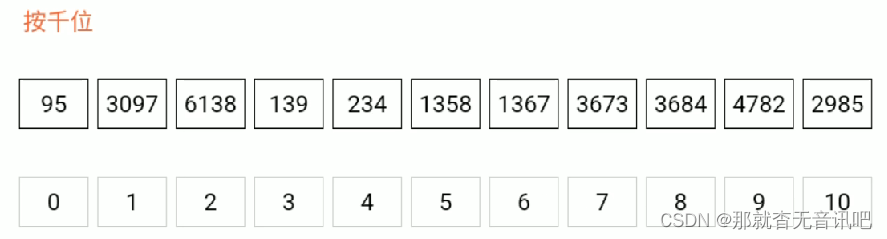
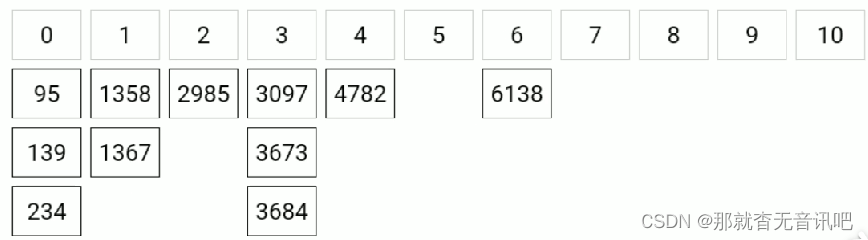

?代码和图方式有差异,图是为了理解何为基数排序,代码需要思考:
//方法一
void RadixSort(int *a,int length)
{
int i,max =a[0],base = 1;
for(i = 1; i < length;i++)
{
if(a[i] > max)
{
max = a[i];
}
}
int *t = (int *)malloc(sizeof(int)*length);
while(max / base > 0)
{
int bucket[10] = {0};
for(i = 0 ; i < length;i++)
{
bucket[a[i] / base % 10]++;
}
for(i = 1; i < 10;i++)
{
bucket[i] += bucket[i -1];
}
for(i = length -1; i >=0;i--)
{
t[bucket[a[i] /base % 10] -1] = a[i];
//同一个位置出现多个数字的时候,要往前挪
bucket[a[i]/base %10]--;
}
for(i = 0 ; i < length;i++)
{
a[i] = t[i];
}
base = base *10;
}
}
//方法二
void RadixSort(int *a,int length)
{
int max = a[0];
int bucket[10][length];
int base = 1;
int buckeIndex[10] = {0};
//找出最大值
for(int i = 0; i < length; i++)
{
max = a[i] > max ? a[i] : max;
}
//循环最大值的位数
while(max / base > 0)
{
for(int i = 0; i < length; i++)
{
//求出个位、十位、百位、千位
int tmp = a[i] / base % 10;
//tmp bucket[tmp] 第tmp个下标所在的一维数组
//buckeIndex[tmp]对应下标桶
bucket[tmp][buckeIndex[tmp]++] = a[i];
//buckeIndex[tmp]++;
}
//把桶中数据重新赋值给原始数组
int index = 0;
for(int i = 0; i < 10; i++)
{
if(buckeIndex[i] != 0)
{
for(int j = 0; j < buckeIndex[i]; j++)
{
a[index++] = bucket[i][j];
}
}
}
//清空下标桶
memset(buckeIndex, 0, sizeof(buckeIndex));
base *= 10;
}
}