[数据结构与算法]PTA数据结构专项练习

8.0-1背包问题
7.最长有序子序列
6.铺满方格
5.计算n!(n要能大于13）
3.八皇后问题
2.哈夫曼编码
1.愿天下有情人都是失散多年的兄妹

8.0-1背包问题

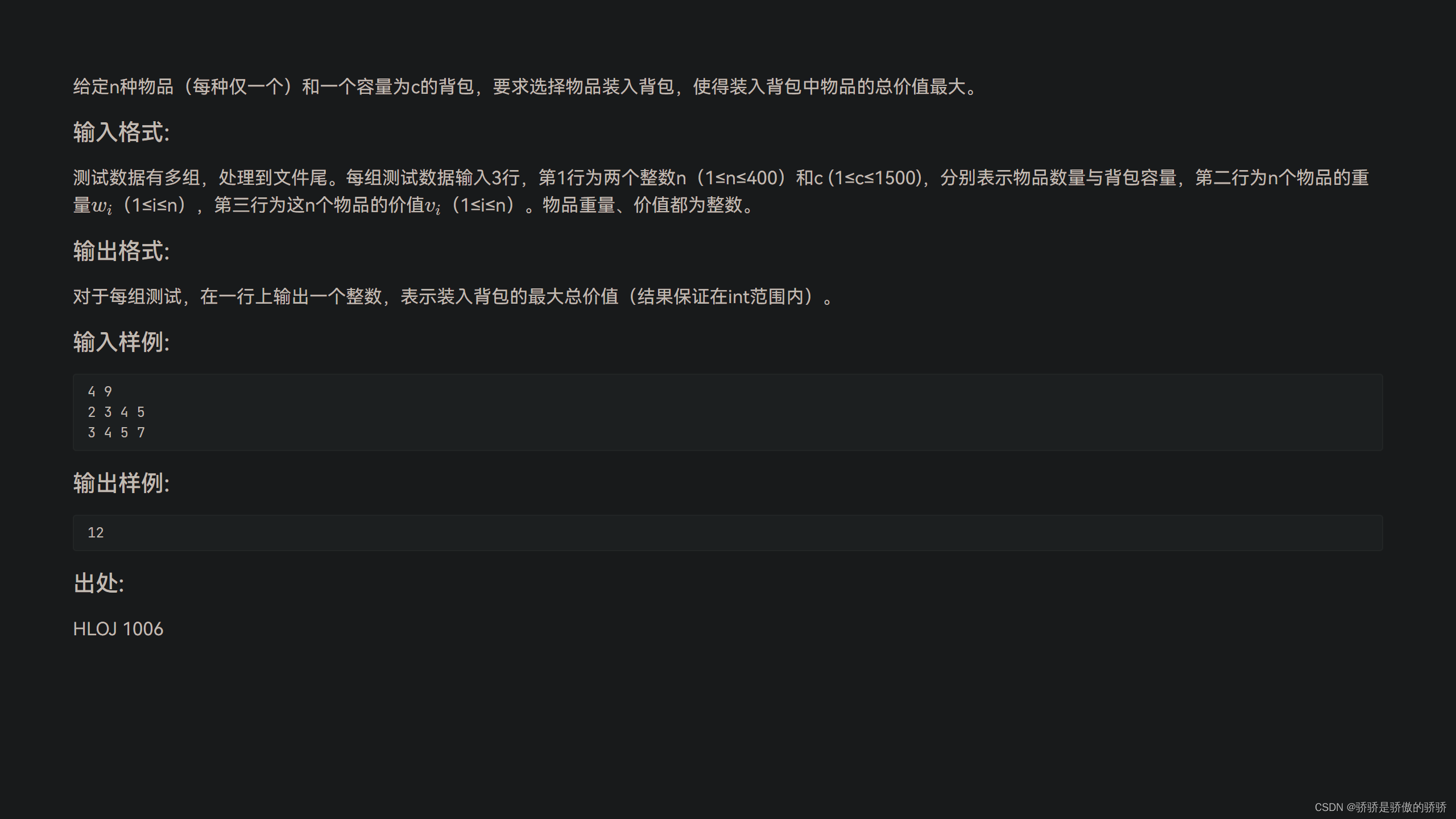
朴素 01 背包
dp[i][j] 指前 i 个物品在容量 j 下的最大价值
dp[i][j] 可以通过两种状态转移而来
1：dp[i-1][j] 在不选择第i个物品的情况下，dp[i][j] 就是在 j 容量下，只选择前 i-1 个物品的最大价值
2：dp[i-1][j-V[i]] + W[i] 若一定要选择 i 物品，即 i 物品一定要存在于背包中，可以形象的理解为，拿出现在背包中体积之和刚好为 V[i] 的物品集合，即让背包中存在一个 V[i] 大小的空间，那么就是 j-V[i]。显然，如果当前背包容量小于V[i]，是不可能放下的

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int N=2e3+10;

// 前i个物品在容量j的背包下的最大价值
int dp[N][N];

// 体积 价值
int V[N], W[N];

void solve(int n){
    //memset(dp, 0, sizeof dp);
    
    int m; // 容量
    cin>>m;
    for(int i=1; i<=n; i++) scanf("%d", &V[i]);
    for(int i=1; i<=n; i++) scanf("%d", &W[i]);
    
    for(int i=1; i<=n; i++)
        for(int j=0; j<=m; j++){
            dp[i][j]=dp[i-1][j];
            if( j >= V[i] )
                dp[i][j]=max( dp[i-1][j], dp[i-1][j-V[i]]+W[i] );
        }

    cout<<dp[n][m]<<endl;
}

int main(){
    int n;
    while(cin>>n) 
        solve(n);
    return 0;
}

7.最长有序子序列

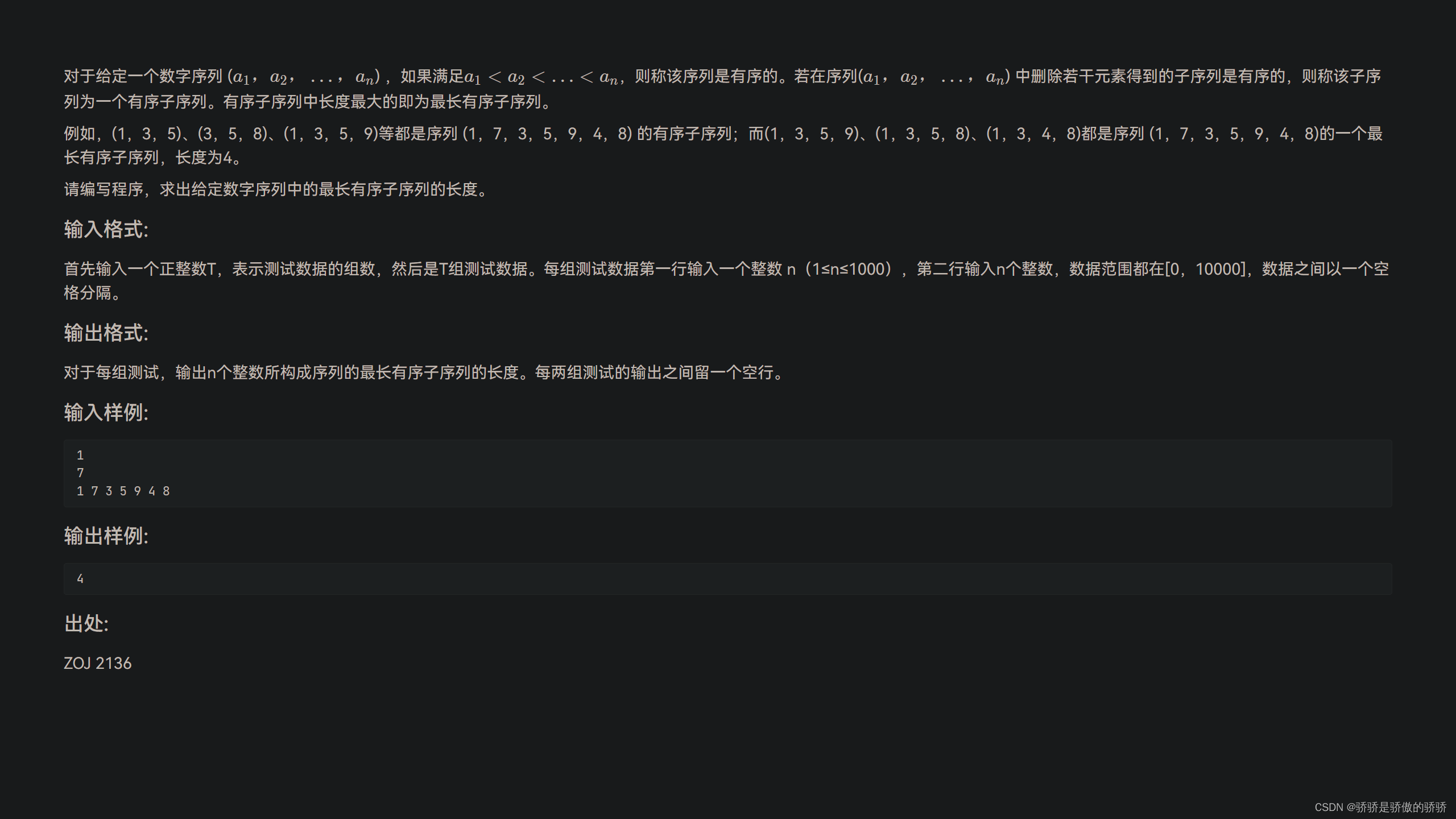
最长上升子序列 LIS
值得注意，dp[i]的含义是，以 g[i] 结尾的序列 的最长长度，因此 dp[n] 并不是最长长度

#include <iostream>
#include <cstring>
using namespace std;

const int N=1e3+10;

int g[N];
// 以 i 结尾 的最长子序列长度
int dp[N];

int T;

bool sb=0;

void solve(int t){
    memset(dp, 0, sizeof dp);
    //memset(g, 0, sizeof g);
    int n;
    cin>>n;
    for(int i=1; i<=n; i++) scanf("%d", &g[i]);

    for(int i=1; i<=n; i++){
        dp[i]=1;
        for(int j=1; j<i; j++)
            if(g[i]>g[j])
                dp[i]=max(dp[i], dp[j]+1);
        dp[0]=max(dp[0], dp[i]);
    }
    
    if(sb)
        cout<<"\n\n";
    cout<<dp[0];
    sb=1;
}

int main(){
    cin>>T; 
    while(T--)
        solve(T);
    return 0;
}

6.铺满方格

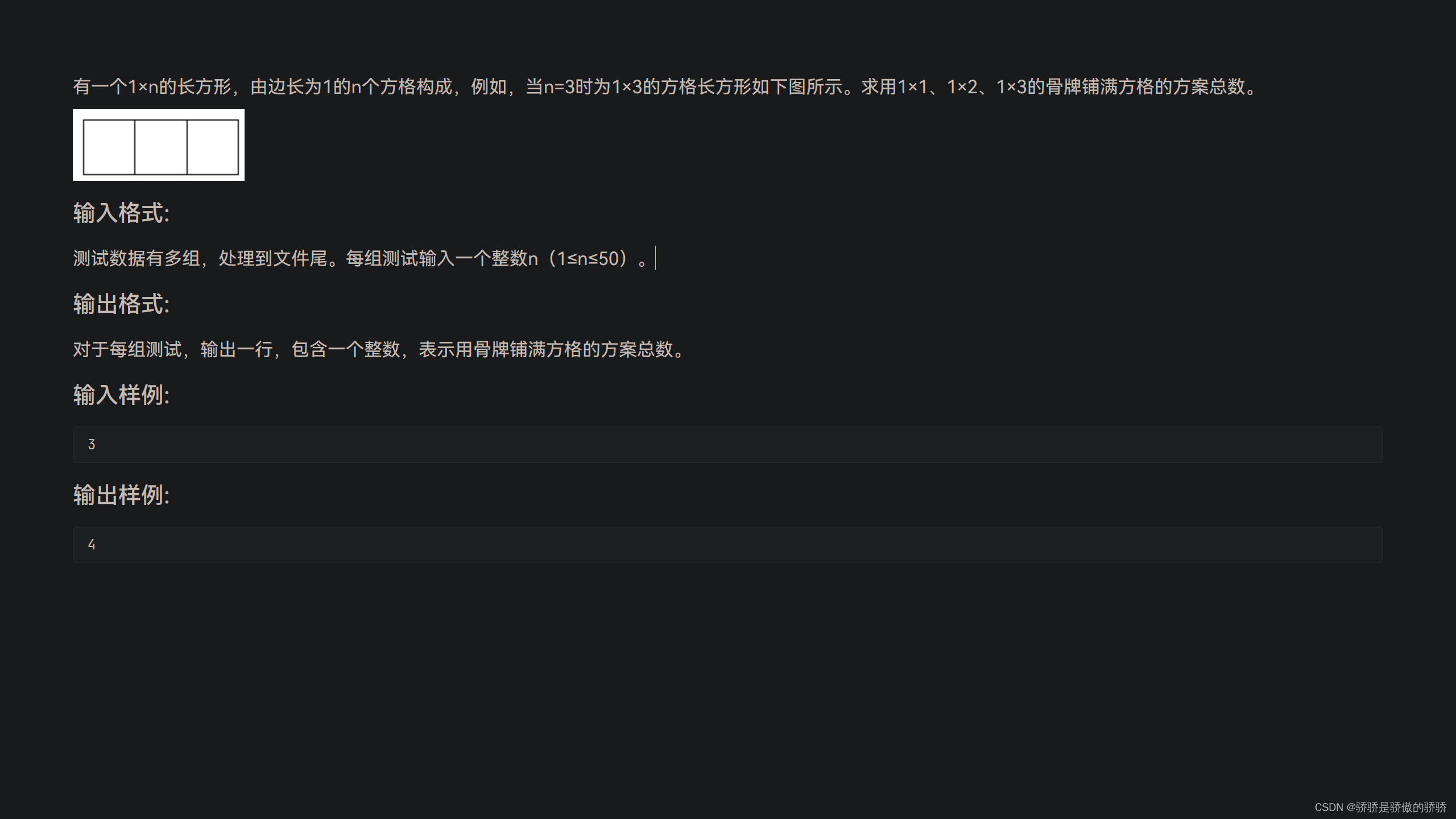
经典DP，当前状态可以由前面三种状态转移而来
dp[i]=dp[i-1]+dp[i-2]+dp[i-3]

#include <iostream>
#include <cstring>
using namespace std;

typedef long long LL;

const int N=60;
// 铺满前 i 长度的格子有 dp[i]种方案
LL dp[N];

void solve(int n){
    // 初始化
    dp[1]=1; // 1
    dp[2]=2; // 11 2
    dp[3]=4; // 111 12 21 3
    for(int i=4; i<=n; i++)
        dp[i]=dp[i-3]+dp[i-2]+dp[i-1];
    cout<<dp[n]<<endl;
}

int main(){
    int n;
    while(cin>>n) {
        memset(dp, 0, sizeof dp);
        solve(n);
    }
    return 0;
}

5.计算n!(n要能大于13）

这题竟然不让用python过

直接上高精度乘法就ok

#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;

vector<int> MUL(vector<int>&A, int b){
    // 倒叙输入A，正序b，倒叙输出res
    vector<int> res;
    int t=0;
    for(int i=0; i<A.size() || t; i++){
        if (i<A.size()) t+=A[i]*b;
        res.push_back(t % 10);
        t /= 10;
    }
    // 去前导0
    while (res.size() > 1 && res.back() == 0) res.pop_back();
    return res;
}

int main(){
    int n;
    cin>>n;
    
    vector<int> ans;
    ans.push_back(1);
    
    for(int i=1; i<=n; i++)
        ans=MUL(ans, i);
    
    for(int i=ans.size()-1; i>=0; i--)
        cout<<ans[i];
    
    return 0;
}

3.八皇后问题

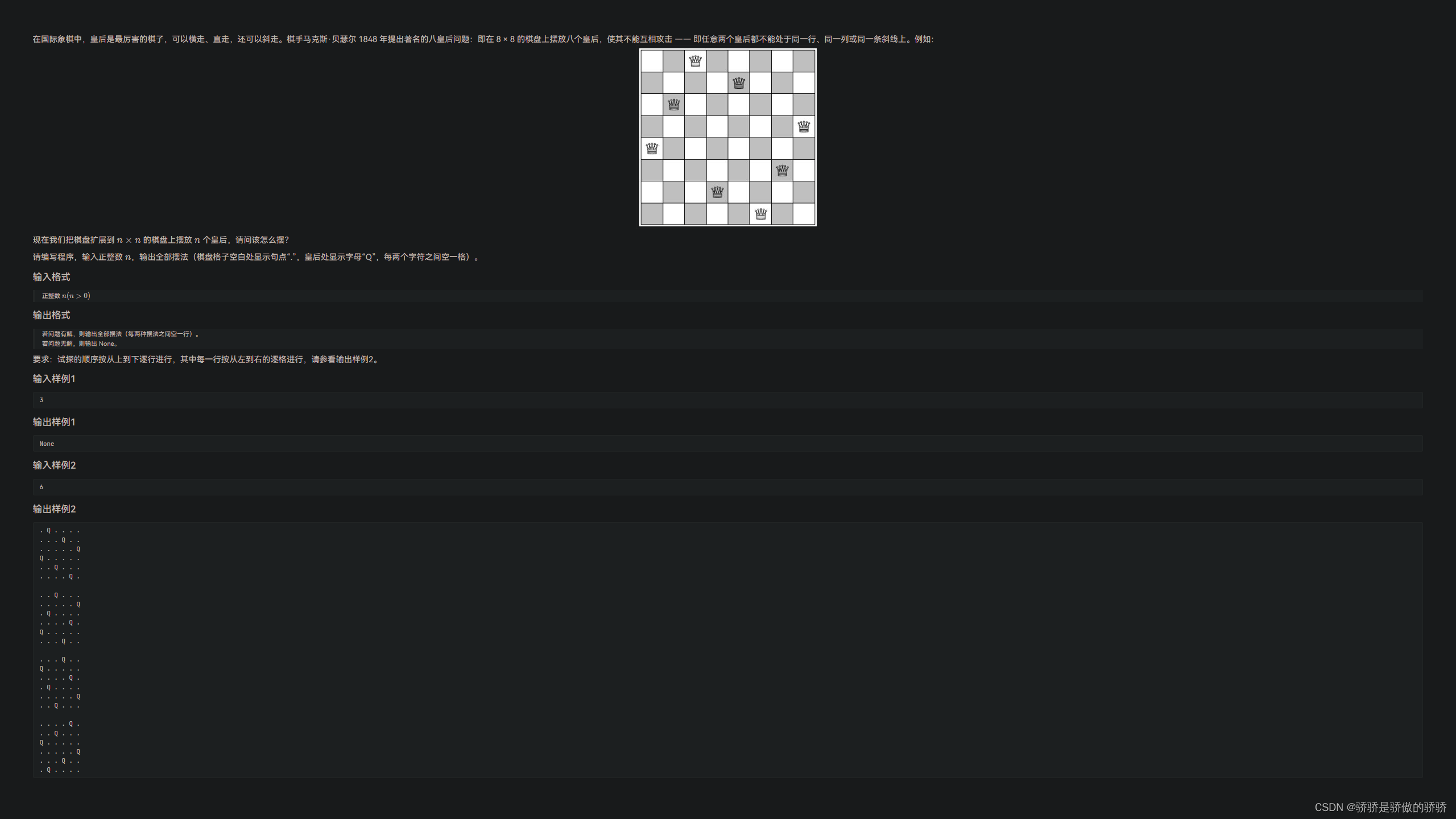
经典dfs，其中比较关键的是斜线状态的表示

主对角线可以用 r-c+10 唯一表示
副对角线可以用 r+c 唯一表示

明确了每个状态的表示，那么就可以从 (1, 1) 点开始，挨个搜索，这也是最朴素的搜索方法，但可惜，tle了
根据题意，每行必定只会存在一个queen，那么我们可以不一个一个的点搜，而是一行一行的搜，当前行若存在皇后，下一个皇后必定不在该行

#include <iostream>
using namespace std;

const int N=20;

int n, flg;

int g[N][N];
int row[N], col[N], x1[2*N], x2[2*N];

bool use(int r, int c){
    if(row[r] || col[c] || x1[r-c+10] || x2[r+c])
        return 1;
    return 0;
}

void change(int r, int c){
    g[r][c]^=1;
    row[r]^=1;
    col[c]^=1;
    x1[r-c+10]^=1;
    x2[r+c]^=1;
}

// 搜索行
void dfs(int r){

    if(r>n){
        if(flg!=0) puts(""); // 格式
        for(int i=1; i<=n; i++, puts(""))
            for(int j=1; j<=n; j++){
                if(g[i][j]) putchar('Q');
                else putchar('.');
                if(j!=n) putchar(' ');
            }
        flg=1;
        return ;
    }

    // 枚举状态
    for(int c=1; c<=n; c++)
        // 改变
        if(!use(r, c)){
            change(r, c);
            dfs(r+1);
            change(r, c); // 恢复现场
        }
}

int main(){
    cin>>n;
    
    dfs(1);

    if(!flg) puts("None");

    return 0;
}

2.哈夫曼编码

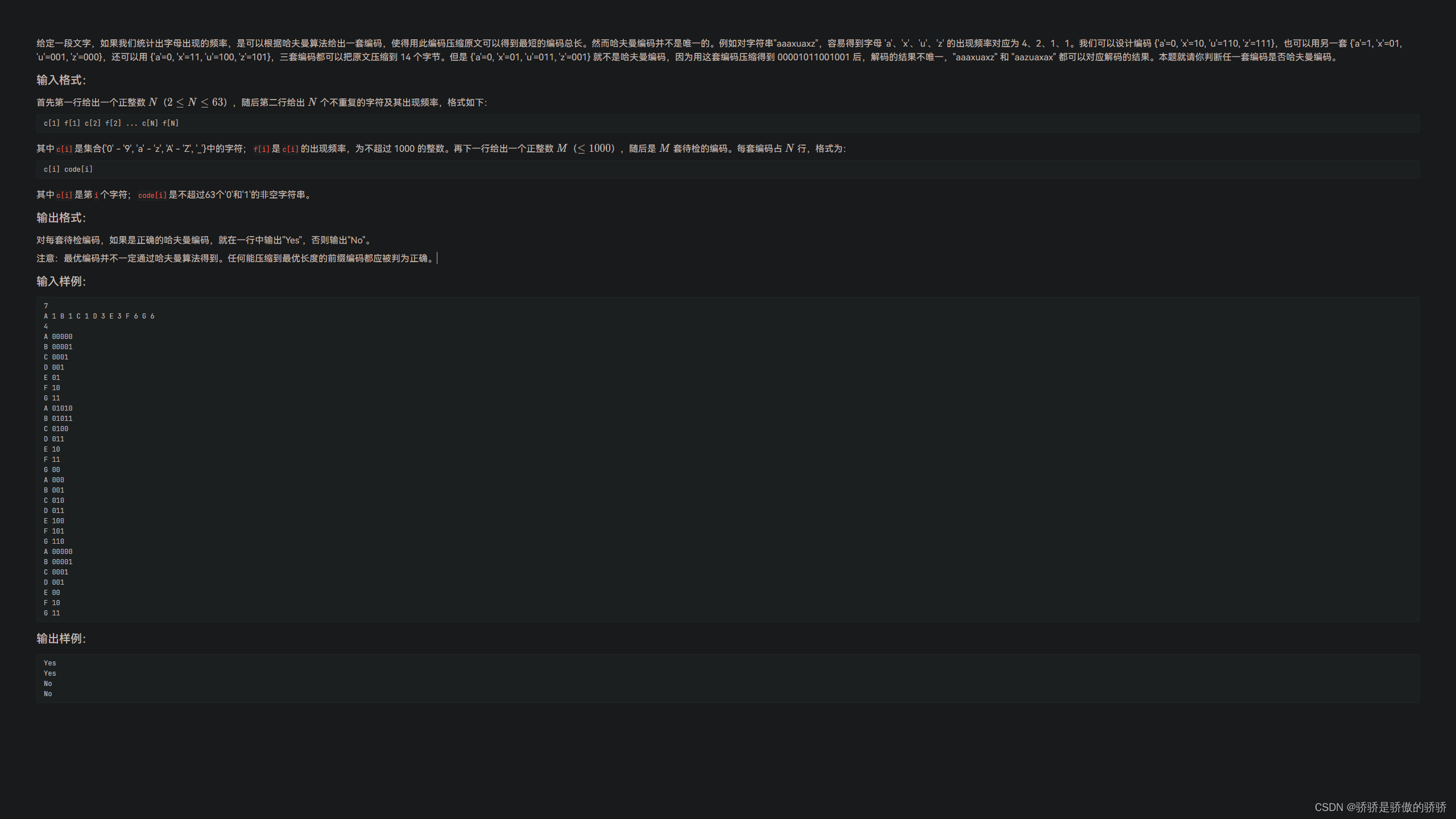
当用 n 个结点（都做叶子结点且都有各自的权值）试图构建一棵树时，如果构建的这棵树的wpl（带权路径长度）最小，称这棵树为“最优二叉树”，有时也叫“赫夫曼树”或者“哈夫曼树”

从定义出发，我们可以知道，若一颗树是最优二叉树，则wpl是一定的
通过从小到大建树，我们可以计算出该树的wpl
而计算题目给出编码方式的树的wpl，即每个叶子节点 出现频率 * 长度 之和

同时，对于每个编码，都不允许是其他编码的前缀

#include <iostream>
#include <queue>
#include <cstring>
using namespace std;

const int N=70;

int  f[N];

int n;
int wpl;

bool deal(string a, string b){
    int i=0;
    for( ; i<a.size(); i++)
        if(a[i]!=b[i]) break;
    
    // 全部匹配
    if( i==a.size() ) return 1;
    return 0;
}

int solve(){
    string str[N];
    // 首先计算wpl
    int s=0;
    for(int i=1; i<=n; i++){
        string tch;
        cin>>tch>>str[i];
        s+=f[i]*str[i].size();
    }
    if(s!=wpl) return 0;

    // 判断是否是前缀
    for(int i=1; i<=n-1; i++)
        for(int j=i+1; j<=n; j++){
            string a=str[i];
            string b=str[j];
            if(a>b) swap(a, b);
            // 如果 a 是 b 的前缀
            if( deal(a, b) ) return 0;
        }

    return 1;
}

int main(){
    scanf("%d", &n);
    
    // 小根堆
    priority_queue<int, vector<int>, greater<int>> q;
    
    for(int i=1; i<=n; i++){
        // 这个输入没任何用
        char tch[2]; scanf("%s", tch);
        scanf("%d", &f[i]);
        q.push(f[i]);
    }

    // wpl
    while(q.size()>=2){
        int a=q.top(); q.pop();
        int b=q.top(); q.pop();
        wpl+=a+b;
        q.push(a+b);
    }
    
    int m;
    scanf("%d", &m);
    for(int i=1; i<=m; i++)
        if( solve() )
            puts("Yes");
        else   
            puts("No");
    
    return 0;
}

1.愿天下有情人都是失散多年的兄妹

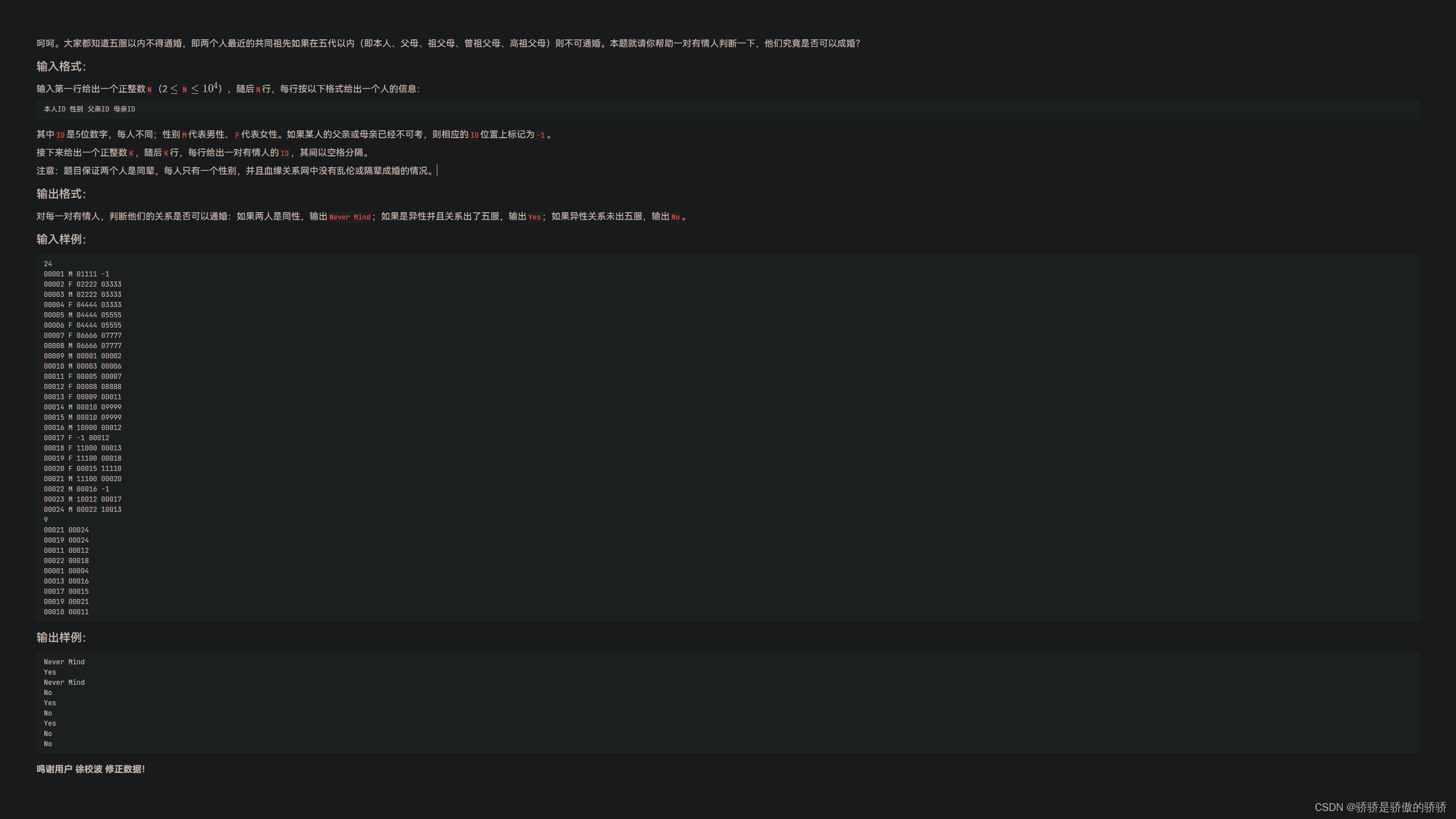
**题目，我就想知道样例中1号到底是男是女？？？

首先，存所有人的信息，因为ID是5位数字，且每人不同，因此我们可以用1e6大小的数组存
同时，存信息的时候，需要同时将父母的性别存入（如果没存的话）
值得注意，在这道题中，性别信息以直接给出的为准，而不是以 “父亲ID” 为准，换言之，“父亲ID”不一定对应男，“母亲ID”不一定对应女
在对两人进行判断时，首先判断是否同性
在判断是否近亲时，将其 id 与 代数 作为队列中的元素，直接宽搜或者深搜就ok
一个细节，第五代的父母不需要加入队列，但第五代需要判重

#define fst first
#define sed second

#include <iostream>
#include <queue>
#include <cstring>
using namespace std;

typedef pair<int, int> PII;

const int N=1e6+10;

struct node{
    char sex; // 性别
    int fa;   // 父亲id
    int mo;   // 母亲id
};

// 所有人的信息
node arr[N];
int used[N]; 

int deal(int a, int b){
    // Never Mind
    if(arr[a].sex==arr[b].sex) return 1;

    memset(used, 0, sizeof used);
    
    // id 代数 
    queue<PII> q;
    
    // 第一代
    used[a]++, used[b]++;
    q.push({a, 1}), q.push({b,1});
    
    // 找五代祖宗
    while(q.size()){
        auto t=q.front();
        q.pop();

        int moid=arr[ t.fst ].mo; // 这个人妈的id
        int faid=arr[ t.fst ].fa; // 这个人爸的id
        int dai =t.sed+1;           // 爸妈的代数

        if( moid!=-1 ){ // 继续找妈
            if(dai<=4) q.push({moid, dai}); // 第五代不用继续找妈了
            used[ moid ]++;
        }
        if( faid!=-1 ){ // 继续找爸
            if(dai<=4) q.push({faid, dai});
            used[ faid ]++;
        }
        
        // 五代内
        if(used[ moid ]>=2 || used[ faid ]>=2 )
            return 2;
    }

    return 3;
}

int main(){
    // 因为存在爸妈到顶了，预先所有位置的爸妈为-1
    for(int i=0; i<N; i++) arr[i].mo=-1, arr[i].fa=-1, arr[i].sex='s';

    int n;
    cin>>n;
    for(int i=1; i<=n; i++){
        int id;
        cin>>id;
        getchar(); // 读一个空格
        scanf("%c%d%d", &arr[id].sex, &arr[id].fa, &arr[id].mo); 
        
        if( arr[id].fa!=-1 && arr[ arr[id].fa ].sex=='s') arr[ arr[id].fa ].sex='F';
        if( arr[id].mo!=-1 && arr[ arr[id].mo ].sex=='s') arr[ arr[id].mo ].sex='M';
    }
    
    int k;
    cin>>k;
    for(int i=1; i<=k; i++){
        int a, b;
        scanf("%d%d", &a, &b);
        int flg=deal(a, b);
        
        if(flg==1) puts("Never Mind");
        if(flg==2) puts("No");
        if(flg==3) puts("Yes");
    }
    return 0;
}