[数据结构与算法]leetcode栈和队列

1.栈和队列常见方法

(1)栈：

stack.push()//压栈
stack.pop()//弹栈
stack.empty()==true//栈为空
stack.peek()//返回栈顶元素（只返回不删除）

（2）队列：

queue.add()：往队尾添加元素
queue.remove()：删除队头元素（并且返回队头元素）
queue.peek():返回队头元素（只返回不删除）



Queue queue=new LinkedList();
queue.add(1)
queue.add(2)
queue.add(3)
queue.add(4)
queue.add(5)
int size=queue.szie();
for(int i=0;i<size;i++)
{
  Systerm.out.println(queue.remove());
  //得到1，2，3，4，5
}

双端队列：

（1）队列只能在队尾添加元素，在队头删除元素，而双端队列在队头队尾都可以进行添加和删除操作

（2）双端队列Deque的常见方法：（在队列的add，peek，remove方法基础上进行改造）

//创建双端队列
Deque queue=new LinkedList();

//First表示队首，Last表示队尾

//在队首添加元素
queue.addFirst();  
//在队尾增加元素
queue.addLast();


//获取队首元素
queue.peekFirst();
//获取队尾元素
queue.peekLast();


//移除并且返回队首元素
queue.removeFirst();
queue.removeLast();

2.用两个栈实现队列：力扣（剑指offer09）

把栈和队列都想象成一个黑箱子

将1，2，3依次输入到这个黑箱子，如果这个黑箱子是栈，就依次返回3，2，1

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?如果这个黑箱子是队列，就依次返回1，2，3

加入元素的时候直接加入到stack1里面就行

主要是弹出元素时：弹出元素肯定是弹出stack2中的元素

如果stack2中有元素，就直接stack2.pop()

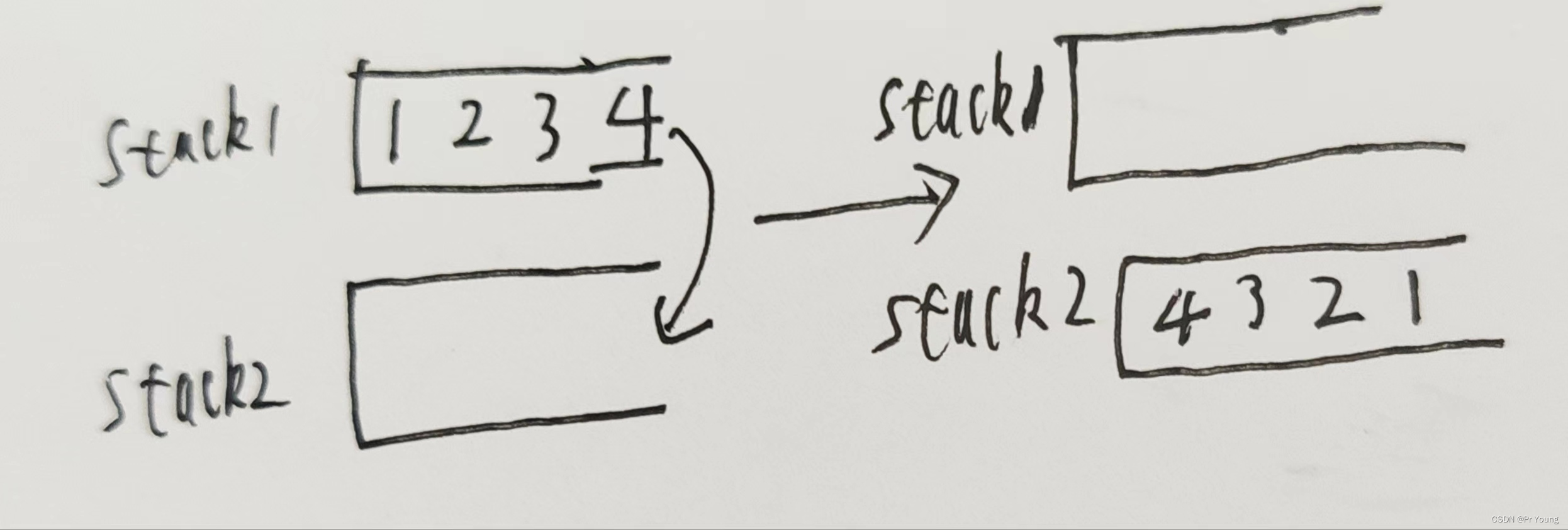
stack2为空的时候（即stack2中没有元素可以弹出的时候），把stack1中的元素全部转移到stack2中，然后再stack2.pop()

?将stack1内的元素全部转移到stack2内 ：

class CQueue 
{
     Stack<Integer> stack1;
     Stack<Integer> stack2;
    public CQueue() 
    {
       stack1=new Stack();
       stack2=new Stack();
    }
    //往你创建的队列中添加元素
    public void appendTail(int value)
    {
       stack1.push(value);
    }
    //往你创建的队列中弹出元素
    public int deleteHead() 
    {
        //要弹出元素，肯定是弹出stack2这个栈里面的栈顶元素

        //如果stack2栈内元素为空，stack1内也没元素，那就返回-1
        //如果stack2栈内元素为空，stack1内有元素，就把stack1内所有元素转移到stack2里面去

        /*比如stack1里面添加了四个元素1，2，3，4，现在显然是想要打印出1，2，3，4
          所以要把1，2，3，4全部从stack1中压入stack2中，这样不断stack2.pop()才能得到1，2，3，4*/
        if(stack2.empty()==true)
        {
          if(stack1.empty()==true)  return -1;
          else//如果stack1不为空
          {
              while(stack1.empty()==false)
              {
                 stack2.push(stack1.pop());
              }
          }
        }
        return stack2.pop();     
    }
}

//创建队列（调用构造方法）
CQueue obj = new CQueue();

//添加一个元素进队列队尾
obj.appendTail(value);

//删除队头元素并且返回这个队头元素
int param_2 = obj.deleteHead();

另外一道跟这个也很相似力扣（leetcode232）

class MyQueue 
{
    Stack<Integer> stack1;
    Stack<Integer> stack2;

    //调用构造方法创建两个栈
    public MyQueue() 
    {
       stack1=new Stack();
       stack2=new Stack();
    }
    
    public void push(int x)
    {
      stack1.push(x);
    }
    
    public int pop() 
    {
       //肯定是弹出stack2中的元素
       //stack2为空的时候（即stack2中没有元素可以弹出的时候），把stack1中的元素全部转移到stack2中
       if(stack2.empty()==true)
       {
          while(stack1.empty()==false)
          {
              stack2.push(stack1.pop());
          }
       }
        return  stack2.pop();
    }
    
    public int peek() 
    {
       if(stack2.empty()==true)
       {
          while(stack1.empty()==false)
          {
              stack2.push(stack1.pop());
          }
       } 
      return stack2.peek();
    }
    
    public boolean empty() 
    {
        if(stack1.empty()==true&&stack2.empty()==true)
        {
            return true;
        }
        return false;

    }
}

3.用两个队列实现栈

力扣225

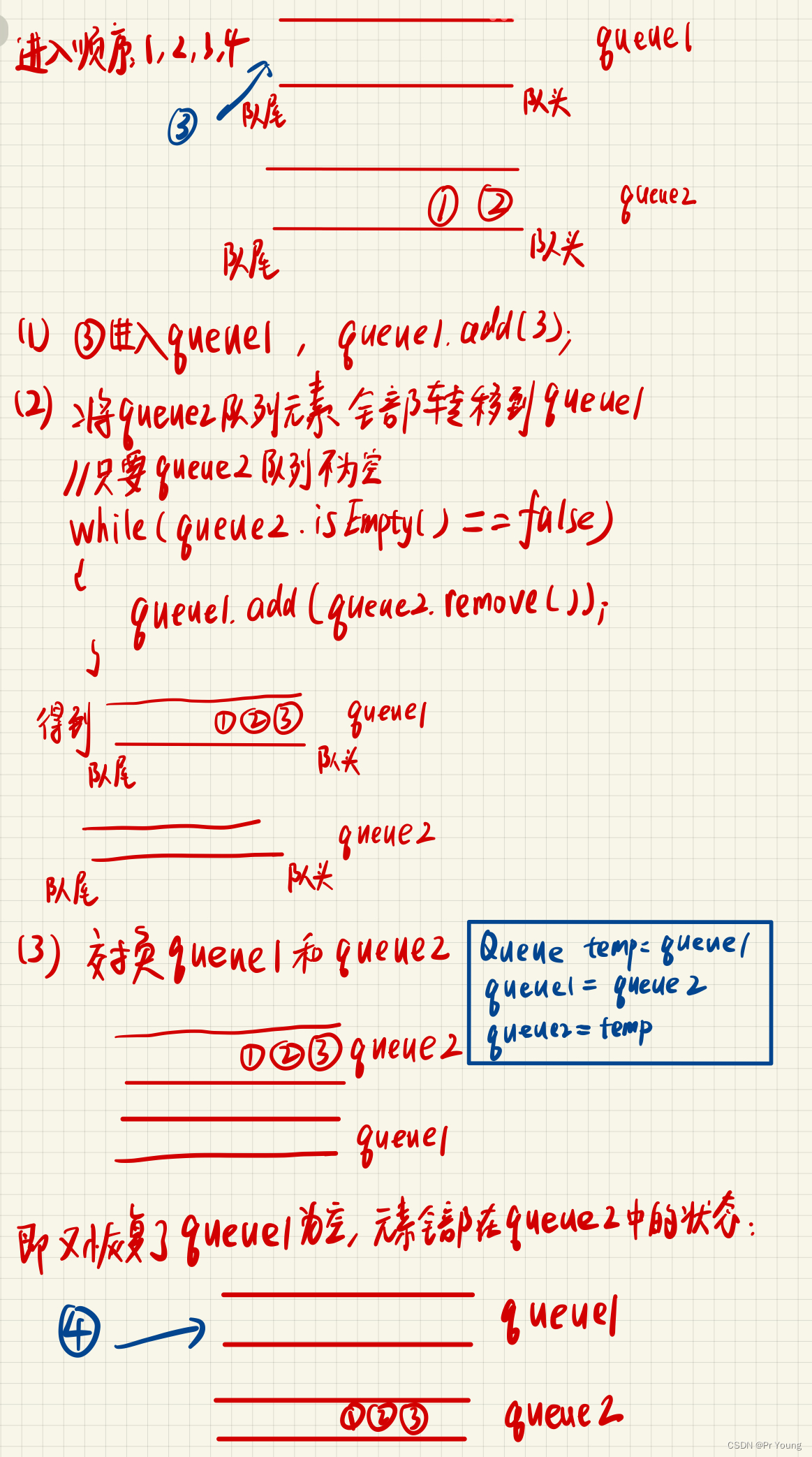
定义两个队列，其中queue1队列用来加入元素，queue2队列用来peek和pop弹出元素

?

class MyStack 
{
    Queue<Integer> queue1;
    Queue<Integer> queue2;
    public MyStack() 
    {
      queue1=new LinkedList();
      queue2=new LinkedList();
    }
    
    public void push(int x)
    {
       //step1:先把元素添加到queue1里面
       queue1.add(x);
       //step2：只要队列queue2里面还有元素，就要把它转移到队列queue1里面
       while(queue2.size()!=0)
       {
           queue1.add(queue2.remove());
       }
       //step3:此时元素就全部在队列queue1里面了，再交换queue1和queue2即可
       Queue temp=queue1;
       queue1=queue2;
       queue2=temp;
    }
    
    public int pop()
    {
      return queue2.remove();
    }
    
    public int top() 
    {
      return queue2.peek();
    }
    
    public boolean empty()
    {
        return queue2.size()==0;
    }
}

4.最小栈

力扣155

最小栈其实就是在栈的基础上多了一个获取最小元素的功能

这道题进行测试时

minStack minstack=new MinStack();
minstack(-2);
minstack(0);
ninstack(-3);
//先压三个元素进栈
//然后调用getMin()方法来获取栈内最小元素是多少
minstack.getMin();

?暴力方法：

class MinStack 
{
    Stack<Integer>stack;
    public MinStack() 
    {
        stack=new Stack();         
    }
    
    public void push(int val) 
    {
        stack.push(val);
    }
    
    public void pop()
    {
       stack.pop();
    }
    
    public int top()
    {
        return stack.peek();
    }
    
    public int getMin() 
    {
        ArrayList<Integer> a=new ArrayList();
        for(int i:stack)
        {
            a.add(i);
        }
        int temp=Integer.MAX_VALUE;
        for(int j:a)
        {
            temp=Math.min(temp,j);
        }
        return temp;
    }

显然暴力法时间复杂度为O(n)，因为遍历栈的时间复杂度为O(n)

题目规定要用常数时间内找到最小元素肯定是满足不了的

双栈法：用两个栈，一个栈是正常的栈，元素进栈和出栈都是正常的

另一个栈是特殊的栈，一个元素要想进这个栈必须小于这个栈的栈顶元素，

当正常栈弹出栈顶元素时，特殊栈要不要也弹出栈顶元素呢？当正常栈要弹出的栈顶元素等于特殊栈的栈顶元素时，特殊栈的栈顶元素也要弹出，不相等时，特殊栈的栈顶元素就不用弹出

class MinStack 
{
    Stack<Integer> stack1;
    Stack<Integer> stack2;
    public MinStack()//初始化两个栈，一个正常栈，一个特殊栈
    {
        stack1=new Stack();  
        stack2=new Stack();  
    }
    public void push(int x) 
    {
        //stack1正常栈，入栈时正常入栈就行
        stack1.push(x);
        
        if(stack2.empty())   stack2.push(x);
        else
        {
            if(x<=stack2.peek())  stack2.push(x);   
        }
    }
    public void pop() 
    {
        int temp=stack1.peek();
        stack1.pop();
        if(!stack2.empty()&&stack2.peek()==temp)  stack2.pop();
    }
    public int top() 
    {
        return stack1.peek(); 
    }
    public int getMin() 
    {
        return stack2.peek();
    }
}