141.环形链表

141.环形链表
如何判断链表是否带环呢？可采用快慢指针法。
快指针一次走二步，慢指针一次走一步，如果它们最终相遇，说明链表带环，否则不带环。
为什么这个可以判断呢？结论：如果链表带环，fast一定可以追上slow。
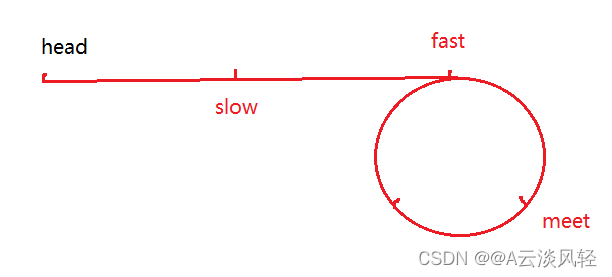
在这里插入图片描述
假设slow进环后，fast跟slow的距离是N
这时fast真正开始追击slow,fast一次走2步，slow一次走1步，它们之间的距离每次缩小1
N
N-1
N-2
…
2
1
0(追上相遇了）

如果快指针一次走3步，慢指针一次走1步，slow进环后，它们的距离每次缩小2，即使链表带环，也不一定能追上
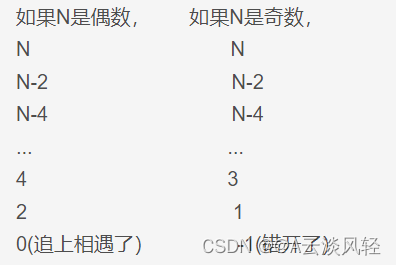
在这里插入图片描述
错开后，它们的距离变成C-1（C是环的长度），如果C-1是偶数，则可以追上，如果C-1是奇数，则永远追不上。
代码部分：

bool hasCycle(struct ListNode *head) {
    struct ListNode*slow,*fast;
    fast = slow = head;
    while(fast && fast->next)
    {
        fast = fast->next->next;
        slow = slow->next;

        if(fast == slow)
        {
            return true;
        }
    }

    return false;
}

142.环形链表 II

142.环形链表 II
如果链表带环，如何找到链表开始入环的第一个结点呢？
结论：一个指针从头结点开始一次走1步，一个指针从相遇点（快指针和慢指针都从头开始，快指针一次走二步，慢指针一次走一步，fast和slow相遇的点）开始一次走1步，它们两相遇的点即是链表开始入环的第一个结点。
证明：
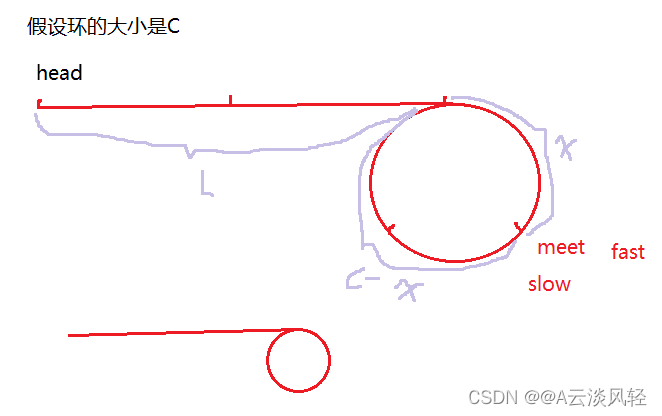
在这里插入图片描述
slow在进环以后，fast在2圈之内，一定追上slow!
为什么？追击的过程每次缩小1，不可能错过，它们的相对距离是1圈，slow最多走1圈，fast最多走2圈

假设slow在进环前，fast在环里面转了N圈（N>=1)，因为环可能很大，也可能很小。
slow 走的距离：L+X
fast 走的距离：L + NC +X
又因为fast是slow的2倍，则，2（L+X) = L + N*C +X,化简后得，L = (N-1)*C + C - X;证毕！。

代码部分：

struct ListNode *detectCycle(struct ListNode *head) {
    struct ListNode*fast,*slow;
    fast = slow = head;
    while(fast && fast->next)
    {
        fast = fast->next->next;
        slow = slow->next;

        if(fast == slow)
        {
            struct ListNode* meet = slow;
            while(head!=meet)
            {
               head = head->next;
               meet = meet->next;
            }

            return head;
        }
    }
    return NULL;
}