随处可见的红黑树详解
前言
??刚开始接触红黑树的时候,感觉很难。其实不然,红黑树只是情况分的多了一点而已,相较于线段树,主席树等等,简单多了。对于红黑树3种插入维护4种删除维护没必要去记忆,稍作了解,对于红黑树的性质和特点,需要特别记忆。
??本专栏知识点是通过零声教育的线上课学习,进行梳理总结写下文章,对c/c++linux课程感兴趣的读者,可以点击链接 C/C++后台高级服务器课程介绍 详细查看课程的服务。
注意,本文图中红黑树的叶子结点默认不画出来
为什么要有红黑树
二叉搜索树
??二叉搜索树(又叫二叉排序树,BST):对于任意一个结点,其左子树的值必定小于该结点,其右子树的值必定大于该结点。那么中序遍历的时候,就是有序的了。理论上来说,增加,删除,修改的时间复杂度都是O(log(N))。但是它存在一个致命的问题。
??退化:向树中插入[1,2,3,4,5,6],此时树退化成了一个链表,增加,删除,修改的时间复杂度退化为O(N)
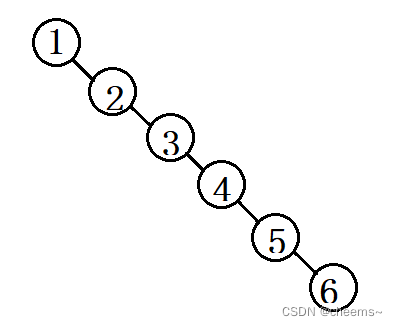
平衡二叉搜索树
??平衡二叉搜索树(AVL Tree):它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉搜索树。如果向树中插入[1,2,3,4,5,6]
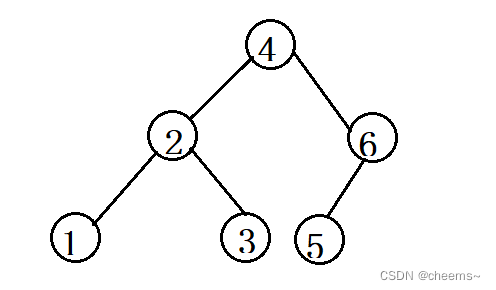
??可以看到AVLTree在最坏的情况下,依然保持了“绝对的平衡”:左右两个子树的高度差的绝对值不超过1。那么AVL Tree是如何保证平衡的呢,是通过旋转,可以看到,无论是插入还是删除元素,都要去通过旋转维护整个树的平衡。
-
AVL查询元素:O(log(N))
-
AVL插入元素:最多一次旋转O(1),加上查询的时间O(log(N)),插入的复杂度O(log(N))
-
AVL删除元素:必须检查从删除结点开始到根结点路径上的所有结点的平衡因子。因此删除的代价比较大,删除最多需要log(N)次旋转,加上查询的时间,删除的复杂度O(2log(N))
红黑树
??我们发现,AVL树未免太严格了一些,有没有一种数据结构,能让AVL树不那么严格平衡,降低维护平衡的开销,同时又不能像BST一样退化呢?
当然有,就是本文所写的红黑树(rbTree):
-
rbTree查询元素:O(log(N))
-
rbTree插入元素:插入最多2次旋转,加上查询的时间O(log(N)),插入的复杂度O(log(N))
-
rbTree删除元素:删除最多需要3次旋转,加上查询的时间,删除的复杂度O(log(N))
??虽然插入和删除元素后,需要旋转和变色(本文中统一为维护),但是这一时间复杂度可以估算为O(1)不计
??因为rbTree的第6条性质(见下文)
- 所以红黑树的查询效率略低与AVL的查询
- 红黑树和AVL插入的速度差不多
- 红黑树删除的速度比AVL快,因为AVL删除最多需要og(N)次旋转
红黑树的应用场景
- c++ stl map,set(红黑树的封装)
- 进程调度cfs(用红黑树存储进程的集合,把调度的时间作为key,那么树的左下角时间就是最小的)
- 内存管理(每次使用malloc的时候都会分配一块小内存出来,那么这么块就是用红黑树来存,如何表述一段内存块呢,用开始地址+长度来表示,所以key->开始地址,val->大小)
- epoll中使用红黑树管理socketfd
- nginx中使用红黑树管理定时器,中序遍历第一个就是最小的定时器
红黑树的性质(重点)
1. 每个结点是红的或者黑的
2. 根结点是黑的
3. 每个叶子结点是黑的(因为这条性质,一般用叶子结点在代码中被特殊表示)
4. 如果一个结点是红的,则它的两个儿子都是黑的(不存在相邻红色)
5. 从任一节点到叶子节点,所包含的黑色节点数目相同(即黑高度相同)
6. 最长路径长度不超过最短路径长度的2倍(2n-1,一条黑红黑红…一条全黑)
红黑树的定义
#define RED 0
#define BlACK 1
typedef int KEY_TYPE;
typedef struct _rbtree_node {
unsigned char color;//颜色
struct _rbtree_node *left;//左子树
struct _rbtree_node *right;//右子树
struct _rbtree_node *parent;//父结点
KEY_TYPE key;
void *value;
} rbtree_node;//红黑树结点
typedef struct _rbtree {
rbtree_node *root;//根结点
rbtree_node *nil;//通用叶子结点
} rbtree;//红黑树
红黑树的左旋与右旋
动三个方向,改6个指针。
通过旋转,调整左右高度,使树达到平衡。
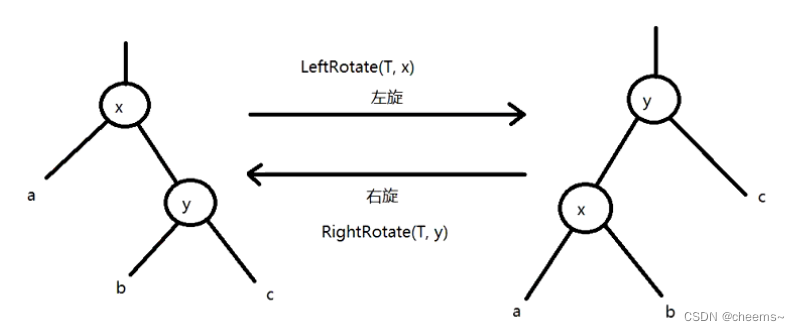
左旋leftRotate(T,x)—中右->左中
降低X结点的高度,提高X结点右结点(即Y)的高度。
- x的右子树指向y的左子树
- 本来指向x结点的父指针,改成指向y
- y的左子树指向x结点

右旋rightRotate(T,y)—中左->中右
降低Y结点的高度,提高Y结点左结点(即X)的高度。
- y的左子树指向x的右子树
- 本来指向y结点的父指针,改成指向x
- x的右子树指向y结点

//左旋leftRotate(T,x)---中右->左中
//降低X结点的高度,提高X结点右结点(即Y)的高度。
void _left_rotate(rbtree *T, rbtree_node *x) {
rbtree_node *y = x->right;
//1
x->right = y->left;//x的右子树指向y的左子树
if (y->left != T->nil) {
y->left->parent = x;//y的左子树的父节点指向x
}
//2
y->parent = x->parent;//y的父结点指向x的父结点
if (x->parent == T->nil) {//如果x是根结点
T->root = y;
} else if (x == x->parent->left) {
x->parent->left = y;//本来指向x结点的父指针,改成指向y
} else {
x->parent->right = y;
}
//3
y->left = x;//y的左子树指向x结点
x->parent = y;//x的父节点指向y
}
//右旋
//copy左旋的代码
//left改成right,right改成left
//x改成y,y改成x
void _right_rotate(rbtree *T, rbtree_node *y) {
rbtree_node *x = y->left;
//1
y->left = x->right;
if (x->right != T->nil) {
x->right->parent = y;
}
//2
x->parent = y->parent;
if (y->parent == T->nil) {
T->root = x;
} else if (y == y->parent->right) {
y->parent->right = x;
} else {
y->parent->left = x;
}
//3
x->right = y;
y->parent = x;
}
红黑树插入结点与插入维护红黑树的三种情况
插入结点
??在插入结点时,我们始终认为“插入这个结点之前,原来的红黑树是满足红黑树性质的==”,那么插入的位置容易找,就是不断的对比key,最终找到位置,那么新增的结点是什么颜色呢?我们通过性质发现:
- 如果新结点是黑色,违背了第5条性质
- 如果新结点是红色,可能违背第4条性质
而第四条性质,我们可以通过旋转与上色的方式修复,所以在我们插入结点的时候,我们始终认为新结点是红色
//因为传入的key可能是字符,可能是整形,所以要提取出来
//这里可以看出,其实可以封装成一个模板
int key_compare(KEY_TYPE a, KEY_TYPE b) {
//这里假设是int
if (a > b) {
return 1;
} else if (a < b) {
return -1;
} else {
return 0;
}
}
void rbtree_insert(rbtree *T, rbtree_node *z) {
//找位置
rbtree_node *x = T->root;
rbtree_node *y = T->nil;//y是x的父节点
while (x != T->nil) {//二分找位置
y = x;
if (key_compare(z->key, x->key) < 0) {
x = x->left;
} else if (key_compare(z->key, x->key) > 0) {
x = x->right;
} else {
//如果key相等,看自己的业务情景
//重复插入可以不修改直接退出,可以修改val
return;
}
}
//插入
z->parent = y;
if (y == T->nil) {
T->root = z;
} else if (key_compare(z->key, y->key) < 0) {
y->left = z;
} else {
y->right = z;
}
z->left = T->nil;
z->right = T->nil;
z->color = RED;
//维护红黑树
rbtree_insert_fixup(T, z);
}
插入结点后维护红黑树
??我们知道新增结点是红色,如果新结点是父节点也是红色,那么就需要维护红黑树了。
??如果父结点是爷结点是左子树,可以归纳出来三种情况。同理如果父结点是爷结点是右子树,我们也可以归纳出来三种情况。但是这三种情况的差异就是旋转方向的区别而已。一共是6种情况,但是归纳出来其实是3种,读者不要搞错了。
在下面的图中:z表示新增结点,y表示叔结点
父结点是爷结点是左子树
1. 叔结点是红色的
- 将叔结点和父结点变黑,爷结点变红
- 将当前结点变成爷结点(因为爷结点是红,爷结点的父节点也可能是红,所以要递归维护)
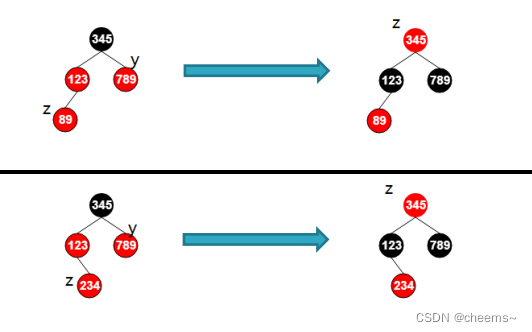
2. 叔结点是黑色的且新结点是左子树
- 将父结点变成黑色,爷结点变成红色
- 以爷结点为中心右旋
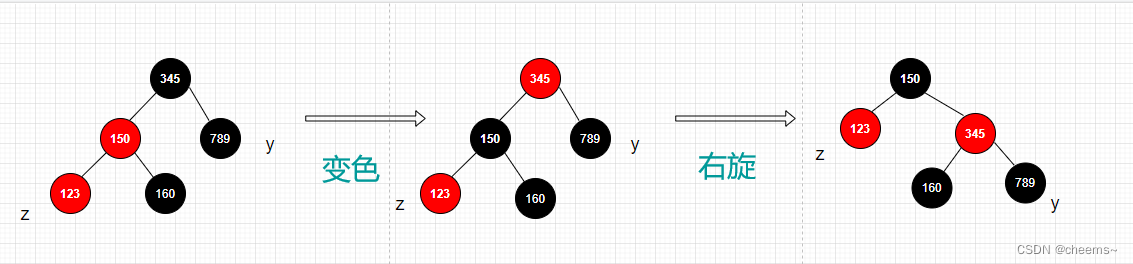
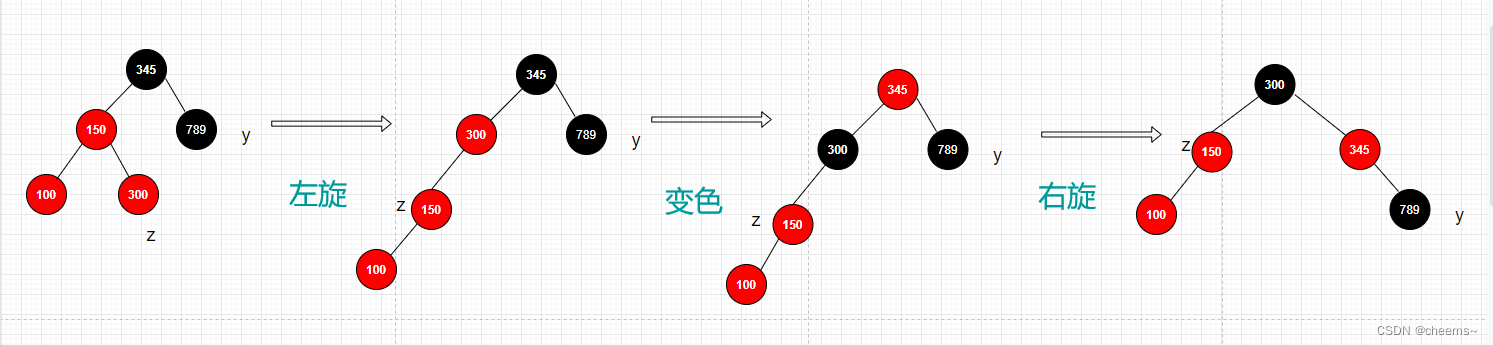
3. 叔结点是黑色的且新结点是右子树
- 以父结点为中心左旋
- 将父结点变黑色,爷结点变红色
- 以爷结点为中心右旋
父结点是爷结点是右子树
1. 叔结点是红色的
- 将叔结点和父结点变黑,爷结点变红
- 将当前结点变成爷结点(因为爷结点是红,爷结点的父节点也可能是红,所以要递归维护)
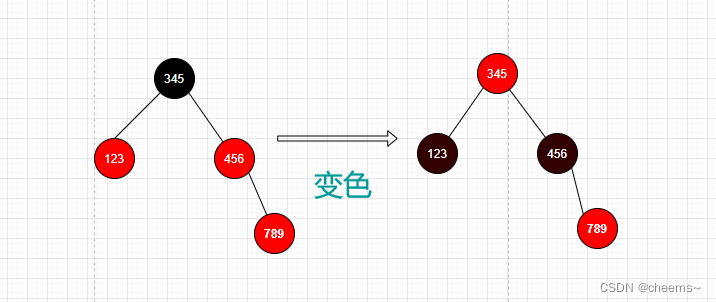
2. 叔结点是黑色的且新结点是左子树
- 以父结点为中心右旋
- 将父结点变黑色,爷结点变红色
- 以爷结点为中心左旋
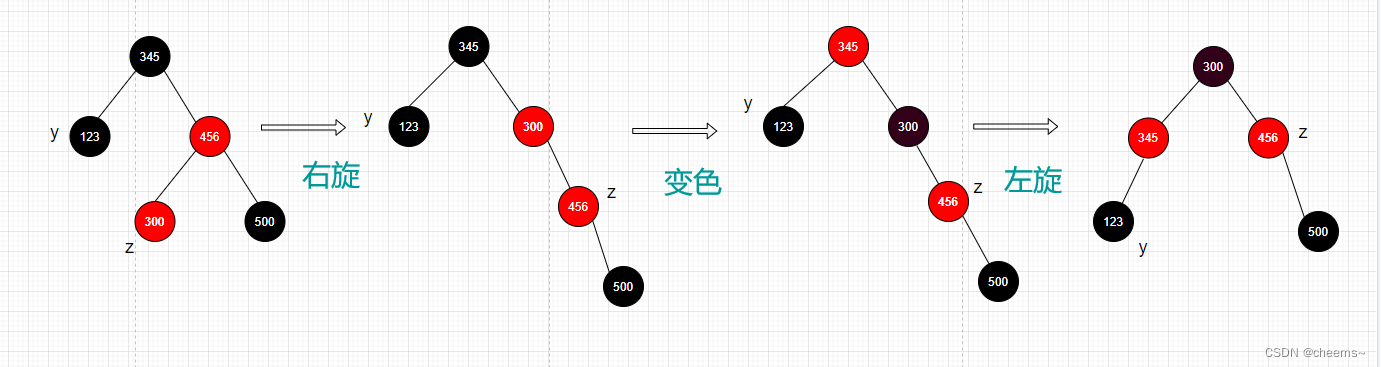
3. 叔结点是黑色的且新结点是右子树
- 将父结点变成黑色,爷结点变成红色
- 以爷结点为中心左旋
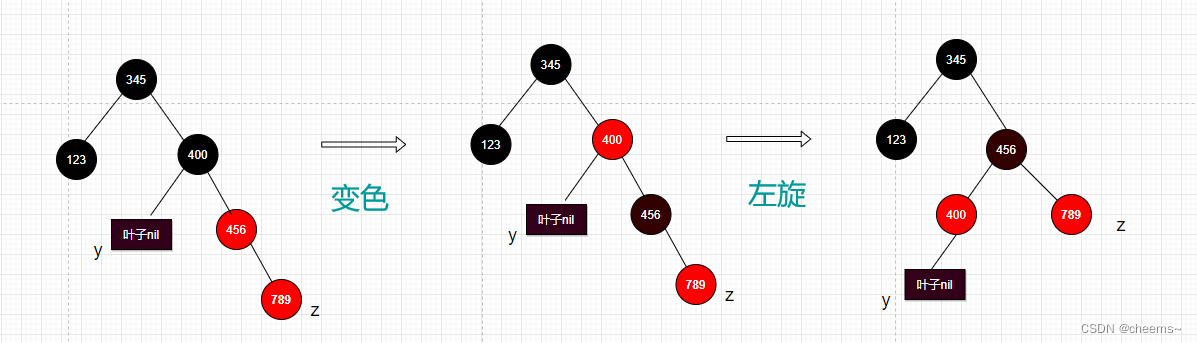
维护代码
//修复第4条性质
void rbtree_insert_fixup(rbtree *T, rbtree_node *z) {
while (z->parent->color == RED) {//父结点是红色的,需要调整
if (z->parent == z->parent->parent->left) {//如果父结点是爷结点是左子树
rbtree_node *y = z->parent->parent->right;//叔结点
if (y->color == RED) {//叔结点是红色的
//先变色,叔,父变黑
z->parent->color = BLACK;
y->color = BLACK;
//爷结点变红
z->parent->parent->color = RED;
//下面的调整完了,调整上面
z = z->parent->parent;
} else {//叔父结点是黑色
if (z == z->parent->right) {//新节点是在右边
z = z->parent;
rbtree_left_rotate(T, z);
}
z->parent->color = BLACK;
z->parent->parent->color = RED;
rbtree_right_rotate(T, z->parent->parent);
}
} else {
// 如果父结点是爷结点是右子树
rbtree_node *y = z->parent->parent->left;//叔父结点
if (y->color == RED) {//叔父结点是红色的
//先变色,叔,父变黑
z->parent->color = BLACK;
y->color = BLACK;
//爷结点变红
z->parent->parent->color = RED;
//下面的调整完了,调整上面
z = z->parent->parent;
} else {//叔父结点是黑色
if (z == z->parent->left) {//新节点是在左边
z = z->parent;
rbtree_right_rotate(T, z);
}
z->parent->color = BLACK;
z->parent->parent->color = RED;
rbtree_left_rotate(T, z->parent->parent);
}
}
}
//最后别忘了根节点始终是黑色
T->root->color = BLACK;
}
红黑树删除结点与删除维护红黑树的四种情况
删除结点
我们定义:
- 覆盖结点:z(被指定删除的结点,实际上被覆盖)
- 删除结点:y(实际上被删除的结点,一般是后继结点)
- 轴心结点:x(维护红黑树的结点)
红黑树删除结点根据改结点的左右子树分为三种情况:
- 没有左右子树
- 有且仅有一个子树
- 左右子树都有
对不同情况的处理:
- 情况1:直接删除该结点
- 情况2:将该结点的唯一子树挂到父结点上,然后删除该结点
- 情况3:找一个删除结点y(后继结点)覆盖 指定结点z,然后删除 删除结点y,对于这个删除结点y来说,它的情况一定是情况1或情况2
删除代码
rbtree_node *rbtree_mini(rbtree *T, rbtree_node *x) {
while (x->left != T->nil) {
x = x->left;
}
return x;
}
//找后继结点
rbtree_node *rbtree_successor(rbtree *T, rbtree_node *x) {
rbtree_node *y = x->parent;
//右子树不为空,则找右子树中最左的元素
if (x->right != T->nil) {
return rbtree_mini(T, x->right);
}
//找到结点第一个父结点
while ((y != T->nil) && (x == y->right)) {
x = y;
y = y->parent;
}
return y;
}
//覆盖结点z
//删除结点y
//轴心结点x
rbtree_node *rbtree_delete(rbtree *T, rbtree_node *z) {
rbtree_node *y = T->nil;
rbtree_node *x = T->nil;
if ((z->left == T->nil) || (z->right == T->nil)) {
y = z;//如果没有孩子或只有一个
} else {//如果有两个子树则找后继
y = rbtree_successor(T, z);
}
//一般x是y的右子树,找到轴心结点
if (y->left != T->nil) {
x = y->left;
} else if (y->right != T->nil) {
x = y->right;
}
//将该结点的唯一子树挂到父结点上,然后删除该结点
x->parent = y->parent;
if (y->parent == T->nil) {//根结点
T->root = x;
} else if (y == y->parent->left) {
y->parent->left = x;
} else {
y->parent->right = x;
}
//进行覆盖操作
if (y != z) {
z->key = y->key;
z->value = y->value;
}
//黑色才需要调整
if (y->color == BLACK) {
rbtree_delete_fixup(T, x);
}
return y;
}
删除结点后维护红黑树
??想一想,删除一个结点,该结点是什么颜色的时候才需要维护红黑树呢?
- 如果是红色,没有违反任何性质。所以如果是红色直接删除即可,无需维护
- 如果是黑色,黑色被删除,那么必定违反第5条性质,破坏了黑高,所以我们需要针对这一情况进行维护
??如果当前结点是父结点的左子树的情况,可以归纳出来四种情况。同理如果当前结点是父结点的右子树,我们也可以归纳出来四种情况。但是这四种情况的差异就是旋转方向的区别而已(镜像的)。一共是8种情况,但是归纳出来其实是4种,读者不要搞错了。
当前结点是父结点的左子树的情况
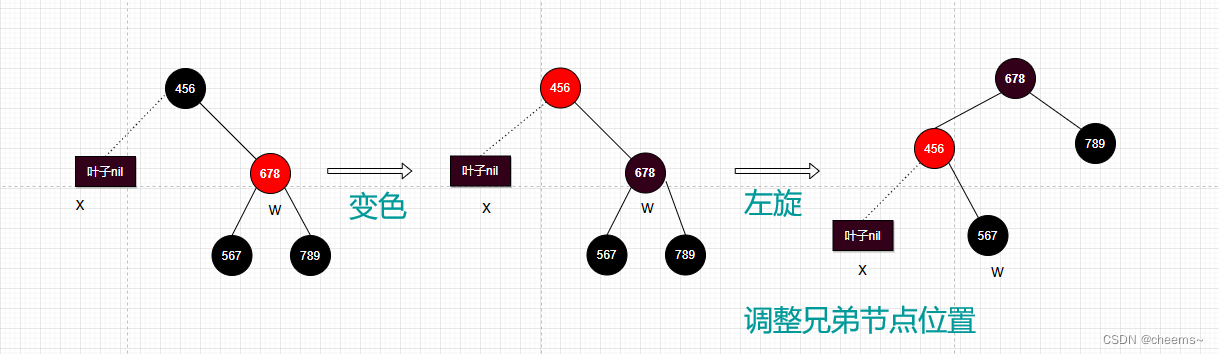
1. 当前结点的兄弟结点是红色的
- 兄弟节点变成黑色
- 父节点变成红色
- 父节点做左旋
- 将兄弟结点调整为父节点的右子树
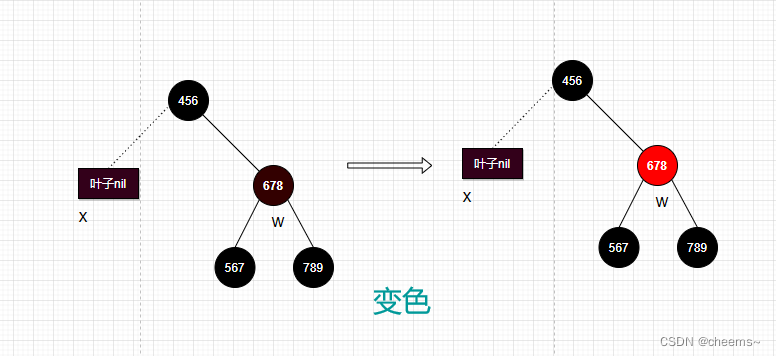
2. 当前结点的兄弟结点是黑色的,而且兄弟结点的两个孩子结点都是黑色的
- 兄弟节点变成红色
- 轴心结点变为父节点
3. 当前结点的兄弟结点是黑色的,而且兄弟结点的左孩子是红色的,右孩子是黑色的
-
将左孩子涂黑
-
将兄弟节点变红
-
对兄弟节点右旋
-
将兄弟结点调整为父节点的右子树
-
现在情况3就会变成情况4,接着做情况4的步骤
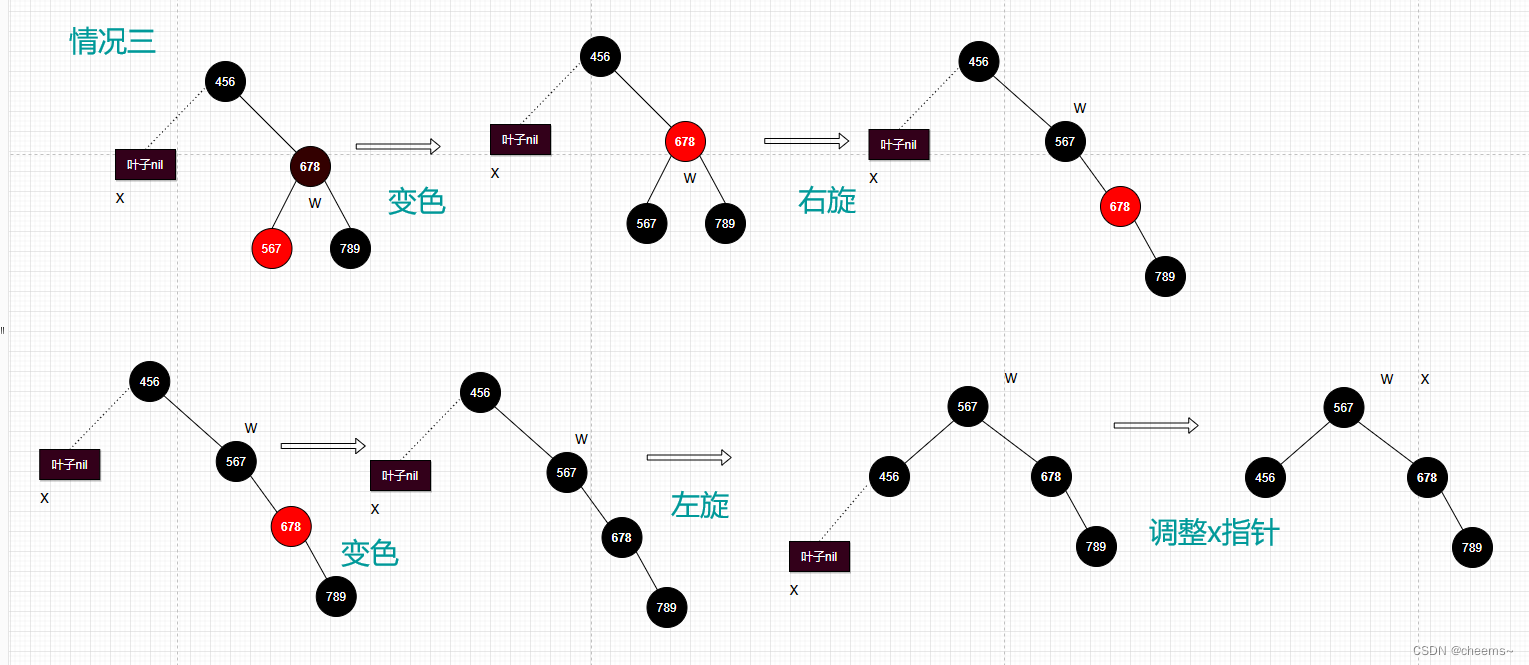
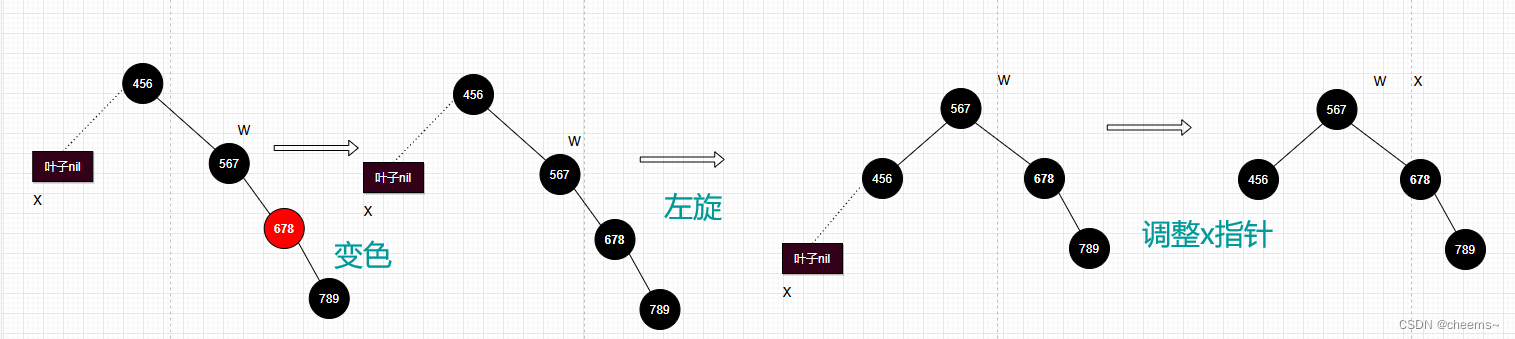
4. 当前结点的兄弟结点是黑色的,而且兄弟结点的左孩子是黑色的,右孩子是红色的
- 将兄弟节点换成父节点的颜色
- 把父节点和兄弟节点的右孩子涂黑
- 对父节点做左旋
- 设置x指针,指向根节点
当前结点是父结点的右子树的情况
1. 当前结点的兄弟结点是红色的
-
兄弟节点变成黑色
-
父节点变成红色
-
父节点做右旋
-
将兄弟结点调整为父节点的左子树
2. 当前结点的兄弟结点是黑色的,而且兄弟结点的两个孩子结点都是黑色的
-
兄弟节点变成红色
-
轴心结点变为父节点
3. 当前结点的兄弟结点是黑色的,而且兄弟结点的左孩子是黑色的,右孩子是红色的
-
将右孩子变黑
-
将兄弟节点变红
-
对兄弟结点左旋
-
将兄弟结点调整为父节点的左子树
-
现在情况3就会变成情况4,接着做情况4的步骤
4. 当前结点的兄弟结点是黑色的,而且兄弟结点的左孩子是红色的,右孩子是黑色的
-
将兄弟节点换成父节点的颜色
-
把父节点和兄弟节点的左孩子变黑
-
对父节点做右旋
-
将轴心结点调整为根结点
维护代码
void rbtree_delete_fixup(rbtree *T, rbtree_node *x) {
//如果x是红色,变成黑色,如果x是黑色,需要调整
while ((x != T->root) && (x->color == BLACK)) {
//当前结点是父结点的左子树
if (x == x->parent->left) {
//兄弟节点
rbtree_node *w = x->parent->right;
// 情况1:兄弟节点为红色
if (w->color == RED) {
// 兄弟节点变成黑色
w->color = BLACK;
// 父节点变成红色
x->parent->color = RED;
// 父节点做左旋
rbtree_left_rotate(T, x->parent);
//将兄弟结点调整为父节点的右子树
w = x->parent->right;
}
// 情况2:兄弟节点是黑色的,且兄弟的左孩子和右孩子都是黑色
if ((w->left->color == BLACK) && (w->right->color == BLACK)) {
// 兄弟节点变成红色
w->color = RED;
// 轴心结点变为父节点
x = x->parent;
} else {
// 情况3:x的兄弟节点是黑色的,兄弟的左孩子是红色,右孩子是黑色
if (w->right->color == BLACK) {
// 将左孩子涂黑
w->left->color = BLACK;
// 将兄弟节点变红
w->color = RED;
// 对兄弟节点右旋
rbtree_right_rotate(T, w);
// 重新设置x的兄弟节点
w = x->parent->right;
}
// 情况4:x的兄弟节点是黑色;x的兄弟节点的右孩子是红色的
// 将兄弟节点换成父节点的颜色
w->color = x->parent->color;
// 把父节点和兄弟节点的右孩子涂黑
x->parent->color = BLACK;
w->right->color = BLACK;
// 对父节点做左旋
rbtree_left_rotate(T, x->parent);
// 设置x指针,指向根节点
x = T->root;
}
} else {//当前结点是父结点的右子树
//兄弟节点
rbtree_node *w = x->parent->left;
//情况1:兄弟结点为红色
if (w->color == RED) {
// 兄弟节点变成黑色
w->color = BLACK;
// 父节点变成红色
x->parent->color = RED;
// 父节点做右旋
rbtree_right_rotate(T, x->parent);
//将兄弟结点调整为父节点的左子树
w = x->parent->left;
}
// 情况2:兄弟节点是黑色的,且兄弟的左孩子和右孩子都是黑色
if ((w->left->color == BLACK) && (w->right->color == BLACK)) {
// 兄弟节点变成红色
w->color = RED;
// 轴心结点变为父节点
x = x->parent;
} else {
// 情况3:x的兄弟结点是黑色的,兄弟的左孩子是黑色,右孩子是红色
if (w->left->color == BLACK) {
//将右孩子变黑
w->right->color = BLACK;
//将兄弟节点变红
w->color = RED;
//对兄弟结点左旋
rbtree_left_rotate(T, w);
//将兄弟结点调整为父节点的左子树
w = x->parent->left;
}
// 情况4:x的兄弟结点是黑色的,兄弟的左孩子是红色,右孩子是黑色
// 将兄弟节点换成父节点的颜色
w->color = x->parent->color;
// 把父节点和兄弟节点的左孩子变黑
x->parent->color = BLACK;
w->left->color = BLACK;
// 对父节点做右旋
rbtree_right_rotate(T, x->parent);
//将轴心结点调整为根结点
x = T->root;
}
}
}
// 继承节点变为黑色,为了弥补失去的黑高
x->color = BLACK;
}
红黑树的遍历、查询、测试
rbtree_node *rbtree_search(rbtree *T, KEY_TYPE key) {
rbtree_node *node = T->root;
while (node != T->nil) {
if (key < node->key) {
node = node->left;
} else if (key > node->key) {
node = node->right;
} else {
return node;
}
}
return T->nil;
}
void rbtree_traversal(rbtree *T, rbtree_node *node) {
if (node != T->nil) {
rbtree_traversal(T, node->left);
printf("key:%d, color:%d\n", node->key, node->color);
rbtree_traversal(T, node->right);
}
}
int main() {
int keyArray[20] = {24, 25, 13, 35, 23, 26, 67, 47, 38, 98, 20, 19, 17, 49, 12, 21, 9, 18, 14, 15};
rbtree *T = (rbtree *) malloc(sizeof(rbtree));
if (T == NULL) {
printf("malloc failed\n");
return -1;
}
T->nil = (rbtree_node *) malloc(sizeof(rbtree_node));
T->nil->color = BLACK;
T->root = T->nil;
rbtree_node *node = T->nil;
int i = 0;
for (i = 0; i < 20; i++) {
node = (rbtree_node *) malloc(sizeof(rbtree_node));
node->key = keyArray[i];
node->value = NULL;
rbtree_insert(T, node);
}
rbtree_traversal(T, T->root);
printf("----------------------------------------\n");
for (i = 0; i < 20; i++) {
rbtree_node *node = rbtree_search(T, keyArray[i]);
rbtree_node *cur = rbtree_delete(T, node);
free(cur);
rbtree_traversal(T, T->root);
printf("----------------------------------------\n");
}
}