[数据结构与算法]leetcode 462. Minimum Moves to Equal Array Elements II （使数组元素相等的最小move数II）

Given an integer array nums of size n, return the minimum number of moves required to make all array elements equal.

In one move, you can increment or decrement an element of the array by 1.

Test cases are designed so that the answer will fit in a 32-bit integer.

Example 1:

Input: nums = [1,2,3]
Output: 2
Explanation:
Only two moves are needed (remember each move increments or decrements one element):
[1,2,3] => [2,2,3] => [2,2,2]
Example 2:

Input: nums = [1,10,2,9]
Output: 16

给一个数组nums，让用最小的move数使nums里面的元素全部相等。
一个move指的是对元素+1或-1。

思路：

先假设一个1~10连续数字的情形，假设1～10都向某个数字x靠拢，就是如下：

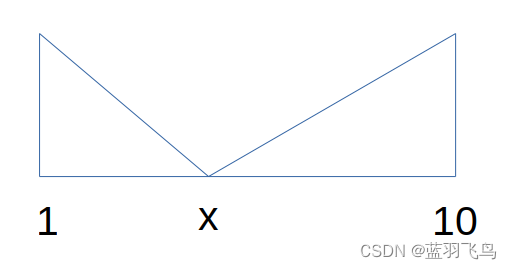
因为假设的是连续数字，所以需要的move数就是两个三角形的面积和，
0.5 * (x-1) * (x-1) + 0.5 * (10-x) * (10-x) = x² - 11x + 50.5

它是个凸函数，在导数为0的地方取最小值，于是在中位数的地方取最小值。

同样的，本题的最小move数也是向中位数靠拢。
所以要先把数组nums排序。

可以用一个loop遍历nums中的每个元素，move为每个元素与中位数之差的和。

但是可以发现，假设中位数是x,
每一步的move数为(x - nums[i]) + (nums[n-1-i] - x) = nums[n-1-i] - nums[i]
与中位数具体是多少无关。

于是变成了双指针。

public int minMoves2(int[] nums) {
    int n = nums.length;
    int left = 0;
    int right = n - 1;
    int res = 0;
    
    Arrays.sort(nums);
    
    while(left < right) {
        res += nums[right] - nums[left];
        left ++;
        right --;
    }
    return res;
}

参考链接