本篇博客一一详细介绍了线性表的两种实现方式,以及对应的c语言代码,并通过图片的方式解释代码,并对比两种实现方式的优缺点,最后以几道算法题进行总结和归纳。
目录
1. 线性表的定义
线性表是具有n个相同特性的数据元素的有限序列。线性表是一种实际中广泛使用的数据结构,常见的线性表有顺序表、链表、栈、队列、字符串等等。
其中n为表长,当 n = 0 时,线性表为空表。所以归纳总结,线性表具有以下特点:
- 表中的元素个数有限。
- 表中元素是按照一定的先后次序进行排序的,逻辑上是顺序的。
- 表中的元素都是同一种类型,具有相同的特性。
- 除了表头元素和表尾元素,每个元素都仅有一个前驱和一个后继。
2. 线性表的顺序表示
2.1 顺序表的定义
线性表的顺序存储又称顺序表,顺序表是用一段物理地址连续的存储单元,使得逻辑上相邻的两个元素物理位置上也相邻。一般采用数组存储。
顺序表可以分为两种:
- 静态顺序表:使用固定长度的数组进行存储元素
- 动态顺序表:使用动态开辟的数组进行存储元素
2.1.1 静态顺序表的图解和代码实现
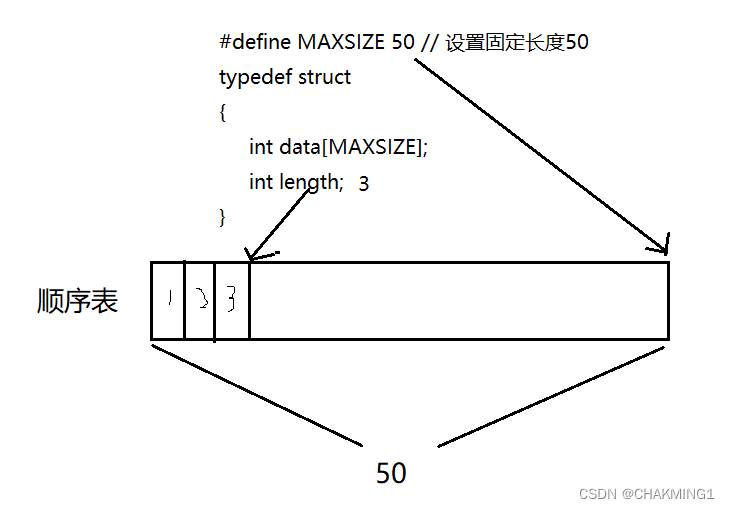
#define MAXSIZE 50
#define int SLDataType;
typedef struct
{
SLDataType array[MAXSIZE];
size_t size; // size_t 是一种无符号整型
}SeqList;?这是一种通过预先分配好的大小,这种实现方式实现起来比较简单,只需要一个一维数组,在创建时提前分配相应的大小,但同样会带来一些问题,一旦空间存储满之后,再加入新的元素就会导致溢出,且这种实现方式是无法进行扩容的,所以就引出了动态顺序表。
2.1.2 动态顺序表的代码实现
动态顺序表是通过malloc函数在堆区开辟一块连续分配的存储空间,在数据存储满之后,会重新在内存找另一块更大的空间,将原来的数据进行搬移到新空间里面,从而实现了扩容的操作,那么就不需要提前分配好多大的空间。
typedef int SLDateType;
typedef struct SeqList
{
SLDateType* a; // 动态开辟的数组
size_t size; // 当前元素的个数
size_t capacity; // size_t = unsigned int 容量
}SeqList;基本操作:
// 对数据的管理:增删查改
// 顺序表初始化
void SeqListInit(SeqList* ps);
// 顺序表的摧毁
void SeqListDestory(SeqList* ps);
// 打印顺序表
void SeqListPrint(SeqList* ps);
// 顺序表的尾插入元素
void SeqListPushBack(SeqList* ps, SLDateType x);
// 顺序表的头插入元素
void SeqListPushFront(SeqList* ps, SLDateType x);
// 顺序表的尾删除元素
void SeqListPopBack(SeqList* ps);
// 顺序表的头删除元素
void SeqListPopFront(SeqList* ps);
// 顺序表查找
int SeqListFind(SeqList* ps, SLDateType x);
// 顺序表在pos位置插入x
void SeqListInsert(SeqList* ps, size_t pos, SLDateType x);
// 顺序表删除pos位置的值
void SeqListErase(SeqList* ps, size_t pos);(1) 初始化
void SeqListInit(SeqList* ps)
{
assert(ps != NULL);
ps->a = NULL;
ps->size = ps->capacity = 0;
}这一步并不难,只需要将顺序表中的指针指向NULL,当前的大小和容器置为0即可。
(2)插入操作
插入操作有三种,一种是尾插,一种是头插,一种是指定位置插入,这里用指定位置插入为例:
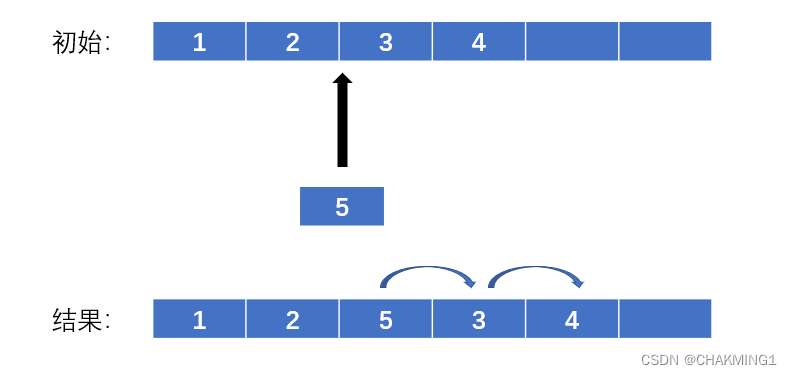
?假设我们已有一个线性表,将5插入到2和3之间,那么这个时候,为了保证数据的连续性,会从最后一个元素开始依次往前,将每个元素往后放。
void SqCheckCapacity(SeqList *ps)
{
assert(ps != NULL);
// 检查容量是否已满
if (ps->size == ps->capacity)
{
int newCapacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;
SeqList* tmp = (SeqList*)realloc(ps->a, newCapacity *sizeof (SeqList));
if (tmp == NULL) {
perror("realloc");
return;
}
ps->a = tmp;
ps->capacity = newCapacity;
}
}
// 指定位置插入
void SeqListInsert(SeqList* ps, size_t pos, SLDateType x)
{
assert(ps != NULL);
assert(pos >= 0 && pos <= ps->size);
SqCheckCapacity(ps);
for (int i = ps->size; i > pos; i--)
{
ps->a[i] = ps->a[i-1];
}
ps->a[pos] = x;
ps->size++;
}
// 尾插
void SeqListPushBack(SeqList* ps, SLDateType x)
{
// 方法1
assert(ps != NULL);
SqCheckCapacity(ps);
ps->a[ps->size++] = x;
// 复用insert操作
SeqListInsert(ps, ps->size, x);
}
// 头插
void SeqListPushFront(SeqList* ps, SLDateType x)
{
// 方法1
assert(ps != NULL);
SqCheckCapacity(ps);
for (int i = ps->size-1; i >= 0; i--)
{
ps->a[i+1] = ps->a[i];
}
ps->a[0] = x;
ps->size++;
// 服用insert操作
SeqListInsert(ps, 0, x);
}由于这是动态数组,所以再每次进行插入的时候都要检查一下容量是否已满,若已满,则进行扩容,若当前数组是一个空指针,那么就会默认开辟4个大小给当前数组。
(3) 删除操作
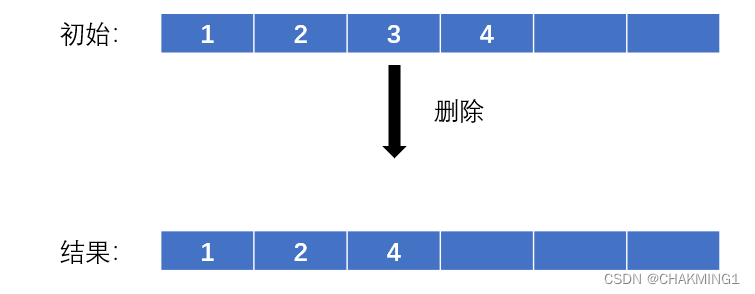
?同样删除元素,只需要当前要删除的元素后面的元素依次往前移即可。
// 指定位置删除
void SeqListErase(SeqList* ps, size_t pos)
{
assert(ps != NULL);
assert(pos >= 0 && pos < ps->size);
for (int i = pos; i < ps->size - 1; i++)
{
ps->a[i] = ps->a[i + 1];
}
ps->size--;
}
// 头删
void SeqListPopFront(SeqList* ps)
{
// 方法1
assert(ps != NULL);
assert(ps->size > 0);
for (int i = 0; i < ps->size-1; i++)
{
ps->a[i] = ps->a[i + 1];
}
ps->size--;
// 复用erase操作
SeqListErase(ps, 0);
}
// 尾删
void SeqListPopBack(SeqList* ps)
{
// 方法1
assert(ps != NULL);
assert(ps->size > 0);
ps->size--;
// 复用erase操作
SeqListErase(ps, ps->size - 1);
}由此可见,顺序表的插入和删除操作的时间主要是消耗再移动元素上,而移动元素取决于要插入和删除的位置,如果是在尾部插入和删除元素,时间复杂度为O(1),如果是在头部进行插入和删除元素,时间复杂度为O(n),如果是在中间插入和删除元素,平均时间复杂度为O(n)。
(4)查找操作
// 查找
int SeqListFind(SeqList* ps, SLDateType x)
{
assert(ps != NULL);
for (int i = 0; i < ps->size; i++)
{
if (ps->a[i] == x)
return i;
}
return -1;
}遍历一遍顺序表,找到与x值相同的下标,并返回,如果找不到,则返回-1。
最好情况:查找的元素在表头,仅需要比较一次,时间复杂度为O(1)。
最坏情况:查找的元素在表尾或者不存在,时间复杂度为O(n)。
平均情况:时间复杂度为O(n)。
(5)摧毁操作
// 销毁线性表
void SeqListDestory(SeqList* ps)
{
assert(ps != NULL);
if (ps->a)
{
free(ps->a);
ps->a = NULL;
ps->size = ps->capacity = 0;
}
}摧毁操作是必须的,因为我们在初始化的时候,会在堆区开辟一段空间,而这个空间如果不进行释放,会造成内存泄漏,所以摧毁函数就是用free函数将顺序表释放。
2.1.3 顺序表相关leetcode题目
1. 移除元素?OJ链接
?题目:原地移除数组中val值的元素,不能使用额外的空间,返回移除元素后新数组的大小。
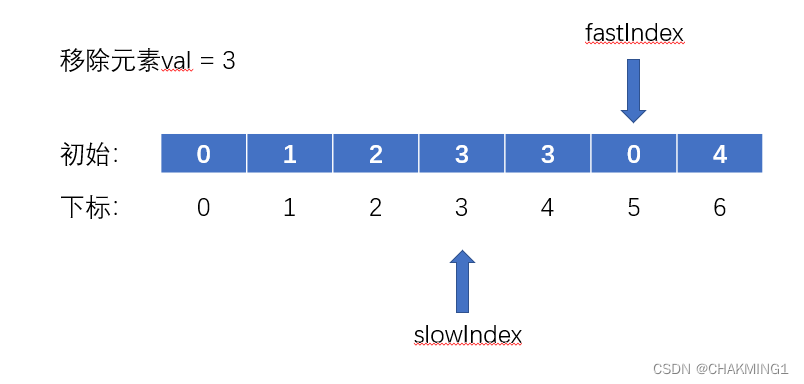
?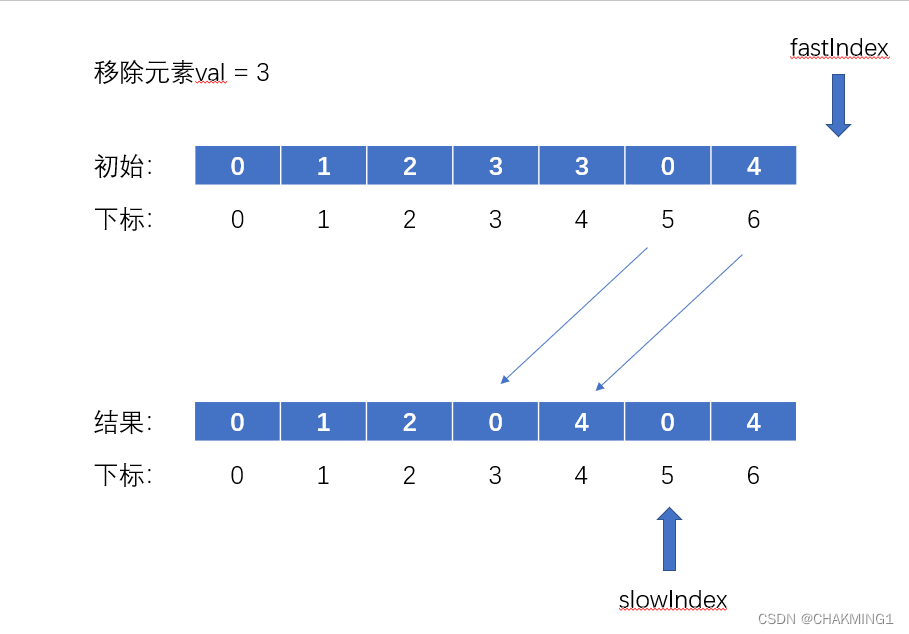
int removeElement(int* nums, int numsSize, int val){
int slowIndex = 0;
for(int fastIndex = 0;fastIndex<numsSize;fastIndex++)
{
if(val != nums[fastIndex])
nums[slowIndex++] = nums[fastIndex];
}
return slowIndex;
}2.1.4 顺序表所存在的问题
- 中间和头部的插入和删除效率低
- 增容需要扩充新空间,并且需要做搬移操作,同样也会造成一定的消耗
- 增容一般是两倍扩充,有可能会造成一定的空间浪费。
3. 线性表的链式表示
3.1 链表的定义
链表是线性表的链式存储,它是通过一组任意的存储单元来存储线性表的中的数据元素。为了建立数据元素之间的线性关系,对于每个链表结点,除了存放元素自身的信息之外,还存放一个指向下一个结点的指针。

链表可以解决顺序表需要大量存储单元的缺点,但单链表在存储结点元素的值之外,额外存储了一个指针域,并且链表的元素离散得分布在存储空间中,所以单链表是非随机存取的存储结构。
3.1.1?链表的分类
1. 单链表或者双链表

?
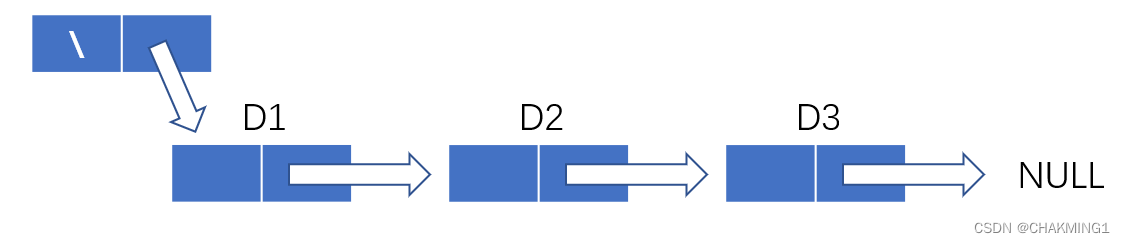
2. 带头链表或者不带头链表
?
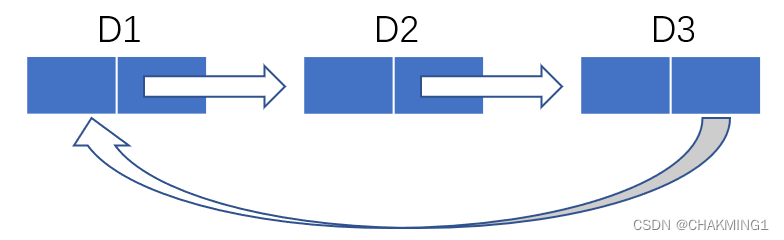
3. 循环链表或者非循环链表
?
通过上面三种分类可以组合成八种链表结构,但是最为常用的就是不带头的单链表以及带头双向循环链表。
- 不带头的单链表:结构简单,一般不会用来存储数据。更多的是用在其他数据结构的子结构中。
- 带头双向循环链表:结构复杂,一般是用来存储数据。实际中使用的链表都是以这个为主。
3.1.2?链表的实现?
(1)单链表

// 1. 不带头 + 单向 + 非循环链表的结构以及基本操作
// 结构
typedef int SLTDataType;
typedef struct SListNode
{
SLTDataType data; // 存储结点元素的值
struct SListNode* next; // 存储指向下一个结点的指针域
}SLTNode;
// 操作
SLTNode* BuySListNode(SLTDataType x); // 创建新结点
void SListPrint(SLTNode* phead); // 打印元素
void SListPushBack(SLTNode** pphead, SLTDataType x); // 尾插
void SListPushFront(SLTNode** pphead, SLTDataType x); // 头插
void SListPopBack(SLTNode** pphead); // 尾删
void SListPopFront(SLTNode** pphead); // 头删
SLTNode* SListFind(SLTNode* phead, SLTDataType x); // 查找元素
// 在pos位置之前插入
void SListInsert(SLTNode** pphead, SLTNode* pos, SLTDataType x);
// 删除pos位置的值
void SListErase(SLTNode** pphead, SLTNode* pos);基本操作具体实现方式:
// 动态申请一个结点
SLTNode* BuySListNode(SLTDataType x)
{
SLTNode* newnode = (SLTNode*)malloc(sizeof(SLTNode));
assert(newnode);
newnode->data = x;
newnode->next = NULL;
return newnode;
}上面的操作是从堆区开辟一小块空间,这块空间就相当于链表的一个结点,结点里面有元素的值和存储下一个结点的指针,元素的值,我们可以通过传参进去,由于不清楚元素的下一个结点,所以这里置为空。
// 尾插
void SListPushBack(SLTNode** pphead, SLTDataType x)
{
SLTNode* newnode = BuySListNode(x);
if (*pphead == NULL)
{
*pphead = newnode;
}
else
{
// 找尾节点
SLTNode* tail = *pphead;
while (tail->next != NULL)
{
tail = tail->next;
}
tail->next = newnode;
}
}
// 头插
void SListPushFront(SLTNode** pphead, SLTDataType x)
{
SLTNode* newnode = BuySListNode(x);
newnode->next = *pphead;
*pphead = newnode;
}// 尾删
void SListPopBack(SLTNode** pphead)
{
assert(*pphead);
// 1、只有一个节点
// 2、多个节点
if ((*pphead)->next == NULL)
{
free(*pphead);
*pphead = NULL;
}
else
{
/*SLTNode* tailPrev = NULL;
SLTNode* tail = *pphead;
while (tail->next != NULL)
{
tailPrev = tail;
tail = tail->next;
}
free(tail);
tailPrev->next = NULL;*/
SLTNode* tail = *pphead;
while (tail->next->next != NULL)
{
tail = tail->next;
}
free(tail->next);
tail->next = NULL;
}
}
// 头删
void SListPopFront(SLTNode** pphead)
{
assert(*pphead != NULL);
SLTNode* next = (*pphead)->next;
free(*pphead);
*pphead = next;
}
// 单链表查找,找出对应值,并返回结点
SLTNode* SListFind(SLTNode* phead, SLTDataType x)
{
SLTNode* cur = phead;
while (cur)
{
if (cur->data == x)
return cur;
cur = cur->next;
}
return NULL;
}
// 是在pos后插入
void SListInsert(SLTNode** pphead, SLTNode* pos, SLTDataType x)
{
// 头插
if (pos == *pphead)
{
SListPushFront(pphead, x);
}
else
{
SLTNode *newNode = BuySListNode(x);
newNode->next = pos->next;
pos->next = newNode;
}
}
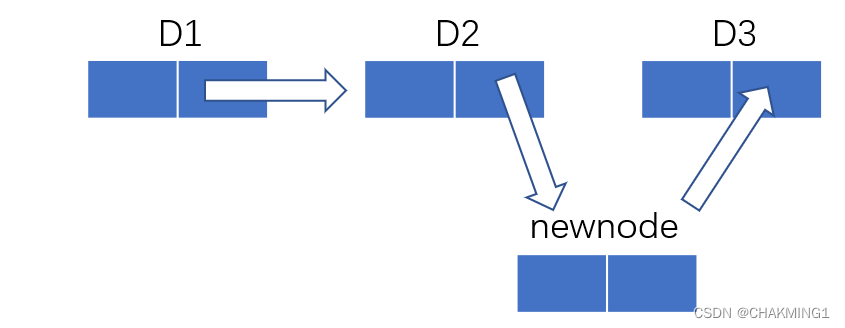
这里并没有给出删除pos位置的结点,这是因为这个操作并没有多大的意义,因为在单链表中删除一个结点,必须知道前一个结点的位置,但是我们只知道当前结点的位置,如果需要删除,就要从头开始去找,这样就会造成时间复杂度达到O(n)这个级别。
(2)带头双向循环链表
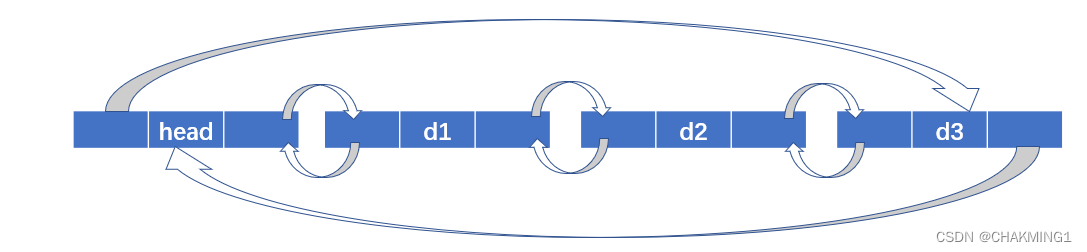
// 2. 带头双向循环链表
// 结构
typedef int LTDataType;
typedef struct ListNode
{
struct ListNode* next; // 指向下一个结点
struct ListNode* prev; // 指向前一个结点
LTDataType data;
}LTNode;
// 基本操作
LTNode* ListInit();
void ListPrint(LTNode* phead);
void ListPushBack(LTNode* phead, LTDataType x);
void ListPushFront(LTNode* phead, LTDataType x);
void ListPopBack(LTNode* phead);
void ListPopFront(LTNode* phead);
bool ListEmpty(LTNode* phead);
// 在pos位置之前插入x
void ListInsert(LTNode* pos, LTDataType x);
// 删除pos位置的节点
void ListErase(LTNode* pos);
?基本操作实现具体方式
// 创建一个新结点
LTNode* BuyListNode(LTDataType x)
{
LTNode* node = (LTNode*)malloc(sizeof(LTNode));
if (node == NULL)
{
perror("malloc fail");
exit(-1);
}
node->data = x;
node->next = NULL;
node->prev = NULL;
return node;
}
// 初始化列表,创建一个虚拟头结点,并赋值-1,实际上这个-1无任何意义
LTNode* ListInit()
{
LTNode* phead = BuyListNode(-1);
phead->next = phead;
phead->prev = phead;
return phead;
}// 尾插
void ListPushBack(LTNode* phead, LTDataType x)
{
assert(phead);
LTNode* newnode = BuyListNode(x);
LTNode* tail = phead->prev;
tail->next = newnode;
newnode->prev = tail;
newnode->next = phead;
phead->prev = newnode;
}
// 头插
void ListPushFront(LTNode* phead, LTDataType x)
{
assert(phead);
LTNode* newnode = BuyListNode(x);
LTNode* next = phead->next;
// phead newnode next
phead->next = newnode;
newnode->prev = phead;
newnode->next = next;
next->prev = newnode;
}void ListPopBack(LTNode* phead)
{
assert(phead);
assert(phead->next != phead);
LTNode* tail = phead->prev;
LTNode* tailPrev = tail->prev;
free(tail);
tailPrev->next = phead;
phead->prev = tailPrev;
}
void ListPopFront(LTNode* phead)
{
assert(phead);
assert(phead->next != phead);
phead->next->next->prev = phead;
phead->next = phead->next->next;
}// 在pos位置之前插入x
void ListInsert(LTNode* pos, LTDataType x)
{
assert(pos);
LTNode* prev = pos->prev;
LTNode* newnode = BuyListNode(x);
// prve newnode pos
prev->next = newnode;
newnode->prev = prev;
newnode->next = pos;
pos->prev = newnode;
}
// 删除pos位置的节点
void ListErase(LTNode* pos)
{
assert(pos);
LTNode* prev = pos->prev;
LTNode* next = pos->next;
prev->next = next;
next->prev = prev;
free(pos);
}以上是任意位置插入和删除的实现方式,具体讲解如何实现代码,首先,我们知道在单链表中要插入一个元素,肯定要知道这个结点的前一个结点,但是单链表只有指向后继结点的指针,所以我们没有办法实现在链表前插入元素,但是在双向链表中就可以实现这种操作。这个时候修改对应的指针域就可以了,这里存储了该结点的前一个结点,是防止后续插入的过程中顺序问题导致结点的前一个结点与当前结点的链接断掉的问题。
删除指定位置的元素,这个操作在单链表中是没有多大意义的,因为我们并不知道当前结点的前一个结点,但是在双向链表,我们可以找到前一个结点的位置,这个时候就只需要修改指针即可。
3.1.3?链表相关的LeetCode题目
反转该链表并输出反转后链表的头节点,我们发现单链表是指向后继结点的元素,如果将每个指针域的指针指向前一个元素,就实现了反转操作。

?
?
struct ListNode* reverseList(struct ListNode* head){
struct ListNode *temp; // 保存cur的下一个结点
struct ListNode *cur = head;
struct ListNode *pre = NULL; // pre是指向当前结点的前一个结点
while(cur)
{
temp = cur->next;
cur->next = pre; // 反转操作
// 更新cur和pre
pre = cur;
cur = temp;
}
// cur 指向空,pre指向原链表最后一个结点,故作为最终的头结点
return pre;
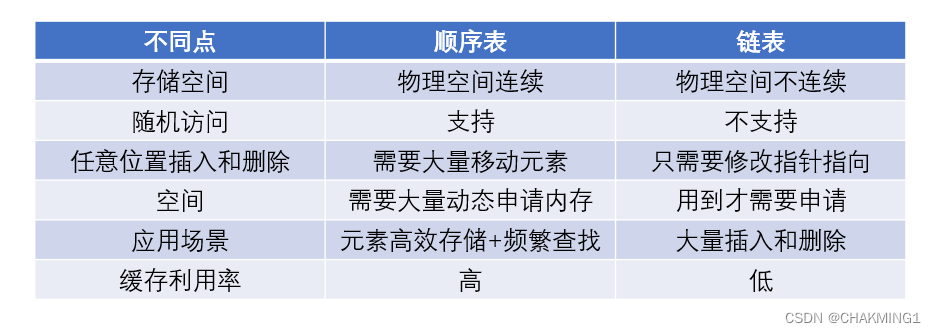
}4. 顺序表与链表的比较