?? 已经两个月没有更博客了,今天闲来无事就来谈谈双向链表。(双向链表也是看了许多优秀的博主之后才学会的TAT)
? 1:双向链表的介绍
?? ,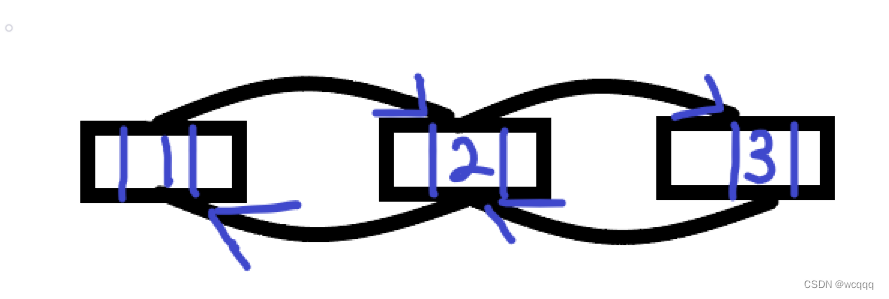
?跟单链表一样,双向链表的每个节点都有指针域和数据域。但相较于普通的单链表,双向链表多了前驱指针。每个节点都有它的值data,一个指向后面节点的指针,一个指向前面节点的指针。(这个应该是好理解的,这个可以看图就明白了)接下来就介绍下双向链表的定义和它的基本操作。
2:双向链表的节点定义
其实就是单链表节点的基础上在多一个前驱指针,这里不多解释,直接上代码。
struct node
{
node *next; //!后继
node *pre; //!前继
int data;
node(int d) : next(0), pre(0), data(d) {}
};3:双向链表类的定义
跟单链表类的定义方式一样。
class List
{
node *first, *last;
int length;
public:
List() : first(0), last(0), length(0) {}//构造函数
//各类函数
};4:双向链表的插入
这个我个人觉得会比单链表的插入会复杂一点
1:一开始的状态
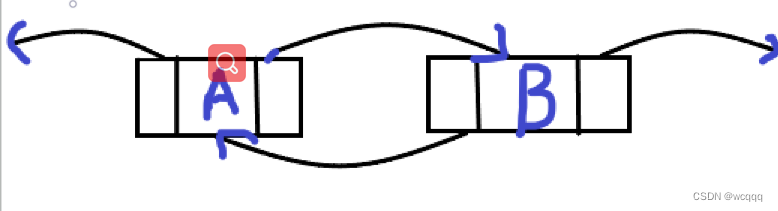
?2:加入新节点
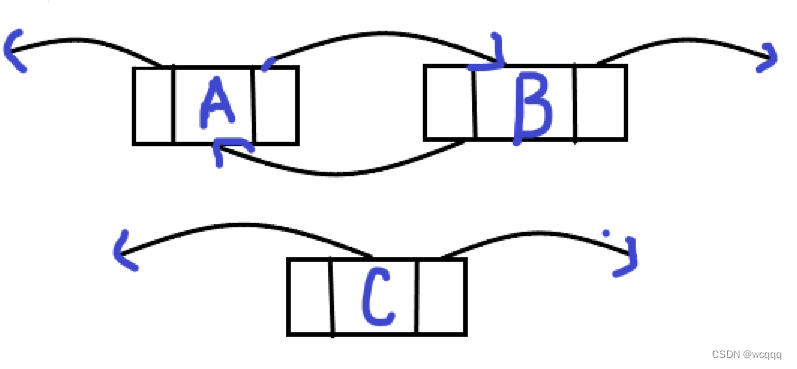
?3:把C的前驱指针指向B
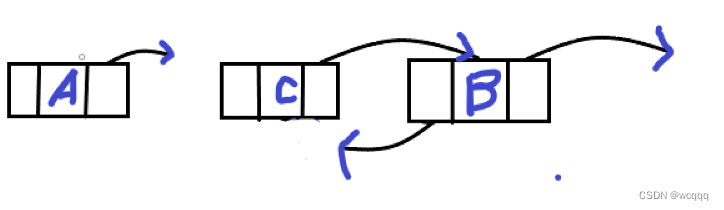
4: 把A的前驱指针指向C
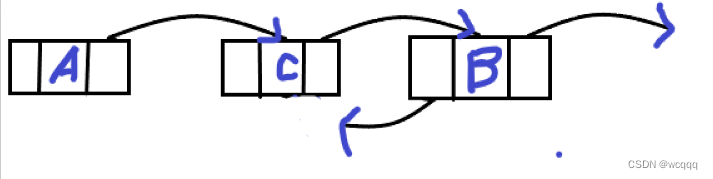
?5:把B的前驱指针指向C,把C的指针指向A
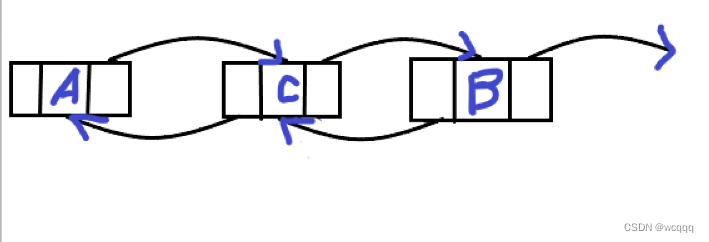
?代码如下
void inseart(node *ptr, int d) //!插入函数
{
if (!Find(ptr))
return;
node *p = new node(d);
p->next = ptr->next;
ptr->next = p;
p->next->pre = p;
p->pre = ptr;
length++;
}5:双向链表的删除
1:找到要删除的节点(这里删除C节点)
直接从头到尾遍历一遍或者从尾到头遍历都可以
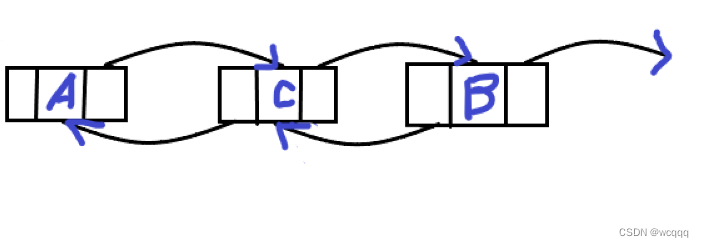
?2:把A的后驱指针指向B,B的前驱指针指向A
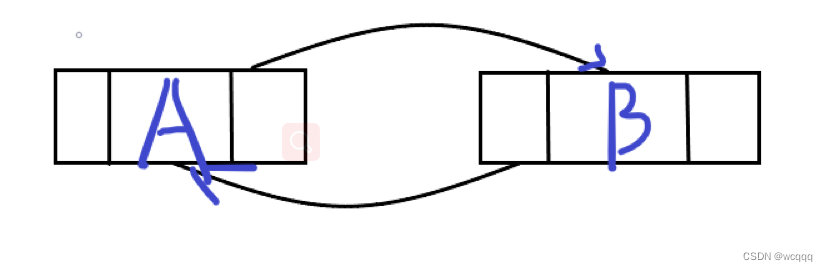
3:deleteC节点
代码如下
void erase(int d)
{
if (!find(d))
return;
node *ptr;
for (node *p = first; p; p = p->next)
{
if (p->data == d)
{
ptr = p;
break;
}
}
node *p = ptr->pre;
node *pp = ptr->next;
p->next = pp;
pp->pre = p;
delete ptr;
length--;
}6:双向链表的查找
跟单链表一样,就是一个个指针通过next指针一个个查找过来
bool Find(node *ptr)
{
for (node *p = first; p; p = p->next)
{
if (p->data == ptr->data)
return true;
}
return false;
}7:双向链表的输出
相较于单链表有两种方式输出
1:顺序输出
通过next指针一个个输出指针的data的值
void print_front()
{ //!顺序输出
for (node *p = first; p; p = p->next)
{
cout << p->data << " ";
}
cout << endl;
}2:倒序输出
通过pre指针进行倒序输出
void print_last()
{ //!倒序输出
for (node *p = last; p; p = p->pre)
{
cout << p->data << " ";
}
cout << endl;
}8:总结
?? 说实话,双向链表其实还是很简单的。当初写C++课设的时候,本来想用的,但是怕出错,就没敢用了。好久没写博客了,写的确实有点拉胯了。但希望大家能从我的博客中学到新东西。
9:完整代码(方便大家自行调试)
#include <bits/stdc++.h>
using namespace std;
struct node
{
node *next; //!后继
node *pre; //!前继
int data;
node(int d) : next(0), pre(0), data(d) {}
};
class List
{
node *first, *last;
int length;
public:
List() : first(0), last(0), length(0) {}
void push_back(int d)
{
node *p = new node(d);
if (first == 0)
{
first = last = p;
length++;
return;
}
last->next = p;
p->pre = last;
last = p;
length++;
}
void inseart(node *ptr, int d) //!插入函数
{
if (!Find(ptr))
return;
node *p = new node(d);
p->next = ptr->next;
ptr->next = p;
p->next->pre = p;
p->pre = ptr;
length++;
}
bool Find(node *ptr)
{
for (node *p = first; p; p = p->next)
{
if (p->data == ptr->data)
return true;
}
return false;
}
bool find(int d)
{
for (node *p = first; p; p = p->next)
{
if (p->data == d)
return true;
}
return false;
}
void erase(int d)
{
if (!find(d))
return;
node *ptr;
for (node *p = first; p; p = p->next)
{
if (p->data == d)
{
ptr = p;
break;
}
}
node *p = ptr->pre;
node *pp = ptr->next;
p->next = pp;
pp->pre = p;
delete ptr;
length--;
}
void print_front()
{ //!顺序输出
for (node *p = first; p; p = p->next)
{
cout << p->data << " ";
}
cout << endl;
}
void print_last()
{ //!倒序输出
for (node *p = last; p; p = p->pre)
{
cout << p->data << " ";
}
cout << endl;
}
node *begin()
{
return first;
}
};
int main()
{
List L;
for (int i = 0; i < 9; ++i)
{
L.push_back(i);
}
L.print_front();
L.print_last();
L.erase(5);
L.print_front();
L.print_last();
int cnt = 1;
for (node *p = L.begin(); cnt <= 5; p = p->next)
{
// cout << p->data << endl;
L.inseart(p, cnt);
cnt++;
}
// cout << "Yes" << endl;
L.print_front();
L.print_last();
}