一、冒泡排序
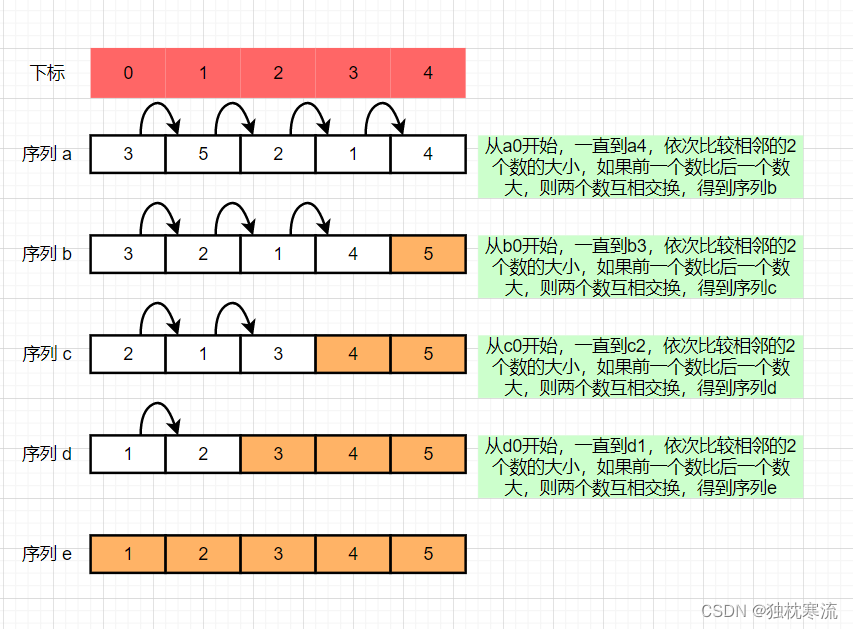
冒泡排序(Bubble Sort),它重复地走访过要排序的元素列,依次比较两个相邻的元素,如果顺序(如从大到小、首字母从Z到A)不对,就把它们交换过来。走访元素的工作是重复地进行,直到没有相邻元素需要交换,也就是说该元素列已经排序完成。
这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到元素列的顶端(升序或降序排列),就如同碳酸饮料中二氧化碳的气泡最终会上浮到顶端一样,故名“冒泡排序”。
排序思路示意图:
实现代码:
//C++版本
#include <iostream>
using namespace std;
template<typename T>
void bubble_sort(T *pArr, int len)
{
int i, j;
T temp;
for (i = len - 1; i > 0; i--)
{
for (j = 0; j < i; j++)
{
if (pArr[j] > pArr[j+1])
{
temp = pArr[j+1];
pArr[j+1] = pArr[j];
pArr[j] = temp;
}
}
}
}
int main()
{
int arr[] = {3,5,2,1,4};
int len = sizeof(arr)/sizeof(*arr);
int i;
cout << "---before bubble sort---" << endl;
for (i = 0; i < len; i++)
{
cout << arr[i] << " ";
}
cout << endl;
bubble_sort(arr, len);
cout << "---after bubble sort---" << endl;
for (i = 0; i < len; i++)
{
cout << arr[i] << " ";
}
cout << endl;
return 0;
}
运行结果:

时间复杂度
1.最优的情况:
待排序的元素列已经排好序了,那么就不用移动(Move)元素了,即Mmin = 0,由于外循环循环次数为n-1,那么内循环需要比较(compare)的次数为(n-1, n-2, …, 3, 2, 1),由等差数列求和 (1+n-1)(n-1)/2 = n(n-1)/2,即Cmin = n(n-1)/2,所以最优的情况,时间复杂度为:O(n2)
2.最坏的情况:
待排序的元素列反序了,那么就是比最优的情况,每次比较都要进行元素的交换,而且每次交换只有3步赋值运算,所以最坏的情况,时间复杂度为:3n(n-1)/2,即时间复杂度为:O(n2)
综上所述,冒泡排序的时间复杂度为:O(n2)
算法稳定性
冒泡排序就是将要排序的元素列,相邻的两个元素进行比较,如果前面的元素比后面的元素大,才会进行交换,而且如果两个元素相等,也不会进行交换,所以冒泡排序是一种稳定的排序算法。
空间复杂度
冒泡排序的辅助移动的变量空间只有一个临时变量(代码中的T temp),并且不会随着排序规模的扩大而变大,所以冒泡排序的空间复杂度为:O(1)
二、选择排序
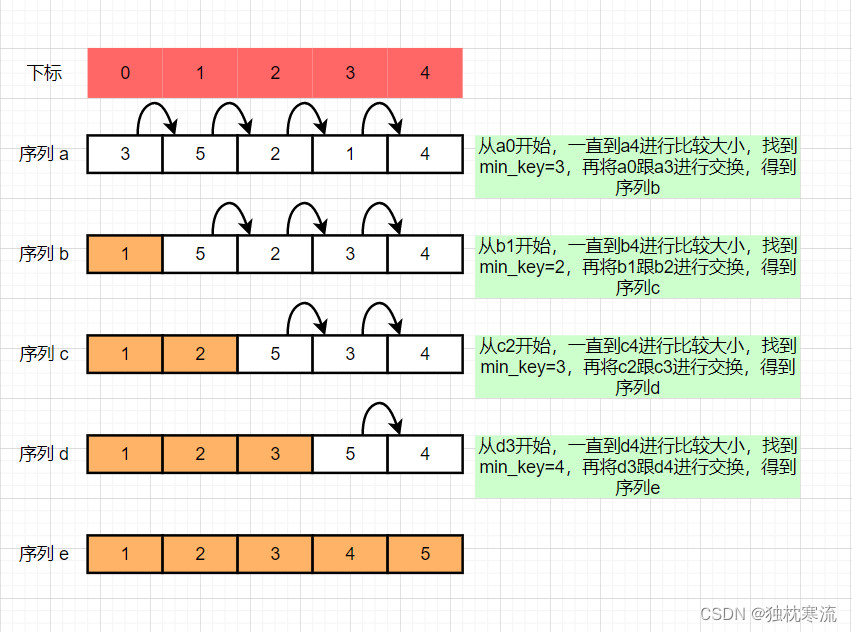
选择排序(Selection Sort),是一种简单直观的排序算法,它的工作原理是,从待排序的元素列中找到最小(大)的元素放在元素列中的起始位置,然后再从剩下的未排序的元素中找到最小(大)的元素,放在已排序的序列中,循环直到所有的未排序的元素个数为0为止。
排序思路示意图:
实现代码:
//C++版本
#include <iostream>
using namespace std;
template<typename T>
void select_sort(T *pArr, int len)
{
int i, j, min_key;
T temp;
for (int i = 0; i < len - 1; i++)
{
min_key = i;
for (j = i + 1; j < len; j++)
{
if (pArr[j] < pArr[min_key])
min_key = j;
}
if (min_key != i)
{
temp = pArr[min_key];
pArr[min_key] = pArr[i];
pArr[i] = temp;
}
}
}
int main()
{
int arr[] = {3,5,2,1,4};
int len = sizeof(arr)/sizeof(*arr);
int i;
cout << "---before select sort---" << endl;
for (i = 0; i < len; i++)
{
cout << arr[i] << " ";
}
cout << endl;
select_sort(arr, len);
cout << "---after select sort---" << endl;
for (i = 0; i < len; i++)
{
cout << arr[i] << " ";
}
cout << endl;
return 0;
}
运行结果:
时间复杂度
1.最优的情况:
待排序的元素列已经排好序了,那么就不用移动(Move)元素了,即Mmin = 0,由于外循环循环次数为n-1,那么内循环需要比较(compare)的次数为(n-1, n-2, …, 3, 2, 1),由等差数列求和 (1+n-1)(n-1)/2 = n(n-1)/2,即Cmin = n(n-1)/2,所以最优的情况,时间复杂度为:O(n2)
2.最坏的情况:
每一趟比较下来,都要进行移动一次,那么也就是说最坏的情况,算法需要移动n-1次,赋值运算需要进行3步,即Mmax = 3(n-1)。比较的次数跟待排序元素列的初始状态无关,所以,最大次数Cmax = n(n-1)/2,所以最坏的情况,时间复杂度为:O(n2)
综上所述,选择排序的时间复杂度为:O(n2)
算法稳定性
选择排序算法是不稳定的排序算法,因为每次都是在未排序的元素列中,找到最小的那个元素,放到已排序的元素列的末尾,可能会调换两个相等元素的先后位置,那么原序列中两个相等元素的先后顺序就破坏了,所以选择排序算法是不稳定的排序算法。比如{3,3,1,2},第一趟排序中,首位置的3和第3个位置的1进行互换,得到的{1,3,3,2},最开始的首位置的3和第2位置的3的先后位置就破坏了。
空间复杂度
选择排序辅助移动的变量空间只有两个临时变量(代码中的T temp和int min_key),并且不会随着排序规模的变大而变大,所以选择排序的空间复杂度为:O(1)
三、插入排序
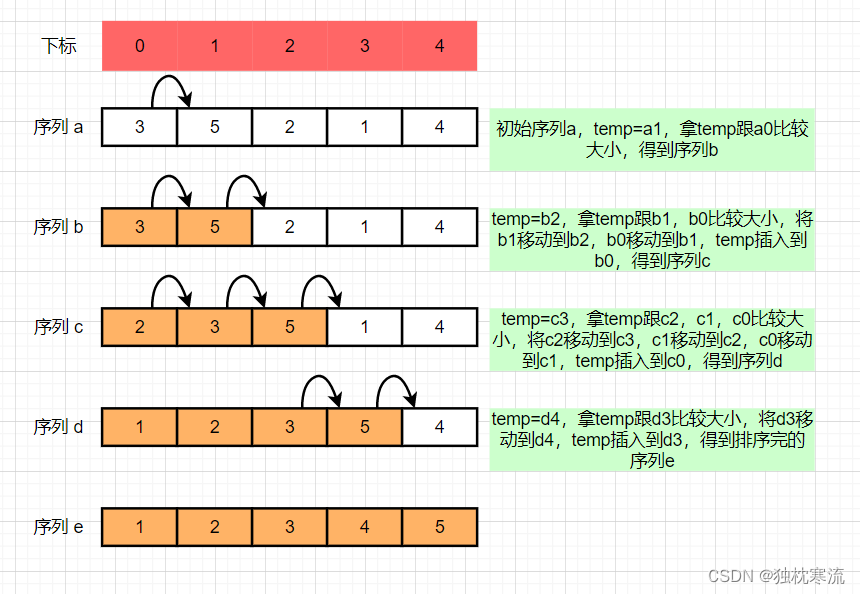
插入排序(Insertion Sort),一般也被称为直接插入排序。对于少量元素的排序,它是一个有效的算法。它的工作原理是,将一个元素插入到已经排好序的有序序列中,从而得到一个新的,记录数增加一个的有序序列。在其实现过程使用双层循环,外层循环对除了第一个元素之外的所有元素,内层循环对当前元素前面有序序列进行待插入位置查找,并进行移动,直到找到合适的位置进行插入操作。
排序思路示意图:
实现代码:
//C++版本
#include <iostream>
using namespace std;
template<typename T>
void insert_sort(T *pArr, int len)
{
int i, j, temp;
for (i = 1; i < len; i++)
{
temp = pArr[i];
for (j = i; j > 0 && temp < pArr[j-1]; j--)
{
pArr[j] = pArr[j-1];
}
pArr[j] = temp; /*1:当比较至少需要将前面一项进行移动时,上面的内循环for已经执行了j--,
所以这个下标是j,而不是j-1
2:当比较不需要移动时,上面的内循环for是没有执行j--,所以这时下标是j=i
*/
}
}
int main()
{
int arr[] = {3,5,2,1,4};
int len = sizeof(arr)/sizeof(*arr);
int i;
cout << "---before insert sort---" << endl;
for (i = 0; i < len; i++)
{
cout << arr[i] << " ";
}
cout << endl;
insert_sort(arr, len);
cout << "---after insert sort---" << endl;
for (i = 0; i < len; i++)
{
cout << arr[i] << " ";
}
cout << endl;
return 0;
}
运行结果:

时间复杂度
1.最优的情况:
待排序的元素列已经是顺序排好序的,那么最小移动(Move)次数:Mmin = 0;比较(compare)次数为n-1次,即Cmin = n-1,所以最优的情况,插入排序的时间复杂度为:O(n)
2.最坏的情况:
待排序的元素列是逆序的,那么最大移动(Move)次数:Mmax = (1+2+…+n-2+n-1),等差数列求和得:Mmax = n(n-1)/2。最大比较(compare)次数:Cmax = (1+2+…+n-2+n-1),等差数列求和得:Mmax = n(n-1)/2。所以Mmax + Cmax = n(n-1)/2 + n(n-1)/2 = n(n-1),所以最差的情况,插入排序的时间复杂度为:O(n2)
算法稳定性
插入排序不会调换两个相同的元素的先后顺序,所以插入排序是一种稳定的排序算法。
空间复杂度
插入排序辅助移动的变量空间只有一个临时变量(即代码中的 T temp),并且也不会随着排序规模的变大而变大,所以插入排序的空间复杂度为:O(1)
四、希尔排序
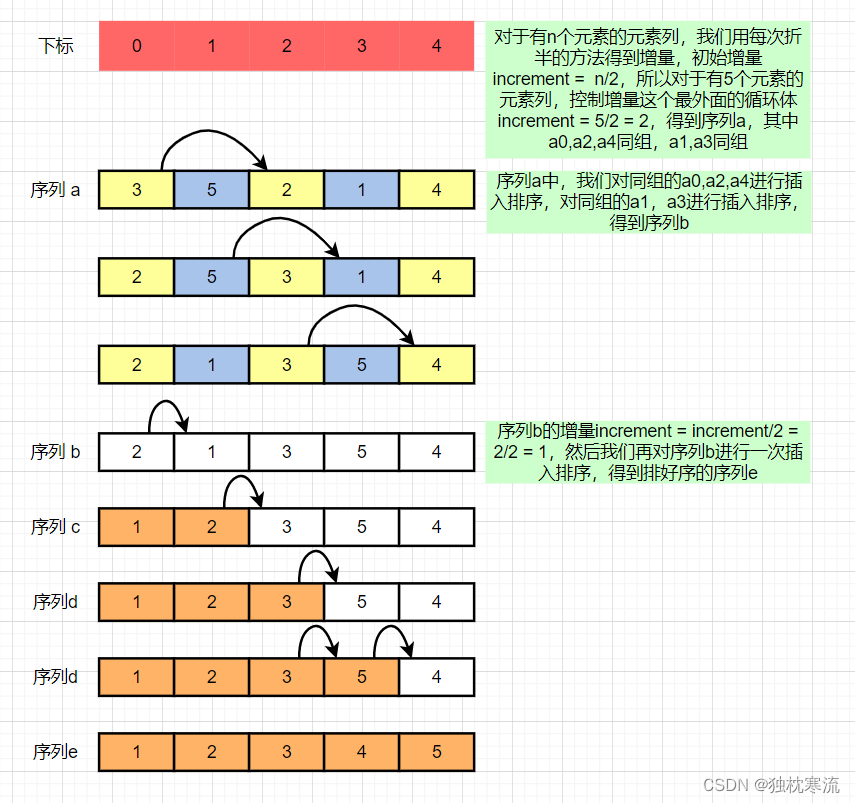
希尔排序(Shell Sort),是插入排序的一种,又称为“缩小增量排序”(Diminishing Increment Sort),是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因 D.L.Shell 于 1959 年提出而得名。它的工作原理是将待排序的元素列的下标按照一定的规则得到增量,然后依据该增量对待排序的元素列进行分组,得到该增量个子序列,对每个子序列进行插入排序。然后按照一定的规则逐渐减少增量,循环以上操作,直到增量为1时,整个元素列恰好被分成了一组,然后对该组进行最后一次插入排序,得到的元素列即为排序好的元素列。
排序思路示意图:
实现代码:
//C++版本
#include <iostream>
using namespace std;
template<typename T>
void shell_sort(T *pArr, int len)
{
int i,j;
T temp;
int increment = len; // 增量
while(increment > 1)
{
increment = increment/2;
for (i = 0; i < len - increment; i++)
{
temp = pArr[i + increment];
for (j = i + increment; j > 0 && temp < pArr[j-increment]; j -= increment)
{
pArr[j] = pArr[j - increment];
}
pArr[j] = temp;
}
}
}
int main()
{
int arr[] = {3,5,2,1,4};
int len = sizeof(arr)/sizeof(*arr);
int i;
cout << "---before shell sort---" << endl;
for (i = 0; i < len; i++)
{
cout << arr[i] << " ";
}
cout << endl;
shell_sort(arr, len);
cout << "---after shell sort---" << endl;
for (i = 0; i < len; i++)
{
cout << arr[i] << " ";
}
cout << endl;
return 0;
}
运行结果:

时间复杂度
这个依赖于增量序列的选择,而且怎样的增量序列对于希尔排序来说,是最优的选择,目前好像还是没有一个确定的定论,那么我们就记住希尔排序的时间复杂度为:O(n(1.3-2)),平均时间复杂度为:O(n1.3)
下面这段说明摘抄自百度百科
1.增量序列的选择
希尔排序的执行时间依赖于增量序列。
好的增量序列的共同特征:
① 最后一个增量必须为1;
② 应该尽量避免序列中的值(尤其是相邻的值)互为倍数的情况。
有人通过大量的实验,给出了较好的结果:当n较大时,比较和移动的次数约在n1.25到(1.6n)1.25之间。
2.希尔排序的时间性能优于直接插入排序
希尔排序的时间性能优于直接插入排序的原因:
①当元素列基本有序时直接插入排序所需的比较和移动次数均较少。
②当n值较小时,n和n2的差别也较小,即直接插入排序的最好时间复杂度O(n)和最坏时间复杂度0(n2)差别不大。
③在希尔排序开始时增量较大,分组较多,每组的元素个数少,故各组内直接插入较快,后来增量di逐渐缩小,分组数逐渐减少,而各组的元素个数逐渐增多,但由于已经按di-1(比如我们示意图中的第一趟增量increment = 2)作为距离排过序,使元素列较接近于有序状态,所以新的一趟排序过程也较快。
因此,希尔排序在效率上较直接插入排序有较大的改进。
算法稳定性
希尔排序可能会调换两个相同元素的先后位置,所以希尔排序是一种不稳定的排序算法。例如{1,8,5,5},就会调换两个相同元素5的先后位置。
空间复杂度
希尔排序辅助移动的变量空间只有一个临时变量(即代码中的T temp),并且不会随着数据规划的扩大而变大,所以希尔排序的空间复杂度为:O(1)
五、快速排序
快速排序(Quick Sort),是对冒泡排序的一种改进,它的工作原理为:
(1) 在待排序的元素列中选一个元素为分界值,为了方便算法的实现,一般选待排序的元素列中的第一个元素作为分界值。
(2) 然后从待排序的元素列的最右边未查找过的元素中开始找,直到找到比这个分界值小的元素,进行交换。
(3) 然后再从最左边未查找过的元素中开始找,直到找到比这个分界值大于或等于的元素,进行交换。
(4) 然后循环(2)(3),直到查找交换完,这时大于或等于这个分界值的元素,都分布在这个分界值的右边,小于这个分界值的元素,都分布在这个分界值的左边。
(5) 重复上述过程,可以看出,这是一个递归定义。通过递归将左侧部分排好序后,再递归排好右侧部分的顺序。当左、右两个部分各元素排序完成后,整个元素列的排序也就完成了。
排序思路示意图:
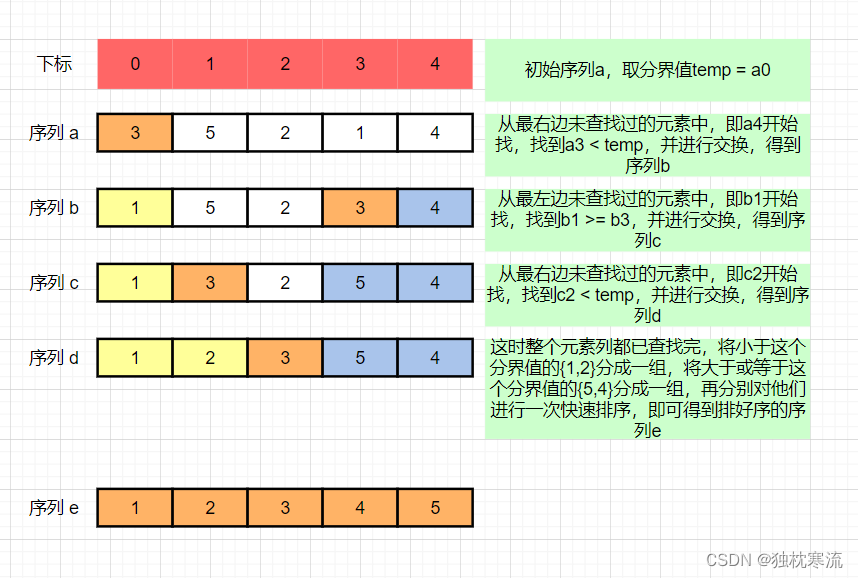
实现代码:
//C++版本
#include <iostream>
using namespace std;
template<typename T>
void quick_sort(T *pArr, int left, int right)
{
if (right <= left)
return;
int l = left;
int r = right;
T temp = pArr[left]; //待排序的元素列中的第一个元素为分界值
while(r > l) //从最右边开始找
{
if (pArr[r] < temp) //找到比这个分界值小的元素,进行交换
{
pArr[l] = pArr[r];
pArr[r] = temp;
l++;
while(l < r) //然后从左边开始找
{
if (pArr[l] >= temp) //找到比这个分界值大于或等于的元素,进行交换
{
pArr[r] = pArr[l];
pArr[l] = temp;
break;
}
l++;
}
}
if (l >= r) //防止上面while(l < r) 这个循环一直到 l = r,这时是不用执行r--;语句的
break;
r--;
}
quick_sort(pArr, left, r - 1);
quick_sort(pArr, r + 1, right);
}
int main()
{
//int arr[] = {3,2,1,1,3};
int arr[] = {3,5,2,1,4};
int len = sizeof(arr)/sizeof(*arr);
int i;
cout << "---before quick sort---" << endl;
for (i = 0; i < len; i++)
{
cout << arr[i] << " ";
}
cout << endl;
int left = 0;
int right = len - 1;
quick_sort(arr, left, right);
cout << "---after quick sort---" << endl;
for (i = 0; i < len; i++)
{
cout << arr[i] << " ";
}
cout << endl;
return 0;
}
运行结果:

时间复杂度
快速排序的一次划分算法从两头交替查找,直到left和right重合,因此其时间复杂度是O(n);而整个快速排序算法的时间复杂度与划分的趟数有关。
1.最优的情况是,每次划分所选择的分界值恰好将当前序列几乎等分,经过log2n趟划分,便可得到长度为1的子表。所以,整个快速排序算法的最优的时间复杂度为:O(nlog2n)
2.最坏的情况是,每次所选的分界值是当前序列中的最大或最小元素,这使得每次划分所得的子表中一个为空表,另一子表的长度为原表的长度-1。这样,长度为n的元素列的快速排序需要经过n趟划分,所以,整个排序算法的最坏的时间复杂度为:O(n2)
为了改善最坏情况下的时间性能,通常可采用“三者值取中”方法,即比较最左边的值、最中间的值,最右边的值,取三者中大小排在中间的元素为分界值。
算法稳定性
快速排序可能会调换两个相同元素的先后位置,所以快速排序是不稳定的排序算法。
空间复杂度
快速排序只需要一个元素的辅助空间,但快速排序需要一个栈空间来实现递归。
1.最优的情况,即快速排序的每一趟排序都将元素序列均匀地分割成长度相近的两个子表,所需栈的最大深度为log2(n+1)
2.最坏的情况下,栈的最大深度为n
综上所述。所以快速排序的空间复杂度为:O(log2n)