目录
1. 创建二叉树
1.1 二叉链表存储
typedef int BTDataType;
typedef struct BinaryTreeNode
{
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
BTDataType data;
}BTNode;
1.2 创建结点
BTNode* BuyNode(BTDataType x)
{
BTNode* node = (BTNode*)malloc(sizeof(BTNode));
assert(node);
node->data = x;
node->left = NULL;
node->right = NULL;
return node;
}
1.3 插入数据
BTNode* CreatBinaryTree()
{
BTNode* node1 = BuyNode(1);
BTNode* node2 = BuyNode(2);
BTNode* node3 = BuyNode(3);
BTNode* node4 = BuyNode(4);
BTNode* node5 = BuyNode(5);
BTNode* node6 = BuyNode(6);
BTNode* node7 = BuyNode(7);
node1->left = node2;
node1->right = node4;
node2->left = node3;
node4->left = node5;
node4->right = node6;
node3->right = node7;
return node1;
}
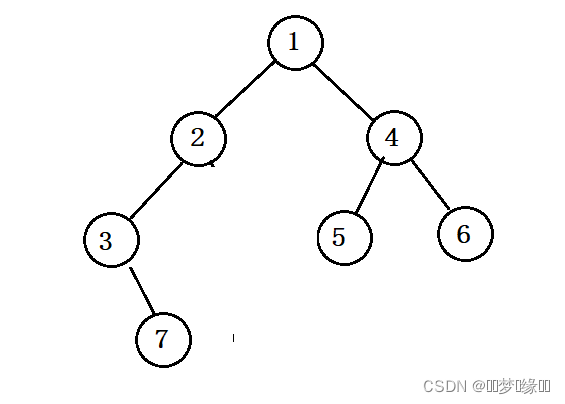
一颗完整的二叉树就创建好了,整体结构如下图:?
?
?
2.?二叉树的常规操作
2.1 二叉树的前中后序遍历
我们需要使用什么方式将存储好的二叉树遍历出来呢?我们常用的方法有三种,分别是:
前序遍历、中序遍历、后序遍历。
- 前序遍历:对树结构中的某个节点来说,先打印根,再打印他的左子书,最后打印它的右子树。
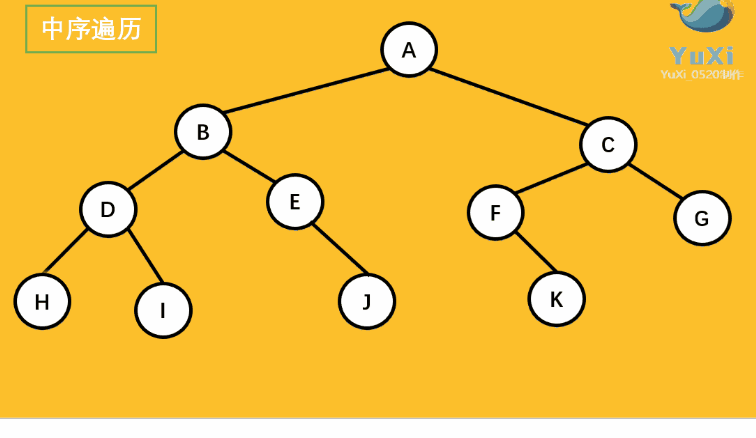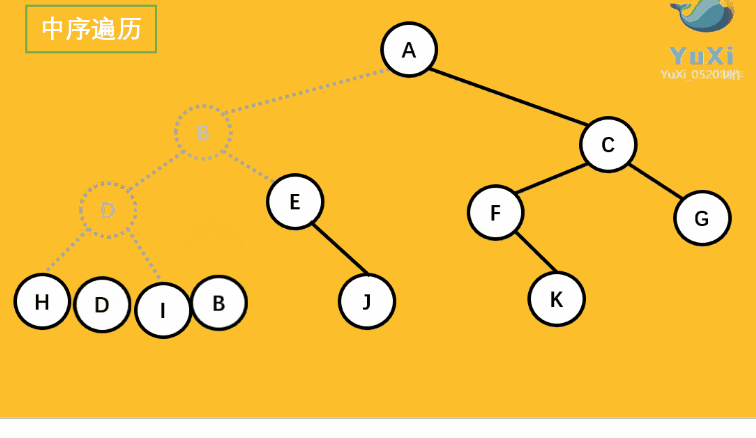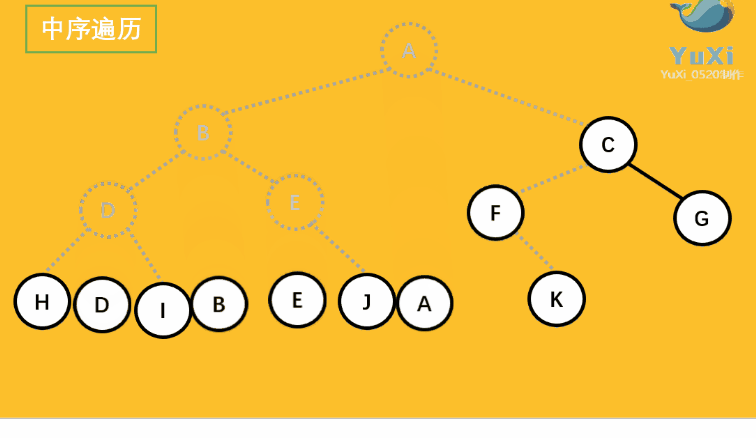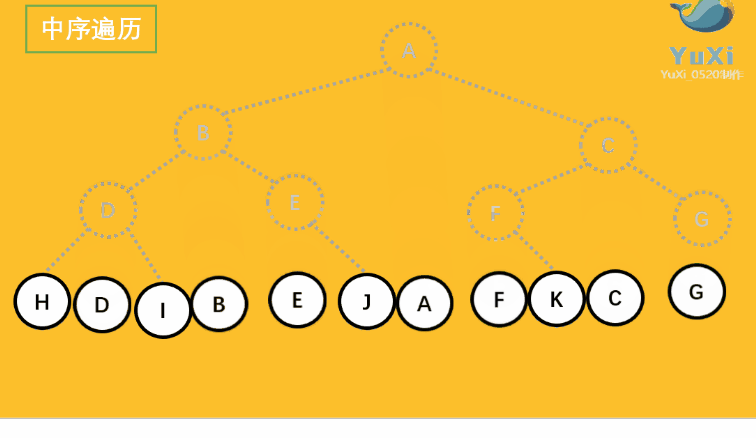
- 中序遍历:对树结构中的某个节点来说,先打印它的左子树,再打印根,最后打印它的右子树。
- 后序遍历:对树结构中的某个节点来说,先打印它的左子树,再打印它的右子树,最后打印根。
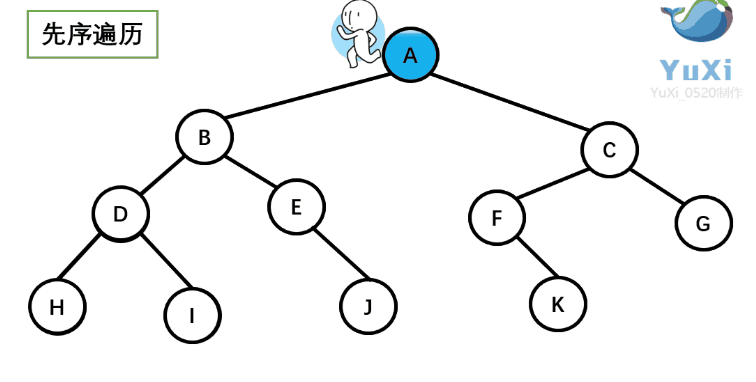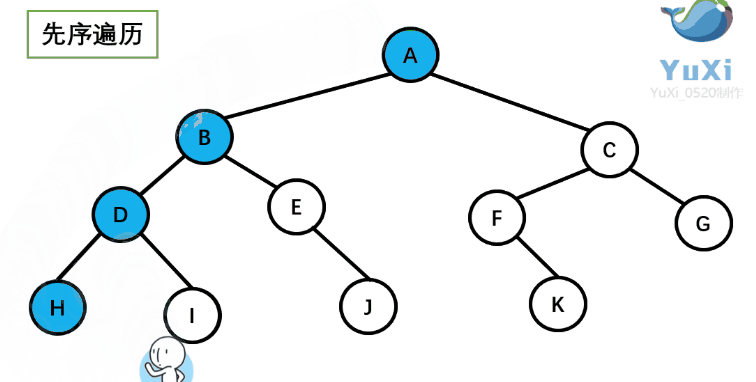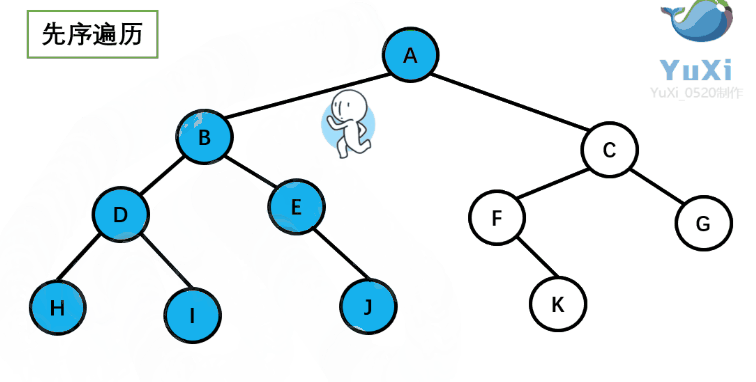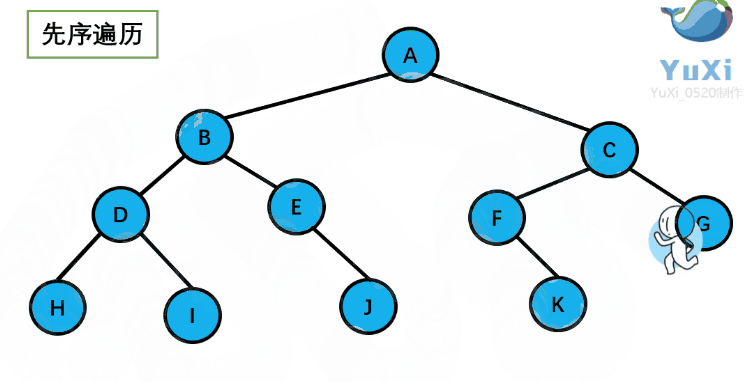
2.1.1 前序遍历?
?
?从树根开始绕着整棵树的外围转一圈,经过结点的顺序就是先序遍历的顺序
先序遍历结果:ABDHIEJCFKG
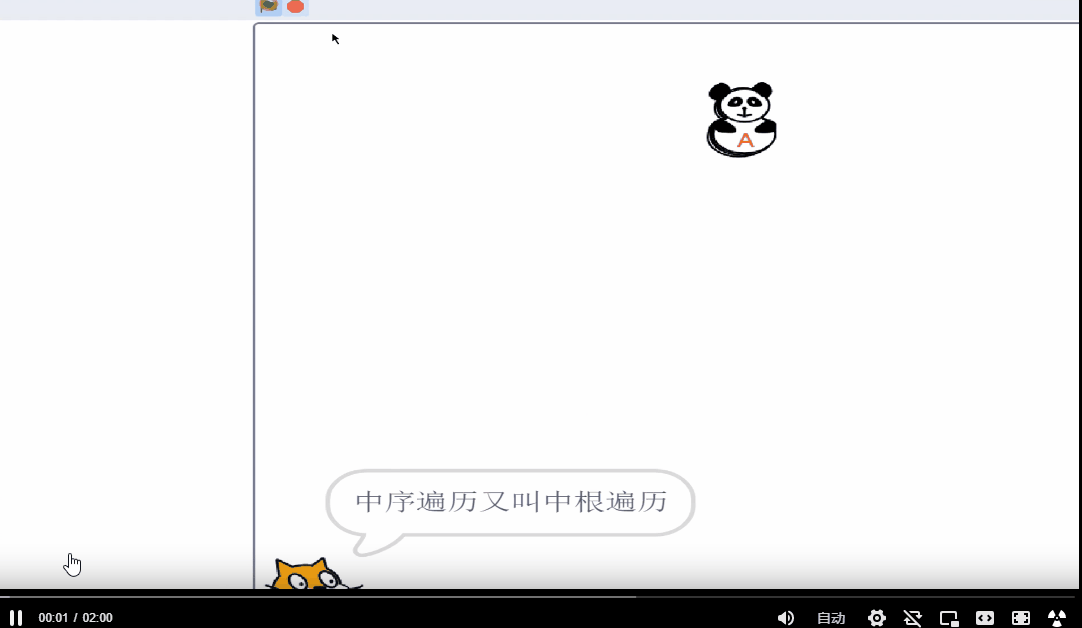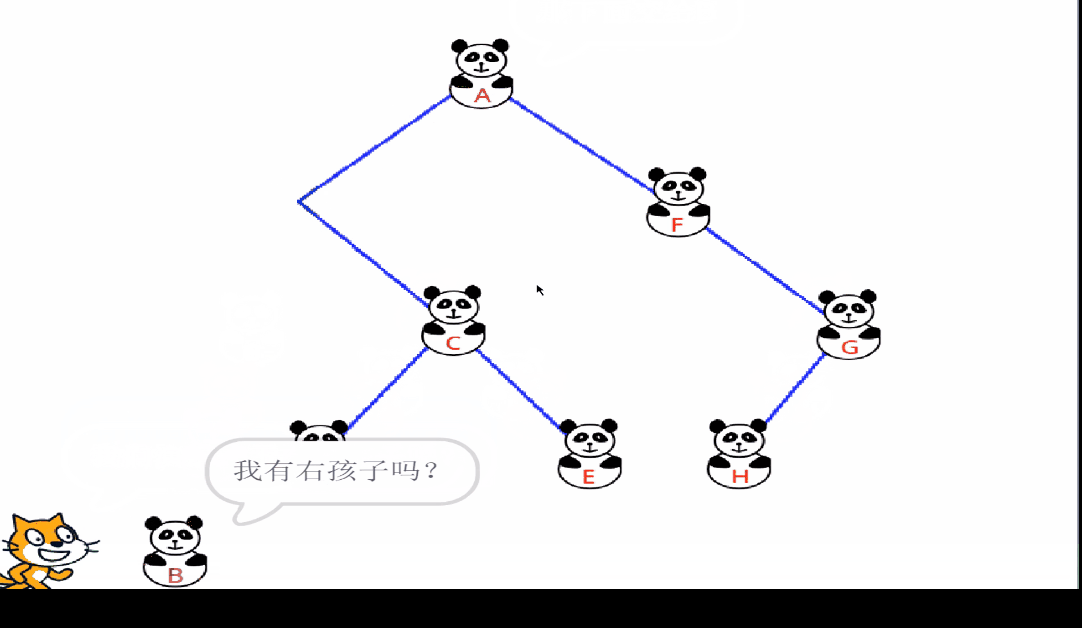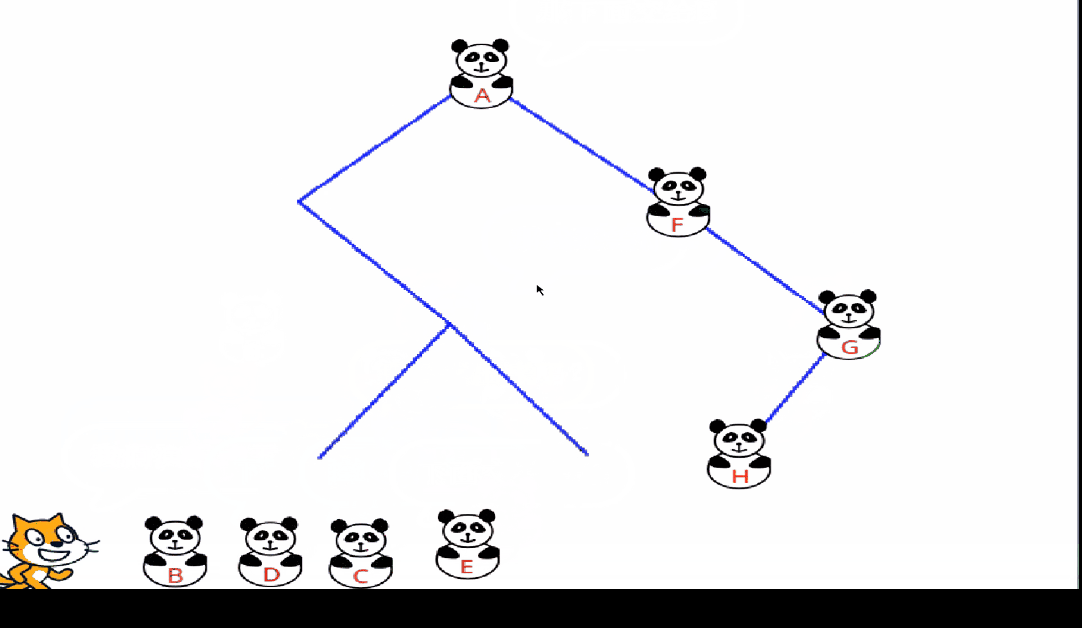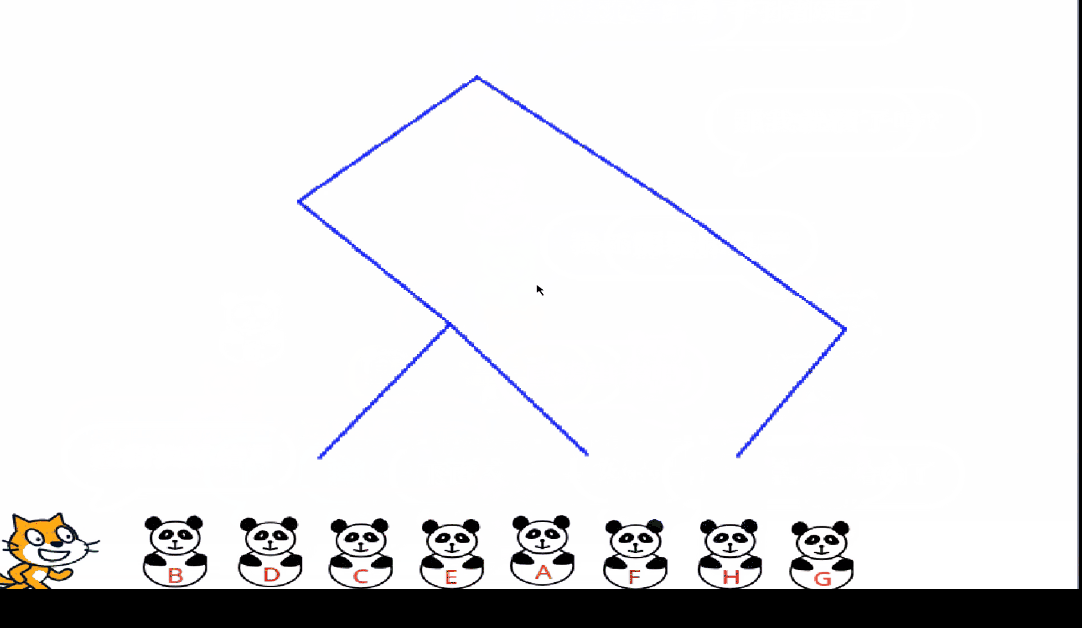
?2.1.2 中序遍历
?
?
?来源
中序遍历可以想象成,按树画好的左右位置投影下来就可以了
中序遍历结果:HDIBEJAFKCG
?
2.1.3 后序遍历
后序遍历就像是剪葡萄,我们要把一串葡萄剪成一颗一颗的。所以必须是从下面开始剪,如果发现一剪刀就能剪下的葡萄(必须是一颗葡萄),就把它剪下来,组成的就是后序遍历了。
后序遍历结果:HIDJEBKFGCA
2.1.4 代码实现
//先序遍历 void PreOrder(BTNode* root) { if (root == NULL) { printf("# "); return; } printf("%d ", root->data); PreOrder(root->left); PreOrder(root->right); } //中序遍历 void InOrder(BTNode* root) { if (root == NULL) { printf("# "); return; } InOrder(root->left); printf("%d ", root->data); InOrder(root->right); } //后序遍历 void PostOrder(BTNode* root) { if (root == NULL) { printf("# "); return; } PostOrder(root->left); PostOrder(root->right); printf("%d ", root->data); }我们是用递归的方式写的,用先序遍历画递归展开图刨析一下?
?
?2.2?二叉树的层序遍历
为什么要把层序遍历二叉树的层序遍历单独拿出来,因为它的实现需要用到 队列
?
?父节点出队列的同时把它的孩子入队列,直到队列为空,结束遍历。
void LevelOrder(BTNode* root) { Queue q; QueueInit(&q); if (root) { QueuePush(&q, root); } while (!QueueEmpty(&q)) { BTNode* front = QueueFront(&q); printf("%d ", front->data); QueuePop(&q); if (front->left) { QueuePush(&q, front->left); } if (front->right) { QueuePush(&q, front->right); } } printf("\n"); QueueDestory(&q); }
2.3?二叉树结点的个数
二叉树的节点个数可以看成是 根 + 左子树的节点个数 + 右子树的节点个数,如果为NULL,就返回0。这就可以用分治的思想来写。
int TreeSize(BTNode* root) { return root == NULL ? 0 : TreeSize2(root->left) + TreeSize2(root->right) + 1; }
2.4?二叉树叶子节点的个数
什么样的节点才是叶子节点呢? 左右子树都为空树。
我们只要在上面的基础加入判断即可。
int TreeLeafSize(BTNode* root) { if (root == NULL) return 0; if (root->left == NULL && root->right == NULL) return 1; return TreeLeafSize(root->left) + TreeLeafSize(root->right); }
2.5?二叉树第k层节点个数
可以看成是求第k-1层节点的孩子结点个数?。
int TreeKLevel(BTNode* root, int k) { assert(k >= 1); if (root == NULL) return 0; if (k == 1) return 1; return TreeKLevel(root->left, k - 1) + TreeKLevel(root->right, k - 1); }
2.6?查找值为x的节点
用前序遍历进行查找
为什么不用其他遍历方法呢? 因为用前序遍历,只要找到就能返回节点,其他的方法找到了还要查找 左子树和右子树。
BTNode* TreeFind(BTNode* root, BTDataType x) { if (root == NULL) return NULL; if (root->data == x) return root; BTNode* ret1 = TreeFind(root->left, x); if (ret1) return ret1; BTNode* ret2 = TreeFind(root->right, x); if (ret2) return ret2; return NULL; }
2.7 求二叉树的深度
我们用 leftDepth 记录左子树的高度,用 rightDepth 记录右子树的高度,然后更新,进行对比
int TreeDepth(BTNode* root) { if (root == NULL) return 0; int leftDepth = TreeDepth(root->left); int rightDepth = TreeDepth(root->right); return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1; }
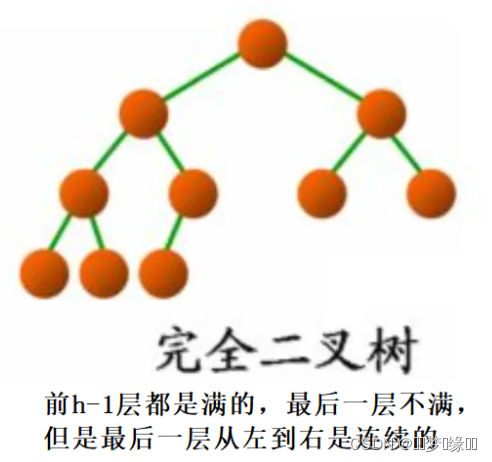
2.8?判断二叉树是否为完全二叉树?
完全二叉树
?
我们按照层序遍历的方法把所有的节点(包括NULL)全部入队列,只需要遍历队列直到有NULL的节点,如果在这之后都是NULL,那么就是完全二叉树;如果在这之后有不是NULL的节点,那么就不是完全二叉树。
?
?
?
bool TreeComplete(BTNode* root) { Queue q; QueueInit(&q); if (root) { QueuePush(&q, root); } while (!QueueEmpty(&q)) { BTNode* front = QueueFront(&q); QueuePop(&q); if (front) { QueuePush(&q, front->left); QueuePush(&q, front->right); } else { break; } } //后面全是空,则是完全二叉树 while(!QueueEmpty(&q)) { BTNode* front = QueueFront(&q); QueuePop(&q); if (front) { QueueDestory(&q); return false; } } QueueDestory(&q); return true; }
2.9 二叉树的销毁
先销毁孩子节点,再销毁根节点。(后序遍历)
void TreeDestory(BTNode* root) { if (root == NULL) return; TreeDestory(root->left); TreeDestory(root->right); free(root); }