😀如果对你有帮助的话😊
🌺为博主点个赞吧 👍
👍点赞是对博主最大的鼓励😋
💓爱心发射~💓
【动态规划整理合集】
【力扣——动态规划】整理题目1:基础题目:509、70、746、62、63、343、96
【力扣—动态规划】整理题目2:背包问题:0-1背包、完全背包
目录
动态规划总结
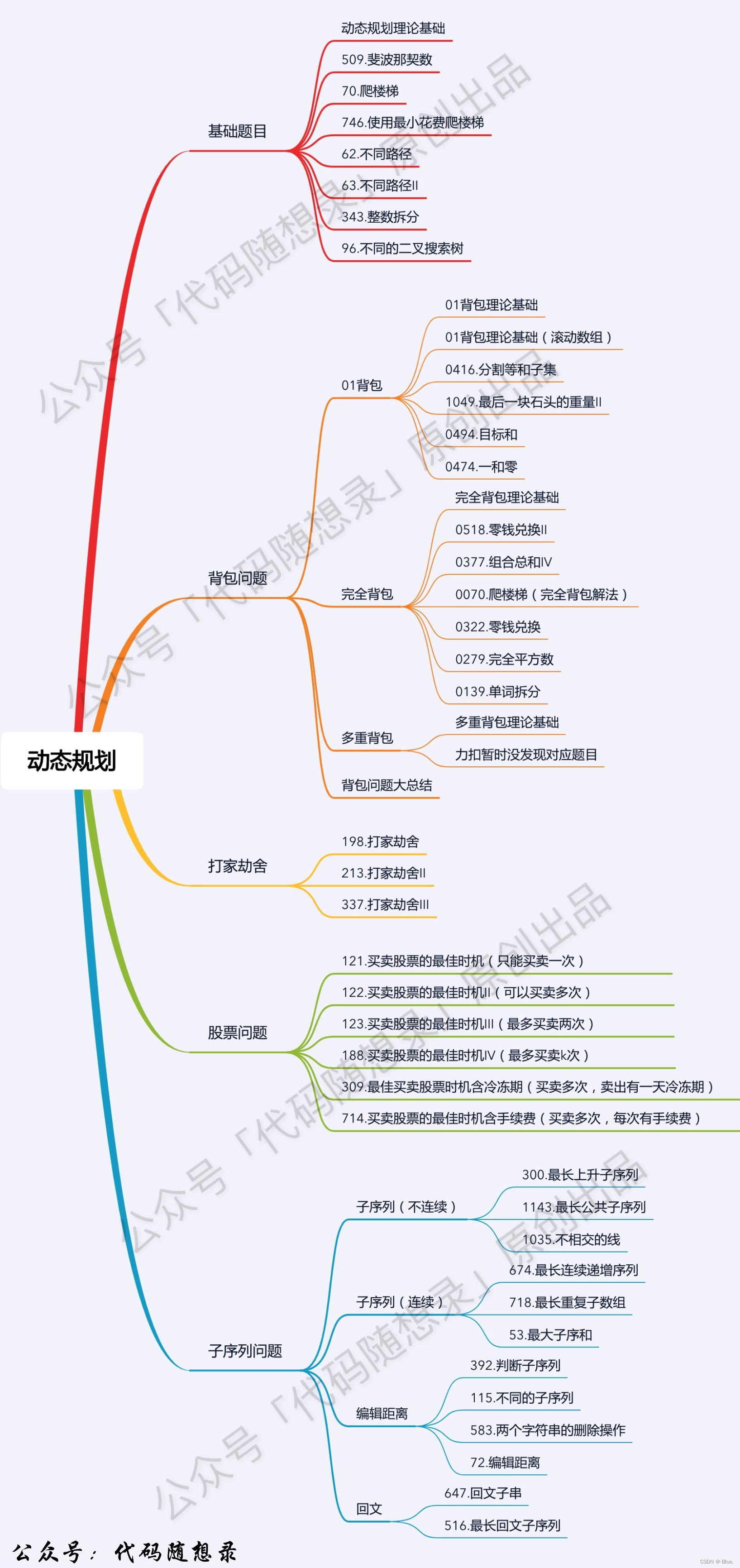
0-1背包
- 面试的话,其实掌握
01背包,和完全背包,就够用了,最多可以再来一个多重背包。 - 背包问题的理论基础重中之重是
01背包
基础知识
- 动态规划是由前一个状态推导出来的
- 而贪心算法是局部直接选最优的
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
解题步骤
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
解题步骤-简洁
- 确定dp数组下标含义
- 递推公式
- 初始化
- 遍历顺序
- 推导结果
例1
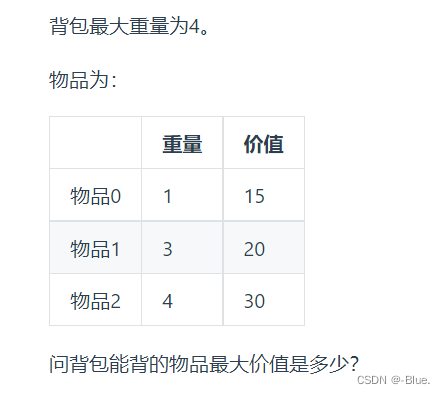
1、确定dp数组下标含义
dp[i][j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少
2、递推公式
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
3、初始化
// 初始化 dp
//初始化:背包容量为0时,能获得的价值都为0
for (int i = 0; i <= wlen; i++){
dp[i][0] = value0;
}
4、遍历顺序
先物品后背包、或者先背包后物品,都可以
5、推导结果
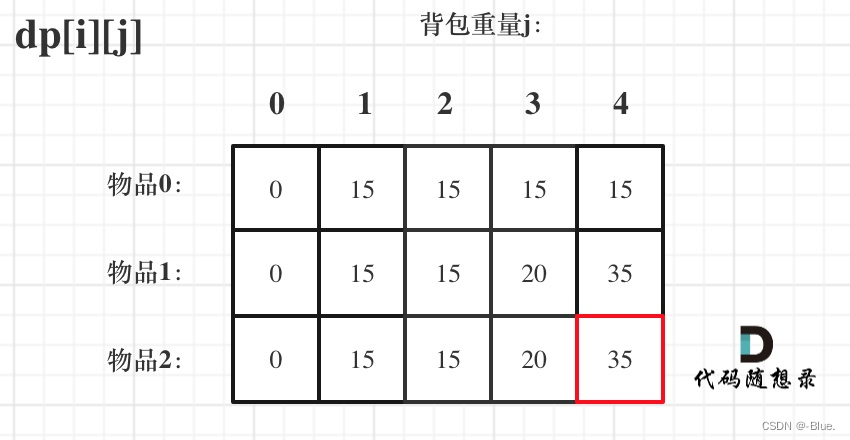
public static void main(String[] args) {
int[] weight = {1, 3, 4};
int[] value = {15, 20, 30};
int bagsize = 4;
testweightbagproblem(weight, value, bagsize);
}
public static void testweightbagproblem(int[] weight, int[] value, int bagsize){
int wlen = weight.length, value0 = 0;
//定义dp数组:dp[i][j]表示背包容量为j时,前i个物品能获得的最大价值
int[][] dp = new int[wlen + 1][bagsize + 1];
//初始化:背包容量为0时,能获得的价值都为0
for (int i = 0; i <= wlen; i++){
dp[i][0] = value0;
}
//遍历顺序:先遍历物品,再遍历背包容量
for (int i = 1; i <= wlen; i++){
for (int j = 1; j <= bagsize; j++){
if (j < weight[i - 1]){
dp[i][j] = dp[i - 1][j];
}else{
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i - 1]] + value[i - 1]);
}
}
}
//打印dp数组
for (int i = 0; i <= wlen; i++){
for (int j = 0; j <= bagsize; j++){
System.out.print(dp[i][j] + " ");
}
System.out.print("\n");
}
}
例2
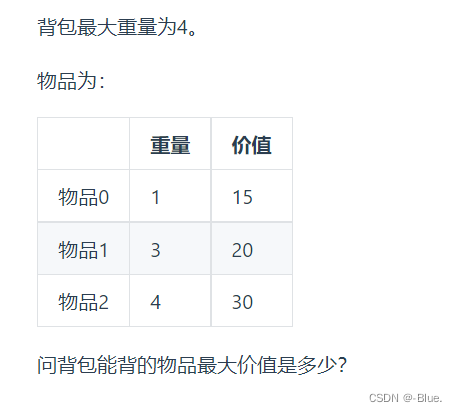
1、确定dp数组下标含义
在一维dp数组中,dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j]
2、递推公式
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
3、初始化
int[] dp = new int[bagWeight + 1];
4、遍历顺序
先物品后背包
5、推导结果
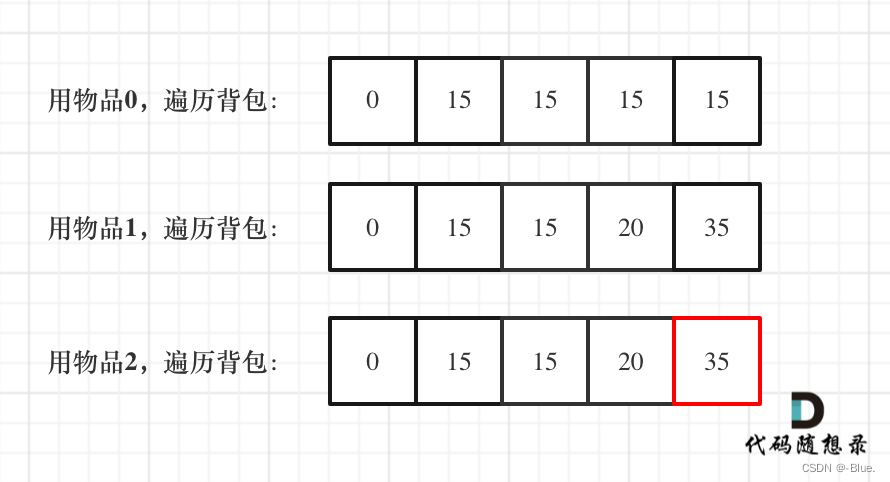
public static void main(String[] args) {
int[] weight = {1, 3, 4};
int[] value = {15, 20, 30};
int bagWight = 4;
testWeightBagProblem(weight, value, bagWight);
}
public static void testWeightBagProblem(int[] weight, int[] value, int bagWeight){
int wLen = weight.length;
//定义dp数组:dp[j]表示背包容量为j时,能获得的最大价值
int[] dp = new int[bagWeight + 1];
//遍历顺序:先遍历物品,再遍历背包容量
for (int i = 0; i < wLen; i++){
for (int j = bagWeight; j >= weight[i]; j--){
dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
}
}
//打印dp数组
for (int j = 0; j <= bagWeight; j++){
System.out.print(dp[j] + " ");
}
}
416. 分割等和子集

题解
class Solution {
public boolean canPartition(int[] nums) {
// 0-1背包
/*
1. 确定dp数组下标含义: dp[j] 表示: 容量为j的背包,所背的物品价值可以最大为dp[j]
2. 递推公式 : dp[j] = max( dp[j], dp[j-num[i]+num[i]])
3. 初始化 : 都为 0
4. 遍历顺序
5. 推导结果
*/
if(nums == null || nums.length ==0) return false;
int n = nums.length;
int sum = 0;
for(int num : nums){
sum += num;
}
if(sum % 2 != 0 ) {
return false;
}
int target = sum/2;
int[] dp = new int[target+1];
for(int i=0; i<n; i++){
for(int j=target; j>=nums[i]; j--){
dp[j] = Math.max(dp[j], dp[j-nums[i]]+nums[i]);
}
}
return dp[target] == target;
}
}
1049. 最后一块石头的重量 II


题解
class Solution {
public int lastStoneWeightII(int[] stones) {
/*
0-1背包:
1. 确定dp数组下标含义: dp[j] 表示: 容量为j的背包,所背的石头最大重量为dp[j]
2. 递推公式 : dp[j] = max( dp[j], dp[j-stones[i]+]stones[i])
3. 初始化 : 最大重量就是30 * 1000 ,target 为 15000
4. 遍历顺序 外层物品,内层背包
5. 推导结果 (sum - dp[target]) - dp[target]
*/
int sum = 0;
for(int num : stones){
sum += num;
}
int target = sum / 2;
int dp[] = new int[target + 1];
for(int i=0; i<stones.length; i++){
for(int j=target; j>=stones[i]; j--){
dp[j] = Math.max(dp[j], dp[j-stones[i]]+stones[i]);
}
}
return (sum-dp[target]) - dp[target];
}
}
494. 目标和——组合背包


题解
class Solution {
public int findTargetSumWays(int[] nums, int target) {
/*
left - right = target
left + right = sum
left = (target + sum)/2
装满 容量为 left 的背包 有几种方法
1. 确定dp数组下标的含义 dp[j] 表示:填满j(包括j)这么大容积的包,有dp[j]种方法
2. 确定递推公式 dp[j] += dp[j - nums[i]]
3. dp数组如何初始化 dp[0]=1
4. 确定遍历顺序 nums 在外边, target在内部
5. 举例推导dp数组
*/
int sum = 0;
for(int i=0; i<nums.length; i++){
sum += nums[i];
}
if(Math.abs(target)>sum) return 0;
if((target + sum) % 2 !=0 ) return 0;
int size = (target + sum) /2;
if(size<0) size = -size;
int[] dp = new int[size+1];
dp[0] = 1;
for(int i=0; i<nums.length; i++){
for(int j=size; j>=nums[i]; j--){
dp[j] += dp[j - nums[i]];
}
}
return dp[size];
}
}
474. 一和零


题解
class Solution {
public int findMaxForm(String[] strs, int m, int n) {
/*
1. 确定dp数组下标含义 dp[i][j]:最多有i个0和j个1的strs的最大子集的大小为dp[i][j]
2. 递推公式 dp[i][j] = max(dp[i][j], dp[i-zero][j-one]+1)
3. 初始化 0
4. 遍历顺序 从后向前遍历
5. 推导结果
*/
int[][] dp = new int[m+1][n+1];
int zero, one;
for(String str : strs){
zero=0;
one=0;
for(char ch : str.toCharArray()){
if(ch == '0'){
zero++;
}else{
one++;
}
}
for(int i=m; i>=zero; i--){
for(int j=n; j>=one; j--){
dp[i][j] = Math.max(dp[i][j], dp[i-zero][j-one]+1);
}
}
}
return dp[m][n];
}
}
完全背包
518. 零钱兑换 II ——排列


- 排列数:先背包,后物品
题解
class Solution {
public int change(int amount, int[] coins) {
/*
1. 确定dp数组下标含义 dp[j]:凑成总金额j的货币组合数为dp[j]
2. 递推公式 dp[j] += dp[j - coins[i]];
3. 初始化 dp[0]=1
4. 遍历顺序 先物品,在背包
5. 推导结果
*/
int[] dp = new int[amount+1];
dp[0] = 1;
for(int i=0; i<coins.length; i++){
for(int j=coins[i]; j<=amount; j++){
dp[j] += dp[j - coins[i]];
}
}
return dp[amount];
}
}
377. 组合总和 Ⅳ——排列
- 排列数:先背包,后物品
题解
class Solution {
public int combinationSum4(int[] nums, int target) {
/*
完全背包
1. 确定dp数组下标含义 dp[j]: 凑成目标正整数为j的排列个数为dp[j]
2. 递推公式 dp[j] += dp[j-nums[i]]
3. 初始化 dp[0] = 1
4. 遍历顺序 外部target 内部nums 从前到后
5. 推导结果
*/
int[] dp = new int[target + 1];
dp[0]=1;
for(int j=0; j<=target; j++){
for(int i=0; i<nums.length; i++){
if(j>=nums[i]){
dp[j] += dp[j-nums[i]];
}
}
}
return dp[target];
}
}
70. 爬楼梯 ——排列


- 排列数:先背包,后物品
题解
class Solution {
public int climbStairs(int n) {
/*
完全背包
1. 确定dp数组下标含义 dp[j]:爬到台阶j有dp[j]方法
2. 递推公式 dp[j] += dp[j-i]
3. 初始化 dp[0]=1
4. 遍历顺序 target 在外 nums在里 从前向后
5. 推导结果
*/
int[] dp = new int[n+1];
int[] nums = {1,2};
dp[0]=1;
for(int j=0; j<=n; j++){
for(int i=0; i<nums.length; i++){
if(j >= nums[i]){
dp[j] += dp[j-nums[i]];
}
}
}
return dp[n];
}
}
322. 零钱兑换


题解
class Solution {
public int coinChange(int[] coins, int amount) {
/*
完全背包
1. 确定dp数组下标含义 dp[j]:凑足总额为j所需钱币的最少个数为dp[j]
2. 递推公式 dp[j] = min(dp[j-coins[i]]+1, dp[j])
3. 初始化 dp[0]=0 其他 都为最大值
4. 遍历顺序 coins 在外 amount 在里 从前向后
5. 推导结果
*/
int max = Integer.MAX_VALUE;
int[] dp = new int[amount+1];
//初始化dp数组为最大值
for (int j = 0; j < dp.length; j++) {
dp[j] = max;
}
dp[0] = 0;
for(int i=0; i<coins.length; i++){
for(int j=coins[i]; j<= amount; j++){
//只有dp[j-coins[i]]不是初始最大值时,该位才有选择的必要
if(dp[j - coins[i]] != max){
dp[j] = Math.min(dp[j-coins[i]]+1, dp[j]);
}
}
}
return dp[amount] == max? -1:dp[amount];
}
}
279. 完全平方数

题解
class Solution {
public int numSquares(int n) {
/*
完全背包
1. 确定dp数组下标含义 dp[j]:和为j的完全平方数的最少数量为dp[j]
2. 递推公式 dp[j] = min(dp[j-i*i]+1, dp[j])
3. 初始化 dp[0]=0 其他 都为最大值
4. 遍历顺序 coins 在外 amount 在里 从前向后
5. 推导结果
*/
int max = Integer.MAX_VALUE;
int[] dp = new int[n+1];
for(int j=0; j<dp.length; j++){
dp[j] = max;
}
dp[0] = 0;
for(int i=1; i*i<=n; i++){
for(int j = i*i; j<=n; j++){
if(dp[j - i*i] != max){
dp[j] = Math.min(dp[j], dp[j-i*i]+1);
}
}
}
return dp[n];
}
}
139. 单词拆分
题解
class Solution {
public boolean wordBreak(String s, List<String> wordDict) {
/*
完全背包
1. 确定dp数组下标含义 dp[i] : 字符串长度为i的话,dp[i]为true,
2. 递推公式 dp[j] =
3. 初始化 dp[0]=true 其他 都为最大值
4. 遍历顺序 s 在外 amount 在里 从前向后
5. 推导结果
*/
boolean[] dp = new boolean[s.length() + 1];
dp[0] = true;
for(int i=1; i<=s.length(); i++){
for(int j=0; j<i; j++){
if(wordDict.contains(s.substring(j,i)) && dp[j]){
dp[i] = true;
}
}
}
return dp[s.length()];
}
}
总结