198—打家劫舍(一)
题目描述
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
解题思路
- 因为相邻房间不能连续偷盗,所以采用间隔偷盗;
- 需要选择偷盗金额高的进行偷盗,最终可以偷盗到比较大的金额;
- 在第 k 个房屋面前,面临两种情况:
- 如果偷第 k 间房屋,那么 k-1 间房屋就不能进行偷窃,这时的最大金额应该是 k-2 的最大金额加上当前第 k 间房屋的财富;
- 如果不偷第 k 间房屋,那么这时的最大金额应该是 k-1 的最大金额。
- 所以在每个房屋面前,我们有两种选择,我们所获得的最大金额应该在这两种情况中取较大值;
- 所以状态转移方程就可以写为:
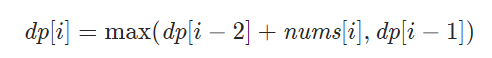
?放一组力扣官方的示意图,方便我们理解题意:
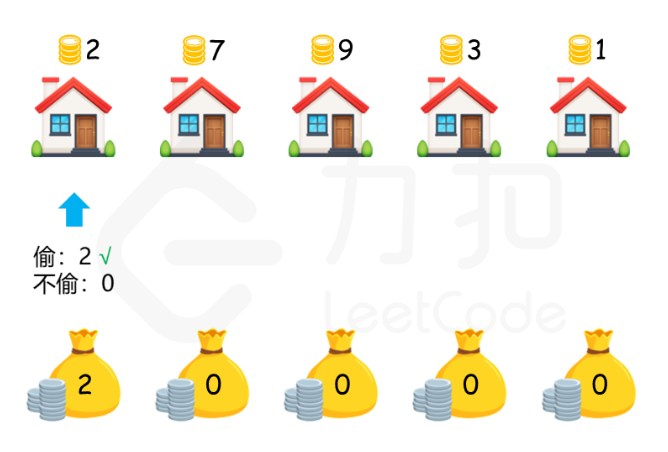
?
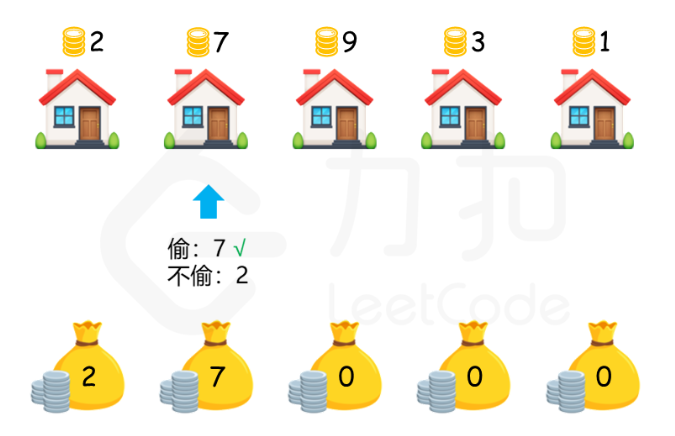
?
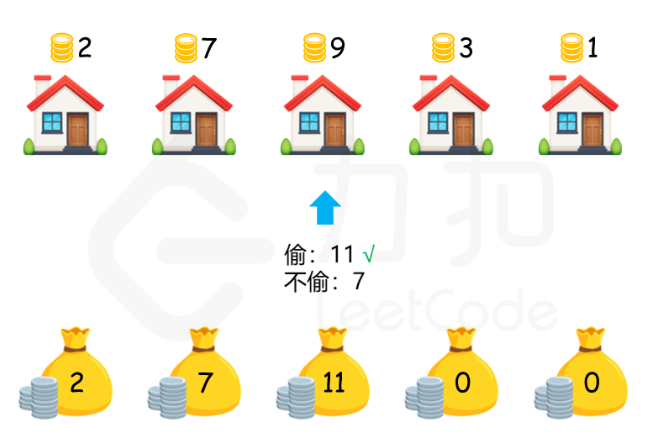
?

?

?
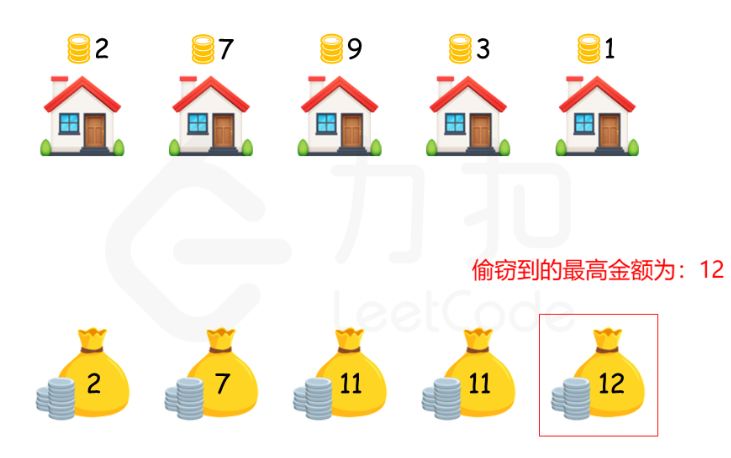
?
输入输出示例

代码
需要创建两个指针来表示当前房屋的前面两个房屋的最大金额,然后动态更新两个指针变量,也可以理解为动态区间法。
class Solution {
public int rob(int[] nums) {
int len = nums.length;
int sum = 0;
int p = 0;//记录房屋 nums[i- 2] 状态的偷窃到的最大金额;
int q = 0;//记录房屋 nums[i- 1] 状态的偷窃到的最大金额;
for(int i = 0; i < len; i++ ){
sum = Math.max(p+nums[i], q);//记录房屋当前 nums[i] 状态的偷窃到的最大金额;
p = q;
q = sum;
}
return q;
}
}213—打家劫舍(二)
题目描述
你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警 。
给定一个代表每个房屋存放金额的非负整数数组,计算你 在不触动警报装置的情况下 ,今晚能够偷窃到的最高金额。
解题思路
- 这两道题目其实思路是差不多的,只是这道题目假设所有的房屋是连在一起闭环的;
- 那么我们就可以理解为:偷首就不能偷尾,偷尾就不能偷首;
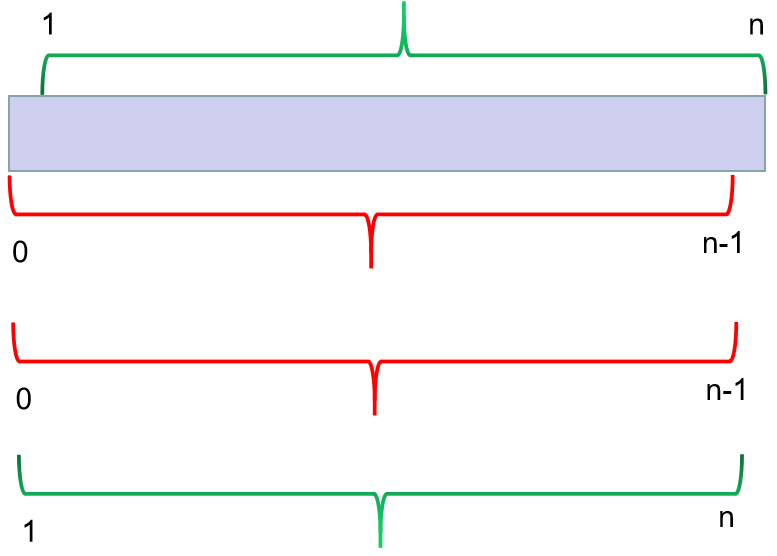
- 所以我们就可以把原来的环状数组拆分为两个数组,一条是 0 ——n - 1,另一条是 1—— n ;
- 然后在两种方案里面选择结果较大的就是此题的解。
输入输出示例

代码
代码或许可以再精简一下~
class Solution {
public int rob(int[] nums) {
if(nums.length == 1)return nums[0];
int p1 = 0;
int q1 = 0;
for(int i = 0; i < nums.length-1; i++){
int sum1 = Math.max(p1 + nums[i],q1);
p1 = q1;
q1 = sum1;
}
int p2 = 0;
int q2 = 0;
for(int i = 1; i < nums.length; i++){
int sum2 = Math.max(p2 + nums[i],q2);
p2 = q2;
q2 = sum2;
}
return Math.max(q1,q2);
}
}