[数据结构与算法]【数据结构基础_数组】 Leetcode 240.搜索二维矩阵II （好题）

原题l链接：Leetcode 240. Search a 2D Matrix II

Write an efficient algorithm that searches for a value target in an m x n integer matrix matrix. This matrix has the following properties:

• Integers in each row are sorted in ascending from left to right.
• Integers in each column are sorted in ascending from top to bottom.

Example 1:

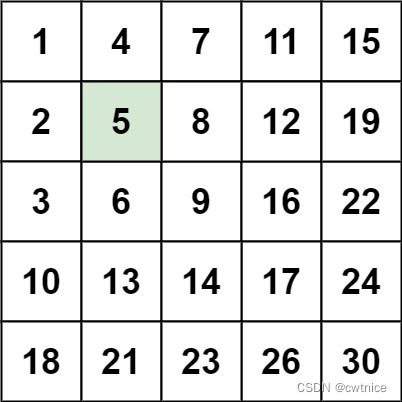
Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
Output: true

Example 2:

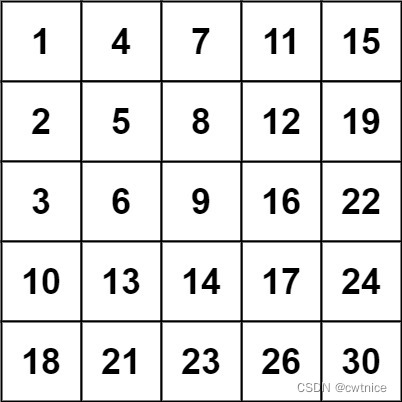
Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
Output: false

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= n, m <= 300
• -10⁹ <= matrix[i][j] <= 10⁹
• All the integers in each row are sorted in ascending order.
• All the integers in each column are sorted in ascending order.
• -10⁹ <= target <= 10⁹

方法一：Z型搜索

思路：

核心的想法就是 不断缩小搜索范围
因为从上到下和从左到右都是排序好的
可以从右上角或者左下角（因为这两个位置具有 单调性 ）开始搜索
以从右上角开始搜索为例：

• 当前值比目标元素大时，说明没必要往下走了（往下走更大），那就向左走
• 当前值比目标元素小时，同理，往下走

这是一个能不断缩小搜索范围的过程，最终能得到结果

大佬的思路理解：

[1,   4,  7, 11, 15],
[2,   5,  8, 12, 19],
[3,   6,  9, 16, 22],
[10, 13, 14, 17, 24],
[18, 21, 23, 26, 30]

如果 target  = 9，如果我们从 15 开始遍历, cur = 15
    
target < 15, 去掉当前列, cur = 11
[1,   4,  7, 11],
[2,   5,  8, 12],
[3,   6,  9, 16],
[10, 13, 14, 17],
[18, 21, 23, 26]    
    
target < 11, 去掉当前列, cur = 7  
[1,   4,  7],
[2,   5,  8],
[3,   6,  9],
[10, 13, 14],
[18, 21, 23]     

target > 7, 去掉当前行, cur = 8   
[2,   5,  8],
[3,   6,  9],
[10, 13, 14],
[18, 21, 23]       

target > 8, 去掉当前行, cur = 9, 遍历结束    
[3,   6,  9],
[10, 13, 14],
[18, 21, 23]   

作者：windliang
链接：https://leetcode.cn/problems/search-a-2d-matrix-ii/solution/xiang-xi-tong-su-de-si-lu-fen-xi-duo-jie-fa-by-5-4/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

c++代码：

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        // m行 n列
        // 必须是一加一减, 能保证逐渐逼近答案
        int m = matrix.size(), n = matrix[0].size();
        int x = 0, y = n - 1; 

        // 找到或者出界就停止循环
        while(x < m && y >= 0){
            if(matrix[x][y] == target)
                return true;
            
            // 当前值比目标值大, 说明目标值可能在左边, 向左移动
            if(matrix[x][y] > target)
                y--;
            // 否则就向下移动
            else
                x++;
        }

        return false;
    }
};

复杂度分析：

• 时间复杂度：O(m+n)，做多能向左走n步，向下走m行
• 空间复杂度：O(1)