[数据结构与算法]七大基本排序算法(升序排列)

?

目录

1.冒泡排序（Bubble Sort）

2.选择排序(SelectSort)

3.插入排序(InsertionSort)

4.希尔排序(ShellSort)

5.快速排序(QuickSort)

6.归并排序(MergeSort)

7.基数排序(RadixSort)

1.冒泡排序（Bubble Sort）

原理：每一趟只能确定将一个数归位。即第一趟将最大的数归位，第二趟将倒数第 2 大的数归位，依次类推下去。如果有 n 个数进行排序，只需将 n-1 个数归位，也就是要进行 n-1 趟操作。

而 “每一趟 ” 都需要从第一位开始进行相邻的两个数的比较，将较大的数放后面，比较完毕之后向后挪一位继续比较下面两个相邻的两个数大小关系，重复此步骤，直到最后一个还没归位的数。
?

public static void sort(int[] arr){
        int temp = 0;
//当一趟排序 位置没有发生改变证明数组是有序的 即可用一个标识符判断 减少不必要要的比较
        boolean flag = false; 
        for (int i = 0 ; i < arr.length;i++){
            for (int j = 0; j < arr.length-i-1; j++) {
                if (arr[j] > arr[j+1]){
                    flag = true;
                    temp = arr[j];
                    arr[j] = arr[j+1];
                    arr[j+1] = temp;
                }
            }
            if (!flag) break;
            if (flag) flag=false;
//            System.out.println("第"+(i+1)+"轮后:"+Arrays.toString(arr));
        }
    }

这次使用了一个表示符flag，防止数组已经有序，仍然在做无必要的排序遍历。当我们遍历一轮发现前面的数没有比后大的数，即没有经过if(arr[j] > arr[j+1])语句内，也就是数组有序，我们就会退出循环。

时间复杂度：O(n^2)

空间复杂度：O(1)

2.选择排序(SelectSort)

选择排序就是每次遍历比较出一个最小值min，并记下数组下标，再把它交换到数组前面，与冒泡排序有相似之处，但是选择排序每次遍历只会交换一次，而闹冒泡排序交换次数不确定。

原理很简单我们看看代码：

 public static void sort(int[] arr){
        int min = 0;
        int count = 0;
        for (int i = 0; i < arr.length; i++) {
            min = arr[i];
            int minIndex = i;
            for (int j = i+1; j < arr.length ; j++) {
                if (arr[j] < min){
                    min = arr[j];
                    minIndex = j;
                }
            }
            if (minIndex != i){   //当最小值数组下标变化了，就进行交换
                arr[minIndex] = arr[i];
                arr[i] = min;
            }
//            System.out.println("第"+(++count)+"轮后:"+Arrays.toString(arr));
        }
    }

时间复杂度：O(n^2)

空间复杂度：O(1)

3.插入排序(InsertionSort)

对于少量元素的排序，它是一个有效的算法。插入排序是一种最简单的排序方法，它的基本思想是将一个记录插入到已经排好序的有序表中，从而一个新的、记录数增 1 的有序表。在其实现过程使用双层循环，外层循环对除了第一个元素之外的所有元素，内层循环对当前元素前面有序表进行待插入位置查找，并进行移动?[2]??。

看原理我们可能不太好理解，我们可以看一个例子：

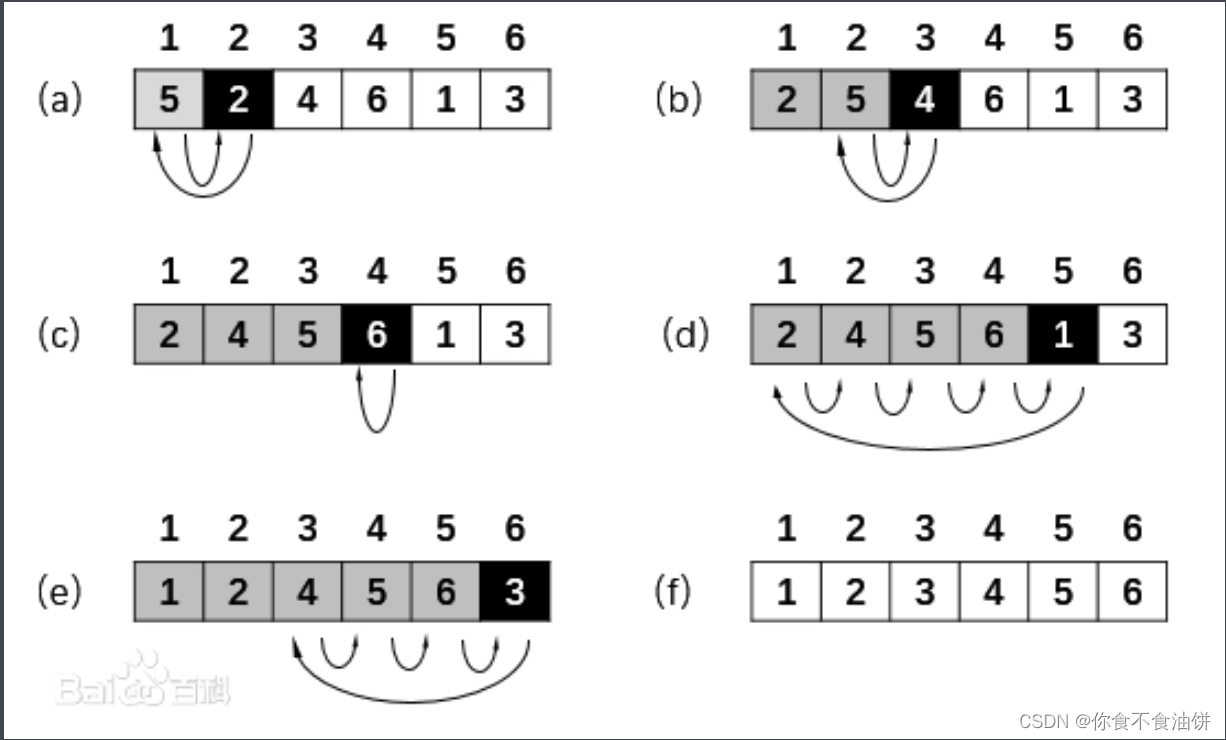
看图，我们可以理解为：

• 最开始把第一个数看为一个新数组，第二个数至最后一个数为一个数组
• 第一次遍历：从第二个数开始，2<5，所以2和5交换位置；(新数组：[2,5] 旧数组：[4,6,1,3])
• 第二次遍历：从第三个数开始，发现4<5，所以4和5交换位置；继续往前比较，发现4>2,所以此时不变；(新数组：[2,4,5] 旧数组：[6,1,3])
• 第三次遍历：从第四个数开始，发现6>5,所以位置不变；(新数组：[2,4,5,6] 旧数组：[1,3])
• 第四次遍历：从第四个数开始，发现1<6,所以1和6交换位置；(新数组：[2,4,5,1,6] 旧数组：[3])
• ? ? ? ? ? ? ? ? ? ? ? ?继续往前比较，发现1<5,所以1和5交换位置；(新数组：[2,4,1,5,6] 旧数组：[3])
• ? ? ? ? ? ? ? ? ? ? ? ?最后；(新数组：[1,2,4,5,6] 旧数组：[3])
• 第五次遍历：从第六个数开始一样的比较方法，最后；(新数组：[1,2,3,4,5,6] 旧数组：[])

相信经过一个例子的讲解，大家已经对插入排序有了一定认知，我们一起来看看代码吧！

    public static void sort(int[] arr) {
        int count = 0;  //用来打印排序的轮数
        int insertVal = 0; //用来表示要插入的那个值
        int insertIndex= 0;
        for (int i = 1; i < arr.length; i++) {
            insertVal = arr[i];  //要插入的值
            insertIndex = i - 1;
            while (insertIndex >= 0 && insertVal < arr[insertIndex]){
                arr[insertIndex + 1] = arr[insertIndex];
                insertIndex -- ;
            }
                arr[insertIndex + 1] = insertVal;
//            System.out.println("第"+(++count)+"轮的排序后的结果是"+ Arrays.toString(arr));
        }
    }

?时间复杂度：O(n^2)

空间复杂度: O(1)

4.希尔排序(ShellSort)

希尔排序又称缩小增量排序，是直接插入排序算法的一种更高效的改进版本，是非稳定排序算法；希尔排序目的为了加快速度改进了插入排序，交换不相邻的元素对数组的局部进行排序，并最终用插入排序将局部有序的数组排序。

我们可以来看一个例子：

?原始数组为：[7,6,9,3,1,5,2,4]

使用希尔排序首先我们要确定一个初始增量gap，一般设为arr.length/2

1)初始增量gap=arr.length/2=4，对距离为4的数拿出来进行排序

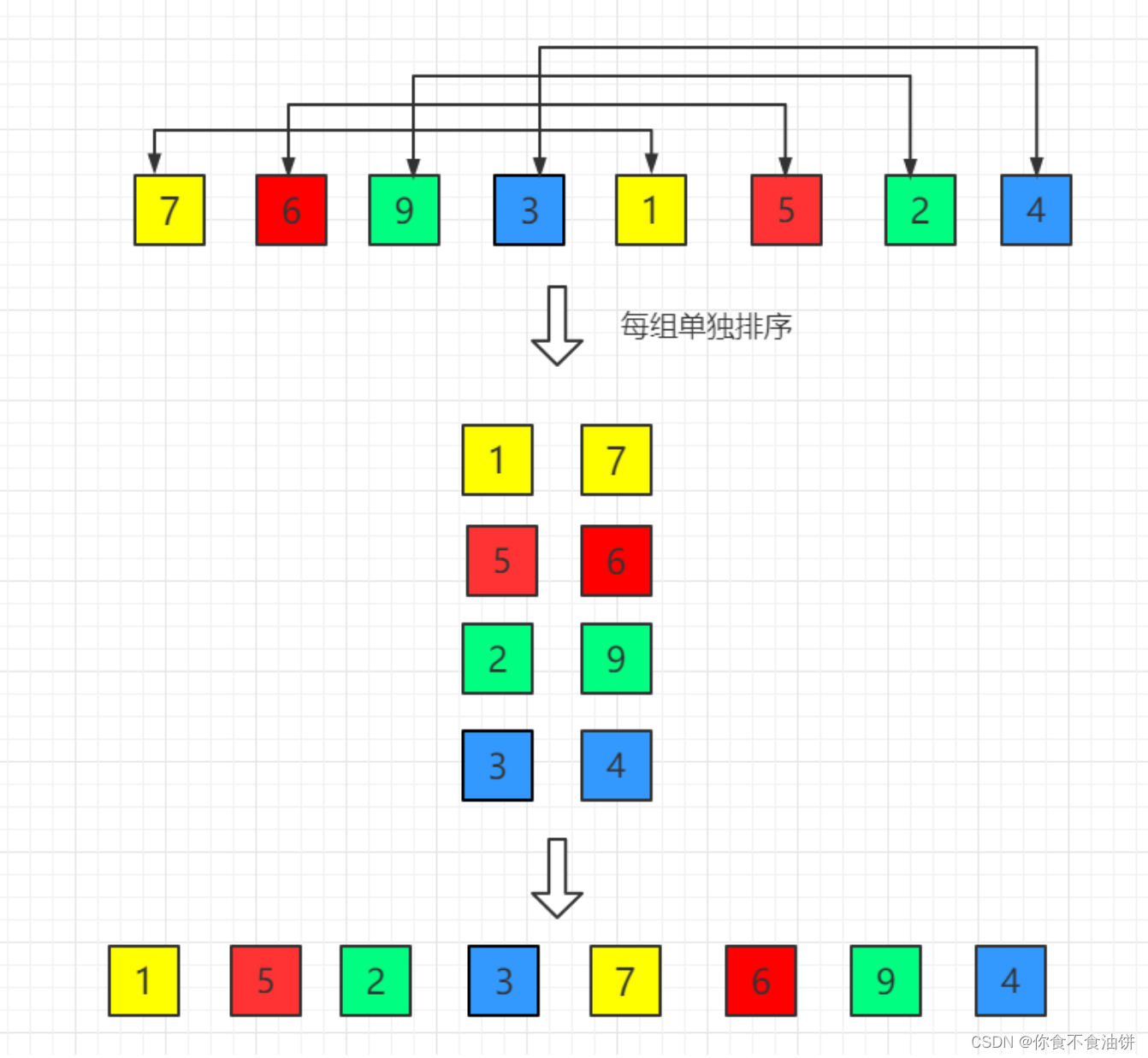
?2）增量gap=gap/2=2

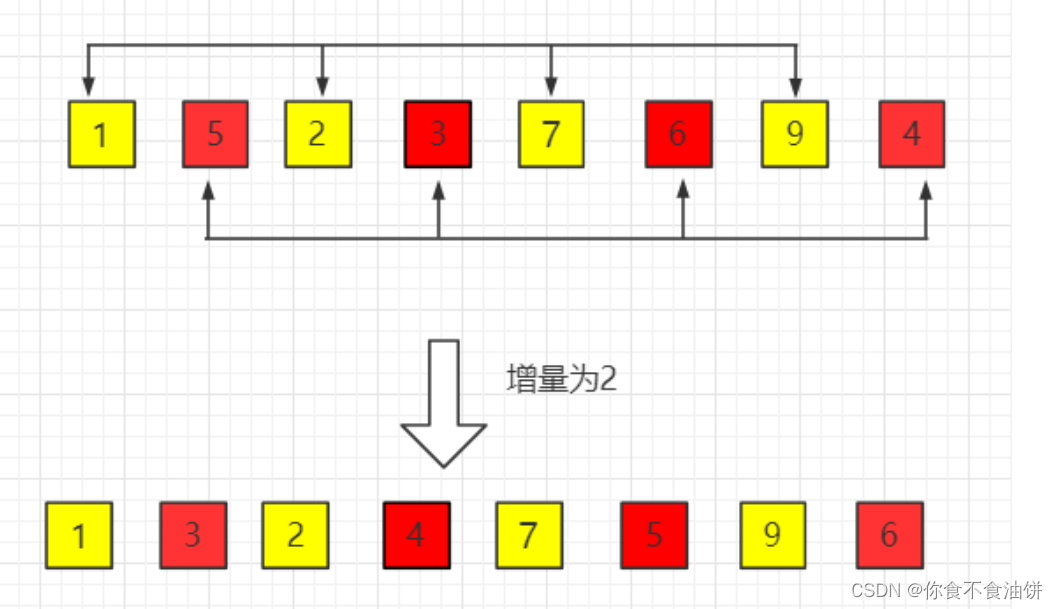
?3）gap=1，此时得到最终结果

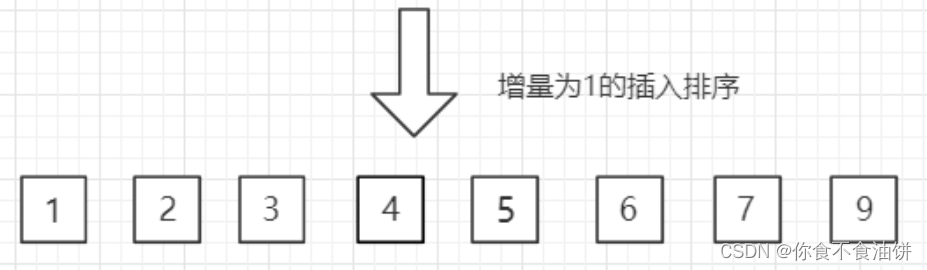
?看到这最后一步增量为1时的排序，是不是有点像插入排序，是的所以我们一般认为希尔排序就是插入排序的一种进阶版(添加了一个不断变化的gap增量)！

//希尔排序就相当于改良版的插入排序 也运用了插入排序的原理 缩小增量排序
    public static void sort2(int[] arr) {
        int count = 0;
        int j = 0; //j理解为插入排序的insertIndex
        int temp = 0; // 理解为插入排序的insertVal
        for (int gap = arr.length / 2; gap > 0; gap /= 2) {
            for (int i = gap; i < arr.length; i++) {
                temp = arr[i];
                j = i - gap;
                while (j >= 0 && temp < arr[j]) {
                    arr[j + gap] = arr[j];
                    j -= gap;
                }
                arr[j + gap] = temp;
            }
//            System.out.println("第" + (++count) + "轮的排序后的结果是" + Arrays.toString(arr) + ",步长为" + gap);
        }
    }

时间复杂度：O(n^(1.3-2))

空间复杂度：O(1)

5.快速排序(QuickSort)

快速排序是通过多次比较和交换来实现排序，在一趟排序中把将要排序的数据分成两个独立的部分，对这两部分进行排序使得其中一部分所有数据比另一部分都要小，然后继续递归排序这两部分，最终实现所有数据有序。

流程：

1. 首先设定一个分界值，一般取中间值，通过该分界值将数组分成左右两部分。?
2. 将大于或等于分界值的数据集中到数组右边，小于分界值的数据集中到数组的左边。此时，左边部分中各元素都小于分界值，而右边部分中各元素都大于或等于分界值。?
3. 然后，左边和右边的数据可以独立排序。对于左侧的数组数据，又可以取一个分界值，将该部分数据分成左右两部分，同样在左边放置较小值，右边放置较大值。右侧的数组数据也可以做类似处理。?
4. 重复上述过程，可以看出，这是一个递归定义。通过递归将左侧部分排好序后，再递归排好右侧部分的顺序。当左、右两个部分各数据排序完成后，整个数组的排序也就完成了。

快速排序思想就是这样，我建议可以看看代码能帮助我们快速理解:

public static void quickSort(int[] arr, int leftIndex, int rightIndex) {
        if (leftIndex >= rightIndex) return;
        int left = leftIndex;
        int right = rightIndex;
        //待排序的中间值作为基准值
        int key = arr[(leftIndex+rightIndex)/2];
        int temp;
        //从左右两边交替扫描，直到left = right
        while (left < right) {
            while ( arr[right] > key) {
                //从右往左扫描，找到第一个比基准值小的元素
                right--;
            }
            while (arr[left] < key) {
                //从左往右扫描，找到第一个比基准值大的元素
                left++;
            }
            //当right left移动到一个位置时 退出循环
            if (right <= left) break;
            //两边找到值后 交换值
            temp = arr[left];
            arr[left] = arr[right];
            arr[right] = temp;

//交换后发现 arr[left]==key,证明right移动到基准值才退出的while循环，即右边没有比基准值小的数
            //此时要把right--
            if (arr[left]==key) right--;
            if (arr[right] == key) left++;
        }
//        System.out.println("排序后的结果是" + Arrays.toString(arr));
        //向左递归
            quickSort(arr,leftIndex,left-1);
        //向右递归
            quickSort(arr,right+1,rightIndex);

    }

?时间复杂度：O(nlogn)

空间复杂度：O(logn)

6.归并排序(MergeSort)

归并排序是建立在归并操作上的一种有效，稳定的排序算法，该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

流程：

1. 申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列
2. 设定两个指针，最初位置分别为两个已经排序序列的起始位置
3. 比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置
4. 重复步骤3直到某一指针超出序列尾
5. 将另一序列剩下的所有元素直接复制到合并序列尾

就是典型的利用分治法，把分和治分开来，我们先来实现一下治的算法——就是两个数组进行合并成一个新数组(前提是两个有序数组)：

 public static void merge(int[] arr,int left,int mid,int right,int[] temp){

        int i = left;  //要合并的左边数组的初始索引
        int j = mid +1; //要合并的右边数组的初始索引
        int t = 0; //temp数组的初始索引

        while (i <= mid && j <= right){
            if (arr[j] < arr[i]) { //当右边索引的值小于左边的，把右边索引的值赋给temp
                temp[t] = arr[j];
                t++;
                j++;
            }else {  //反之同理
                temp[t] = arr[i];
                t++;
                i++;
            }
        }
        while ( i<= mid){ //右边数组放完了，把左边数组依次放入temp
            temp[t] = arr[i];
            t++;
            i++;
        }
        while ( j<= right){ //左边数组放完了，把右边数组依次放入temp
            temp[t] = arr[j];
            t++;
            j++;
        }

        //这时temp数组已经是合并完的数组，再把他复制回arr数组
        t =0;
        int tempLeft = left;
        while (tempLeft <= right){
            arr[tempLeft] = temp[t];
            t++;
            tempLeft++;
        }
    }

有了合并算法，我们看看怎么把分和治结合起来,这个时候我们就需要想到递归：

public static void mergeSort(int[] arr,int left,int right,int[] temp){
        if (left < right){
            int mid = (left+right)/2;
            //向左递归分解
            mergeSort(arr,left,mid,temp);
            //向右递归分解
            mergeSort(arr,mid+1,right,temp);
            //每分解一次 合并一次
            merge(arr,left,mid,right,temp);
        }
    }

时间复杂度：O(nlogn)

空间复杂度：O(n)

7.基数排序(RadixSort)

基数排序（radix sort）属于“分配式排序”（distribution sort），又称“桶子法”（bucket sort）或bin sort，顾名思义，它是透过键值的部份资讯，将要排序的元素分配至某些“桶”中，藉以达到排序的作用，基数排序法是属于稳定性的排序，其时间复杂度为O (nlog(r)m)，其中r为所采取的基数，而m为堆数，在某些时候，基数排序法的效率高于其它的稳定性排序法。

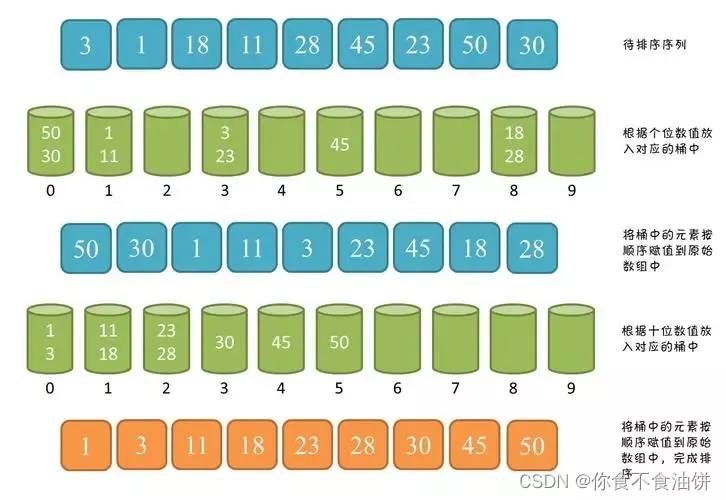
?理解这张图，基数排序首先就要分出10个桶(代表0~9）

1. 从个位数开始，根据个位数的大小进行分类，50、30放在代表为0的桶，1、11放在代表为1的桶，3、23放在代表为3的桶，45放在代表为5的桶，18、28放在代表为28的桶；
2. 分配完后，依次根据入桶的顺序出桶(先入先出)，从0~9个桶；
3. 从十位数开始，根据十位数的大小进行分类，如果没有10位数就视为0，放在代表为0的桶；
4. 分配完后，继续依次根据如同的顺序出桶(先入先出)，从0~9个桶；
5. 发现没有百位数，遍历结束，得到最终结果；

我们可以看看代码：

public static void radixSort(int[] arr){
        //位数0~9就分为10个桶,每个桶装的数不确定，最大为arr.length
        int[][] bucket = new int[10][arr.length];
        //用一个数组来定义每个桶的装的数据个数
        int[] bucketCounts = new int[10];

        int count = 1;
        int max = arr[0];
        //找出最大数，方便定义循环次数
        for (int i = 1; i < arr.length; i++) {
            if (max < arr[i]) max = arr[i];
        }
        //入桶
        for (int k = 1; k < max; k *= 10 ) {
            for (int i = 0; i < arr.length; i++) {
                int digitOfElement = arr[i] / k % 10;
                //每个桶装的数据个数初始为0，装了一个之后就加一
                bucket[digitOfElement][bucketCounts[digitOfElement]] = arr[i];
                bucketCounts[digitOfElement]++;
            }
            //用一个index来表示新的arr数组索引
            int index = 0;
            //分完之后，把每个桶的数据依次放到arr数组中
            //遍历每个桶
            for (int i = 0; i < 10; i++) {
                //当该桶有数据时，才进行赋值
                if (bucketCounts[i] != 0) {
                    //遍历桶里装的数据个数
                    for (int j = 0; j < bucketCounts[i]; j++) {
                        arr[index++] = bucket[i][j];
                    }
                }
                bucketCounts[i] = 0;  //每次都会把桶数据清0
            }
//            System.out.println("第"+(count++)+"轮排序后" + Arrays.toString(arr));
        }
    }

?时间复杂度：O(k*n) k为最高位数，n为元素个数

空间复杂度：O(10*length)

总结：这七大基本排序算法一直都是面试笔试的常考题，建议大家能熟练于心，另外博主会持续更新算法知识，希望小伙伴们可以关注我哦~