希尔排序
插入排序存在的问题:当需要插入的数是较小的数时,后移的次数明显增多,排序效率受到影响。为解决这一问题,希尔于1959年提出了一种排序算法。希尔排序是简单插入排序经过改进之后的一个更高效的版本,也被称为缩小增量排序。
基本思想:希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至1时,整个文件恰好被分成一组,算法终止。
分组 ==>?简单插入排序 ==>?缩小增量 ==>?分组 ==>?简单插入排序 ==>?缩小增量......
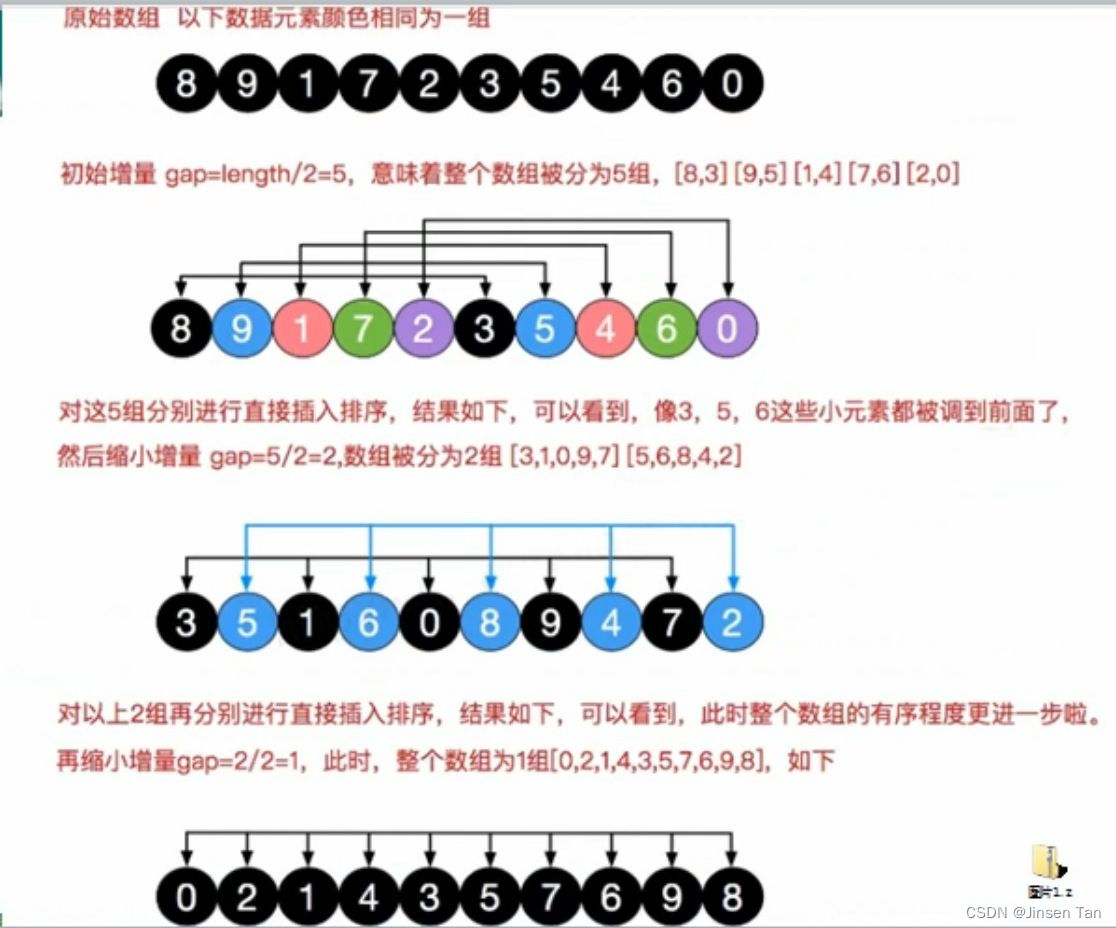
?代码实现:
package sort;
import java.text.SimpleDateFormat;
import java.util.Arrays;
import java.util.Date;
public class ShellSort {
public static void main(String[] args) {
int[] arr = new int[80000];
for (int i = 0; i < 80000; i++) {
arr[i] = (int)(Math.random()*80000);//生成[0,80000)随机数
}
System.out.print("希尔排序之前:");
Date date1 = new Date();
SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
String date1Str = simpleDateFormat.format(date1);
System.out.println(date1Str);
shellSort(arr);
System.out.print("希尔排序之后:");
Date date2 = new Date();
String date2Str = simpleDateFormat.format(date2);
System.out.println(date2Str);
//int[] arr = { 8,9,1,7,2,3,5,4,6,0};
//shellSort(arr);
int[] arr2 = new int[80000];
for (int i = 0; i < 80000; i++) {
arr2[i] = (int)(Math.random()*80000);//生成[0,80000)随机数
}
System.out.print("优化版希尔排序之前:");
Date date11 = new Date();
String date11Str = simpleDateFormat.format(date2);
System.out.println(date11Str);
shellSort2(arr2);
System.out.print("优化版希尔排序之后:");
Date date22 = new Date();
String date22Str = simpleDateFormat.format(date22);
System.out.println(date22Str);
}
//交换法 or 移动法
//交换法
public static void shellSort(int[] arr){
/*
//使用逐步推导法编写希尔排序
//希尔排序第1轮排序
//因为第1轮排序,是将10个数据分成了5组
int temp = 0;
for (int i = 5; i < arr.length; i++) {
//遍历各组中所有的元素(共5组,每组有 10/5=2 个元素)
//步长为5
for (int j = i-5; j >=0 ; j -= 5) {
//如果当前元素大于加上步长后的那个元素,则这两个元素需要交换
if (arr[j] > arr[j+5]){
temp = arr[j];
arr[j] = arr[j+5];
arr[j+5] = temp;
}
}
}
System.out.println("希尔排序第 1 轮排序结果" + Arrays.toString(arr));
//希尔排序第2轮排序
//因为第2轮排序,是将10个数据分成了 5/2=2 组
for (int i = 2; i < arr.length; i++) {
//遍历各组中所有的元素(共 5/2=2 组,每组有 10/5=2 个元素)
//步长为5
for (int j = i-2; j >=0 ; j -= 2) {
//如果当前元素大于加上步长后的那个元素,则这两个元素需要交换
if (arr[j] > arr[j+2]){
temp = arr[j];
arr[j] = arr[j+2];
arr[j+2] = temp;
}
}
}
System.out.println("希尔排序第 2 轮排序结果" + Arrays.toString(arr));
//希尔排序第3轮排序
//因为第轮排序,是将10个数据分成了 5/2/2=1 组
for (int i = 1; i < arr.length; i++) {
//遍历各组中所有的元素(共 5/2/2=1 组,每组有 10/5/2=1 个元素)
//步长为5
for (int j = i-1; j >=0 ; j --) {
//如果当前元素大于加上步长后的那个元素,则这两个元素需要交换
if (arr[j] > arr[j+1]){
temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
System.out.println("希尔排序第 3 轮排序结果" + Arrays.toString(arr));
*/
//根据前面的分析,使用循环处理
int count = 0;
for (int gap = arr.length/2; gap > 0; gap /=2){
for (int i = gap; i < arr.length; i++) {
//遍历各组中所有的元素(共 gap 组,每组有 arr.length/gap 个元素)
//步长为gap
for (int j = i - gap; j >=0 ; j -= gap) {
//如果当前元素大于加上步长后的那个元素,则这两个元素需要交换
if (arr[j] > arr[j+gap]){
int temp = arr[j];
arr[j] = arr[j+gap];
arr[j+gap] = temp;
}
}
}
//System.out.println("希尔排序第" + (++count) + "轮的排序结果:" + Arrays.toString(arr));
}
}
//对交换式的希尔排序进行优化 ——>移位法
public static void shellSort2(int[] arr){
//增量gap,并逐步缩小增量
for (int gap = arr.length/2; gap > 0; gap /= 2){
//从第gap个元素,逐个对其所在的组进行直接插入排序
for (int i = gap; i < arr.length; i++) {
int j = i;
int temp = arr[j];
if (arr[j] < arr[j-gap]){
while (j - gap >= 0 && temp < arr[j-gap]){
//移动
arr[j] = arr[j-gap];
j -= gap;
}
//退出while循环后,给temp找到插入位置
arr[j] = temp;
}
}
}
}
}
快速排序
基本思想:快速排序是对冒泡排序的一种改进,其基本思想就是通过一趟排序将要排序的数据分割成独立的两个部分,其中一部分的所有数据都比另外一部分的所有数据要小。然后,按此方法对这两个部分数据分别进行快速排序,整个排序过程可以递归进行,以达到整个数据变成有序序列。
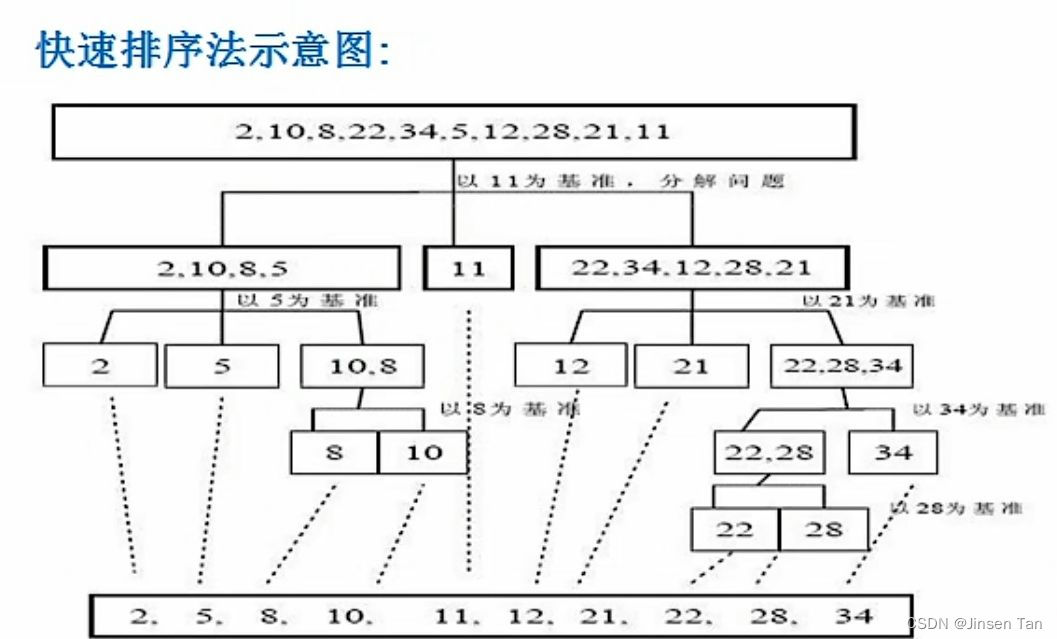
?基准的选择可以随机
代码实现:
package sort;
import java.text.SimpleDateFormat;
import java.util.Arrays;
import java.util.Date;
public class QuickSort {
public static void main(String[] args) {
//int[] arr = { 6,4,7,5,8,1,2,36,4,78,-4,4,5,-8,-6,35,75};
//System.out.println(Arrays.toString(arr));
//quickSort(arr,0, arr.length-1);
//System.out.println(Arrays.toString(arr));
int[] arr = new int[8000000];
for (int i = 0; i < 8000000; i++) {
arr[i] = (int)(Math.random()*8000000);//生成[0,8000000)随机数
}
System.out.print("快速排序之前:");
Date date1 = new Date();
SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
String date1Str = simpleDateFormat.format(date1);
System.out.println(date1Str);
quickSort(arr,0, arr.length - 1);
System.out.print("快速排序之后:");
Date date2 = new Date();
String date2Str = simpleDateFormat.format(date2);
System.out.println(date2Str);
int[] arr2 = new int[80000];
for (int i = 0; i < 80000; i++) {
arr2[i] = (int)(Math.random()*80000);//生成[0,80000)随机数
}
System.out.print("简化版快速排序之前:");
Date date11 = new Date();
String date11Str = simpleDateFormat.format(date2);
System.out.println(date11Str);
quickSort2(arr2,0, arr2.length - 1);
System.out.print("简化版快速排序之后:");
Date date22 = new Date();
String date22Str = simpleDateFormat.format(date22);
System.out.println(date22Str);
}
public static void quickSort(int[] arr,int low, int high){
int left = low;
int right = high;
//pivot 中轴值
int pivot = arr[(left + right) / 2];
//while循环的目的是让比pivot小的值放到左边
//比pivot大的值放到右边
while (left < right){
//在pivot的左边一直找,找到大于等于pivot的值,才退出
while (arr[left] < pivot) left++;
//在pivot的右边一直找,找到小于pivot的值,才退出
while (arr[right] > pivot) right--;
//如果left >= right说明pivot的左右两边的值,已经按照左边全部是
//小于pivot的值,右边全部是大于等于pivot的值
if (left >= right){
break;
}
//交换
int temp = arr[left];
arr[left] = arr[right];
arr[right] = temp;
//如果交换完毕后,发现arr[left] == pivot,则right前移
if (arr[left] == pivot) right--;
//如果交换完毕后,发现arr[right] == pivot,则left后移
if (arr[right] == pivot) left++;
}
//如果 left == right ,必须left++,right--,否则会栈溢出
if (left == right){
left++;
right--;
}
//向左递归
if (left < high) quickSort(arr,left,high);
//向右递归
if (right > low) quickSort(arr,low,right);
}
//简化版本
public static void quickSort2(int[] arr, int low, int high){
if (low >= high)
return;
int i = low;
int j = high;
int temp = arr[low];
while (i < j){
while (arr[j] >= temp && i < j) j--;
while (arr[i] <= temp && i < j) i++;
if (i < j){
int Temp = arr[i];
arr[i] = arr[j];
arr[j] = Temp;
}
}
arr[low] = arr[i];
arr[i] = temp;
quickSort(arr,low,i-1);
quickSort(arr,i+1,high);
}
}
归并排序
归并排序是利用归并的思想实现的排序方法,该算法采用经典的分治策略(分治法将问题 “分” 成一些小问题递归求解,“治”?的阶段则将 “分”?的阶段得到的答案修补在一起,即分而治之。)。
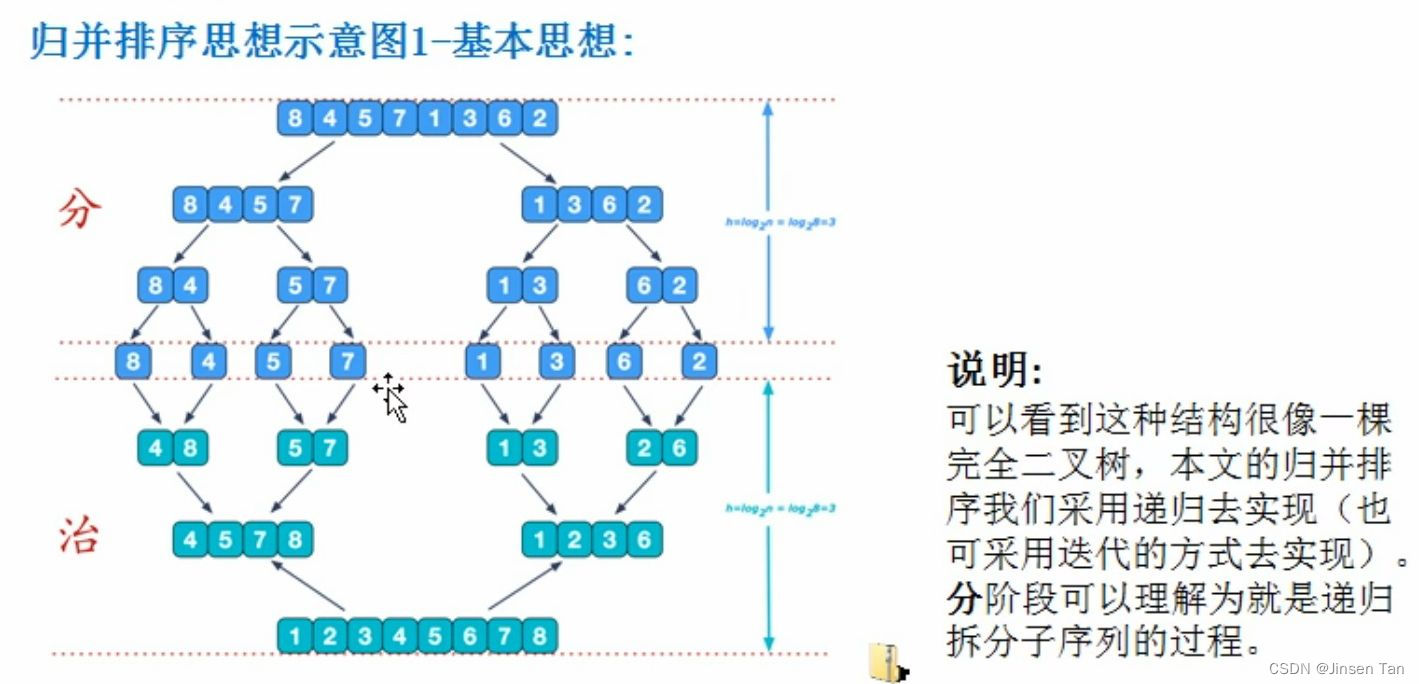
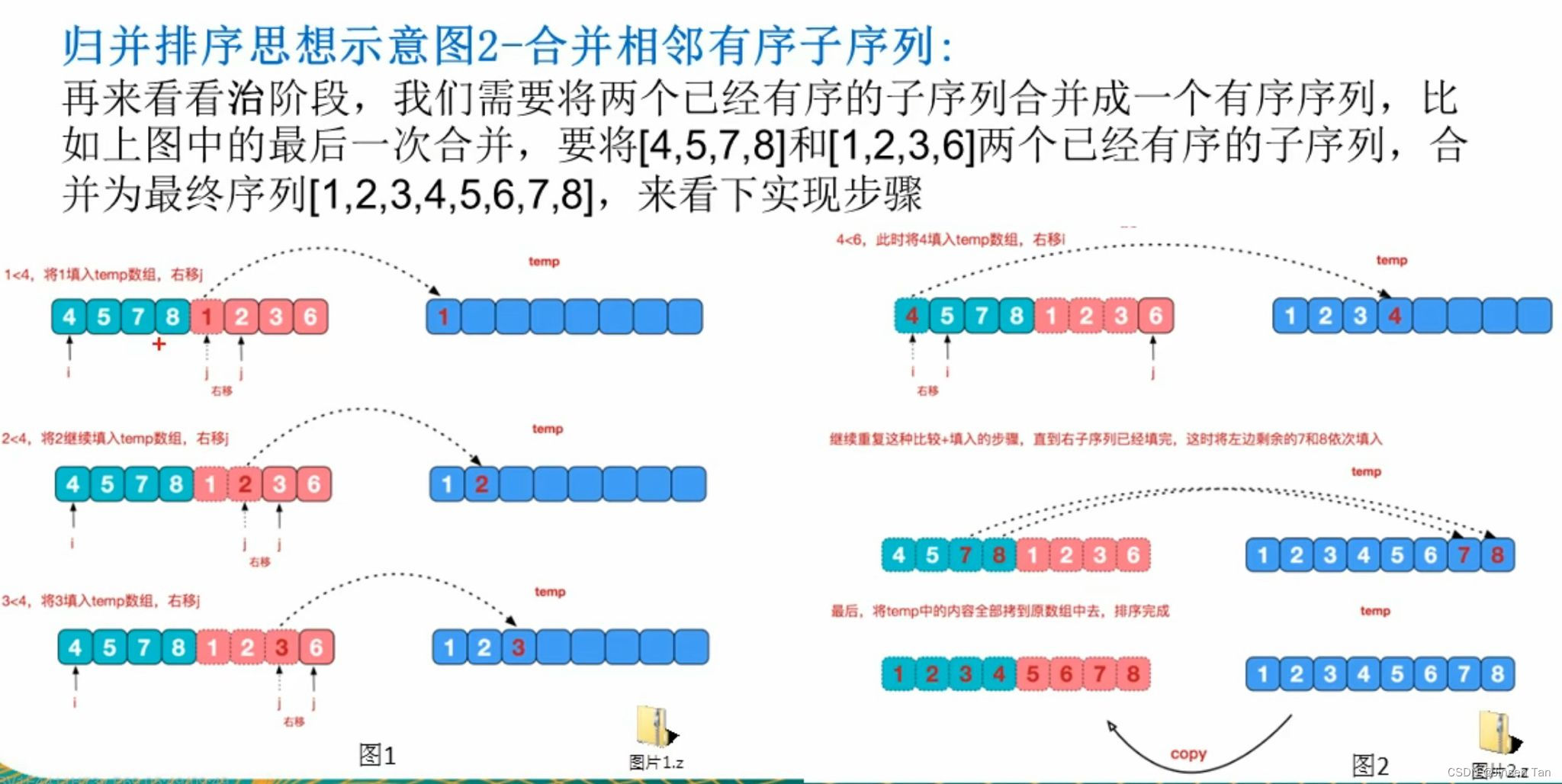
合并的步骤:
1.? 先把左右两边有序的数据按照规则填充到temp数组,直到左右两边的有序序列有一边处理完毕为止;
2.?把未处理完毕的一边的数据依次全部填充到temp;
3.?将temp中的元素拷贝到arr。//注意:并不是每一次都拷贝所有元素
代码实现:
package sort;
import java.text.SimpleDateFormat;
import java.util.Arrays;
import java.util.Date;
public class MergeSort {
public static void main(String[] args) {
/*int[] arr = { 8,4,5,7,1,3,6,2 };
int[] temp = new int[arr.length];//归并排序需要额外的存储空间
mergeSort(arr,0, arr.length - 1,temp);
System.out.println("归并排序后=" + Arrays.toString(arr));
*/
int[] arr = new int[8000000];
for (int i = 0; i < 8000000; i++) {
arr[i] = (int)(Math.random()*8000000);//生成[0,80000)随机数
}
int[] temp = new int[arr.length];
System.out.print("归并排序之前:");
Date date1 = new Date();
SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
String date1Str = simpleDateFormat.format(date1);
System.out.println(date1Str);
mergeSort(arr,0, arr.length - 1,temp );
System.out.print("归并排序之后:");
Date date2 = new Date();
String date2Str = simpleDateFormat.format(date2);
System.out.println(date2Str);
}
//归并排序 = 分 + 合
//分+合方法
public static void mergeSort(int[] arr, int left, int right, int[] temp){
if (left < right){
int mid = (right + left)/2;//中间索引
//向左递归进行分解
mergeSort(arr,left,mid,temp);
//向右递归进行分解
mergeSort(arr,mid+1,right,temp);
//到合并时
merge(arr,left,mid,right,temp);
}
}
//合并的方法
public static void merge(int[] arr, int left, int mid, int right, int[] temp){
/*
arr 排序的原始数组
left 左边有序序列的初始索引
mid 中间索引,右边有序序列的初始索引
right 右边有序序列的末序列
temp 中转数组
*/
int i = left; //初始化 i ,左边有序序列的初始索引
int j = mid + 1;//初始化 j ,右边有序序列的初始索引
int t = 0;//指向temp数组的当前索引
/*
(一)
先把左右两边有序的数据按照规则填充到temp数组
直到左右两边的有序序列,有一边处理完毕为止
*/
while (i <= mid && j <= right){
//如果左右有序序列的当前元素小于等于右边有序序列当前的元素
//则将左边的当前元素,填充到temp数组
//然后t++,i++ 索引后移
if (arr[i] <= arr[j]){
temp[t] = arr[i];
t++;
i++;
}else {//反之,将右边的当前元素,填充到temp数组
temp[t] = arr[j];
t++;
j++;
}
}
/*
(二)
把未处理完毕的一边的数据依次全部填充到temp
*/
while ( i <= mid ){//左边的有序序列还有剩余元素,就全部填充到temp数组
temp[t] = arr[i];
t++;
i++;
}
while ( j <= right){
temp[t] = arr[j];
t++;
j++;
}
/*
(三)
将temp数组中的元素拷贝到arr
注意:并不是每一次都拷贝所有元素
*/
t = 0;
int tempLeft = left;
while (tempLeft <= right){
//第一次合并时tempLeft = 0,right = 1 // tempLeft = 2 right = 3 //
//最后一次合并时,tempLeft= 7, right= 7
arr[tempLeft] = temp[t];
tempLeft++;
t++;
}
}
}
基数排序(桶排序)
基数排序属于 “分配式”?排序,又称 “桶子法” (bucket?sort?or?bin?sort),顾名思义,它是通过键值的各个位的值,将要排序的元素分配到某些 “桶” 中,达到排序的目的。基数排序是1887年赫尔曼?何乐礼发明的,它通过将整数按位数切割成不同的数字,然后按每个位数分别比较。基数排序是效率高的稳定性排序。
基本思想:将所有待比较数值统一为同样的数位长度,数位较短的数前面补零。然后,从最低位开始,依次进行一次排序。这样从最低位排序一直到最高位排序完成以后,数列就变成了一个有序序列。
注意:基数排序是典型的空间换时间的算法,占用内存很大,当对海量数据排序时,容易造成 OutOfMemoryError。
注意:有负数的数组,我们一般不使用基数排序进行排序。
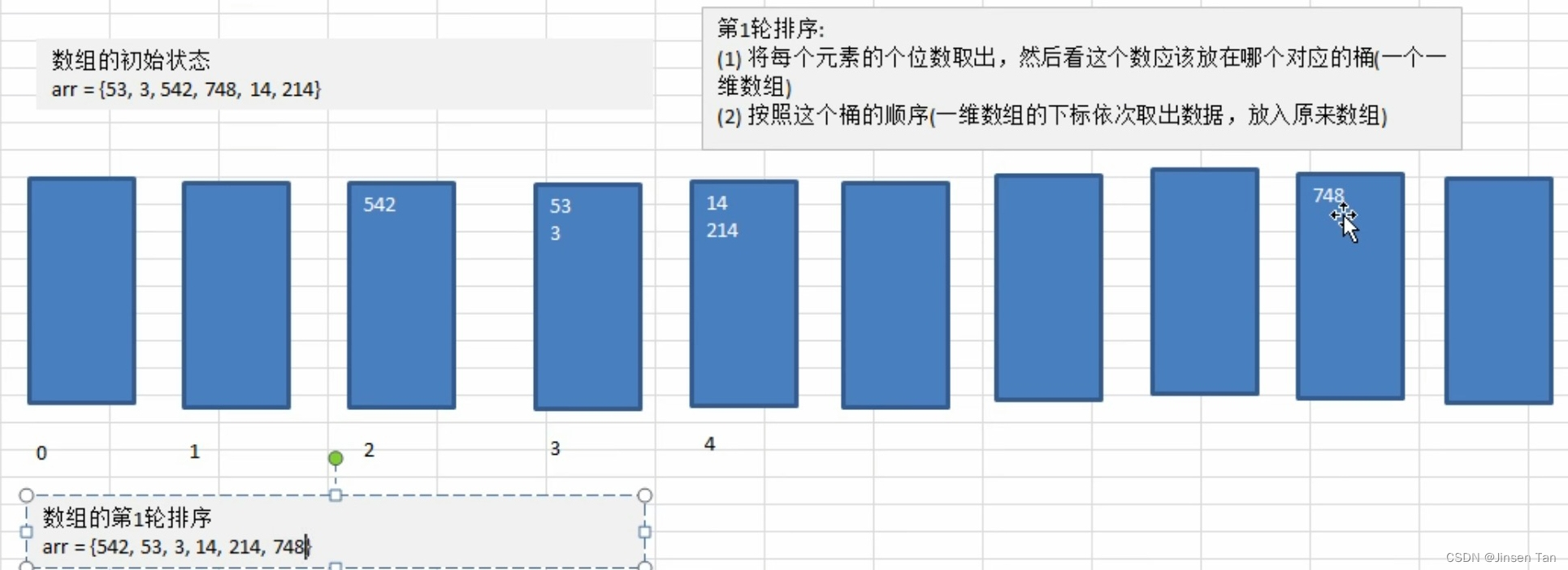
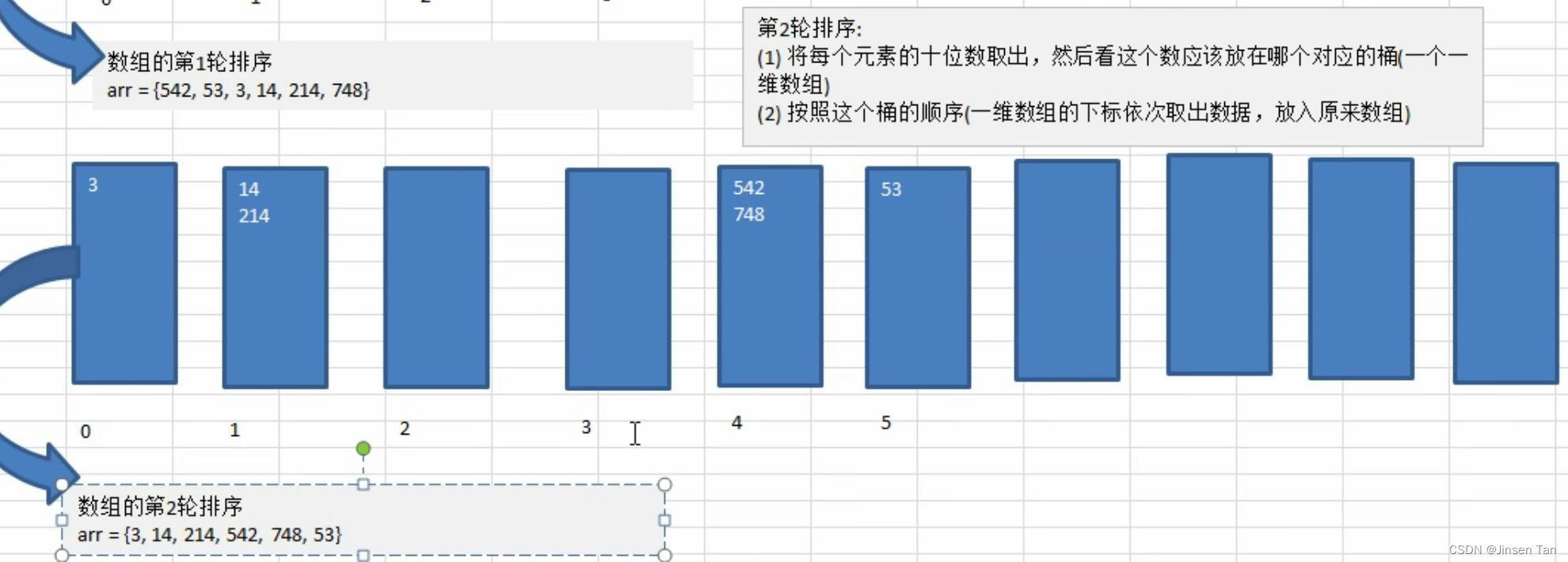
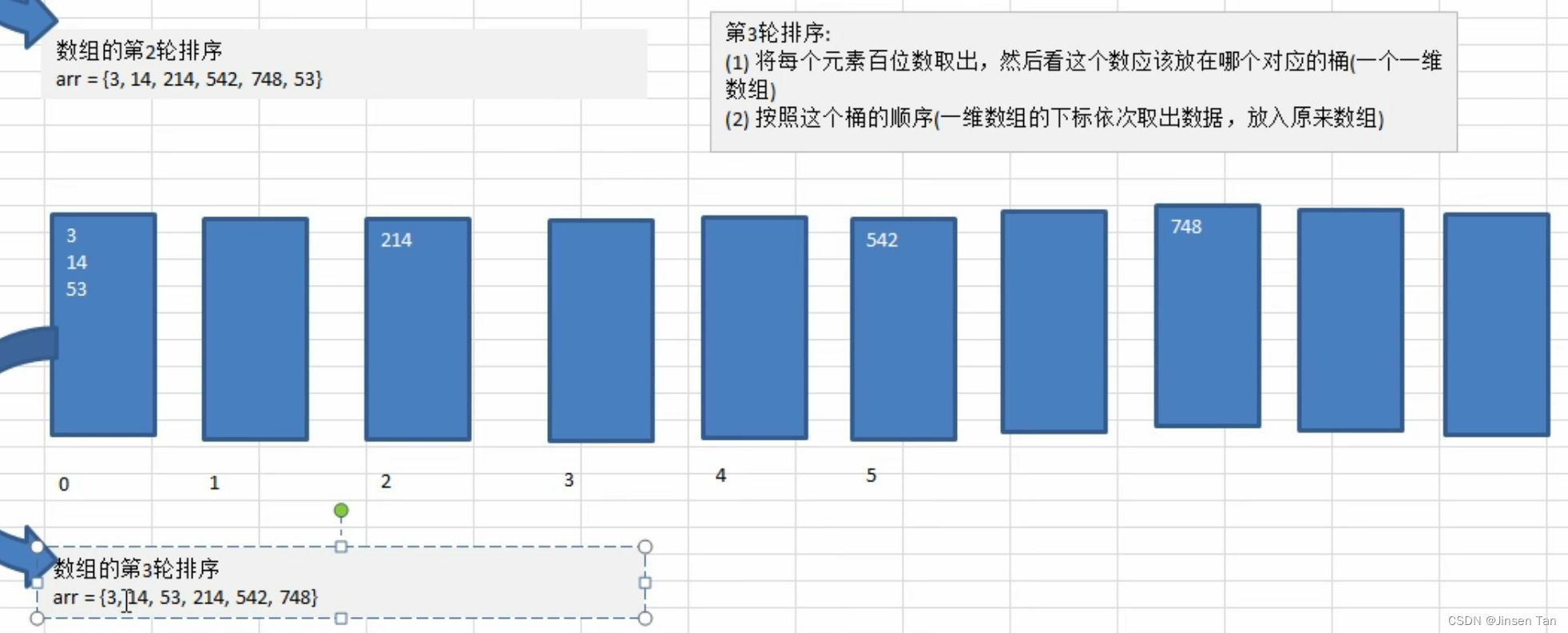
代码实现:
package sort;
import java.text.SimpleDateFormat;
import java.util.Arrays;
import java.util.Date;
public class RadixSort {
public static void main(String[] args) {
/*int[] arr = { 53, 3, 542, 748, 14, 214 };
System.out.println("基数排序前=" + Arrays.toString(arr));
radixSort(arr);
System.out.println("基数排序后=" + Arrays.toString(arr));
*/
int[] arr = new int[8000000];
for (int i = 0; i < 8000000; i++) {
arr[i] = (int)(Math.random()*8000000);//生成[0,80000)随机数
}
int[] temp = new int[arr.length];
System.out.print("基数排序之前:");
Date date1 = new Date();
SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
String date1Str = simpleDateFormat.format(date1);
System.out.println(date1Str);
radixSort(arr);
System.out.print("基数排序之后:");
Date date2 = new Date();
String date2Str = simpleDateFormat.format(date2);
System.out.println(date2Str);
}
//基数排序
public static void radixSort(int[] arr){
/*===================推导过程=================
//第 1 轮排序,即针对每个元素的个位进行排序处理
//定义一个二维数组,表示 10 个桶,每个桶就是一个一维数组
//说明:
//1. 二维数组包含 10 个一维数组
//2. 为了防止放数时数据溢出,则每个一维数组的大小定为 arr.length
//3. 基数排序是典型的使用空间换时间的算法
int[][] bucket = new int[10][arr.length];
//为了记录每个桶中,实际放了多少个数据,定义一个一维数组来记录各个桶的每次放入的数据个数
//注:bucketElementCounts[0] ,记录的就是 bucket[0] 桶放入数据的个数
int[] bucketElementCounts = new int[10];
//第 1 轮,针对每个元素的个位进行排序处理
for (int i = 0; i < arr.length; i++) {
// 取出每个元素的个位数
int digitOfElement = arr[i] /10 % 10;
//放到对应的桶中
bucket[digitOfElement][bucketElementCounts[digitOfElement]] = arr[i];
bucketElementCounts[digitOfElement]++;
}
//按照这个桶的书序(一维数组的下标依次取出数据,放入原来的数组)
int index = 0;
//遍历每一个桶,并将桶中的数据放入到原数组
for (int j = 0; j < bucketElementCounts.length; j++) {
//如果桶中有数据,则放回到原数组
if (bucketElementCounts[j] != 0){
//循环该桶(即第 k 个桶,第 k 个一维数组),放入数据
for (int k = 0; k < bucketElementCounts[j]; k++) {
//取出元素,放入到原数组 arr
arr[index++] = bucket[j][k];
}
}
//!!!!!!第 1 轮处理后,需要将每个 bucketElementCounts[j] = 0!!!!!!!
bucketElementCounts[j] = 0;
}
System.out.println("第 1 轮对个位数的排序处理 arr = " + Arrays.toString(arr));
//=====================================================================
//第 2 轮,针对每个元素的十位进行排序处理
for (int i = 0; i < arr.length; i++) {
// 取出每个元素的十位数
int digitOfElement = arr[i] /10 % 10;
//放到对应的桶中
bucket[digitOfElement][bucketElementCounts[digitOfElement]] = arr[i];
bucketElementCounts[digitOfElement]++;
}
//按照这个桶的书序(一维数组的下标依次取出数据,放入原来的数组)
index = 0;
//遍历每一个桶,并将桶中的数据放入到原数组
for (int j = 0; j < bucketElementCounts.length; j++) {
//如果桶中有数据,则放回到原数组
if (bucketElementCounts[j] != 0){
//循环该桶(即第 k 个桶,第 k 个一维数组),放入数据
for (int k = 0; k < bucketElementCounts[j]; k++) {
//取出元素,放入到原数组 arr
arr[index++] = bucket[j][k];
}
}
//!!!!!!第 2 轮处理后,需要将每个 bucketElementCounts[j] = 0!!!!!!!
bucketElementCounts[j] = 0;
}
System.out.println("第 2 轮对个位数的排序处理 arr = " + Arrays.toString(arr));
//=====================================================================
//第 3 轮,针对每个元素的百位进行排序处理
for (int i = 0; i < arr.length; i++) {
// 取出每个元素的百位数
int digitOfElement = arr[i] /100 % 10;
//放到对应的桶中
bucket[digitOfElement][bucketElementCounts[digitOfElement]] = arr[i];
bucketElementCounts[digitOfElement]++;
}
//按照这个桶的书序(一维数组的下标依次取出数据,放入原来的数组)
index = 0;
//遍历每一个桶,并将桶中的数据放入到原数组
for (int j = 0; j < bucketElementCounts.length; j++) {
//如果桶中有数据,则放回到原数组
if (bucketElementCounts[j] != 0){
//循环该桶(即第 k 个桶,第 k 个一维数组),放入数据
for (int k = 0; k < bucketElementCounts[j]; k++) {
//取出元素,放入到原数组 arr
arr[index++] = bucket[j][k];
}
}
}
System.out.println("第 3 轮对个位数的排序处理 arr = " + Arrays.toString(arr));
*/
//========================实现过程=======================
int[][] bucket = new int[10][arr.length];
//为了记录每个桶中,实际放了多少个数据,定义一个一维数组来记录各个桶的每次放入的数据个数
//注:bucketElementCounts[0] ,记录的就是 bucket[0] 桶放入数据的个数
int[] bucketElementCounts = new int[10];
//根据前面的推导过程,可以得到基数排序的最终代码
//得到数组中最大的数的位数
int max = arr[0];
for (int i = 1; i < arr.length; i++) {
if (arr[i] > max)
max = arr[i];
}
//得到最大的数是几位数
int maxLength = (max + "").length();
for (int i = 0,n = 1; i < maxLength; i++, n *= 10) {
//第 i+1 轮,针对每个元素的对应位进行排序处理
for (int j = 0; j < arr.length; j++) {
// 取出每个元素的个位数
int digitOfElement = arr[j] /n % 10;
//放到对应的桶中
bucket[digitOfElement][bucketElementCounts[digitOfElement]] = arr[j];
bucketElementCounts[digitOfElement]++;
}
//按照这个桶的书序(一维数组的下标依次取出数据,放入原来的数组)
int index = 0;
//遍历每一个桶,并将桶中的数据放入到原数组
for (int k = 0; k < bucketElementCounts.length; k++) {
//如果桶中有数据,则放回到原数组
if (bucketElementCounts[k] != 0){
//循环该桶(即第 k 个桶,第 k 个一维数组),放入数据
for (int l = 0; l < bucketElementCounts[k]; l++) {
//取出元素,放入到原数组 arr
arr[index++] = bucket[k][l];
}
}
//!!!!!!第 i+1 轮处理后,需要将每个 bucketElementCounts[k] = 0!!!!!!!
bucketElementCounts[k] = 0;
}
//System.out.println("第"+ (i+1) +"轮对个位数的排序处理 arr = " + Arrays.toString(arr));
}
}
}
常用排序算法对比及解释
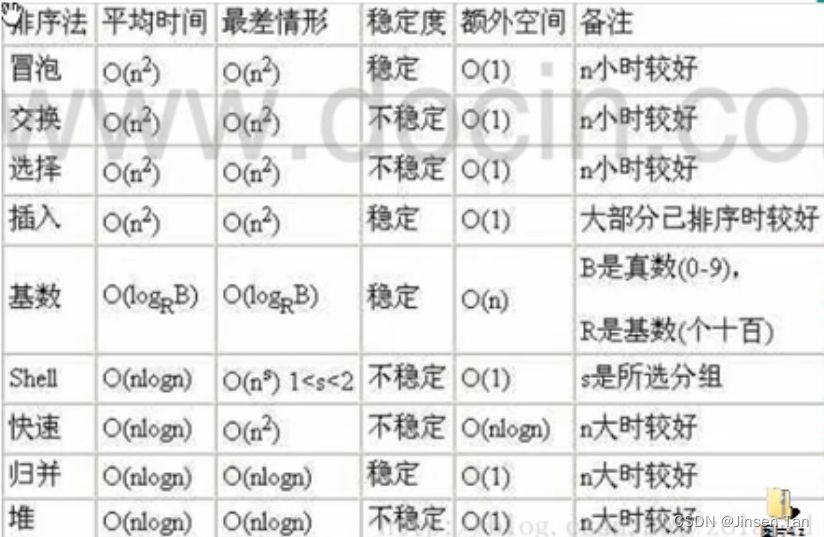
稳定:如果 a?原本在 b?的前面且 a = b ,排序之后 a?仍然在 b?的前面;
不稳定:如果 a?原本在 b?的前面且 a = b ,排序之后 a?可能不在 b?的前面;
内排序:所有排序操作都在内存中完成;
外排序:由于数据过大,因此把数据放在磁盘中,而排序要通过磁盘和内存的数据传输才能进行;
时间复杂度:一个算法执行所耗费的时间;
空间复杂度:运行完一个程序所需的内存大小
排序算法代码汇总:
package sort;
import java.util.Arrays;
public class Sort {
public static void main(String[] args) {
int[] arr1 = { 1,9,5,1,2,4,7,-4,-2,14,69,7,5 };
int[] arr2 = { 9,4,7,4,5,7,-4,5,675,8,4,-36,-12,35};
int[] arr3 = { 6,4,7,5,8,1,2,36,4,78,-4,4,5,-8,-6,35,75};
int[] arr4 = { 8,9,1,7,2,3,5,4,6,0};
int[] arr5 = { 8,9,1,7,2,3,5,4,6,0};
int[] arr6 = { 6,4,7,5,8,1,2,36,4,78,-4,4,5,-8,-6,35,75};
int[] arr7 = { 8,9,1,7,2,3,5,4,6,0 };
int[] temp = new int[arr7.length];
int[] arr8 = { 53, 3, 542, 748, 14, 214 };
System.out.print("冒泡排序前:");
System.out.println(Arrays.toString(arr1));
bubbleSort(arr1);
System.out.print("冒泡排序后:");
System.out.println(Arrays.toString(arr1));
System.out.print("选择排序前:");
System.out.println(Arrays.toString(arr2));
selectSort(arr2);
System.out.print("选择排序后:");
System.out.println(Arrays.toString(arr2));
System.out.print("插入排序前:");
System.out.println(Arrays.toString(arr3));
insertSort(arr3);
System.out.print("插入排序后:");
System.out.println(Arrays.toString(arr3));
System.out.print("希尔排序前:");
System.out.println(Arrays.toString(arr4));
shellSort(arr4);
System.out.print("希尔排序后:");
System.out.println(Arrays.toString(arr4));
System.out.print("优化版希尔排序前:");
System.out.println(Arrays.toString(arr5));
shellSort2(arr5);
System.out.print("优化版希尔排序后:");
System.out.println(Arrays.toString(arr5));
System.out.print("快速排序前:");
System.out.println(Arrays.toString(arr6));
quickSort(arr6,0, arr6.length - 1);
System.out.print("快速排序后:");
System.out.println(Arrays.toString(arr6));
System.out.print("归并排序前:");
System.out.println(Arrays.toString(arr7));
mergeSort(arr7,0, arr7.length-1,temp);
System.out.print("归并排序后:");
System.out.println(Arrays.toString(arr7));
System.out.print("基数排序前:");
System.out.println(Arrays.toString(arr8));
radixSort(arr8);
System.out.print("基数排序后:");
System.out.println(Arrays.toString(arr8));
}
public static void bubbleSort(int[] arr){
for (int i = 0; i < arr.length-1; i++) {
boolean flag = false;//优化
for (int j = 0; j < arr.length-1; j++) {
if (arr[j] > arr[j+1]){
int temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
flag = true;
}
}
if (!flag)
break;
}
}
public static void selectSort(int[] arr){
for (int i = 0; i < arr.length-1; i++) {
int min = arr[i];
int minIndex = i;
for (int j = i+1; j < arr.length; j++) {
if (min > arr[j]){
min = arr[j];
minIndex = j;
}
}
if (i != minIndex){
arr[minIndex] = arr[i];
arr[i] = min;
}
}
}
public static void insertSort(int[] arr){
for (int i = 1; i < arr.length; i++) {
int insertIndex = i-1;
int insertValue = arr[i];
while (insertIndex >= 0 && insertValue < arr[insertIndex]){
arr[insertIndex+1] = arr[insertIndex];
insertIndex--;
}
arr[insertIndex+1] = insertValue;
}
}
public static void shellSort(int[] arr){
for (int gap = arr.length/2; gap > 0; gap /= 2){
for (int i = gap; i < arr.length; i++) {
for (int j = i - gap; j >=0 ; j -= gap) {
if (arr[j] > arr[j+gap]) {
int temp = arr[j];
arr[j] = arr[j + gap];
arr[j + gap] = temp;
}
}
}
}
}
public static void shellSort2(int[] arr){
for (int gap = arr.length/2; gap > 0; gap /= 2){
for (int i = gap; i < arr.length; i++) {
int j = i;
int temp = arr[j];
if (arr[j] < arr[j - gap]){
while (j - gap >= 0 && temp < arr[j - gap]){
arr[j] = arr[j - gap];
j -= gap;
}
}
arr[j] = temp;
}
}
}
public static void quickSort(int[] arr, int low, int high){
if (low >= high)
return;
int i = low;
int j = high;
int temp = arr[low];
while (i < j){
while (arr[j] >= temp && i < j) j--;
while (arr[i] <= temp && i < j) i++;
if (i < j){
int Temp = arr[i];
arr[i] = arr[j];
arr[j] = Temp;
}
}
arr[low] = arr[i];
arr[i] = temp;
quickSort(arr,low,i-1);
quickSort(arr,i+1,high);
}
//归并排序
public static void mergeSort(int[] arr,int left,int right,int[] temp){
if (left < right){
int mid = (left + right)/2;
mergeSort(arr,left,mid,temp);
mergeSort(arr,mid + 1,right,temp);
merge(arr,left,mid,right,temp);
}
}
public static void merge(int[] arr, int left, int mid, int right, int[] temp){
int i = left;
int j = mid +1;
int t = 0;
while (i <= mid && j <= right){
if (arr[i] < arr[j]){
temp[t] = arr[i];
t++;
i++;
}else {
temp[t] = arr[j];
t++;
j++;
}
}
while (i <= mid){
temp[t] = arr[i];
t++;
i++;
}
while (j <= right){
temp[t] = arr[j];
t++;
j++;
}
t = 0;
int tempLeft = left;
while (tempLeft <= right){
arr[tempLeft] = temp[t];
t++;
tempLeft++;
}
}
public static void radixSort(int[] arr){
int[][] bucket = new int[10][arr.length];
int[] bucketElementCounts = new int[10];
int max = arr[0];
for (int i = 1; i < arr.length; i++) {
if (arr[i] > max)
max = arr[i];
}
int maxLength = (max + "").length();
for (int i = 0, n = 1; i < maxLength; i++, n *= 10) {
for (int j = 0; j < arr.length; j++) {
int digitElement = arr[j] / n % 10;
bucket[digitElement][bucketElementCounts[digitElement]] = arr[j];
bucketElementCounts[digitElement]++;
}
int index = 0;
for (int k = 0; k < bucketElementCounts.length; k++) {
if (bucketElementCounts[k] != 0){
for (int l = 0; l < bucketElementCounts[k]; l++) {
arr[index++] = bucket[k][l];
}
}
bucketElementCounts[k] = 0;
}
}
}
}