[数据结构与算法]插入排序算法

插入排序（Insertion Sort）一般也被称为直接插入排序。直接插入排序算法比较简单，容易实现，是一种稳定的排序算法。当待排序元素数量n很小且局部有序时，较为适用

它的基本思想是将一个关键字插入到已经排好序的有序列中，从而得到一个新的、元素数增1的有序列。假设在过程中，元素序列为 R[0…n-1]，首先将第一个元素 R[0] 看作一个有序子序列，然后依次将元素 R[i] (1<=i<=n-1)插入有序子序列 R[0…n-1] 中，使元素的有序子序列从 R[0…i-1] 变为 R[0…i]

实现要点

在其实现过程使用双层循环，外层循环对除了第一个元素之外的所有元素，内层循环对当前元素前面有序列进行待插入位置查找，并进行移动

测试用例： 使用插入排序算法将数组 { 4，2，8，0，5，7，1，3，6，9 } 进行升序排序

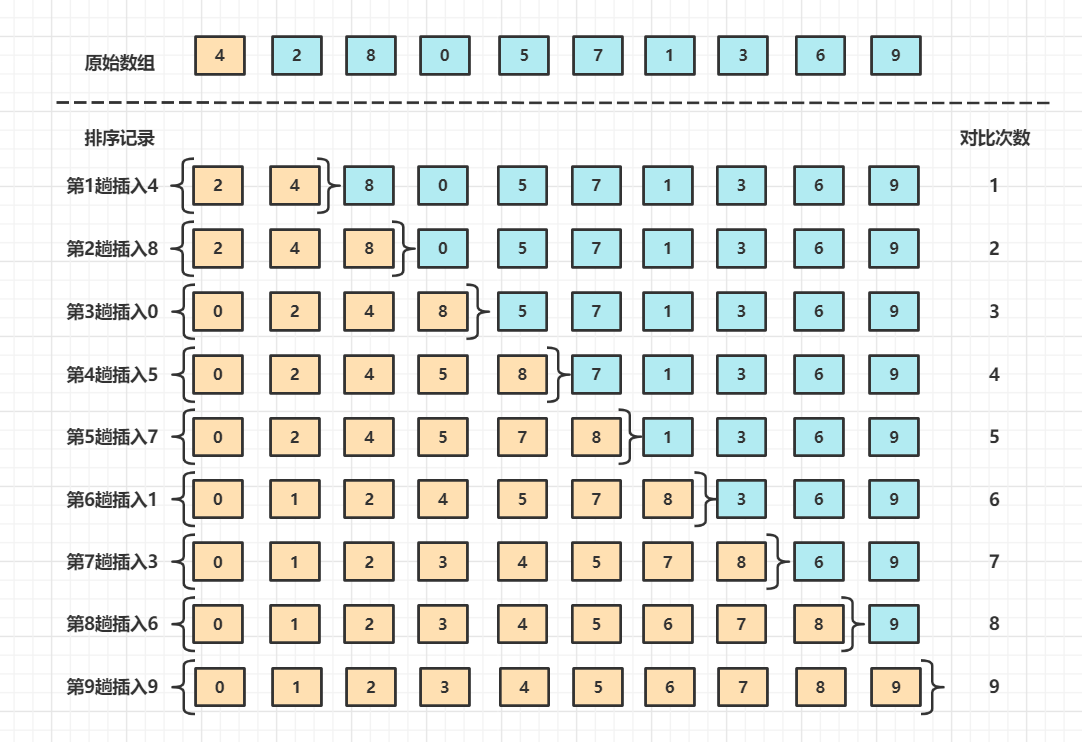
代码实现

package insertion_sorting;

public class InsertSorting {

    public static void main(String[] args) {
        InsertSorting insertSorting = new InsertSorting();
        int[] arr = new int[]{4,2,8,0,5,7,1,3,6,9};
        int[] afterSort = insertSorting.straightSort(arr, arr.length);
        long end = System.currentTimeMillis();


        System.out.print("排序之后的结果:{");
        StringBuffer buffer = new StringBuffer();
        for (int i = 0; i < afterSort.length; i++) {

            if (i != (afterSort.length-1)){
                buffer.append(afterSort[i]+",");
            } else buffer.append(afterSort[i]);
            
        }
        System.out.println(buffer.toString() + "}");
    }

    /**
     * 直接插入排序
     * 最好情况下的时间复杂度为O(n)
     * 最坏的情况下的时间复杂度和平均时间复杂度为O(n^2)
     * 在直接插入排序的过程中,需要一个元素大小的辅助空间用于存放待插入的元素,因此空间复杂度为O(1)
     * @param nums 数组
     * @param size 数组大小
     * @return 返回排列好的数组
     */
    public int[] straightSort(int[] nums, int size){
        int position, j;        // position为待插入的数据位置
        int temp;       // 用于存放待比较的值
        for (position = 1; position < size; position++) {   // 循环遍历数组
            temp = nums[position];      // 定义待比较的值
            for (j = position - 1; 0 <= j && temp < nums[j]; j--) {    // 循环遍历有序列,与temp比较值的大小,一直到数组下标0为止
                nums[j+1] = nums[j];    // 将大的元素向后移动,因为第j+1个元素本身就是temp,覆盖的话没有关系
                nums[j] = temp;         // 将小的替换大的元素的位置
            }
        }
        return nums;
    }
}

排序前：
4 2 8 0 5 7 1 3 6 9

排序后：
0 1 2 3 4 5 6 7 8 9

时间复杂度
最好的情况是，初始序列为有序，关键字总比较次数最小值为1 + 2 + 3 + . . . + (n-1)，也就是无须后移元素

最坏的情况是，初始序列为有序，关键字总比较次数为最大值1 + 2 + 3 + . . . + ( n ? 1 ) = n ( n ? 1 ) / 2 = $\frac{1}{2}{n}^2$ - $\frac{1}{2}n$ = $$\sum _{i=2}^{n}i$$
也就是每个关键字都需要与有序序列的每一个元素比较，时间复杂度为$O(n^2)$
上面那个例子就是最坏的情况下

空间复杂度
在直接插入排序的过程中，只需要一个元素大小的辅助空间用于存放待插入的元素，因此空间复杂度为$O(1)$