目录
一.全排列
1.题目
给定一个不含重复数字的数组?nums?,返回其?所有可能的全排列?。你可以?按任意顺序?返回答案。
示例:
输入:nums = [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
2思路图解
深度优先搜索的思想,创建一个flag数组来标记之前已经添加到list中的元素,如果当前元素已经添加过了,就跳过当前元素,继续向后找,找到一个未添加的元素,将该元素添加到list中,然后该位置的flag置为true, 之后以该位置开始再进行深度优先搜索,当以该元素为起点处理完成后,就需要进行回溯;首先将该位置的元素标记为flase,然后再从list中删除该元素。
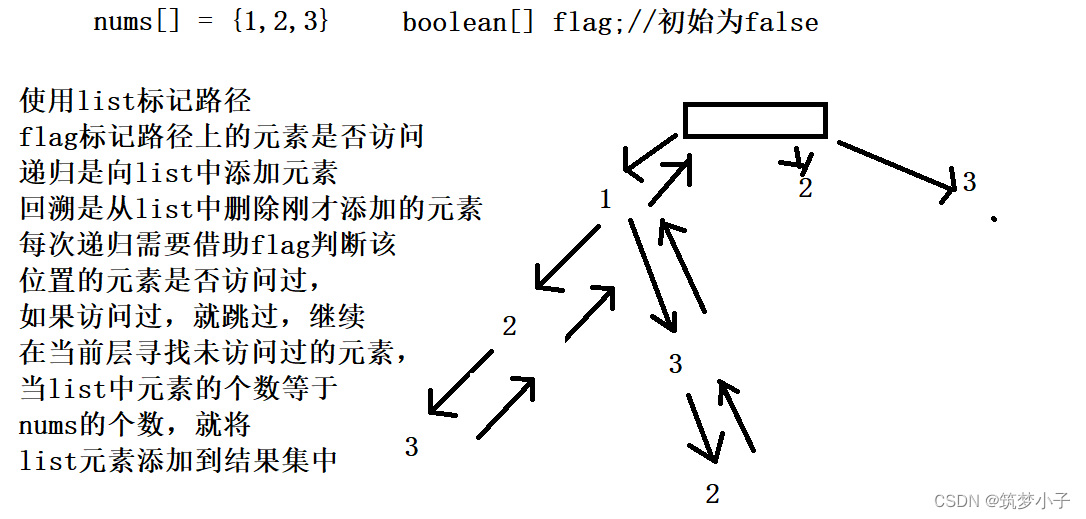
3.代码
List<List<Integer>> res = new ArrayList<>();
List<Integer> list = new ArrayList<>();
public List<List<Integer>> permute(int[] nums) {
//记录该位置的元素是否已经被访问
boolean[] flag = new boolean[nums.length];
dfs(nums, flag,0);
return res;
}
public void dfs(int[] nums, boolean[] flag, int count){
//说明所有元素已经排列
if(count == nums.length){
res.add(new ArrayList<>(list));
return;
}
for(int i=0; i<nums.length; i++) {
//当前位置的元素已经访问过,跳过
if(flag[i]) continue;
//没有访问,添加到结果集
list.add(nums[i]);
//标识当前位置的元素已经访问过
flag[i] = true;
dfs(nums, flag, count+1);
//在当前层继续向后进行寻找,修改当前位置元素未访问,然后在结果集中删除当前元素
flag[i] = false;
list.remove(list.size()-1);
}
}二.求最长连续序列(要求时间复杂度为O(N))
1.题目
给定一个未排序的整数数组 nums ,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。
请你设计并实现时间复杂度为?O(n) 的算法解决此问题。
示例:
输入:nums = [100,4,200,1,3,2]
输出:4
解释:最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。
2.思路图解
首先将所有元素存储在set集合中,将原数组元素去重,也是为了之后查找连续元素是否存在(查找的时间复杂度为O(1)),遍历原数组的所有元素,如果当前元素有前驱,就跳过(目的是为了从一个元素的开始位置查找比当前元素大的连续元素),在处理过程中保存长的连续结果集。

3.代码
public int longestConsecutive(int[] nums) {
Set<Integer> set = new HashSet<>();
for(int i=0; i<nums.length; i++) {
set.add(nums[i]);
}
int res = 0;
for(int i=0; i<nums.length; i++) {
//如果有前驱就跳过(为了从最开始的位置向后进行寻找)
if(!set.contains(nums[i]-1)) {
int count = 1;
int num = nums[i];
while(set.contains(++num)) {
count++;
}
res = Math.max(count, res);
}
}
return res;
}三.最长递增子序列
1.题目
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列?是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/longest-increasing-subsequence
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
示例:
输入:nums = [10,9,2,5,3,7,101,18] 输出:4 解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
2.思路图解
使用动态规划的思想,使用dp保存到当前位置的最长递增子序列;保存的思路是遍历当前位置前面所有的dp元素,如果当前元素比dp所在位置的元素大,那么就取当前位置的dp和前面比dp位置元素小的值+1,每找一个就和最终结果进行比较,并保存最终结果。

3.代码实现
public int lengthOfLIS(int[] nums) {
int[] dp = new int[nums.length];
int res = 0;
for(int i=0; i<nums.length; i++) {
dp[i] = 1;
for(int j=0; j<i; j++) {
if(nums[j]<nums[i])
dp[i] = Math.max(dp[i], dp[j]+1);
}
res = Math.max(dp[i], res);
}
return res;
}四.矩阵最长递增路径
1.题目
给定一个 n 行 m?列矩阵 matrix?,矩阵内所有数均为非负整数。 你需要在矩阵中找到一条最长路径,使这条路径上的元素是递增的。并输出这条最长路径的长度。
这个路径必须满足以下条件:
1. 对于每个单元格,你可以往上,下,左,右四个方向移动。 你不能在对角线方向上移动或移动到边界外。
2. 你不能走重复的单元格。即每个格子最多只能走一次。
示例:
输入:[[1,2,3],[4,5,6],[7,8,9]]
返回值:5
说明:1->2->3->6->9即可。当然这种递增路径不是唯一的。
2.思路图解
依次遍历每个元素并保存该元素的最长递增路径,采取的方式是保存一个当前元素递增路径的前一个元素;对于当前元素来说,寻找时,如果越界或比递增路径的前一个元素小,结束递归;如果比前一个元素大,就修改前一个元素为当前元素,然后依次去递归向上下左右进行寻找递增路径长度,使用一个max变量保存每个方向的最大递增路径长,之后对当前元素的递增路径+1,(满足递增要求)。

3.代码
public int solve (int[][] matrix) {
// write code here
int path =0;
for(int i=0; i<matrix.length; i++){
for(int j=0; j<matrix[0].length; j++) {
int tmp = dfs(matrix, i, j, -1);
//保存当前元素的最长递增路径长度
path = Math.max(path, tmp);
}
}
return path;
}
//使用pre保存之前的路径
public int dfs(int[][] ma, int i, int j , int pre){
//说明达到了边界或不符合递增规则
if(i<0 || j<0 || i>=ma.length || j>=ma[0].length || pre>=ma[i][j]) {
return 0;
}
pre = ma[i][j];
//保存当前路径的值和上下左右路径产生的最大值
int tmp = 0;
int max = 0;
//上
tmp = dfs(ma, i+1,j, pre);
max = Math.max(tmp, max);
//下
tmp = dfs(ma, i-1, j,pre);
max = Math.max(tmp, max);
//左
tmp = dfs(ma, i, j-1,pre);
max = Math.max(tmp, max);
//右
tmp = dfs(ma, i, j+1,pre);
max = Math.max(tmp, max);
//当前元素路径长加1
return max+1;
}五.旋转数组
1.题目
一个数组A中存有 n?个整数,在不允许使用另外数组的前提下,将每个整数循环向右移 M( M >=0)个位置,即将A中的数据由(A0?A1?……AN-1?)变换为(AN-M?…… AN-1?A0?A1?……AN-M-1?)(最后 M 个数循环移至最前面的 M 个位置)。如果需要考虑程序移动数据的次数尽量少,要如何设计移动的方法?
示例:
输入:6,2,[1,2,3,4,5,6]
返回值:[5,6,1,2,3,4]
2.思路图解

3.代码
public int[] solve (int n, int m, int[] a) {
// write code here
if(m==n) return a;
//去除掉n个元素的旋转
m=m%n;
//先反转所有,然后反转前m个,再反转剩余元素
reverse(a, 0, n-1);
reverse(a, 0, m-1);
reverse(a, m, n-1);
return a;
}
public void reverse(int[] a, int left, int right){
while(left<right) {
swap(a, left, right);
left++;
right--;
}
}
public void swap(int[] arr, int i , int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}六.最大数
1.题目
给定一组非负整数?nums,重新排列每个数的顺序(每个数不可拆分)使之组成一个最大的整数。
示例:
输入:nums = [10,2] 输出:"210"
2.思路图解
(1)先将整型数组转化为字符串数组
(2)按照字符串比较的结果大小进行降序排列
(3)然后将所有字符串拼接起来,防止全为0的情况,所以要去除多余的前导0
3.代码
public String largestNumber(int[] nums) {
int n = nums.length;
//先将整型数组转化为字符串数组
String[] strs = new String[n];
for(int i=0; i<n; i++) {
strs[i] = ""+nums[i];
}
//然后按照两个字符串拼接后结果的最大值进行排序
Arrays.sort(strs, (a, b)->{
return (b+a).compareTo(a+b);
});
//将结果拼接
StringBuilder sb = new StringBuilder();
for(int i=0; i<n; i++) {
sb.append(strs[i]);
}
//将前导多余的0去除掉
int k = 0;
while(k<sb.length()-1 && sb.charAt(k)=='0') k++;
return sb.substring(k);
}七.和为k的子数集
1.题目
给定一个整数数组和一个整数?k?,请找到该数组中和为?k?的连续子数组的个数。
输入:nums = [1,1,1], k = 2 输出: 2 解释: 此题 [1,1] 与 [1,1] 为两种不同的情况
2.思路图解
使用map集合,其中key为前i个元素之和,value为出现的sum和出现的次数;因为求的是连续子数组和为目标值,每次计算从0-i的元素和为sum,然后减去目标值sum-k,相当于0-j的元素和为sum-k,如果存在,那么就说明j-i的和等于k,最后统计所有连续和出现的次数。

3.代码
public int subarraySum(int[] nums, int k) {
Map<Integer, Integer> map = new HashMap<>();
map.put(0,1);
int sum = 0;
int count = 0;
for(int i=0; i<nums.length; i++) {
sum+=nums[i];
//每次查找0-j位置的元素是否满足
count += map.getOrDefault(sum-k, 0);
//将0-i的元素和插入
map.put(sum, map.getOrDefault(sum, 0)+1);
}
return count;
}八.划分为k个相等的子集
1.题目
给定一个整数数组??nums?和一个正整数?k,找出是否有可能把这个数组分成?k?个非空子集,其总和都相等。
输入: nums = [4, 3, 2, 3, 5, 2, 1], k = 4
输出: True
说明: 有可能将其分成 4 个子集(5),(1,4),(2,3),(2,3)等于总和。
2.思路图解
首先求数组元素和,然后判断是否可以整除k(判断是否可以分成k个子集),如果可以整除,然后就求出每个子集中元素的总和,再开始从数组中寻找子集和是否能够满足分割的要求,在寻找的过程中还需要借助一个数组来标记当前元素是否访问过,如果访问过,就跳过,之后如果k-1个子集都能满足要求,剩下的一个肯定可以满足(剪枝);由于时间复杂度比较高,还需要对数组进行排序,对于重复的元素进行跳过。

?
3.代码
public boolean canPartitionKSubsets(int[] nums, int k) {
int sum = 0;
for(int num:nums) sum+=num;
//判断是否可以分成k个区间
if(sum%k!=0) return false;
//求每个子集中元素和为多少
int target = sum/k;
//创建一个标志数组用来标记当前元素是否被访问过
boolean[] flag = new boolean[nums.length];
//对数组排序,方便之后剪枝
Arrays.sort(nums);
//如果最后一个元素比当前子集和大,就分割不成子集和
if(nums[nums.length-1]>target) return false;
return dfs(nums, nums.length-1, target, k, 0, flag);
}
/**
begin表示当前访问数组的开始位置,这里是从后向前访问
target 为所求集合中的目标值
sum 为当前集合的值
*/
public boolean dfs(int[] nums, int begin, int target, int k, int sum, boolean[] flag) {
//说明已经划分好区间,递归结束标志
if(k==1) return true;
//说明已经划分好一个区间了
if(target == sum) return dfs(nums, nums.length-1, target, k-1, 0, flag);
//开始从后向前循环寻找合适的子集和
for(int i=begin; i>=0; i--) {
//说明当前元素已经访问过
if(flag[i]) continue;
//说明当前元素不匹配,跳过
if(nums[i]+sum>target) continue;
//将当前元素加入到子集中继续递归向下寻找
flag[i] = true;
//说明向下寻找找到了当前元素开始作为子集和
if(dfs(nums, i-1, target, k, sum+nums[i], flag)) {
return true;
}
//回溯继续向后寻找
flag[i] = false;
//剪枝,如果前一个元素和当前元素相等,说明会重复处理,跳过
while(i>0 && nums[i-1]==nums[i]) i--;
}
//说明没有找到
return false;
}九.分割等和子集
1.题目
给你一个?只包含正整数?的?非空?数组?nums?。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
输入:nums = [1,5,11,5] 输出:true 解释:数组可以分割成 [1, 5, 5] 和 [11] 。
?
2.思路图解
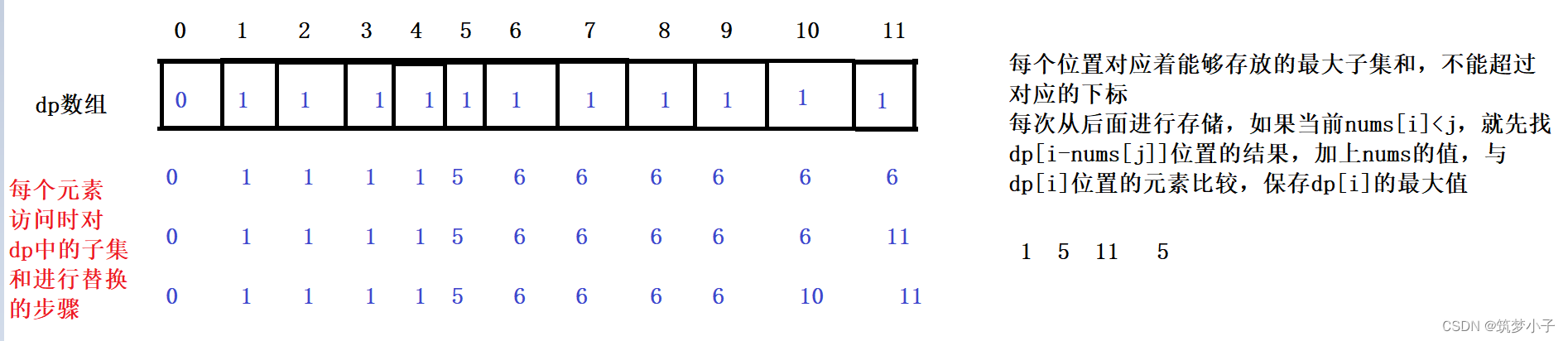
?
3.代码
public boolean canPartition(int[] nums) {
int sum = 0;
for(int num:nums) sum +=num;
//如果sum不能被2整除,说明不能分割成两个等和子集
if(sum%2!=0) return false;
//求子集中元素的和
int target = sum/2;
//使用dp数组,其中dp[i]的i=dp[i],对应着i元素的子集和大小
int[] dp = new int[target+1];
for(int i=0; i<nums.length; i++) {
//依次遍历每个元素,看是否可以添加到指定的子集和中
for(int j=target; j>=nums[i]; j--) {
//取背包所能容纳的最大值,进行保存
dp[j] = Math.max(dp[j], dp[j-nums[i]]+nums[i]);
}
}
return dp[target] == target;
}