文章目录
什么叫暴力递归:
1.把问题转化为规模缩小的同类问题的子问题
2.有明确的不需要继续进行递归的条件(base case)
3.有当得到了子问题的结果之后的决策过程
4.不记录每一个子问题的解
什么叫"尝试"
汉诺塔
打印n层汉诺塔从最左边移动到最右边的全部过程
方法:
主函数:调用:将n个盘子从左边到右边
只需要调用6个函数互相相互调用即可
- 左->右 右->左 左->中 中->左 右->中 中->右
#define _CRT_SECURE_NO_WARNINGS 1
#pragma once
#include<iostream>
using namespace std;
void leftToMid(int n);
void rightToMid(int n);
void rightToLeft(int n);
void midToLeft(int n);
void midToRight(int n);
void leftToRight(int n);
void leftToMid(int n)
{
if (n == 1)
{
printf("move 1 from left to mid\n");
return;
}
leftToRight(n-1);
printf("move %d from left to mid\n",n);
rightToMid(n - 1);
}
void rightToMid(int n)
{
if (n == 1)
{
printf("move 1 from right to mid\n");
return;
}
rightToLeft(n - 1);
printf("move %d from right to mid\n", n);
leftToMid(n - 1);
}
void rightToLeft(int n)
{
if (n == 1)
{
printf("move 1 from right to left\n");
return;
}
rightToMid(n - 1);
printf("move %d from right to left\n", n);
midToLeft(n - 1);
}
void midToLeft(int n)
{
if (n == 1)
{
printf("move 1 from mid to left\n");
return;
}
midToRight(n - 1);
printf("move %d from mid to left\n", n);
rightToLeft(n - 1);
}
void midToRight(int n)
{
if (n == 1)
{
printf("move 1 from mid to right\n");
return;
}
midToLeft(n - 1);
printf("move %d from mid to right\n", n);
leftToRight(n - 1);
}
void leftToRight(int n)//将n个盘子从左边移到右边
{
//方法:
//0.如果只有一个盘子,直接从左边移到右边
//1.把左边的n-1个盘子移到中间
//2.把左边的盘子移到右边
//3.把中间的n-1个盘子移到右边
if (n == 1)
{
printf("move 1 from left to right\n");
return;
}
leftToMid(n - 1);
printf("move %d from to right\n",n);
midToRight(n - 1);
}
//主函数:汉诺塔问题
void hanoi(int n)
{
leftToRight(n);//目标:把m个盘子从左边移到右边
}
int main()
{
hanoi(3);
return 0;
}
//输出结果:
move 1 from left to right
move 2 from left to mid
move 1 from right to mid
move 3 from to right
move 1 from mid to left
move 2 from mid to right
move 1 from left to right
不管是从哪里到哪里,其思想都是:

所以可以简写为:
void move(char from, char to)
{
printf("from %c to %c\n", from, to);
return;
}
/*
n:要移动的盘子数,
from:起始位置
other:中转位置
to:目的位置
*/
void process(int n, char from, char to, char other)
{
if (n == 1)
{
move(from, to);//只有一个盘子,直接从from移动到to
}
else
{
process(n - 1, from, other, to);//将from上的n-1个盘子经过to移动到other
move(from, to);//将第n个盘子从from移动到to
process(n - 1, other, to, from);//将other上的n-1个盘子经过from移动到to
}
}
void hanoi(int n)
{
if (n > 0)
process(n, 'A', 'C', 'B');//将A盘的n个盘子移到C盘
}
int main()
{
hanoi(3);
return 0;
}
//输出结果
from A to C
from A to B
from C to B
from A to C
from B to A
from B to C
from A to C
对于n层的汉诺塔,移动步数为2^n -1 步,所以时间复杂度:O(2^n -1)
打印一个字符串的全部子序列
//处理过程
//str固定参数,当前来到index位置,字符为str[index]
//str[0,index-1]已经走过了,之前的决定都记录在path
//str[index...]往后可以自由选择要不要,把所有生成的子序列放到ans中
void process(string str, int index, vector<string>& ans, string path)
{
//如果当前index来到字符串结尾,不能选择了,把之前做过的决定放到ans
if (index == str.size())
{
ans.push_back(path);
return;
}
//不要当前index位置的字符->path不变,往下递归
process(str, index + 1, ans, path);
//要当前index位置的字符->path加上当前字符,往下递归
process(str, index + 1, ans, path + str[index]);
}
//返回:s的所有子序列
vector<string> subs(string s)
{
string path = "";//记录当前形成的子序列
vector<string> v;
process(s, 0, v, path);
return v;
}
int main()
{
string s = "abc";
vector<string> ans = subs(s);
for (auto e : ans)
{
cout << e << " ";
}
return 0;
}
//输出结果:
c b bc a ac ab abc //第一个是空字符串
打印一个字符串的全部子序列,要求不要出现重复字面值的子序列
方法:只需在上一个题目的基础上用一个set容器去收集答案,进行去重即可
//处理过程
//str固定参数,当前来到index位置,字符为str[index]
//str[0,index-1]已经走过了,之前的决定都记录在path
//str[index...]往后可以自由选择要不要,把所有生成的子序列放到ans中
void process(string str, int index, unordered_set<string>& ans, string path)
{
//如果当前index来到字符串结尾,不能选择了,把之前做过的决定放到ans
if (index == str.size())
{
ans.insert(path);
return;
}
//不要当前index位置的字符->path不变,往下递归
process(str, index + 1, ans, path);
//要当前index位置的字符->path加上当前字符,往下递归
process(str, index + 1, ans, path + str[index]);
}
//返回:s的所有子序列(无重复)
vector<string> subs(string s)
{
string path = "";//记录当前形成的子序列
unordered_set<string> us;
process(s, 0, us, path);//用set去收集结果
vector<string> v;
for (auto& e : us)
{
v.push_back(e);
}
return v;
}
int main()
{
string s = "zzz";
vector<string> ans = subs(s);
for (auto e : ans)
{
cout << e << " ";
}
return 0;
}
//输出结果
zzz zz z
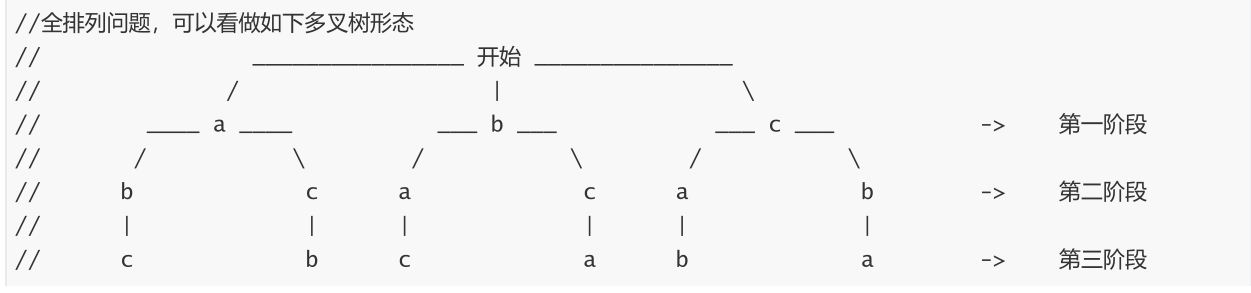
打印字符串的全部排列
全排列:所有的字符都要,只能决定顺序不一样!
第一部分:以哪个字符开头,第二部分:剩下的是子问题
所以,我们要让每个字符都要做一遍开头,然后在求解子问题
void process(string s, int index, vector<string>& ans)
{
if (index == s.size())
{
ans.push_back(s);
return;
}
else
{
//当前为index位置的字符
for (int i = index; i < s.size(); i++)
{
//index 和 i 的关系是:表示以谁开始
//每一步可以选择让谁做index位置的字符
//当确定以哪个字符作为开始,就要在决定另一部分的排列组合种类
swap(s[index], s[i]);
process(s, index + 1, ans);//递归处理下一个位置
swap(s[index], s[i]);//恢复现场
}
}
}
//打印字符串的全部排列
vector<string> permutation1(string s)
{
vector<string> ans;
if (s.size() == 0) return ans;
process(s,0,ans);
return ans;
}
int main()
{
vector<string> ans = permutation1("abc");
for (auto e : ans)
{
cout << e << " ";
}
return 0;
}
//输出结果:
abc acb bac bca cba cab
打印一个字符串的全部排列,要求不重复
https://leetcode.cn/problems/zi-fu-chuan-de-pai-lie-lcof/
如何实现去重?
方法1:先收集所有的全排列字符串,然后用set进行去重,这里是递归发生后检查
方法2:定义一个数组isExist来标志字符,这里实在递归发生分支之前就检查
class Solution {
public:
void process(string s,int index,vector<string>& ans)
{
if(index == s.size())
{
ans.push_back(s);
return ;
}
else
{
bool isExit[256] = {false};//去重
//当前为index位置
for(int i = index;i<s.size();i++)
{
//0位置的字符已经尝试过str[i]字符就不再尝试,否则进入判断
if(!isExit[s[i]])
{
isExit[s[i]]= true;
//每一步可以选择谁做index位置的字符
swap(s[index],s[i]);//让index位置的字符到i位置
process(s,index+1,ans);
swap(s[index],s[i]);//恢复现场
}
}
}
}
vector<string> permutation(string s) {
vector<string> ans ;
if(s.size() == 0)
return ans;
process(s,0,ans);
return ans;
}
};
方法3:对于全排列,STL有现成的函数next_permutation:
class Solution {
public:
vector<string> permutation(string s) {
sort(s.begin(), s.end());
vector<string> ans;
do ans.push_back(s);
while (next_permutation(s.begin(), s.end())); //全排列 + 排序
return ans;
}
};
不使用额外的数据结构,只能使用递归函数,逆序一个栈
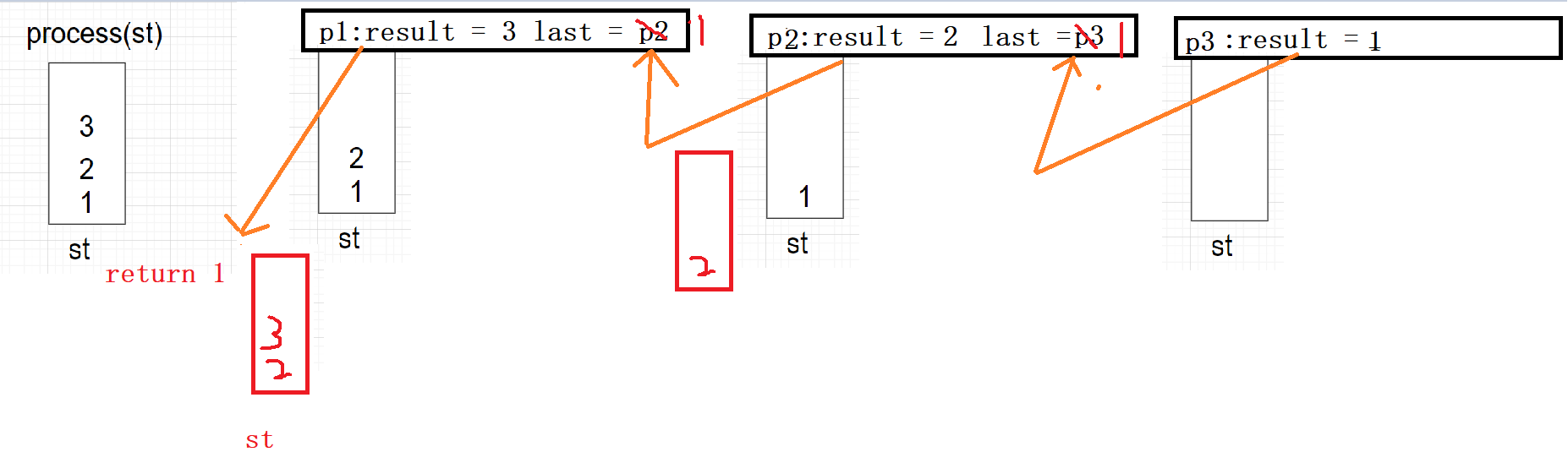
process函数图解:
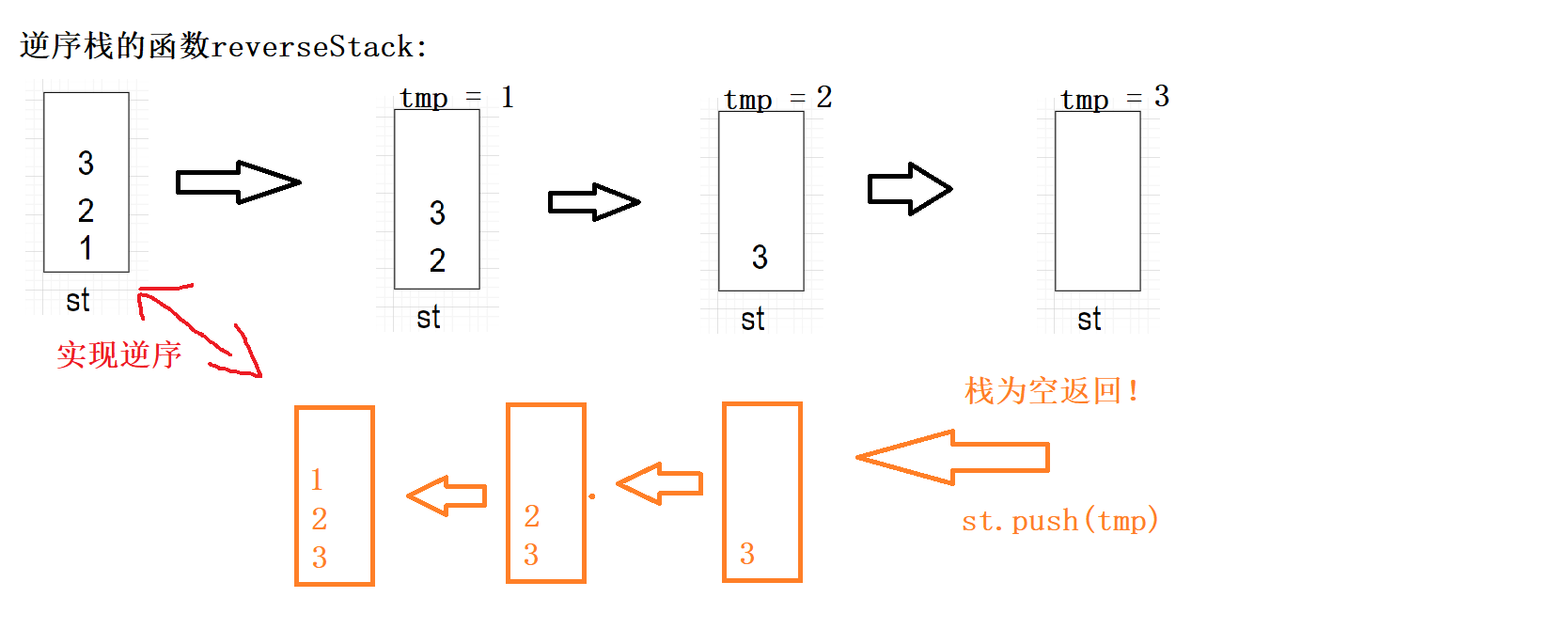
reverseStack函数图解
//process函数:移除栈顶元素并返回
int process(stack<int>& st)
{
int result = st.top();//栈顶元素
st.pop();
if (st.empty())
{
return result;
}
else
{
int last = process(st);
st.push(result);
return last;
}
}
void reverseStack(stack<int>& st)
{
if (st.empty())
{
return;
}
int tmp = process(st);
reverseStack(st);
st.push(tmp);
}
int main()
{
stack<int> st;
st.push(1);
st.push(2);
st.push(3);
reverseStack(st);
while (!st.empty())
{
cout << st.top() << endl; // 1 2 3
st.pop();
}
}