[数据结构与算法]常用的排序算法总结（持续更新...）

如何分析一个排序算法？

• 时间复杂度：决定了算法运行了多久
• 空间复杂度：执行算法的空间成本
• 比较次数&交换次数：排序会牵涉到的操作
• 稳定性：大小相同的两个值在排序之前和排序之后的先后顺序不变，这就是稳定的。反之则不稳定。

常用的排序算法

1、插入排序

插入排序算法的思路就是，往一个有序的集合中插入元素，插入后序列仍然有序。一个有序的数组，我们往里面添加一个新的数据后，如何继续保持数据有序呢？我们只要遍历数组，找到数据应该插入的位置将其插入即可。

具体步骤：

1. 将数组分成已排序段和未排序段。初始化时已排序段只有一个元素
2. 到未排序段取元素插入到已排序段，并保证插入后仍然有序
3. 重复执行上述操作，直到未排序段元素全部加完

例子：

对 5 2 6 3 9 1 进行插入排序（从小到大）

5 2 6 3 9 1

2 5 6 3 9 1

2 5 6 3 9 1

2 3 5 6 9 1

2 3 5 6 9 1

1 2 3 5 6 9

从以上操作中我们看到插入排序会经历一个元素的比较以及元素的移动。当我们从待排序列中取一个数插入到已排序区间时，需要拿它与已排序区间的数依次进行比较，注意，应从已排序区间的最后一个数开始往前比较，直到找到合适的位置，然后还要将插入点之后的元素进行往后移动。

代码实现：

public class InsertSort {
    public static void main(String[] args) {
        int data[] = {2, 5, 6, 3, 3, 9, 1, 10, 4, 23, 11};
        for (int i = 1; i < data.length; i++) {
            int j = i - 1;
            int temp = data[i];
            for (; j >= 0  ; j--) {
                if (temp < data[j]) {
                    data[j+1] = data[j];    // 数据往后移动
                } else {    // 前面已经排好序，那么找到一个比他小的就不用找了
                    break;
                }
            }
            data[j+1] = temp;
            System.out.println("第"+i+"次的排序结果为：");
            for (int k = 0; k < data.length; k++) {
                System.out.print(data[k]+" ");
            }
            System.out.println();
        }
    }
}

结论

• 时间复杂度：完全逆序极端情况下O(n^2)，完全有序最优情况下O(n)

• 空间复杂度：O(1)

• 稳定性：稳定

2、希尔排序

希尔排序其实是插入排序的改进版。

希尔排序是把记录按下标的一定增量分组，对每组使用插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。

具体步骤：

1. 先取一个整数i1=n/2(向下取整)作为第一个增量，把文件的全部记录分组。
2. 所有距离为i1的倍数的记录放在同一个组中。
3. 在各组内进行插入排序；
4. 取第二个增量i2=i1/2重复上述的分组和排序，直至所取的增量为1。

例子：

对 5 2 6 3 9 1 10 4 7 8 进行希尔排序（从小到大）

首先取第一个增量5=10/2
因此可分组为 [5,1][2,10][6,4][3,7][9,8]
分别插入排序后得 1 2 4 3 7 8 5 10 6 7 9

接着取第二个增量2=5/2
因此可分组为==[5,6,9,10,7][2,3,1,4,8]==
分别插入排序后的 5 1 6 2 7 3 9 4 10 8

最后取增量为1
直接进行插入排序得 1 2 3 4 5 6 7 8 9 10

从以上操作可知，希尔排序其实就是分成很多小组使序列尽可能的变成有序段。因为我们通过对插入排序分析可知，插入排序对已经排好序的序列速度是很快的。

代码实现：

public class HillSort {
    public static void main(String[] args) {
        int arr[] = {5, 2, 6, 3, 9, 1, 10, 4, 7, 8};
        for (int gap = arr.length / 2; gap > 0; gap /= 2) {
            for (int i = gap; i < arr.length; i++) {
                int curr = arr[i];
                int prev = i - gap;
                while (prev >= 0 && curr < arr[prev]) {
                    arr[prev + gap] = arr[prev];
                    prev -= gap;
                }
                arr[prev + gap] = curr;
            }
            System.out.println(Arrays.toString(arr));
        }
    }
}

结论：

• 时间复杂度：O(n^(1.3-2))
• 空间复杂度：O(1)
• 稳定性：稳定

3、归并排序

归并排序是一种非常高效的排序算法，其核心思想就用到了递归和分治的思想。

具体步骤：

1. 把数组从中间分为两个子数组
2. 递归把子数组从中间分为更小的子数组，直至子数组只有一个元素
3. 依次按照递归的返回顺序，不断地合并排好序的子数组，直到最后把整个数组的顺序排好。

例子：

合并是如何排序的？

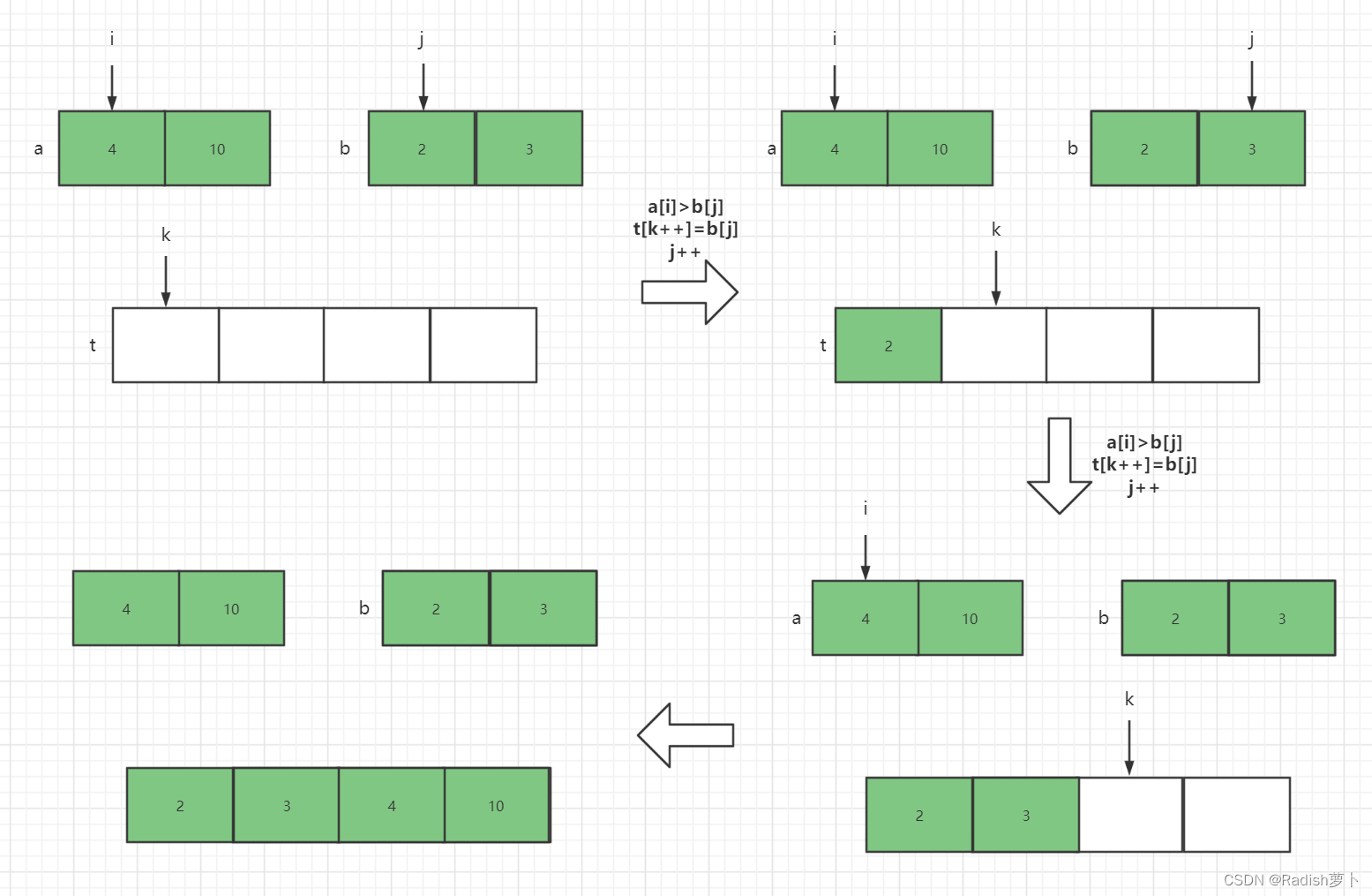
代码实现：

public class MergeSort {
    public static void main(String[] args) {
        int arr[] = {10, 4, 2, 3, 8, 1, 6, 7};
        separate(arr, 0, arr.length - 1);
        System.out.println(Arrays.toString(arr));
    }

    /**
     * 拆开
     * @param arr
     */
    public static void separate(int arr[], int left, int right) {
        if (left < right) { // 相等了就表示只有一个数了 不用再拆了
            int mid = (left + right) / 2; // 3 1 0
            separate(arr, left, mid);
            separate(arr, mid + 1, right);
            // 进行合并
            merge(arr, left, mid, right);
        }
    }

    private static void merge(int[] arr, int left, int mid, int right) {
        int temp[] = new int[arr.length];   // 临时变量用来保存合并的数据

        int point1 = left;		// 左边的第一个数的位置
        int point2 = mid + 1;	// 右边的第一个数的位置

        int loc = left;		// 当前位置
        while(point1 <= mid && point2 <= right){
            if(arr[point1] < arr[point2]){
                temp[loc] = arr[point1];
                point1++ ;
                loc++ ;
            }else{
                temp[loc] = arr[point2];
                point2++;
                loc++ ;
            }
        }
        // 把剩余部分补上
        while(point1 <= mid){
            temp[loc++] = arr[point1++];
        }
        while(point2 <= right){
            temp[loc++] = arr[point2++];
        }
        // 赋值回原数组
        for(int i = left ; i <= right ; i++){
            arr[i] = temp[i];
        }
    }
}

结论：

• 时间复杂度：O(nlogn)
• 空间复杂度：O(n)
• 稳定性：稳定

4、选择排序

选择排序和插入排序的思路相似，也分已排序和未排序区间。但选择排序每次会从未排序区间中找到最小的元素，将其放到已排序区间的末尾。但是不像插入排序会移动数组 选择排序会每次进行交换。

例子：

对 5 2 6 3 9 1 进行选择排序（从小到大）

5 2 6 3 9 1

1 2 6 3 9 5

1 2 6 3 9 5

1 2 3 6 9 5

1 2 3 5 9 6

1 2 3 5 6 9

代码实现：

public class SelectSort {
    public static void main(String[] args) {
        int arr[] = {5, 2, 6, 3, 9, 1};
        int temp;
        for (int i = 0; i < arr.length - 1 ; i++) {
            for (int j = i; j < arr.length; j++) {
                if (arr[i] > arr[j]) {
                    temp = arr[i];
                    arr[i] = arr[j];
                    arr[j] = temp;
                }
            }
        }
        System.out.println(Arrays.toString(arr));
    }
}

总结：

• 时间复杂度：O(n^2)
• 空间复杂度：O(1)
• 稳定性：不稳定

5、冒泡排序

冒泡排序只会操作相邻的两个数据。每次冒泡操作都会对相邻的两个元素进行比较，看是否满足大小关系要求。如果不满足就让它俩互换。一次冒泡会让至少一个元素移动到它应该在的位置，重复n次，就完成了n个数据的排序工作。

例子：

对 5 2 6 3 9 1 进行选择排序（从小到大）

第一次冒泡结果：5 2 6 3 9 1 -> 2 5 6 3 9 1 -> 2 5 6 3 9 1 -> 2 5 3 6 9 1 -> 2 5 3 6 9 1 -> 2 5 3 6 1 9

第二次冒泡结果：2 5 3 6 1 9 -> 2 3 5 6 1 9 -> 2 3 5 6 1 9 -> 2 3 5 1 6 9 -> 2 3 5 1 6 9

第三次冒泡结果：2 3 5 1 6 9 -> 2 3 5 1 6 9 -> 2 3 5 1 6 9 -> 2 3 1 5 6 9

第四次冒泡结果：2 3 1 5 6 9 -> 2 3 1 5 6 9 -> 2 1 3 5 6 9

第五次冒泡结果：2 1 3 5 6 9 -> 1 2 3 5 6 9

代码实现：

public class BubbleSort {
    public static void main(String[] args) {
        int arr[] = {5, 2, 6, 3, 9, 1};
        int temp;
        for (int i = 0; i < arr.length - 1; i++) {
            boolean flag = false;
            for (int j = 0; j < arr.length - i - 1; j++) {
                if (arr[j] > arr[j+1]) {
                    temp = arr[j];
                    arr[j] = arr[j+1];
                    arr[j+1] = temp;
                    flag = true;
                }
            }
            if (!flag) {
                break;
            }
        }
        System.out.println(Arrays.toString(arr));
    }
}

总结：

• 时间复杂度：最坏情况下O(n^2)，最好情况下O(n)
• 空间复杂度：O(1)
• 稳定性：稳定

6、快速排序

快速排序是一个既高效又不浪费空间的一种排序算法。

步骤与例子：

对 5 2 6 3 9 1 10 4 7 8 进行快速排序（从小到大）

首先选取第一个数5作为基准数

从后面往前找到比基准数小的数进行对换：

4 2 6 3 9 1 10 5 7 8

从前面往后面找比基准数大的进行对换：

4 2 5 3 9 1 10 6 7 8

从后面往前找到比基准数小的数进行对换：

4 2 1 3 9 5 10 6 7 8

从前面往后面找比基准数大的进行对换：

4 2 1 3 5 9 10 6 7 8

最后得到比基准数小的都在其左边，比基准数大的都在其右边 {4 2 1 3} 5 {9 10 6 7 8}

到此第一次以5为基准数的排序完成。

之后分别对{4 2 1 3}，{9 10 6 7 8}重复上述操作

public class QuickSort {
    public static void main(String[] args) {
        int arr[] = {5, 2, 6, 3, 9, 1, 10, 4, 7, 8};
        quick(arr, 0, arr.length - 1);
        System.out.println(Arrays.toString(arr));
    }

    public static void quick(int arr[], int left, int right) {
        int base = arr[left];   // 基准数
        int ll = left;          // 从左边开始找的位置
        int rr = right;         // 从右边开始找的位置
        while (ll < rr) {
            // 从后面往前找比基准数小的数
            while (ll < rr && arr[rr] >= base) {
                rr--;
            }
            if (ll < rr) {
                arr[ll] = arr[rr];
                arr[rr] = base;
                ll++;
            }
            // 从前面往后找比基准数小的数
            while (ll < rr && arr[ll] <= base) {
                ll++;
            }
            if (ll < rr) {
                arr[rr] = arr[ll];
                arr[ll] = base;
                rr--;
            }
        }
        if (left < ll) {
            quick(arr, left, ll - 1);
        }
        if (ll < right) {
            quick(arr, ll + 1, right);
        }

    }
}