题目

题目连接

给你两个下标从 0 开始的整数数组 nums1 和 nums2 ，长度为 n 。
数组 nums1 和 nums2 的差值平方和定义为所有满足 0 <= i < n 的 (nums1[i] - nums2[i])2 之和。
同时给你两个正整数 k1 和 k2 。你可以将 nums1 中的任意元素 +1 或者 -1 至多 k1 次。类似的，你可以将 nums2 中的任意元素 +1 或者 -1 至多 k2 次。

请你返回修改数组 nums1 至多 k1 次且修改数组 nums2 至多 k2 次后的最小差值平方和。
注意：你可以将数组中的元素变成负整数。

示例 1：

输入：nums1 = [1,2,3,4], nums2 = [2,10,20,19], k1 = 0, k2 = 0
输出：579
解释：nums1 和 nums2 中的元素不能修改，因为 k1 = 0 和 k2 = 0 。
差值平方和为：(1 - 2)2 + (2 - 10)2 + (3 - 20)2 + (4 - 19)2 = 579 。

示例 2：

输入：nums1 = [1,4,10,12], nums2 = [5,8,6,9], k1 = 1, k2 = 1
输出：43
解释：一种得到最小差值平方和的方式为：
- 将 nums1[0] 增加一次。
- 将 nums2[2] 增加一次。
最小差值平方和为：
(2 - 5)2 + (4 - 8)2 + (10 - 7)2 + (12 - 9)2 = 43 。
注意，也有其他方式可以得到最小差值平方和，但没有得到比 43 更小答案的方案。

解题

方法一：贪心+优先队列（超时）

首先计算两个数组的差diff，为了使得平方和最小，也就是说差要小点。
k1和k2可以合起来一起考虑的(k=k1+k2)，因为只要使得diff中的元素小就行了。

比如diff=[3,4]，k=1
显然 $3^2+(4-1)^2$ 比 $3-1)^2+4^2$ 来的小
因此，
贪心的思路：使得大的数先变小。这样总和才能最小。

实现方法：

把所有数放入大顶堆中，
把最大的数-1，然后再放回去。重复最多k次
最后把大顶堆中所有的结果求平方和

class Solution {
public:
    long long minSumSquareDiff(vector<int>& nums1, vector<int>& nums2, int k1, int k2) {
        int n=nums1.size();
        int k=k1+k2;
        priority_queue<int,vector<int>,less<int>> q;
        for(int i=0;i<n;i++){
            q.push(abs(nums1[i]-nums2[i]));
        }
        
        while(k--){
            int tmp=q.top();
            if(tmp==0) break;
            q.pop();
            q.push(--tmp);
        }
        long long res=0;
        while(!q.empty()){
            int tmp=q.top();
            q.pop();
            res+=(long long)tmp*tmp;
        }
        return res;
        
        
    }
};

复杂度为O(n)，可是依旧超时了。可能是因为优先队列频繁push和pop导致的，因为k的值比较大。

方法二：贪心+数组

由于大顶堆存在超时，那么如果同样的思路，用数组实现呢？

diff[i]:表示差值为i的数量有diff[i]个

从diff末尾开始遍历，先处理大的数，让它们的值-1，数量为diff[i]
值从i变成i-1，变化的数量为diff[i]

class Solution {
public:
    long long minSumSquareDiff(vector<int>& nums1, vector<int>& nums2, int k1, int k2) {
        int n=nums1.size(),k=k1+k2;
        vector<int> diff(1e5+1,0);
        for(int i=0;i<n;i++) diff[abs(nums1[i]-nums2[i])]++;

        for(int i=diff.size()-1;i>0&&k>0;i--){
            int change=min(k,diff[i]);
            diff[i-1]+=change;
            k-=change;
            diff[i]-=change;
        }
        
        long long res=0;
        for(int i=0;i<diff.size();i++){
            res+=pow(i,2)*diff[i];
        }
        return res;

    }
};

方法三：贪心+二分查找

贪心思想：使得大的数先变小
进一步思考：比如有diff=[10,12,3]，k=5
减去2次后，变成[10,10,3],k=3，那么接下去就是两个10轮流减少了，因为两个都是最大。
那么就可以想象一条线，把他们截断

二分查找思路：
绿色的部分就是减去的值s。

如果s>k,说明减去太多了，截断的线应该向上，mid+1
如果s<=k,说明减去太少了，截断线应该向下

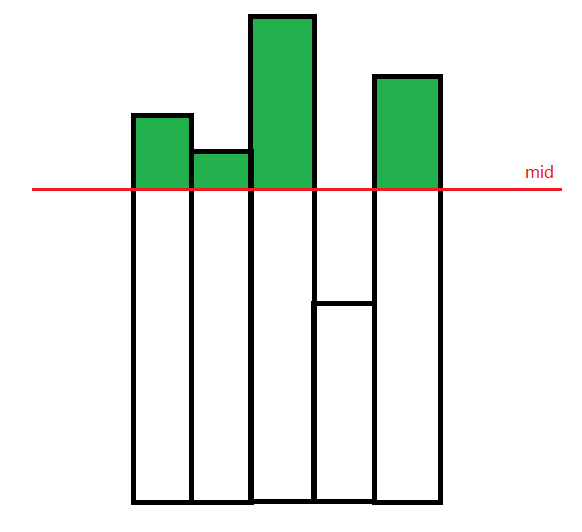
在这里插入图片描述
这种截断线的好处是，可以批量截断，运行速率快。如上图中，每向下移动，多减去4次，万一s+4比k多了呢？因此要使得s尽可能大，但不超过k。剩下次数为count，最后再计算。

最后一种情况是，截断线可以是0处，说明k的大小很大，可以把所有平方和置为0。因此如果截断线是0的话，平方和就是0。

class Solution {
public:
    long long minSumSquareDiff(vector<int>& nums1, vector<int>& nums2, int k1, int k2) {
        int n=nums1.size(),k=k1+k2,left=0,right=10000000,count=0;
        vector<int> diff(n);
        for(int i=0;i<n;i++){
            diff[i]=abs(nums1[i]-nums2[i]);
        }

        while(left<right){
            int mid=(left+right)/2;
            long s=0;
            for(int num:diff){
                s+=max(0,num-mid);
            }
            if(s>k) left=mid+1;
            else{
                right=mid;
                count=k-s;
            }
        }
        long res=0;
        for(int num:diff){
            res+=pow(num<left?num:left-min(1,max(0,count--)),2);
        }
        return left>0?res:0;

    }
};