1.题目

?2.思路

2.1穷举法（不推荐）

时间复杂度O(n^2)

思路如下：

双层遍历，枚举每一个元素去与数组中的其他元素比较

判断是否等于target，如果有，返回下标即可

2.2哈希映射（推荐）

时间复杂度O(n)

我们发现上一种方法的时间复杂度与空间复杂度比较大，所以我们使用哈希表来

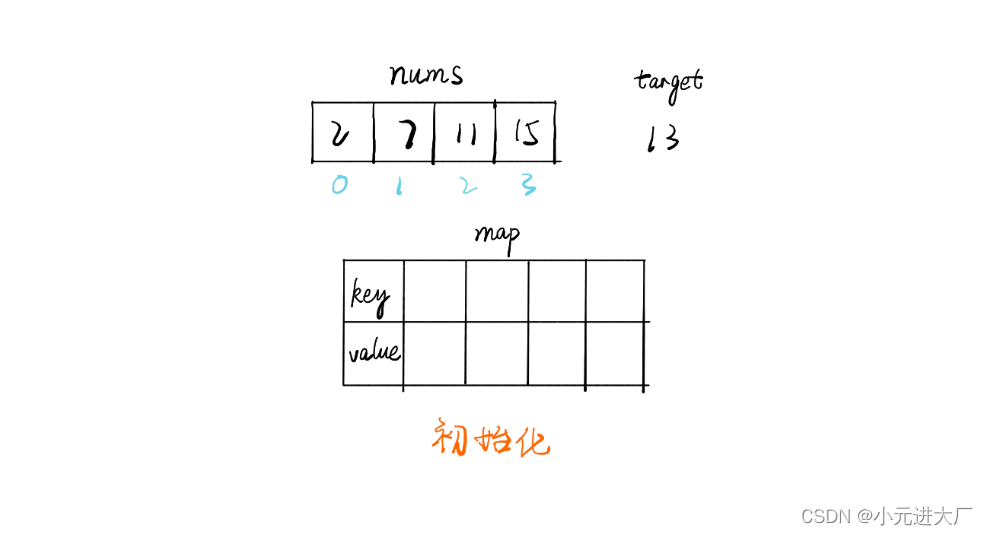
思路如下：

遍历数组
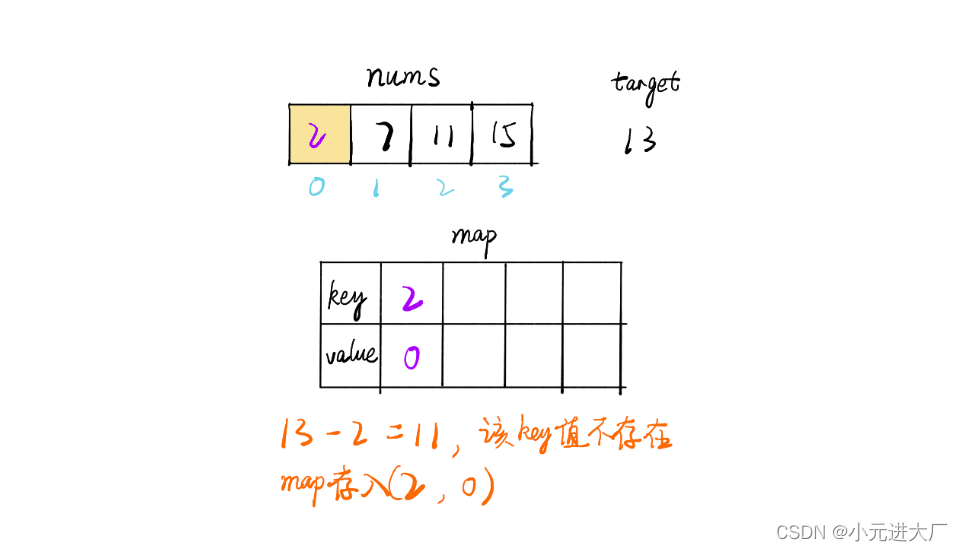
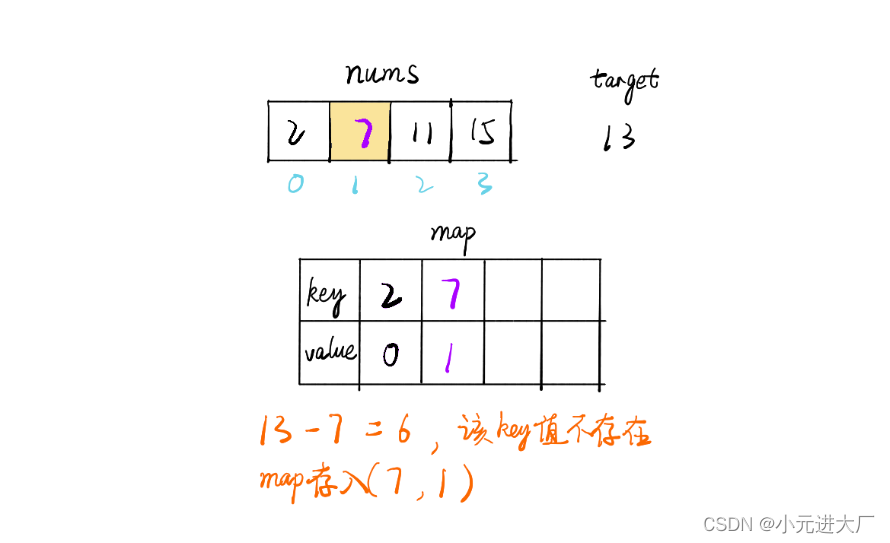
判断在哈希表中是否存在? ?target-nums[i]? ?这个元素
如果存在，返回元素的下标即可
如果不存在，将此时的nums[i]存入哈希表中，然后继续遍历
遍历完整个数组，说明不存在，返回null即可

图解（搬自画手大鹏，如有侵权可以删除）如下：?

3.代码实现

3.1穷举

class Solution {
    public int[] twoSum(int[] nums, int target) {
        int index1 = -1;
        int index2 = -1;
        for(int i = 0; i<nums.length ;i++) {
            for(int j = i+1; j<nums.length ;j++) {
                if(nums[i]+nums[j] == target) {
                    index1 = i;
                    index2 = j;
                }
            }
        }
        if(index1>=0 && index2>=0) {
            int[] num = {index1,index2};
            return num;
        }
        return null;
        
    }
}

3.2哈希表

class Solution {
    public int[] twoSum(int[] nums, int target) {

        Map <Integer,Integer>m1 = new HashMap<>();
        for(int i = 0; i < nums.length ; i++) {
            if(m1.containsKey(target - nums[i])) {
                return new int[] {m1.get(target-nums[i]),i};
            }
            m1.put(nums[i],i);
        }
        return null;
    }
}