目录
912. 排序数组
一、归并排序
归并排序的过程可以在逻辑上抽象成一棵二叉树,树上的每个节点的值是?nums[lo..hi],叶子节点的值就是数组中的单个元素,排序过程如下图所示(来源:labuladong)。
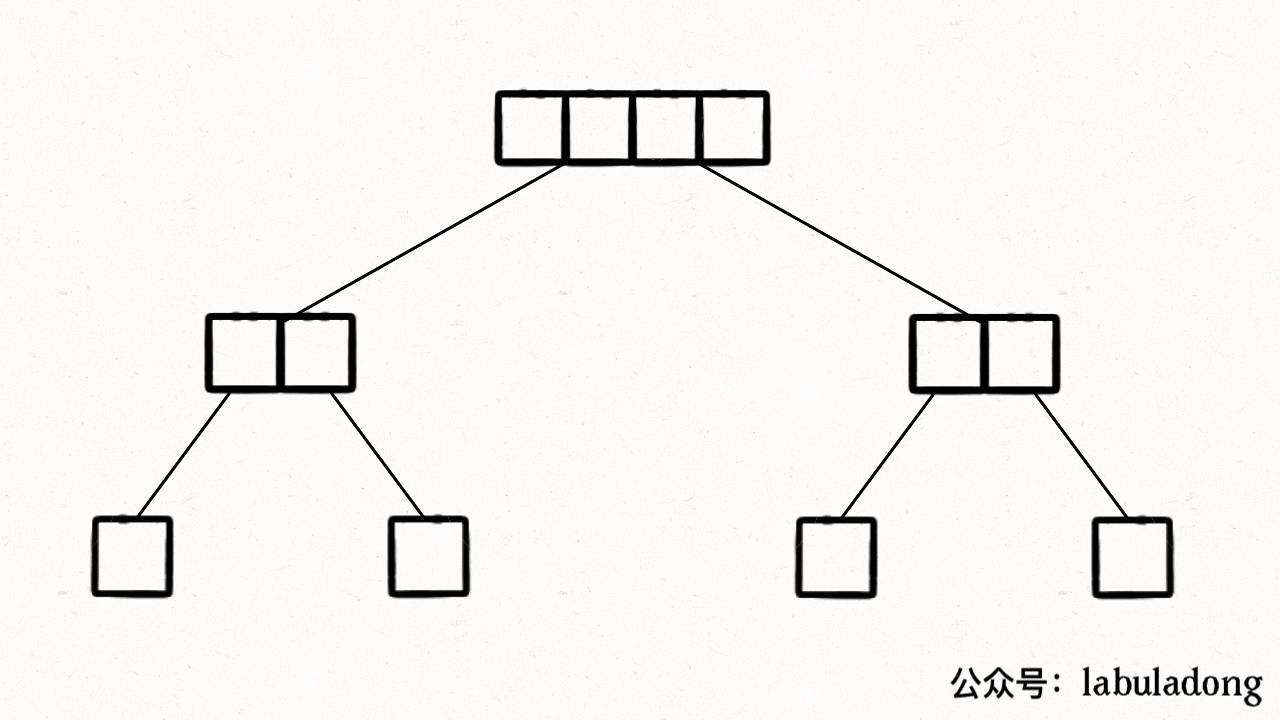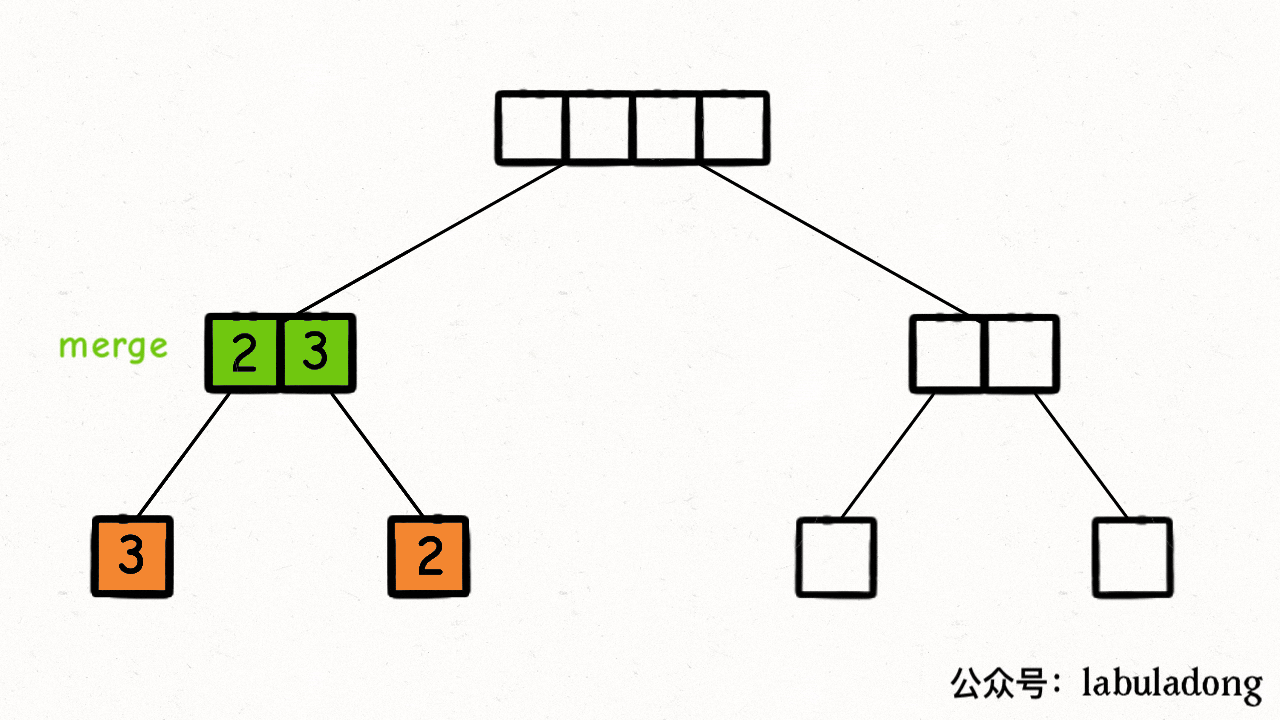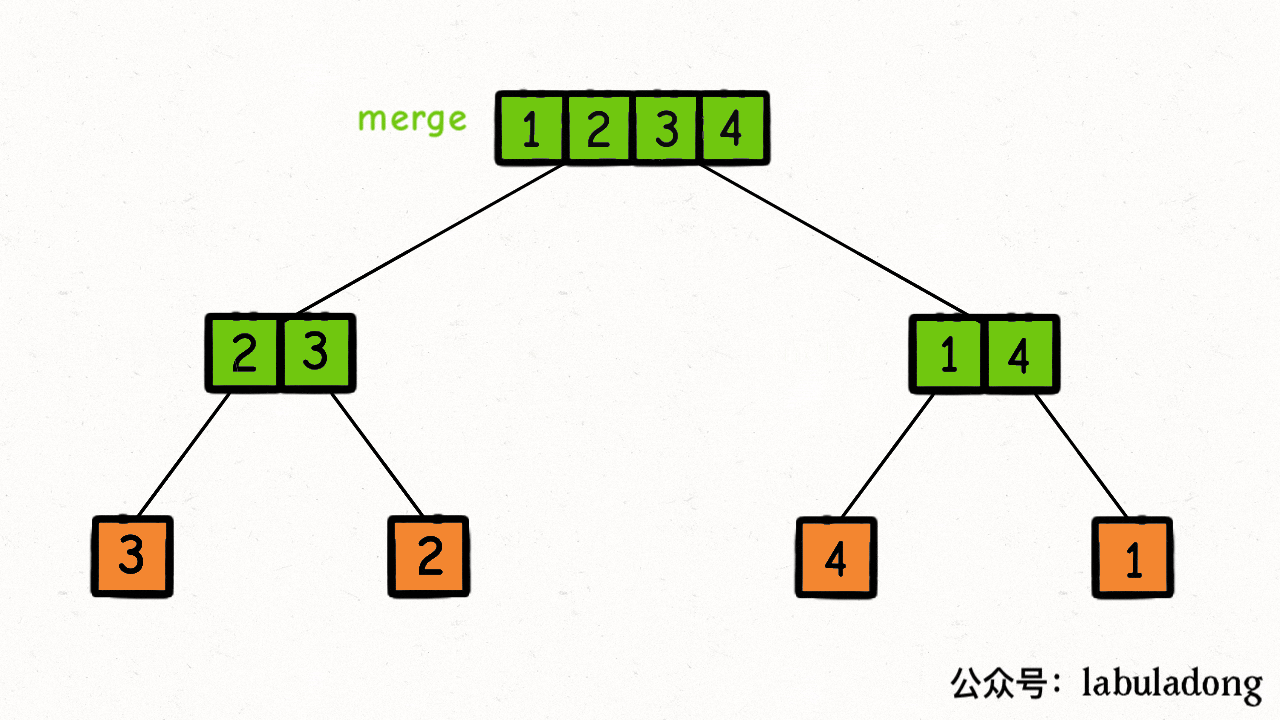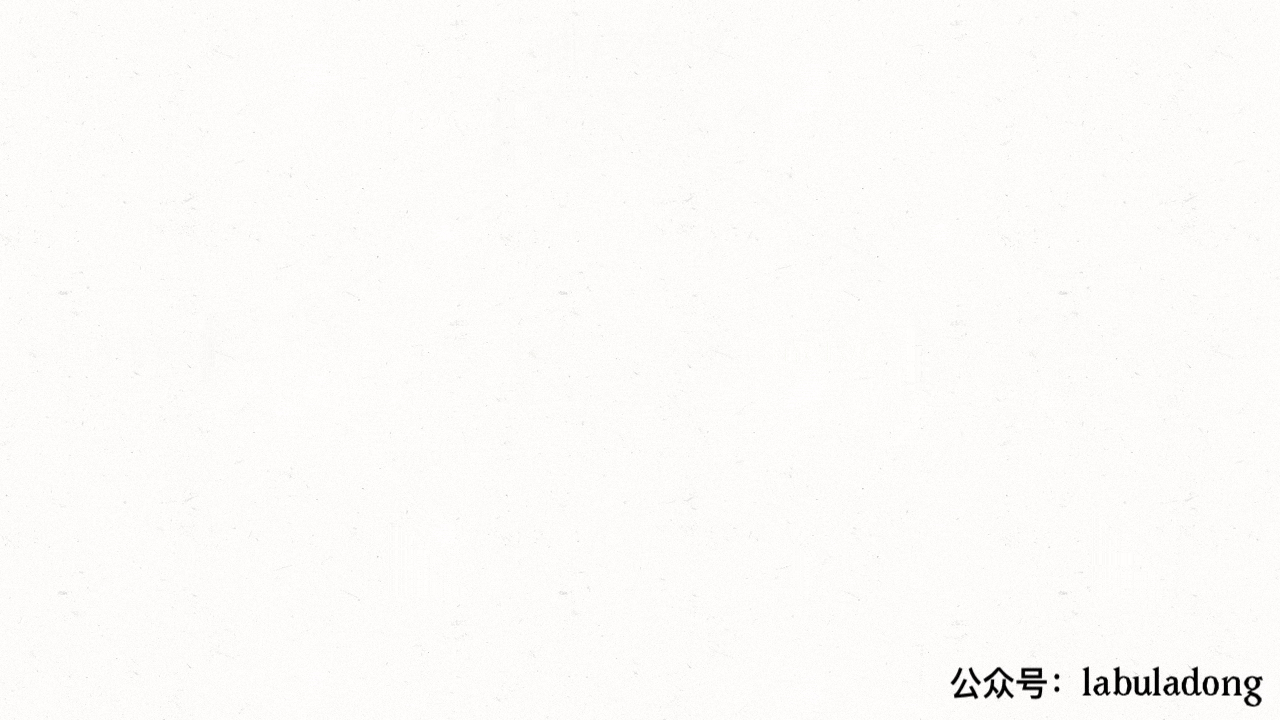
merge?操作会在二叉树的每个节点上都执行一遍,执行顺序是二叉树后序遍历的顺序。?
class Solution {
public:
vector<int> sortArray(vector<int>& nums) {
temp.resize(nums.size());
Sort(nums, 0, nums.size() - 1);
return nums;
}
private:
// 初始化一个辅助数组,避免递归时内存频繁分配释放
vector<int> temp;
void Sort(vector<int>& nums, int left, int right) {
// 只剩下一个元素,无需继续排序
if (left == right) {
return;
}
int mid = left + (right - left) / 2;
// 排序左侧数组[left, mid]
Sort(nums, left, mid);
// 排序右侧数组[mid + 1, right]
Sort(nums, mid + 1, right);
// 将有序的左右数组按顺序合并
Merge(nums, left, mid, right);
}
void Merge(vector<int>& nums, int left, int mid, int right) {
// 把 nums[left, right] 复制到辅助数组中,以便合并后的结果能够直接存入 nums
for (size_t i = left; i <= right; ++i) temp[i] = nums[i];
// 利用双指针技巧,合并两个有序数组
int left_p = left, right_p = mid + 1;
for (size_t p = left; p <= right; ++p) {
// 左侧数组已经merge完毕,只需要移动右侧数组的指针
if (left_p == mid + 1) nums[p] = temp[right_p++];
// 右侧数组已经merge完毕,只需要移动左侧数组的指针
else if (right_p == right + 1) nums[p] = temp[left_p++];
// 升序:左侧数比右侧数小,加入左侧元素
else if (temp[left_p] < temp[right_p]) nums[p] = temp[left_p++];
// 升序:右侧数比左侧数小,加入右侧元素
else nums[p] = temp[right_p++];
}
}
};归并排序的技巧在于:不是在?merge?函数执行的时候 new 辅助数组,而是提前把?temp?辅助数组 new 出来了,这样就避免了在递归中频繁分配和释放内存可能产生的性能问题。
?时间复杂度:O(NlogN)
对于归并排序来说,时间复杂度集中在?
merge?函数遍历?nums[left,right]?的过程。Merge执行的次数是二叉树节点的个数,每次执行的复杂度就是每个节点代表的子数组的长度,所以总的时间复杂度就是整棵树中「数组元素」的个数。从整体上看,二叉树的高度是?
logN,其中每一层的元素个数就是原数组的长度?N,所以总的时间复杂度就是?O(NlogN)。【logN层,每层N次】
?315. 计算右侧小于当前元素的个数[*]
class Solution {
typedef pair<int, int> Vidx;
public:
vector<int> countSmaller(vector<int>& nums) {
// 初始化数组,使之成为键值对,携带下标信息
vector<Vidx> arr;
for (int i = 0; i < nums.size(); ++i) {
arr.push_back(make_pair(nums[i], i));
}
temp.resize(nums.size());
count.resize(nums.size());
Sort(arr, 0, arr.size() - 1);
return count;
}
private:
// 记录右侧小于 nums[i] 的元素的数量
vector<int> count;
// 初始化一个辅助数组,避免递归时内存频繁分配释放;同时还要记录下标位置
vector<Vidx> temp;
void Sort(vector<Vidx>& arr, int left, int right) {
// 只剩下一个元素,无需继续排序
if (left == right) {
return;
}
int mid = left + (right - left) / 2;
// 排序左侧数组[left, mid]
Sort(arr, left, mid);
// 排序右侧数组[mid + 1, right]
Sort(arr, mid + 1, right);
// 将有序的左右数组按顺序合并
Merge(arr, left, mid, right);
}
void Merge(vector<Vidx>& arr, int left, int mid, int right) {
// 把 nums[left, right] 复制到辅助数组中,以便合并后的结果能够直接存入 nums
for (size_t i = left; i <= right; ++i) temp[i] = arr[i];
// 利用双指针技巧,合并两个有序数组
int left_p = left, right_p = mid + 1;
for (size_t p = left; p <= right; ++p) {
// 左侧数组已经merge完毕,只需要移动右侧数组的指针
if (left_p == mid + 1) arr[p] = temp[right_p++];
// 右侧数组已经merge完毕,只需要移动左侧数组的指针
else if (right_p == right + 1) {
arr[p] = temp[left_p++];
// 更新 count 数组
count[arr[p].second] += right_p - mid - 1;
}
// 升序:左侧数比右侧数小,加入左侧元素
else if (temp[left_p].first <= temp[right_p].first) {
arr[p] = temp[left_p++];
// 更新 count 数组
count[arr[p].second] += right_p - mid - 1;
}
// 升序:右侧数比右侧数小,加入右侧元素
else arr[p] = temp[right_p++];
}
}
};在使用?merge?函数合并两个有序数组的时候,其实是可以知道一个元素?nums[i]?后边有多少个元素比?nums[i]?小的。如下图所示(来源:labuladong):
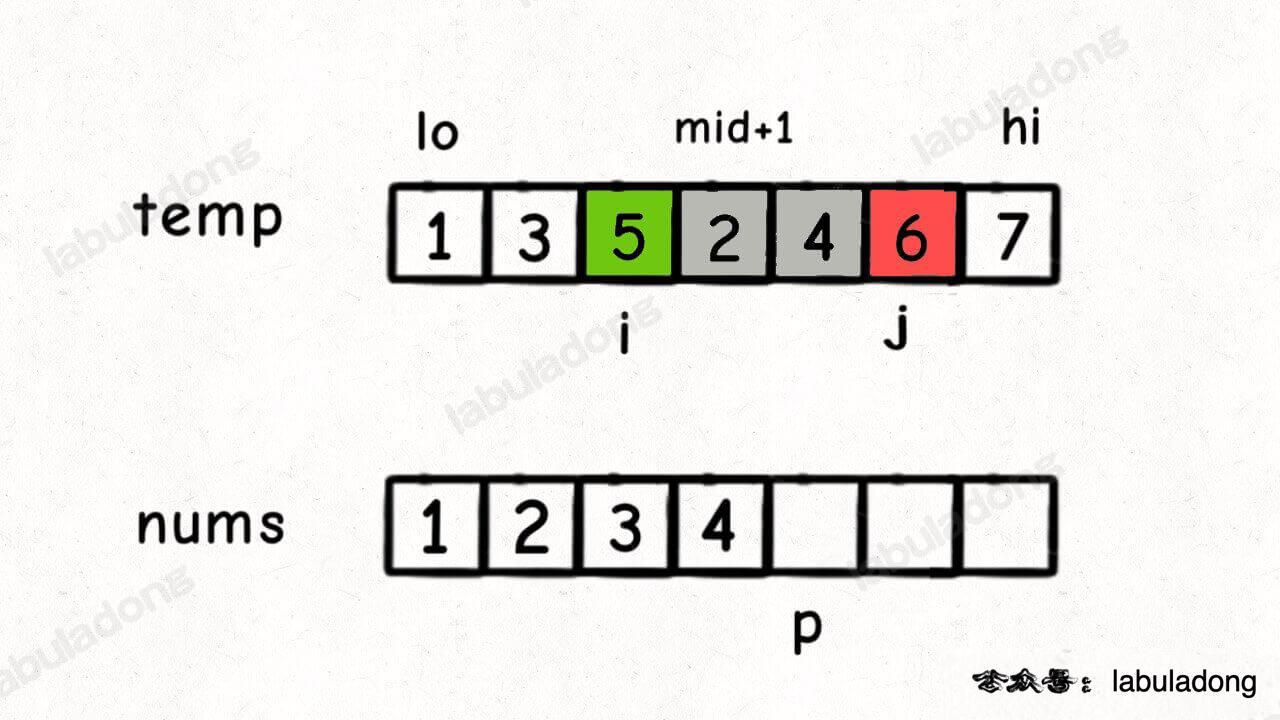
把?temp[i]?放到?nums[p]?上时,我们不仅知道?temp[i] < temp[j],还能确定?左闭右开区间?[mid + 1, j)?中的元素都是?temp[i]?右侧的、较小的元素。
换句话说,在对?
nuns[lo..hi]?合并的过程中,每当执行?nums[p] = temp[i]?时,就可以确定?temp[i]?这个元素后面比它小的元素个数为?j - mid - 1。
?count应当不断被累加,因为每次递归时,累加的都是新的右侧的数组中比nums[p]小的元素数量。
493. 翻转对
class Solution {
public:
int reversePairs(vector<int>& nums) {
res = 0;
temp.resize(nums.size());
Sort(nums, 0, nums.size() - 1);
return res;
}
private:
int res;
// 初始化一个辅助数组,避免递归时内存频繁分配释放
vector<int> temp;
void Sort(vector<int>& nums, int left, int right) {
// 只剩下一个元素,无需继续排序
if (left == right) {
return;
}
int mid = left + (right - left) / 2;
// 排序左侧数组[left, mid]
Sort(nums, left, mid);
// 排序右侧数组[mid + 1, right]
Sort(nums, mid + 1, right);
// 将有序的左右数组按顺序合并
Merge(nums, left, mid, right);
}
void Merge(vector<int>& nums, int left, int mid, int right) {
// 把 nums[left, right] 复制到辅助数组中,以便合并后的结果能够直接存入 nums
for (size_t i = left; i <= right; ++i) temp[i] = nums[i];
// 对两个有序数组,判断左侧元素nums[i] > 2*nums[j]是否成立
// 由于数组有序,可以优化统计效率:维护左闭右开区间 [mid+1, end) 中的元素乘 2 小于 nums[i]
int end = mid + 1;
for (size_t i = left; i <= mid; ++i) {
while (end <= right && (long)nums[i] > 2 * (long)nums[end]) end++;
res += end - mid - 1;
}
// 利用双指针技巧,合并两个有序数组
int left_p = left, right_p = mid + 1;
for (size_t p = left; p <= right; ++p) {
// 左侧数组已经merge完毕,只需要移动右侧数组的指针
if (left_p == mid + 1) nums[p] = temp[right_p++];
// 右侧数组已经merge完毕,只需要移动左侧数组的指针
else if (right_p == right + 1) nums[p] = temp[left_p++];
// 升序:右侧数比左侧数小,加入右侧元素
else if (temp[left_p] > temp[right_p]) nums[p] = temp[right_p++];
// 升序:左侧数比右侧数小,加入左侧元素
else nums[p] = temp[left_p++];
}
}
};本题所在Merge函数中添加了一段代码,在两个有序数组内,寻找右侧数组小于左侧数组当前元素的一半的元素数量。
【这种i<j,或寻找右侧/左侧元素个数的问题,都可以用分治思想解决,都可以借助于归并排序的模板】
327. 区间和的个数[*]
class Solution {
public:
int countRangeSum(vector<int>& nums, int lower, int upper) {
res = 0;
this->lower = lower;
this->upper = upper;
temp.resize(nums.size() + 1, 0);
preSum.resize(nums.size() + 1, 0);
for (size_t i = 0; i < nums.size(); ++i) preSum[i + 1] = preSum[i] + nums[i];
Sort(preSum, 0, preSum.size() - 1);
return res;
}
private:
int res;
int lower;
int upper;
// 前缀和数组,用于快速计算区间和。用long类型防止和溢出
vector<long> preSum;
// 初始化一个辅助数组,避免递归时内存频繁分配释放
vector<long> temp;
void Sort(vector<long>& nums, int left, int right) {
// 只剩下一个元素,无需继续排序
if (left == right) {
return;
}
int mid = left + (right - left) / 2;
// 排序左侧数组[left, mid]
Sort(nums, left, mid);
// 排序右侧数组[mid + 1, right]
Sort(nums, mid + 1, right);
// 将有序的左右数组按顺序合并
Merge(nums, left, mid, right);
}
void Merge(vector<long>& nums, int left, int mid, int right) {
// 把 nums[left, right] 复制到辅助数组中,以便合并后的结果能够直接存入 nums
for (size_t i = left; i <= right; ++i) temp[i] = nums[i];
// 维护左闭右开区间 [start, end) 中的元素和 nums[i] 的差在 [lower, upper] 中
int start = mid + 1;
int end = mid + 1;
for (size_t i = left; i <= mid; ++i) {
// 如果 nums[i] 对应的区间是 [start, end),
// 那么 nums[i+1] 对应的区间一定会整体右移,类似滑动窗口
while (start <= right && nums[start] - nums[i] < lower) start++;
while (end <= right && nums[end] - nums[i] <= upper) end++;
res += end - start;
}
// 利用双指针技巧,合并两个有序数组
int left_p = left, right_p = mid + 1;
for (size_t p = left; p <= right; ++p) {
// 左侧数组已经merge完毕,只需要移动右侧数组的指针
if (left_p == mid + 1) nums[p] = temp[right_p++];
// 右侧数组已经merge完毕,只需要移动左侧数组的指针
else if (right_p == right + 1) nums[p] = temp[left_p++];
// 升序:右侧数比左侧数小,加入右侧元素
else if (temp[left_p] > temp[right_p]) nums[p] = temp[right_p++];
// 升序:左侧数比右侧数小,加入左侧元素
else nums[p] = temp[left_p++];
}
}
};首先,看到区间和时,要想到利用前缀和数组进行快速计算。于是就可以对前缀和数组进行归并排序,在merge函数中统计区间和满足要求的个数。
由于merge时两个数组是有序的,可以进行效率优化,即维护一个滑动窗口,让窗口中的元素和?nums[i]?的差落在?[lower, upper]?中。
归并排序算法,递归的?
sort?函数就是二叉树的遍历函数,而?merge?函数就是在每个节点上做的事情。在每个节点上做事时都可以满足以下两点:操作两个有序数组、左侧的元素在原数组中的下标一定小于右侧的元素。尤其是第二点,对于上述“右侧元素小于当前元素数目”、“翻转对”和“区间和(利用前缀和计算时要求j>i)”等问题适用。
?