开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 算法与数据结构——动态规划（java）（b站左程云课程笔记总结） -> 正文阅读

[数据结构与算法]算法与数据结构——动态规划（java）（b站左程云课程笔记总结）

动态规划

从递归套路改到动态规划

暴力递归——>记忆化搜索——>严格表结构——>精致版严格表结构

技巧

在设置严格表的时候尽量不要去考虑原题意

机器人走路问题

给定一个大于1的整数N，表示一共有1到N个位置

一个整数s(1-N)位置表示机器人的起始位置

一个整数e(1-N)位置表示机器人要去的终点位置

一个整数k表示机器人必须走k步

机器人每步必须走，每次走一步，在1位置只能往右走，在N位置只能往左走

问：机器人在必须走k步的情况下，从s到e一共有几种走法？

递归试法

public int walkWays(int N,int E,int S,int K){
    return f(N,E,K,S);
}


//最终目标E
//还剩rest步要走
//当前在cur位置
//返回方法数
public int f(int N,int E,int rest,int cur){
    if(rest==0){//终止条件
        return cur==E?1:0;
    }
    if(cur==1){
        return f(N,E,rest-1,2);
    }
    if(cur==N){
        return f(N,E,rest-1,N-1);
    }
    return f(N,E,rest-1,cur-1)+f(N,E,rest-1,cur+1);
}

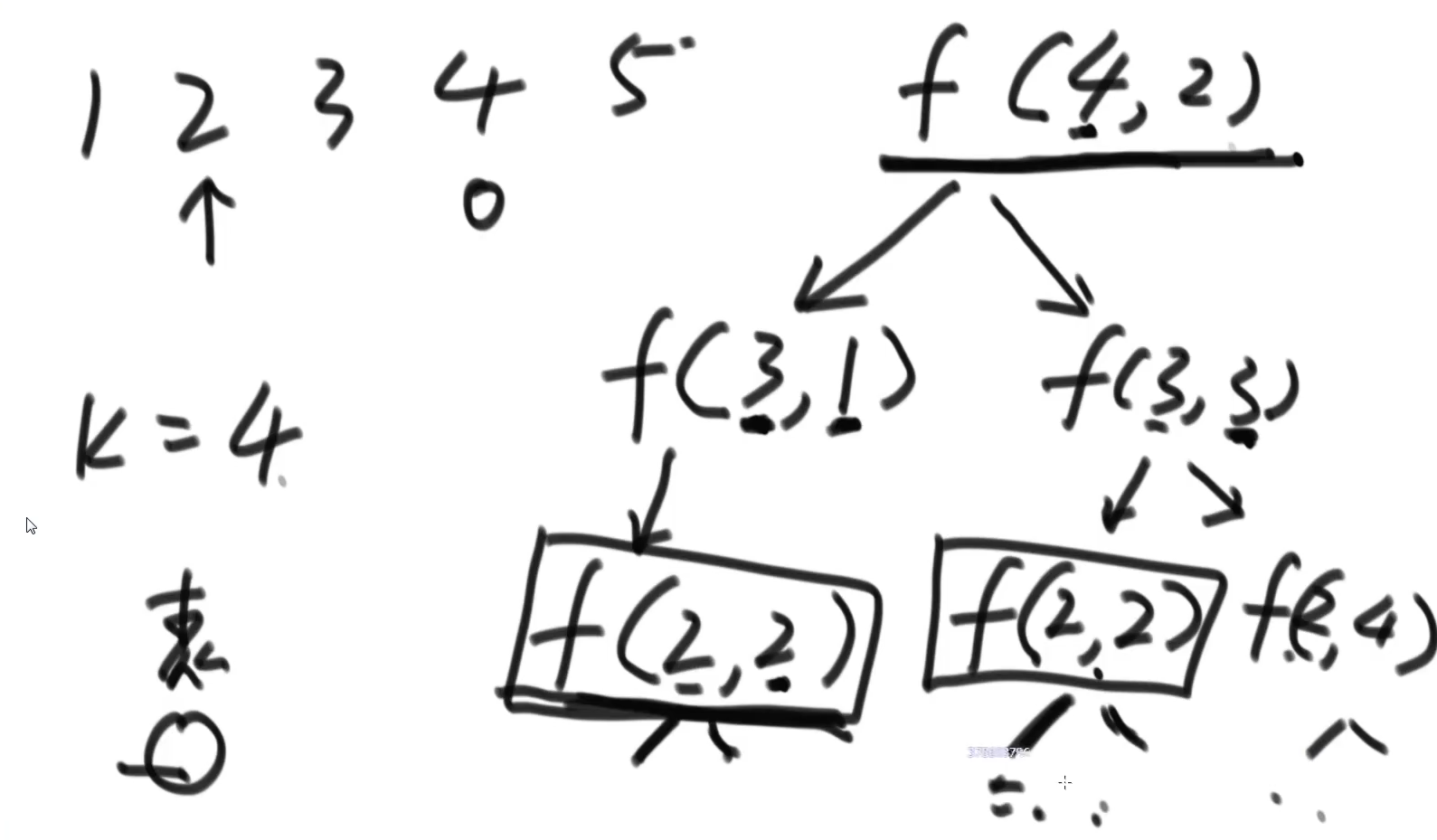
时间复杂度：看作二叉树，树的高度是k，O(2^k)

递归过程有重复的过程

f(2,2)之前已经求解过，后续可以省略，直接拿结果

可变参数一旦固定，结果确定，即无后效性尝试（之前的尝试不影响）

如何从递归版本进化到记忆化搜索过程？

public int walkWays2(int N,int E,int S,int K){
    int[][] dp=new int[K+1][N+1];//两个可变参数，构造二维数组，数组大小保证够用且不浪费过多空间即可
    for(int i=0;i<=K;i++){
        for(int j=0;j<=N;j++){
            dp[i][j]=-1;//先把dp中的所有值改成-1（默认是0）
        }
    }
    return f2(N,E,K,S,dp);//加一个参数dp
}

public int f2(int N,int E,int rest,int cur,int[][] dp){
    if(dp[rest][cur]!=-1){//查缓存
        return dp[rest][cur];//命中缓存
    }
    //缓存没命中
    if(rest==0){//终止条件
        dp[rest][cur]=cur==E?1:0;
    }else if(cur==1){
        dp[rest][cur]=f2(N,E,rest-1,2);
    }else if(cur==N){
        dp[rest][cur]=f2(N,E,rest-1,N-1);
    }else{
        dp[rest][cur]=f2(N,E,rest-1,cur-1)+f2(N,E,rest-1,cur+1);
    }
    return dp[rest][cur];
}

时间复杂度：二维表的规模是KxN，每个格子最多算一遍，计算过程时间复杂度是O(1)，总时间复杂度为O(k*N)

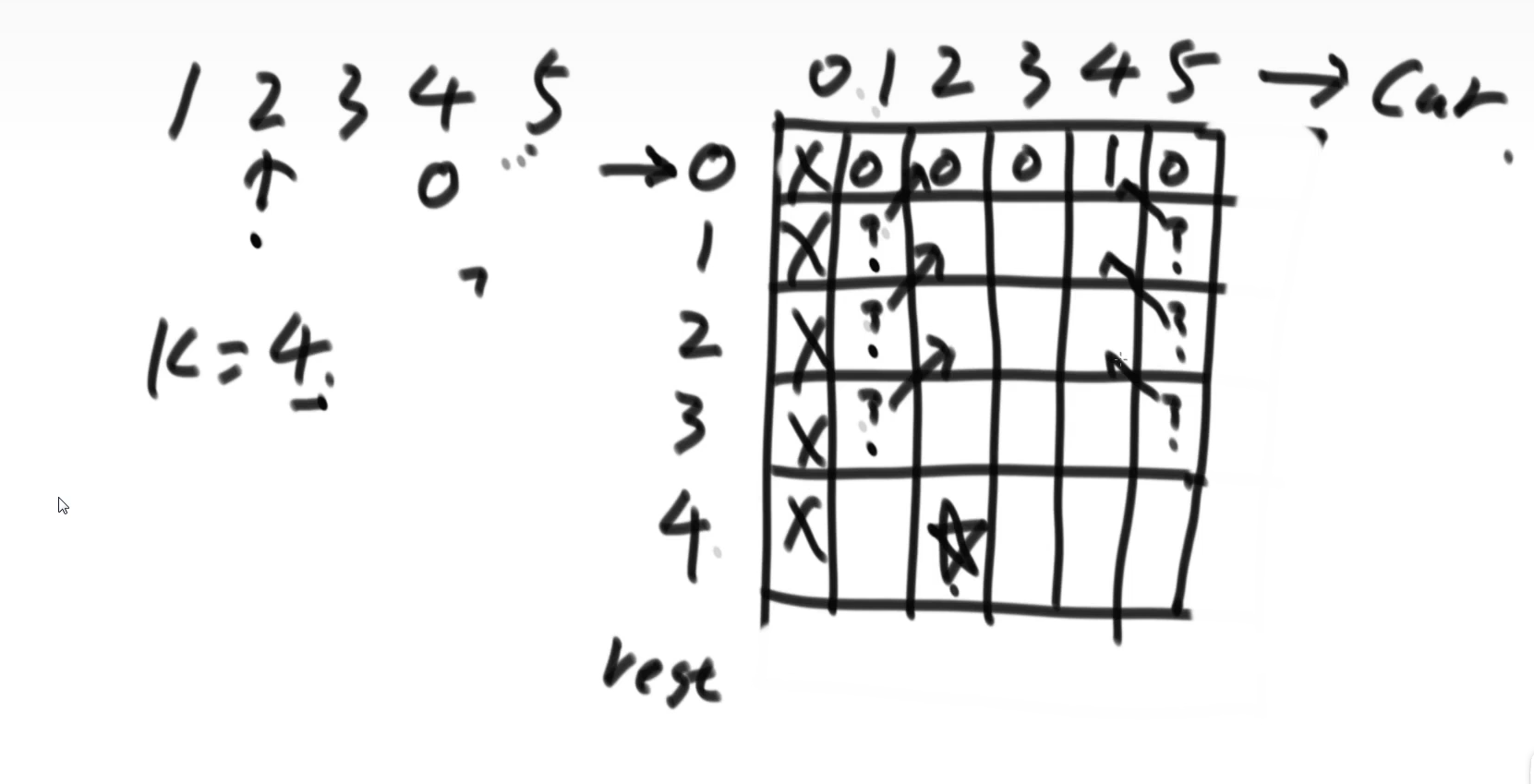
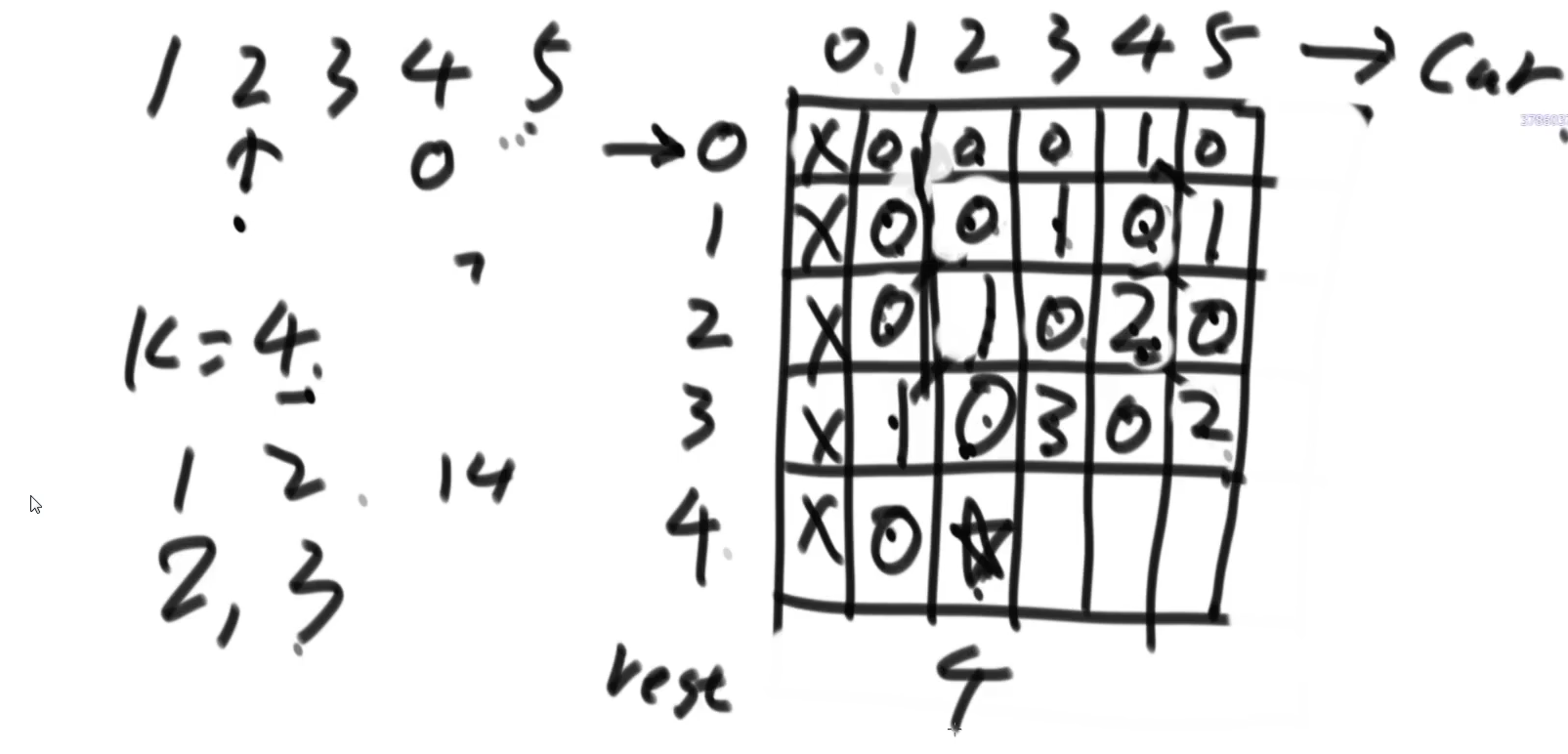
严格表结构的动态规划

base case终止条件可以得到第一行的值

两边位置分别依赖右上角和左上角的值

中间位置依赖左上角和右上角的值

最终要得到星号位置上的值（最终要得到的可以看作是初始的时候的条件）

记忆化搜索不去整理位置之间的依赖关系，只是一个傻缓存

而严格表动态规划是要去整理依赖关系的

对于这题来说记忆化搜索和严格表动态规划时间复杂度一样

public int walkWays3(int N,int E,int S,int K){
    int[][] dp=new int[K+1][N+1];
    dp[0][E]=1;
    for(int i=1;i<=k;i++){
        for(int j=1;j<=N;j++){
            if(j==1){
                dp[i][j]=dp[i-1][2];
            }else if(j==N){
                dp[i][j]=dp[i-1][N-1];
            }else{
                dp[i][j]=dp[i-1][j-1]+dp[i-1][j+1];
            }
        }
    }
    return dp[k][S];
}

硬币面值选择问题

给定一个数组里面放的是正数，表示每一个硬币的面值

给定一个数aim，要求在数组中选择硬币，数值加起来刚好等于该数，问最少拿几个硬币可以完成

尝试

public int min1(int[] arr,int aim){
    return f1(arr,0,aim);
}

public int f1(int[] arr,int index,int rest){
    if(rest<0){
        return -1;
    }
    if(rest==0){
        return 0;
    }
    if(index==arr.length){
        return -1;
    }
    int p1=f1(arr,index+1,rest);
    int p2=f1(arr,index+1,rest-arr[index]);
    if(p1==-1&&p2==-1){
        return -1;
    }else{
        if(p1==-1){
            return p2+1;
        }
        if(p2==-1){
            return p1;
        }
        return Math.min(p1,p2+1);
    }
}

记忆化搜索

public int min2(int[] arr,int aim){
    int[][] dp=new int[arr.length+1][aim+1];
    for(int i=0;i<=arr.length;i++){
        for(int j=0;j<=aim;j++){
            dp[i][j]=-2;
        }
    }
    return f2(arr,0,aim,dp);
}

public int f2(int[] arr,int index,int rest,int[][] dp){
    if(rest<0){
        return -1;
    }
    if(dp[index][rest]!=-2){
        return dp[index][rest];
    }
    if(rest==0){
        dp[index][rest]=0;
    }else if(index==arr.length){
        dp[index][rest]=-1;
    }else{
        int p1=f2(arr,index+1,rest,dp);
        int p2=f2(arr,index+1,rest-arr[index],dp);
        if(p1==-1&&p2==-1){
            dp[index][rest]=-1;
        }else{
            if(p1==-1){
                dp[index][rest]=p2+1;
            }
            if(p2==-1){
                dp[index][rest]=p1;
            }
            dp[index][rest]=Math.min(p1,p2+1);
        }
    }
    return dp[index][rest];
}

严格表

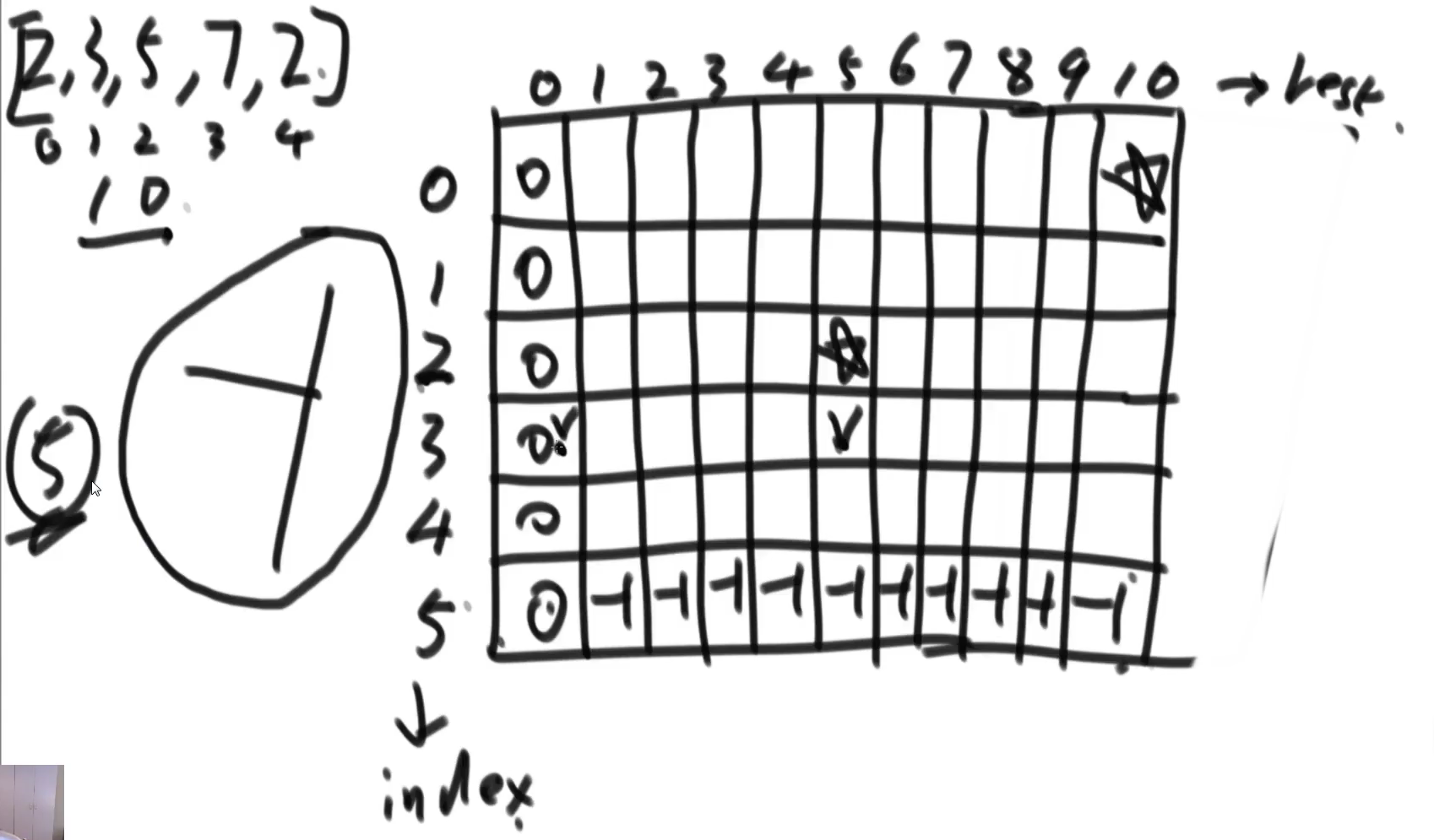
public int min3(int[] arr,int aim){
    if (arr == null || arr.length == 0 || aim < 0) {
        return -1;
    }
    int[][] dp=new int[arr.length+1][aim+1];
    int N=arr.length;
    //第一列都是0不用设置（默认都是0）
    for(int col=1;col<=aim;col++){
        dp[N][col]=-1;
    }
    for(int i=N-1;i>=0;i--){//从底向上计算每一行
        for(int rest=0;rest<=aim;rest++){//每一行从左往右
            dp[i][rest]=-1;//初始时先设置为无效
            if(dp[i+1][rest]!=-1){//下面的值有效
                dp[i][rest]=dp[i+1][rest];//先设置为下面的值
            }
            //左边的位置不越界并且有效
            if(rest-arr[i]>=0&&dp[i][rest-arr[i]]!=-1){
                if(dp[i][rest]==-1){//下面的值无效
                    dp[i][rest]=dp[i][rest-arr[i]]+1;//这里不要漏了+
                }else{//下面的值有效
                    dp[i][rest]=Math.min(dp[i][rest],dp[i][rest-arr[i]]+1);
                }
            }
        }
    }
    return dp[0][aim];
}

严格表指定步骤：

根据可变参数设置dp
最终要的答案在dp的哪个位置
base case设置dp中一部分的值
dp中普通位置的依赖关系
dp中值设置的顺序

拿牌游戏

尝试版本

public int win(int[] arr){
    if(arr==null||arr.length==0){
        return 0;
    }
    return Math.max(f(arr,0,arr.length-1),s(arr,0,arr.length-1));
}

//先手拿
public int f(int[] arr,int i,int j){
    if(i==j){//base case
        return arr[i];
    }
    return Math.max(arr[i]+s(arr,i+1,j),arr[j]+s(arr,i,j-1));
}

//后手拿
public int s(int[] arr,int i,int j){
    if(i==j){
        return 0;
    }
    return Math.min(f(arr,i+1,j),f(arr,i,j-1));//这里后手拿的时候相当于是先手拿对方拿过的，但先手会把对后手最不利的方式给到后手
}

记忆化搜索

在f函数、s函数中加缓存

动态规划（严格表）(范围型题目)

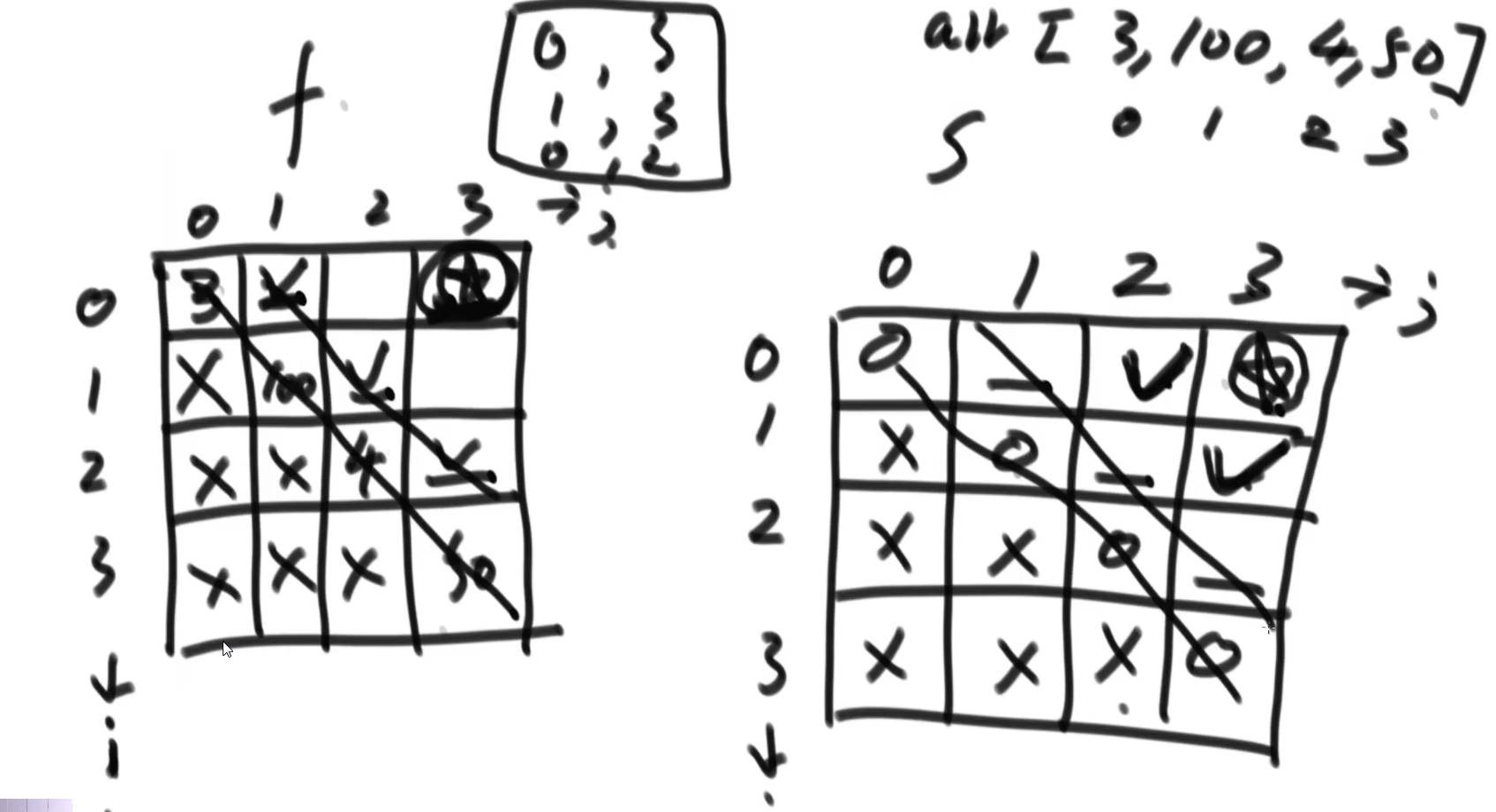
可变参数有i和j，两个参数的范围都是数组的长度，二维数组为正方形

且因为i<j，两个表都有半区都是没用的

通过base case可以得到对角线上两个表的值

普遍情况是看另外一个表的左边和下边

整体顺序从下往上，从左往右，也可以是根据左边的对角线推出右边的对角线

public int win2(int[] arr){
    if(arr==null||arr.length==0){
        return 0;
    }
    int[][] f=new int[arr.length][arr.length];
    int[][] s=new int[arr.length][arr.length];
    for(int j=0;j<arr.length;j++){
        f[j][j]=arr[j];
        for(int i=j-1;i>=0;i--){
            f[i][j]=Math.max(arr[i]+s[i+1][j],arr[j]+s[i][j-1]);
            s[i][j]=Math.min(f[i+1][j],f[i][j-1]);
        }
    }
    return Math.max(f[0][arr.length-1],s[0][arr.length-1]);
}

马踏棋盘问题

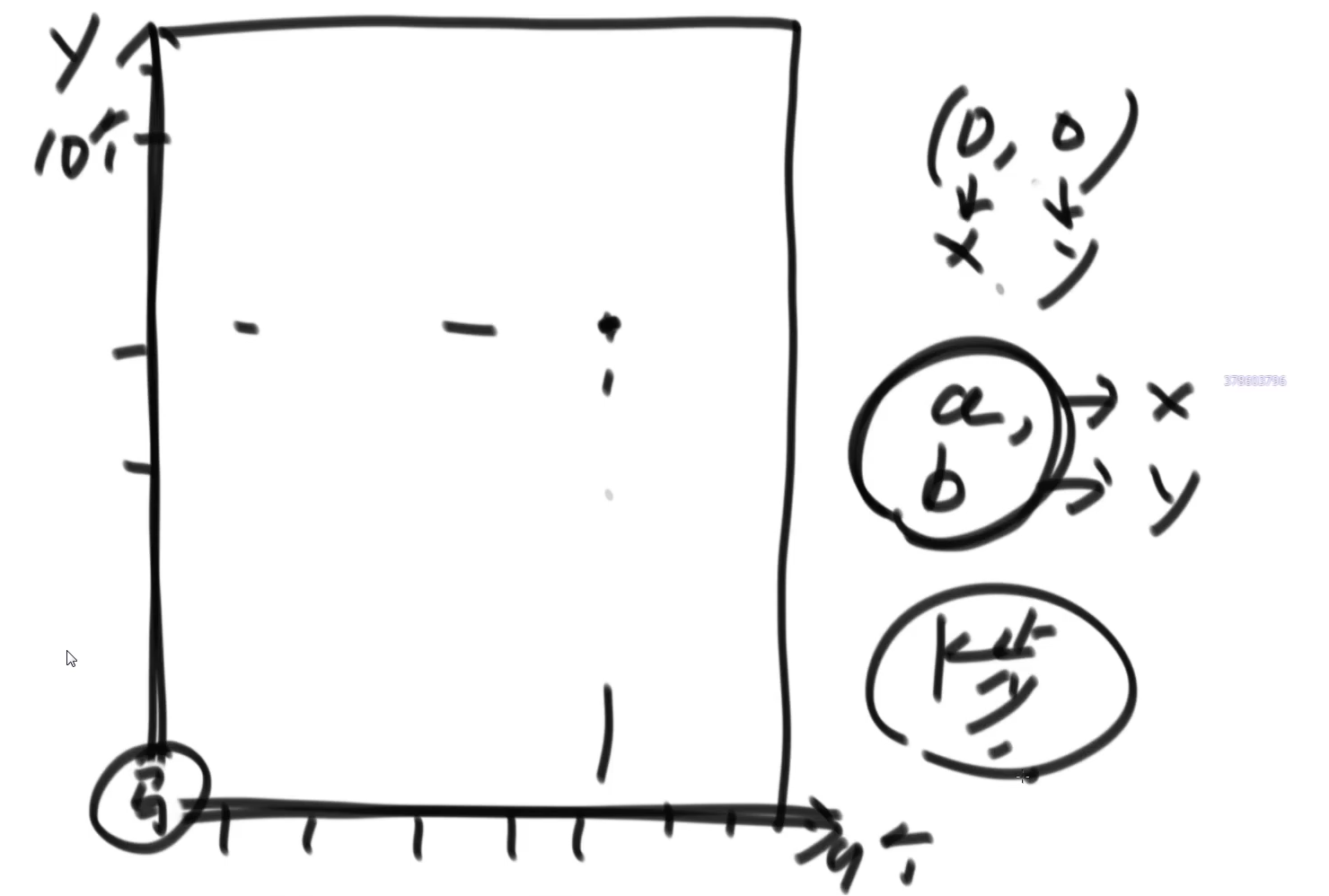
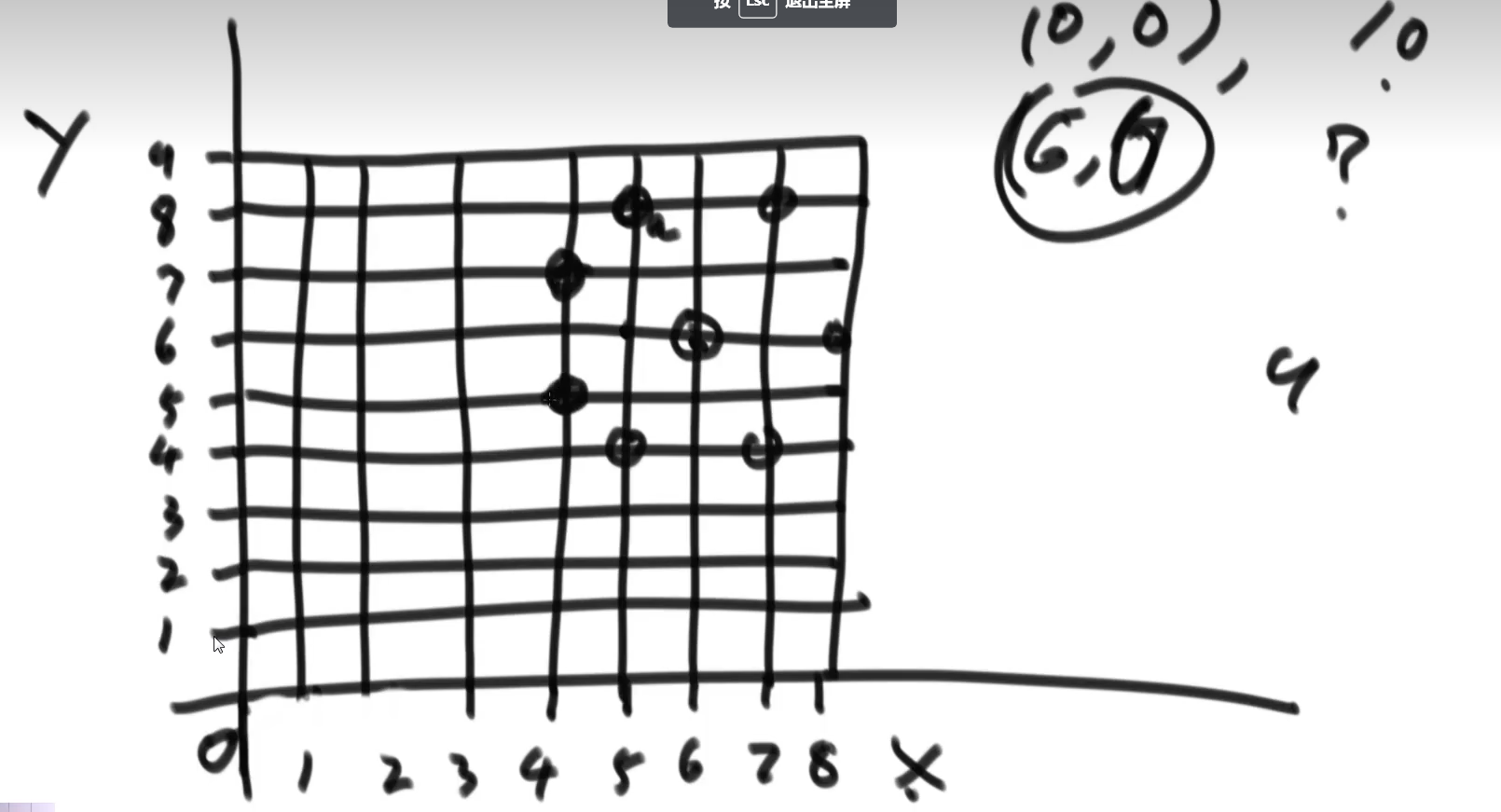
中国象棋棋盘（横9纵10），马一开始在（0,0）位置，要去到（a,b）位置，一定要走k步，有几种走法？

反着理解，从(x,y)到(0,0)十步可以看作是(0,0)到(x,y)附近的八个点且k-1步的方法数

public int process(int x,int y,int step){
    if(x<0||x>8||y<0||y>9){
        return 0;
    }
    if(step==0){
        return (x==0&&y==0)?1:0;//这里反着写可以少两个固定参数
    }
    return process(x-1,y+2,step-1)+process(x+1,y+2,step-1)+process(x-1,y-2,step-1)+process(x+1,y-2,step-1)+process(x+2,y-1,step-1)+process(x-2,y-1,step-1)+process(x+2,y+1,step-1)+process(x-2,y+1,step-1);
}

怎么改？

三个参数，三维表

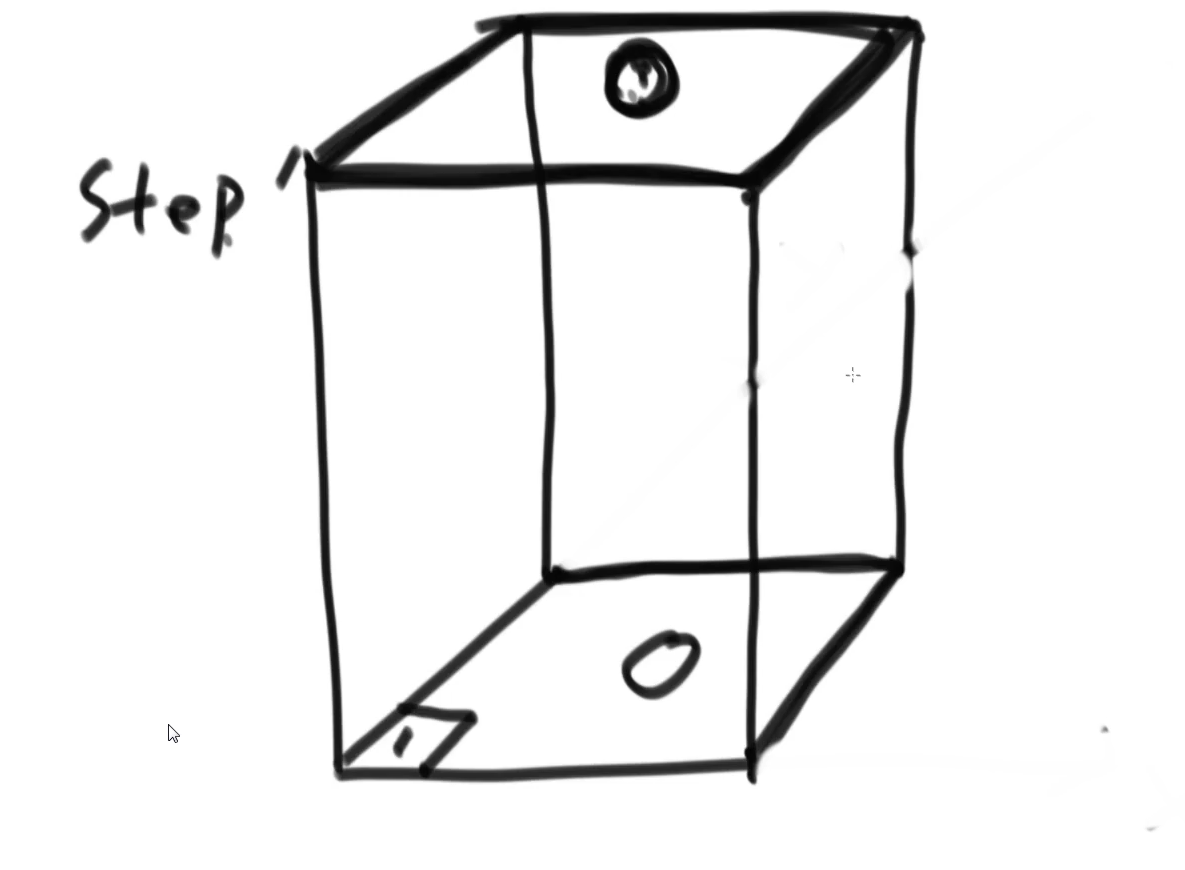
把step设置为高度

想要获得的值的地方是最上面一层的(x,y)位置

base case整个长方体外面的都是0，最底层的(0,0)位置是1，其他位置是0

根据子过程可以得知从下往上一层一层推可以推出来整个正方体(step-1)，最后到最上面一层的(x,y)位置

public int dpWays(int x,int y,int step){
    if(x<0||x>8||y<0||y>9||step<0){
        return 0;
    }
    int[][][] dp=new int[9][10][step+1];
    dp[0][0][0]=1;
    for(int h=1;h<=step;h++){
        for(int r=0;r<9;r++){//这里x和y的遍历顺序不影响结果
            for(int c=0;c<10;c++){
                dp[r][c][h]+=getValue(dp,r-1,c+2,h-1);
                dp[r][c][h]+=getValue(dp,r+1,c+2,h-1);
                dp[r][c][h]+=getValue(dp,r-1,c-2,h-1);
                dp[r][c][h]+=getValue(dp,r+1,c-2,h-1);
                dp[r][c][h]+=getValue(dp,r-2,c+1,h-1);
                dp[r][c][h]+=getValue(dp,r+2,c+1,h-1);
                dp[r][c][h]+=getValue(dp,r-2,c-1,h-1);
                dp[r][c][h]+=getValue(dp,r+2,c-1,h-1);
            }
        }
    }
    return dp[x][y][step];
}


//判断是否越界
public int getValue(int[][][] dp,int row,int col,int step){
    if(row<0||row>8||col<0||col>9){
        return 0;
    }
    return dp[row][col][step];
}

鲍勃生存游戏

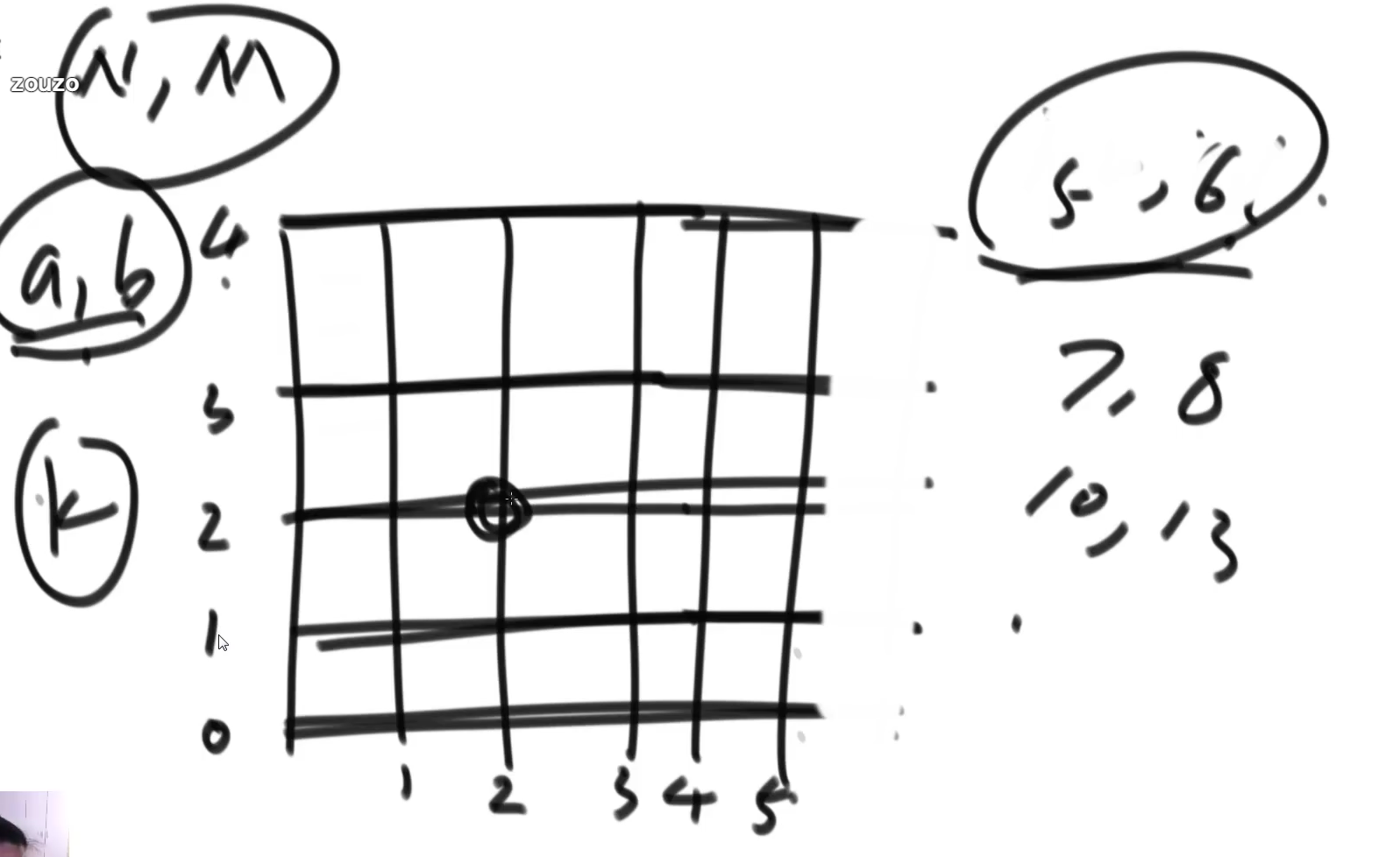
给定一个N*M的矩阵，现在鲍勃在(a,b)位置，鲍勃一定要走k步，一旦鲍勃走完k步不在这个矩阵就认为鲍勃死了，问鲍勃能生存下来的概率是多少？

鲍勃生存下来的概率是鲍勃的生存方法数/4的k次方

public String bob1(int N,int M,int i,int j,int K){
    long all=(long)Math.pow(4,k);
    long live=process(N,M,i,j,K);
    long gcd=gcd(all,live);//求最大公约数
    return String.valueOf((live/gcd)+"/"+(all/gcd));//把分数化成最简
}


//N*M的区域，鲍勃从(row,col)位置出发，走rest步之后，获得的生存方法数
public long  process(int N,int M,int row,int col,int rest){
    if(row<0||row==N||col<0||col==M){
        return 0;
    }
    if(rest==0){
        return 1;
    }
    return process(N,M,row-1,col,rest-1)+process(N,M,row+1,col,rest-1)+process(N,M,row,col+1,rest-1)+process(N,M,row,col-1,rest-1);
}

三维：

要的是最高层的(i,j)位置

base case是第一层的全部位置都是1

从最底下一层往上推

public String bob2(int N,int M,int i,int j,int K){
    int[][][] dp=new int[N+2][M+2][K+1];
    for(int row=1;row<=N;row++){
        for(int col=1;col<=M;col++){
            dp[row][col][0]=1;
        }
    }
    for(int rest=1;rest<=K;rest++){
        for(int row=1;row<=N;row++){
            for(int col=1;col<=M;col++){
                dp[row][col][rest] = dp[row - 1][col][rest - 1];
                dp[row][col][rest] += dp[row + 1][col][rest - 1];
                dp[row][col][rest] += dp[row][col - 1][rest - 1];
                dp[row][col][rest] += dp[row][col + 1][rest - 1];
            }
        }
    }
    long all = (long) Math.pow(4, K);
    long live = dp[i + 1][j + 1][K];
    long gcd = gcd(all, live);
    return String.valueOf((live / gcd) + "/" + (all / gcd));
}

个人感觉这道题目是有问题的，如果题目设定是一旦鲍勃走完k步不在这个矩阵就认为鲍勃死了，那这里dp数组应该至少设置成(N+2k)x(M+2k)x(K+1)吧，要不然会越界

完全背包问题

给定一个数组，里面存放的是货币的面值，无重复值，数组中的货币数无限，给定一个数aim，求拿数组中的货币一共有几种拿法可以使总和为aim

public int way1(int[] arr,int aim){
    return process(arr,0,aim);
}

public int process(int[] arr,int index,int rest){
    if(index==arr.length){
        return rest==0?1:0;
    }
    int ways=0;
    for(int num=0;arr[index]*num<=rest;num++){
        ways+=process(arr,index+1,rest-arr[index]*num);
    }
    return ways;
}

改动态规划

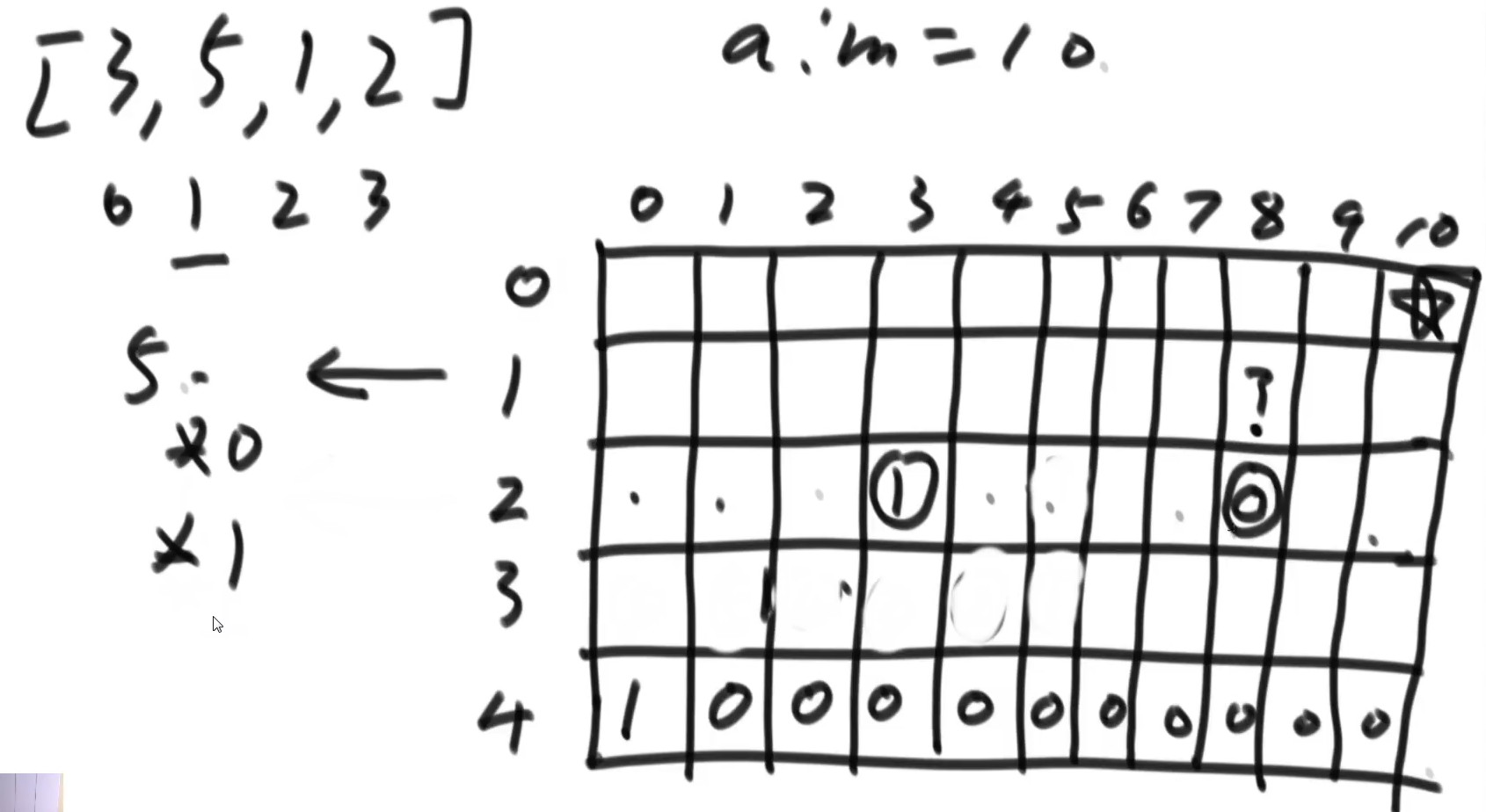
两个可变参数

base case最后一行第一个是1，其他是0

整体顺序从下往上，从左到右还是从右到左没所谓

public int way2(int[] arr,int aim){
    if(arr==null||arr.length==0){
        return 0;
    }
    int[][] dp=new int[arr.length+1][aim+1];
    dp[arr.length][0]=1;
    for(int index=arr.length-1;index>=0;index--){
        for(int rest=0;rest<=aim;rest++){
            int ways=0;
            for(int num=0;num*arr[index]<=rest;num++){
                ways+=dp[index+1][rest-arr[index]*num];
            }
            dp[index][rest]=ways;
        }
    }
    return dp[0][aim];
}

时间复杂度估计

表格是N*aim的大小，但是每次处理过程不是O(1)，有枚举的行为发生，最差的情况是枚举aim次，因此时间复杂度是O(N*aim^2)

枚举行为有必要吗？

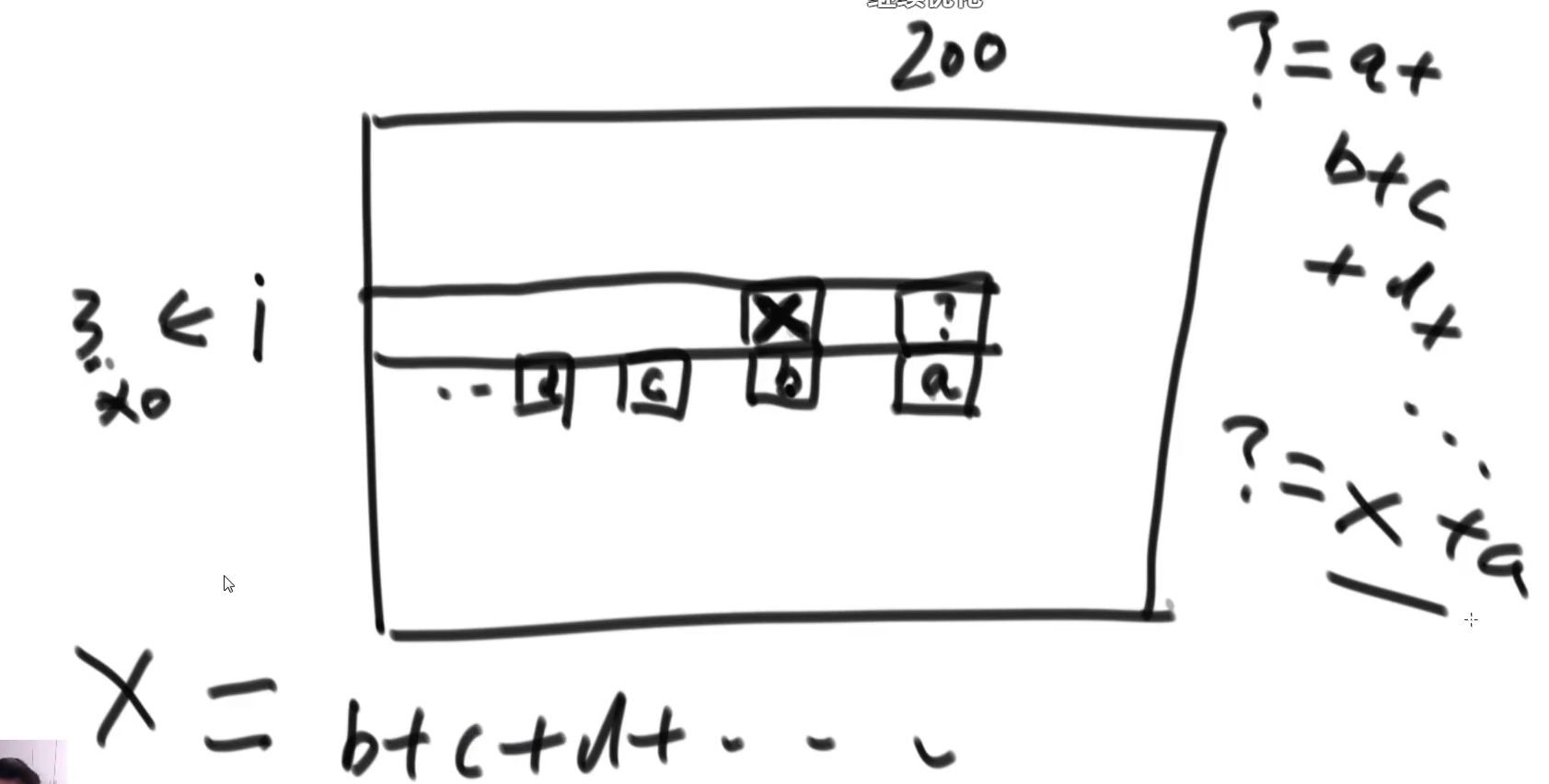
精致版严格表

斜率优化

问号的位置是x的位置的值＋a，不用每次都去计算，这样会有重复计算的过程

这个过程不要去想意义，从dp数组，利用观察、统计的角度去思考就行了

public int way2(int[] arr,int aim){
    if(arr==null||arr.length==0){
        return 0;
    }
    int[][] dp=new int[arr.length+1][aim+1];
    dp[arr.length][0]=1;
    for(int index=arr.length-1;index>=0;index--){
        for(int rest=0;rest<=aim;rest++){
            dp[index][rest]=dp[index+1][rest];
            if(rest-arr[index]>=0){//这个时候顺序应该就有要求是从左往右
                dp[index][rest]+=dp[index][rest-arr[index]];//注意这里后面的index不用加一 加的是前一个的
            }
        }
    }
    return dp[0][aim];
}

力扣518

给你一个整数数组 coins 表示不同面额的硬币，另给一个整数 amount 表示总金额。

请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额，返回 0 。

假设每一种面额的硬币有无限个。

题目数据保证结果符合 32 位带符号整数。

class Solution {
    public int change(int amount, int[] coins) {
        int[][] dp=new int[coins.length+1][amount+1];
        dp[coins.length][0]=1;
        for(int index=coins.length-1;index>=0;index--){
            for(int rest=0;rest<=amount;rest++){
                dp[index][rest]=dp[index+1][rest];
                if(rest-coins[index]>=0){
                    dp[index][rest]+=dp[index][rest-coins[index]];
                }
            }
        }
        return dp[0][amount];
    }
}