?
?个人主页:欢迎大家光临——>沙漠下的胡杨
? 各位大帅哥,大漂亮
?如果觉得文章对自己有帮助
?可以一键三连支持博主
?你的每一分关心都是我坚持的动力
?
??: 本期重点:
??希望大家每天都心情愉悦的学习工作。?
目录
??: 本期重点:非比较排序(计数排序和基数排序)
在我们之前的讲解中,我们学到了大多数的比较排序,今天我们主要学一下非比较排序。
计数排序:
? ? ? ? 计数排序是一个非基于比较的排序算法,该算法于1954年由 Harold H. Seward 提出。它的优势在于在对一定范围内的整数排序时,它的复杂度为Ο(n+k)(其中k是整数的范围),快于任何比较排序算法。?当然这是一种牺牲空间换取时间的做法,而且O(k)>O(n*log(n))的时候其效率反而不如基于比较的排序(基于比较的排序的时间复杂度在理论上的下限是O(n*log(n)), 如归并排序,堆排序)
排序思想:
1. 确定开辟的空间大小(一般为数据中的最大值 - 最小值的差值)。、
2.?确定对应关系。
3. 把数据对应关系的数组下标自增。
4. 根据队形关系拷贝数据。
计数排序图示分析:
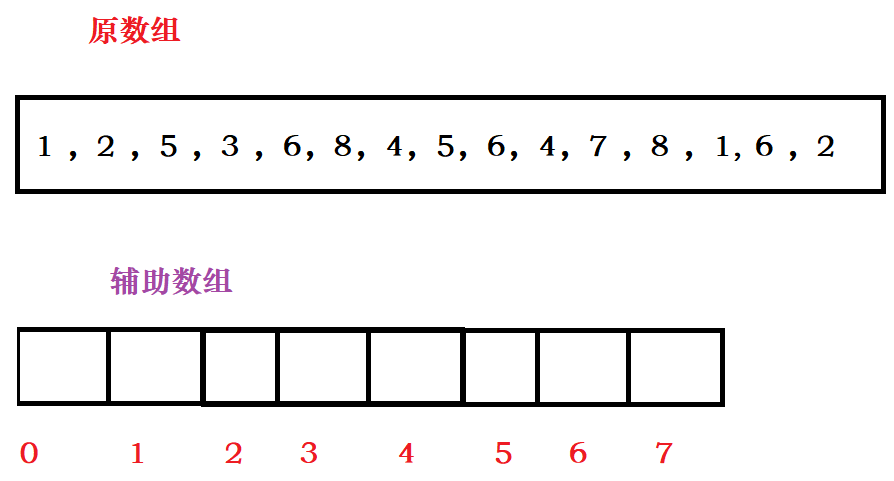
首先我们有原数组,还要开辟一个辅助数组。并且辅助数组的大小是根据原数组中的数据的最大值—最小值决定的。下面数组中的值都在 1 到 8之间,所以我们辅助数组开辟 8?个大小的空间,其中 原数组中 1?对应辅助数组中下标 0 的位置,原数组中 8 数据,对应辅助数组下标为 7 的位置,刚开始时我们把辅助数据都为内存设置为0。
下面我们把数据根据对应关系写入辅助数组中去,1对应位置就是数组下标为0的位置,然后把辅助数组内的数据自增。8 对应下标为 7 的位置,然后把辅助数组内的数组自增。
写入完成后,我们根据辅助数组和原数组的对应关系,一个个的在写入原数组,其中辅助数组 0 下标对应的是 1 ,然后 0 下标的数据 2 表示写入两次?。同理,下标为辅助数组 7 下标对相应的是 8 ,辅助数组下标为 7 的数据为 2 ,表示写入 2 次 8。
? ?
代码实现:
void CountSort(int* a, int n)//计数排序 { //获取最大值和最小值 int max = a[0]; int min = a[0]; for (int i = 0; i < n; i++) { if (max < a[i]) { max = a[i]; } if (min > a[i]) { min = a[i]; } } //获取开辟的区间大小 int rang = max - min + 1; //开辟空间 int* count = (int*)malloc(sizeof(int)*rang); if (count == NULL) { perror("malloc fail"); exit(-1); } //把辅助数组的区间设置为0。 memset(count, 0, sizeof(int)*rang); //根据对应关系写入辅助数组 for (int i = 0; i < n; i++) { //写入时,根据对应关系一定是下标原数组数据减去最小值。 count[a[i] - min]++; } //根据对应关系写回原数组 int j = 0; //判断区间为是否结束 for (int i = 0; i < rang; i++) { //此时判断的是辅助数组的数据是否为0 while (count[i]--) { a[j++] = i + min; } } //释放空间 free(count); count = NULL; }
基数排序:
基数排序算法思想:
? ? 基数排序(radix sort)属于“分配式排序”(distribution sort),又称“桶子法”(bucket sort)或bin sort,顾名思义,将要排序的元素分配至某些“桶”中,以达到排序的作用,基数排序法是属于稳定性的排序,其时间复杂度为O (nlog(r)m),其中r为所采取的基数,而m为堆数,在某些时候,基数排序法的效率高于其它的稳定性排序法。
奇数排序实现流程:
1. 我们首先明确基数,一般是0~9这10个数字为基数。
2. 选取最大数的位数作为排序的次数。
3.然后根据个位上的数据排序,拷贝回原数组,再根据十位上的数据排序,拷贝回原数组(不足的位数补0,比如 2 ,2不到10,所以十位为 0?)
4.一直拷贝到最大数的最高位数停止,此时数据已经有序。
基数排序图示:
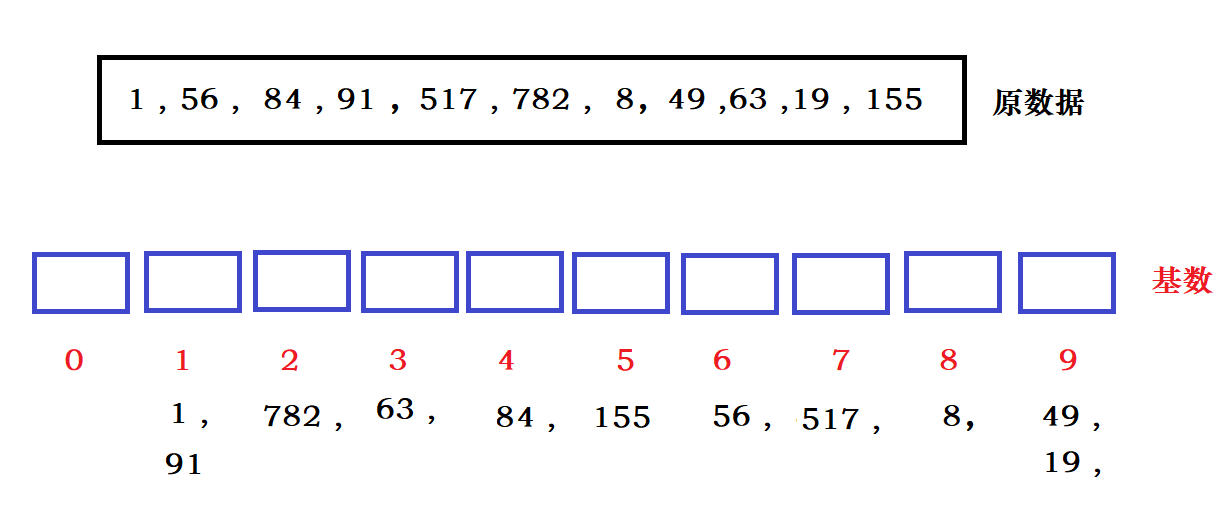
下面是一些随机数,然后我们排序,首先我们确定基数是 0~9 。然后我们确定最大数的最高位次是3,表示排序 3 次?。
下面我们按照个位上的数进行分配数据。?
?然后在进行回收数据,先放的数据先取出(先进先出):
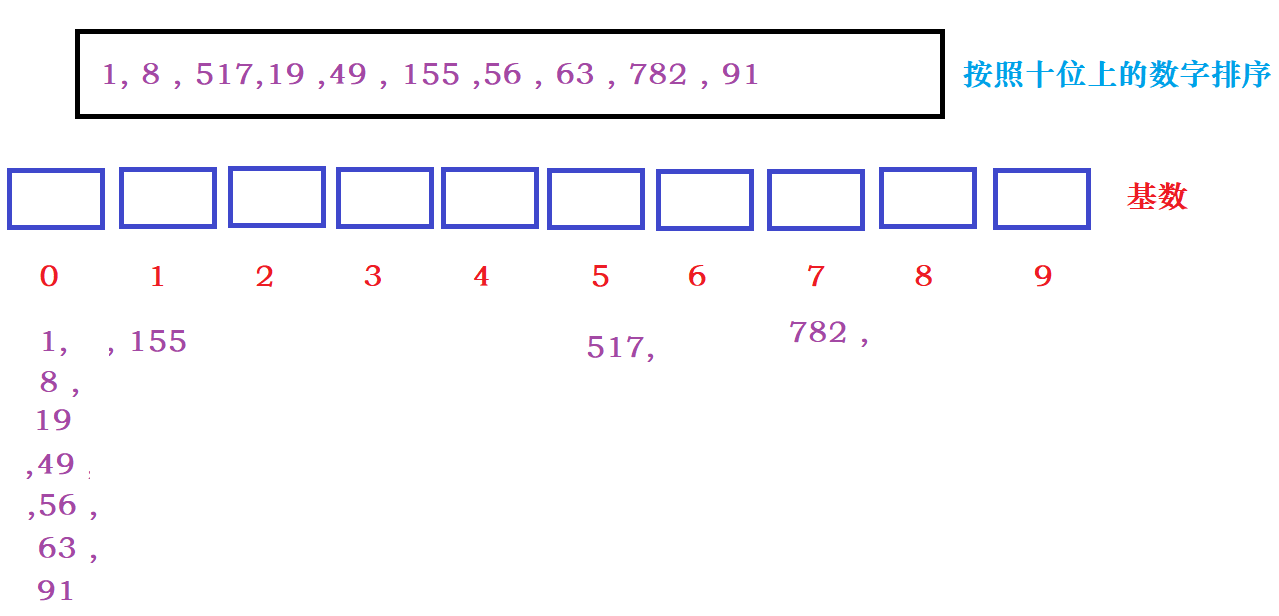
根据十位上的数据分发数据:
回收十位上排序好的数据:
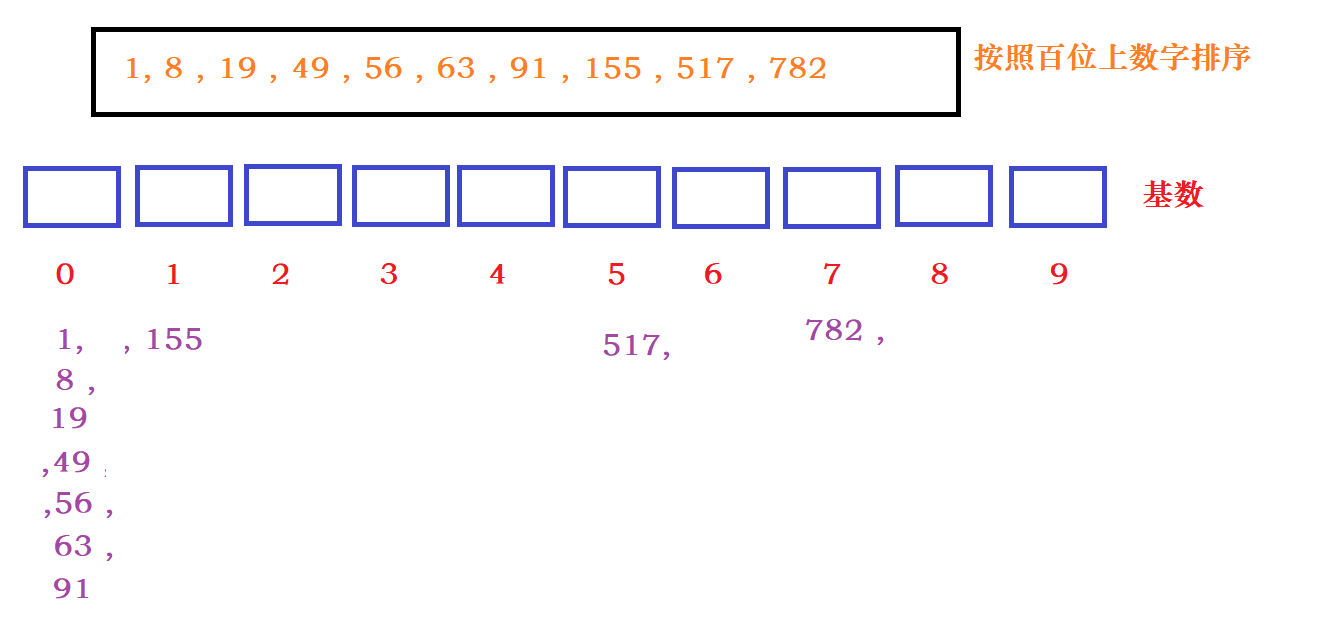
?根据百位上的数据分发:
在回收百位上排序好的数据:
因为最大的数只有百位,所以此时排序完成。
??
代码实现(用队列辅助实现):
//最大数据的位数,在数据量较小时,我们可以看出所以直接定义了最大的位数 #define K 3 //定义全局的10个队列,对应基数为0 ~ 9 Queue q0,q1, q2, q3, q4, q5, q6, q7, q8, q9; //获取该数据第几位的数字 int GetKey(int val, int k) { int keyi = 0; while (k >= 0) { keyi = val % 10; val /= 10; k--; } return keyi; } //分发数据 void Distribute(int* a, int left, int right, int k) { for (int i = left; i < right; i++) { //获取当前要排序的位上的数据。 int key = GetKey(a[i], k); //按照数据的每个位上的数字,分别进入对应的队列 switch (key) { case 0: QueuePush(&q0, a[i]); break; case 1: QueuePush(&q1, a[i]); break; case 2: QueuePush(&q2, a[i]); break; case 3: QueuePush(&q3, a[i]); break; case 4: QueuePush(&q4, a[i]); break; case 5: QueuePush(&q5, a[i]); break; case 6: QueuePush(&q6, a[i]); break; case 7: QueuePush(&q7, a[i]); break; case 8: QueuePush(&q8, a[i]); break; case 9: QueuePush(&q9, a[i]); break; default: break; } } } //回收数据 void Collect(int* a) { //下标值 int i = 0; //依次取出0到9队列中的数据 while (!QueueEmpty(&q0)) { a[i++] = QueueFront(&q0); QueuePop(&q0); } while (!QueueEmpty(&q1)) { a[i++] = QueueFront(&q1); QueuePop(&q1); } while (!QueueEmpty(&q2)) { a[i++] = QueueFront(&q2); QueuePop(&q2); } while (!QueueEmpty(&q3)) { a[i++] = QueueFront(&q3); QueuePop(&q3); } while (!QueueEmpty(&q4)) { a[i++] = QueueFront(&q4); QueuePop(&q4); } while (!QueueEmpty(&q5)) { a[i++] = QueueFront(&q5); QueuePop(&q5); } while (!QueueEmpty(&q6)) { a[i++] = QueueFront(&q6); QueuePop(&q6); } while (!QueueEmpty(&q7)) { a[i++] = QueueFront(&q7); QueuePop(&q7); } while (!QueueEmpty(&q8)) { a[i++] = QueueFront(&q8); QueuePop(&q8); } while (!QueueEmpty(&q9)) { a[i++] = QueueFront(&q9); QueuePop(&q9); } } void RadixSort(int* a, int left, int right) { //初始化队列 QueueInit(&q0); QueueInit(&q1); QueueInit(&q2); QueueInit(&q3); QueueInit(&q4); QueueInit(&q5); QueueInit(&q6); QueueInit(&q7); QueueInit(&q8); QueueInit(&q9); for (int i = 0; i < K; i++) { //分发数据 Distribute(a, left, right, i); //回收数据 Collect(a); } //销毁队列 QueueDestroy(&q0); QueueDestroy(&q1); QueueDestroy(&q2); QueueDestroy(&q3); QueueDestroy(&q4); QueueDestroy(&q5); QueueDestroy(&q6); QueueDestroy(&q7); QueueDestroy(&q8); QueueDestroy(&q9); }因为我们使用纯C来写的,所以在一些代码上比较麻烦,需要注意一下几点:
1 . 队列要定义为全局的,方便我们直接使用,否则作为参数传递太过麻烦。
2. 我们可以直接写入要排的数据的最大位数,也可以写入的位数大一点,比如最大值只有百位的数据,我们可以写入千位,也就是比预定的要多排序一次,只会影响效率,不会影响结果。
3.使用队列的好处是我们不用考虑数据先进先出这点啦,因为这是队列的性质。
4.我们需要先写好一个队列才能使用上面的方法。
??
上述的写法十分麻烦,下面我们使用数组方式实现。
代码实现(数组实现):
//求数据的最大值 int GetMaxBitCount(int* array, int size) { //设定位数初始值 int max_count = 1; //设定初始边界值 int bound = 10; // 针对数组中的每一个元素, 都使用边界值来进行试探. // 看看边界值是否能够涵盖数组中的当前值. int i = 0; for (; i < size; ++i) { while (array[i] >= bound) { ++max_count; bound *= 10; } } //返回数据中最大的位数 return max_count; } void RadixSort1(int* array, int size) { // 1. 求出最大的数字是多少位 int max_bit_count = GetMaxBitCount(array, size); //开辟临时数组 int* bucket = (int*)malloc(sizeof(int)* size); // 2. 最大的数字有多少位, 就需要进行多少次的排序 int radix = 1; // 表示当前要取个位, 十位, 还是百位... int count = 0; for (; count < max_bit_count; ++count, radix *= 10) { // 统计每个桶中的元素个数(基数桶) int bucket_count[10] = { 0 }; int i = 0; for (; i < size; ++i) { ++bucket_count[array[i] / radix % 10]; } // 根据每个桶的元素的个数, 分配起始位置.(辅助数组) // 一维数组表示二维数组 int start_addr[10] = { 0 }; for (i = 1; i < 10; ++i) { start_addr[i] = start_addr[i - 1] + bucket_count[i - 1]; } // 代码运行到这里, 就已经把地盘瓜分好了. // 接下来将所有的元素放到桶中 for (i = 0; i < size; ++i) { int bucket_no = array[i] / radix % 10; // 这里的 start_addr[bucket_no]++ 相当于线性表的尾插. // 通过 start_addr[bucket_no] 记录每个桶当前写到了哪个位置. bucket[start_addr[bucket_no]++] = array[i]; } memcpy(array, bucket, sizeof(int)* size); } }使用数组方式更为简洁,但是理解上更为麻烦些:
1.我们先试探边界求出最大数的位数。
2.在根据每次个位或者十位等等,这些位上的数据放入一个基数桶中。
3.最后我们要按照0~9这样的顺序插入到临时数组中
4.在插入时我们要根据辅助数组的顺序依次插入,这个类似一维数组表示二维数组的形式。
5.最后拷贝回原数组,释放空间。
今天到这里就结束啦!?