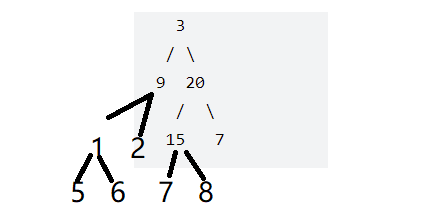文章目录
🍈栈的压入、弹出序列
剑指 Offer 31. 栈的压入、弹出序列 - 力扣(LeetCode)
借助一个辅助栈模拟即可。
class Solution {
public:
bool validateStackSequences(vector<int>& pushed, vector<int>& popped) {
int push_sz = pushed.size();
int pop_sz = popped.size();
if (push_sz == 0&&pop_sz==0)
{
return true;
}
stack<int>push_st;
push_st.push(pushed[0]);
int j = 0;
for (int i = 1; i < pushed.size(); i++)
{
if (!push_st.empty()&&push_st.top() == popped[j])
{
while (!push_st.empty() && push_st.top() == popped[j])
{
push_st.pop();
j++;
}
}
push_st.push(pushed[i]);
}
while (!push_st.empty() && push_st.top() == popped[j])
{
push_st.pop();
j++;
}
if (push_st.empty())
{
return true;
}
return false;
}
};
根据大佬的题解简化了一下。这是代码实现的角度,时间复杂度上并没什么不同。
优化的点在于:代码实现上我先把第一个元素入栈,再去比较栈顶元素和pop序列,之后再将push序列的元素入栈。代码可以优化为,每次判断前先把元素入栈再去判断,就不用在循环结束再用一个while循环去比较。
class Solution {
public:
bool validateStackSequences(vector<int>& pushed, vector<int>& popped) {
int push_sz = pushed.size();
if (push_sz == 0)
{
return true;
}
stack<int>push_st;
int j = 0;
for (int i = 0; i < push_sz ; i++)
{
push_st.push(pushed[i]);
if (!push_st.empty()&&push_st.top() == popped[j])
{
while (!push_st.empty() && push_st.top() == popped[j])
{
push_st.pop();
j++;
}
}
}
return push_st.empty();
}
};
🍈从上到下打印二叉树
剑指 Offer 32 - I. 从上到下打印二叉树 - 力扣(LeetCode)
层序遍历二叉树,也就是我们说的BFS,常用队列实现。
第一种写法,队列里有空指针。
class Solution {
public:
vector<int> levelOrder(TreeNode* root) {
queue<TreeNode*>q;
q.push(root);
vector<int>ret;
while (!q.empty())
{
TreeNode* tmp = q.front();
q.pop();
if (tmp)
{
ret.push_back(tmp->val);
q.push(tmp->left);
q.push(tmp->right);
}
}
return ret;
}
};
第二个版本,队列里始终没有空指针。
class Solution {
public:
vector<int> levelOrder(TreeNode* root) {
queue<TreeNode*>q;
vector<int>ret;
if(root==NULL)
{
return ret;
}
q.push(root);
while (!q.empty())
{
TreeNode* tmp = q.front();
q.pop();
ret.push_back(tmp->val);
if (tmp->left)
{
q.push(tmp->left);
}
if (tmp->right)
{
q.push(tmp->right);
}
}
return ret;
}
};
🍊拓展
🥝从上到下打印二叉树 II
剑指 Offer 32 - II. 从上到下打印二叉树 II - 力扣(LeetCode)
分行打印每一层的结点的值。这就得用到是上面层序遍历的第二种写法,保证空节点不入队,这样就能获取每一层的节点数。拿到结点数再借助循环挨个出队,再将自己的孩子节点入队即可。
代码实现上要记得队列不止有push和pop方法,还有size()方法
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> ret;
if (root==NULL)
{
return ret;
}
queue<TreeNode*>q;
q.push(root);
while (!q.empty())
{
vector<int>tmp;
int sz = q.size();
for (int i=0;i<sz;i++)//每次都把这一层的出队
{
TreeNode* t = q.front();
tmp.push_back(t->val);
q.pop();
if (t->left) q.push(t->left);
if (t->right) q.push(t->right);
}
ret.push_back(tmp);
}
return ret;
}
};
🥝从上到下打印二叉树 III
剑指 Offer 32 - III. 从上到下打印二叉树 III - 力扣(LeetCode)
🍒控制入队和出队方式
这种写法真的绕(后面会给一种简化点的思想),思想是利用双端队列可头插可尾插。
奇数行:从头取到尾(好让下一层的孩子入队),左孩子尾插入队,再右孩子尾插入队,保证左孩子在右孩子的后面,自己的值尾插到存放结果的数组里面。
偶数行:从尾取到头(好让下一层的孩子入队),右孩子头插入队,再左孩子头插入队,保证右孩子在左孩子的后面,自己的值尾插到存放结果的数组里面。
3先入队,队列里的数是奇数行(第一行)的,左孩子9入队,再20入队。到了9和20这一层,从尾遍历到头,把20的右孩子7入队,再把15,2,1分别头插入队,第三层时队列里的元素就是1,2,15,7,再从头遍历到尾,从1开始,1的左孩子5尾插入队,…到第四层时队列里的元素为5,6,7,8;再从尾遍历到头。
利用头插入队和尾插入队使得队列里每一层的元素与图中元素从左到右排列的序列相同,只不过对于奇偶层的遍历方式不同,而遍历序列就是我们要的结果。说了这么多,看代码自己模拟一遍最清楚(是真的绕)。
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>>ret;
if (root == NULL)
{
return ret;
}
deque<TreeNode*>q;
q.push_back(root);
int cnt = 1;
while (!q.empty())
{
int sz = q.size();
vector<int>tt;
if (cnt%2==1)//奇数
{
for (int i = 0; i < sz; i++)
{
TreeNode* tmp = q.front();
tt.push_back(tmp->val);
q.pop_front();
if (tmp->left)
{
q.push_back(tmp->left);
}
if (tmp->right)
{
q.push_back(tmp->right);
}
}
}
else//偶数
{
for (int i = 0; i < sz; i++)
{
TreeNode* tmp = q.back();
tt.push_back(tmp->val);
q.pop_back();
if (tmp->right)
{
q.push_front(tmp->right);
}
if (tmp->left)
{
q.push_front(tmp->left);
}
}
}
ret.push_back(tt);
cnt++;
}
return ret;
}
};
🍒控制出队元素存入结果数组的方式
上面的写法那么绕,参考题解区有一种简单点的思路。
保证队列里每一层的序列和树每一层从左到右的序列相同,也就是最开始讲的队列里没有空指针的层序遍历。之后对于每一层,奇数层就尾插,偶数层就尾插。
保证队列里放的每一层数据是[3] [9,20] [1,2,15,7] [5,6,7,8]
对于奇数层尾插,比如1,2,15,7尾插后还是1,2,15,7
对于偶数层头插,比如5,6,7,8头插后就是8,7,6,5;就是我们要的遍历结果
简单来说,确定队列里元素的排列,再改变每一层放入数组的方式即可。(抽象就自己模拟一遍吧)
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>>ret;
if (root == NULL)
{
return ret;
}
queue<TreeNode*>q;
q.push(root);
int cnt = 1;
while (!q.empty())
{
int sz = q.size();
vector<int>tmp;
if (cnt % 2 == 1)
{
for (int i = 0; i < sz; i++)
{
TreeNode* cur = q.front();
tmp.push_back(cur->val);
q.pop();
if (cur->left)
{
q.push(cur->left);
}
if (cur->right)
{
q.push(cur->right);
}
}
}
else
{
for (int i = 0; i < sz; i++)
{
TreeNode* cur = q.front();
tmp.insert(tmp.begin(),cur->val);
q.pop();
if (cur->left)
{
q.push(cur->left);
}
if (cur->right)
{
q.push(cur->right);
}
}
}
ret.push_back(tmp);
cnt++;
}
return ret;
}
};
第三种办法,把每次读到的一层,奇数行不变,偶数行翻转,这种办法也可以。但是有点取巧的意思了。
🍈二叉搜索树的后序遍历序列
剑指 Offer 33. 二叉搜索树的后序遍历序列 - 力扣(LeetCode)
分区间进行判断左子树是否小于根,右子树是否都大于根,递归检查所有子树符不符合这个性质,符合就是二叉搜索树,,否则就不是。
注意区间边界,每检查一次,根节点肯定被剔除了然后进行下一轮检查,因为检查的就是以这个结点为根结点的树是不是二叉搜索树。
参考题解区大佬才实现的代码,下次判断左右子树性质时可以想想分区间+递归判断
class Solution {
public:
bool Check(vector<int>& postorder,int left, int right)//left和right都可以取到
{
if (left >= right)
{
return true;//只有一个结点,或者没有结点,检查到叶子了。
}
int p = left;//postorder[right]就是这个序列的根
while (postorder[p]<postorder[right])
{
p++;
}
int mid = p;//此时p的左边就是左子树
while (postorder[p]>postorder[right])
{
p++;
}
//如果左子树都小于根,右子树都大于根,此时的p就会停在right这个位置
//所以我们只要检查p是不是在right的位置,就可以知道当前树满不满足二叉搜索树的性质
//再进行递归检查每一颗子树,就能知道整棵树是不是二叉搜索树
return p == right && Check(postorder,left, mid - 1) && Check(postorder,mid, right-1);
}
bool verifyPostorder(vector<int>& postorder) {
return Check(postorder,0, postorder.size() - 1);
}
};
单调栈(栈里的元素是单调的)法,时间复杂度是O(n)
我想不到。。。参考题解区的K神代码实现了一下,只能知道这么做可以,不知道为啥可以这么做
单调栈的思路:后序倒过来,变成根右左,此时从前往后遍历肯定是先升序再降序,因为右子树的每个结点都大于根。
当碰到降序的结点时,可以发现这个结点的父亲一定在栈里面,而且是栈里最接近他的,即栈里大于他但是差值最小的就是他的根节点。通过这种方法可以发现,当我们能成功遍历完,即所有的结点都符合二叉搜索树的性质,那整棵树都是二叉搜索树。
[例子理解](https://leetcode.cn/problems/er-cha-sou-suo-shu-de-hou-xu-bian-li-xu-lie-lcof/solution/di-gui-he-zhan-liang-chong-fang-shi-jie-jue-zui-ha/
class Solution {
public:
bool verifyPostorder(vector<int>& postorder) {
stack<int>st;
int root = 0x7fffffff;//INT_MAX
for (int i=postorder.size()-1;i>=0;i--)
{
if (postorder[i]>root)//有一个结点不符合搜索树的性质直接return false
{
return false;
}
while (!st.empty() && st.top() > postorder[i])//把根节点以及大于根节点的数据全部pop,因为栈是单调的
{
root =st.top();
st.pop();
}
st.push(postorder[i]);
}
return true;
}
};
🍈二叉树中和为某一值的路径
剑指 Offer 34. 二叉树中和为某一值的路径 - 力扣(LeetCode)
回溯法记录路径,但是注意找到路径不能立即退出,走到叶子之后不管找没找到都要把结点删掉(pop_back),这样才能不影响回溯,不然可能造成多了几个结点的情况。
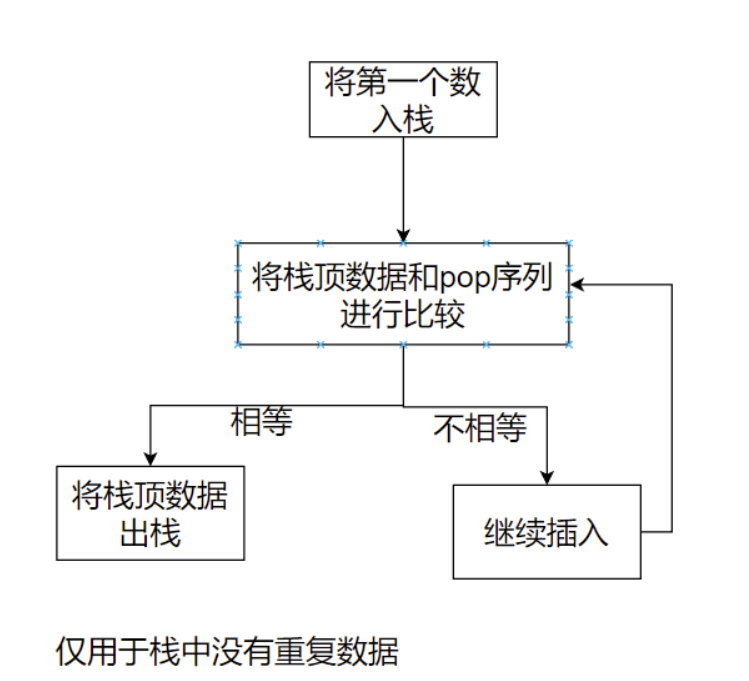
书上给的总结
利用vector保存栈的路径
class Solution {
public:
void PreOrder(TreeNode* root,int k, int target)
{
if(root==NULL)//处理传进来为空的结点
{
return ;
}
k+=root->val;
path.push_back(root->val);//当前结点尾插进去
if (root->left==NULL&&root->right==NULL&&k==target)
{
ret.push_back(path);//找到叶子就是一条路径 这条路径合理,不能立即return
}
PreOrder(root->left, k,target);
PreOrder(root->right, k,target);
path.pop_back();//回溯
return ;
}
vector<vector<int>> pathSum(TreeNode* root, int target) {
if(root==NULL)
{
return ret;
}
PreOrder(root, 0, target);
return ret;
}
private:
vector<int>path;
vector<vector<int>>ret;
};
🍈复杂链表的复制
剑指 Offer 35. 复杂链表的复制 - 力扣(LeetCode)
🍊哈希
哈希思想有两版代码,第一版是我自己写的,写的很垃圾。代码细节(就没有细节),建议直接跳到第二版,第一版的代码仅为记录。
我搞了三个映射关系
(旧链表的结点地址,新链表的结点地址)
(旧链表的结点地址,旧结点的random结点地址)
(新链表的结点地址,旧链表的结点地址)
这三个映射关系都是为了random结点服务的。
我的思想是有一个新节点。找到新节点的random结点的顺序:新节点->新节点对应的旧结点->旧结点对应的旧random结点->旧random结点对应的新节点。前后分别用到了新老地址的映射,旧和旧random地址的映射,旧地址和新地址的映射。
class Solution {
public:
Node* copyRandomList(Node* head) {
if(head==NULL)
{
return NULL;
}
Node* cur =head;
Node* phead= new Node(head->val);//新链表的第一个头结点
map<Node*, Node*>m_on;
map<Node*, Node*>m_or;
map<Node*, Node*>m_no;
m_on[head] = phead;//新地址-》旧地址-》旧结点random的地址-》新节点的地址
m_no[phead] = head;
m_or[head] = head->random;
cur = cur->next;
Node* pcur=phead;//负责新链表next的链接
while (cur!=NULL)
{
Node* tmp=new Node(cur->val);//拷贝一个cur结点
pcur->next = tmp;//把这个结点新的结点连起来
m_on[cur] = tmp;
m_no[tmp] = cur;
m_or[cur] = cur->random;
cur = cur->next;
pcur=pcur->next;
}
cur = phead;//遍历新链表
while (cur)
{
cur->random = m_on[m_or[m_no[cur]]];
cur = cur->next;
}
return phead;
}
};
第二种哈希解法
看了K神的映射思路,只需要一个映射关系:(旧地址,新地址)
然后第一次遍历链表建立旧地址和新地址的关系,之后再根据map[cur]->next = map[cur->next];这种思想就能构建出整个链表。
class Solution {
public:
Node* copyRandomList(Node* head) {
unordered_map<Node*, Node*>map;
Node* cur = head;
while (cur)
{
Node* tmp = new Node(cur->val);
map[cur] = tmp;//新老地址映射
cur = cur->next;
}
cur = head;
while (cur)
{
map[cur]->next = map[cur->next];
map[cur]->random = map[cur->random];
cur=cur->next;
}
return map[head];
}
};
🍊构建拆分链表
构建出一个链表,每个旧结点后面都跟他自己的拷贝,也就是新节点,这样new_node->random和old_node->random->next就对应起来了。题解区有大佬画图
构成的这个链表里面有一部分是新链表,所以再把这个链表拆分就能得到新链表。
代码实现上注意空指针的引用,要熟悉对链表的操作,最重要的是分治法的思想。每一步必须清楚要做什么,比如构建新链表的random指针得单独用一个循环,而不能一边循环构建random指针一边去拆分链表,我一开始是这么做的,然后一直报错…解决了空指针结果也不对,后面看到题解区大佬的代码才发现拆分链表和构建random指针不能同时进行。题目隐含的要求是将旧的链表还原。
class Solution {
public:
Node* copyRandomList(Node* head) {
if (head==NULL)
{
return NULL;
}
Node* cur = head;
//构建链表
while (cur)
{
Node* tmp = new Node(cur->val);
Node* next = cur->next;
cur->next = tmp;
tmp->next = next;
cur = next;
}
//构建random指针
cur = head;
while(cur)
{
if(cur->random)
{
cur->next->random=cur->random->next;
}
else
{
cur->random=NULL;
}
cur=cur->next->next;
}
//拆分链表
cur=head->next;
Node* prev=head;
Node* newhead=cur;
while(cur)
{
prev->next=prev->next->next;
if(cur->next)
{
cur->next=cur->next->next;
}
else{
cur->next=NULL;
}
prev=prev->next;
cur=cur->next;
}
return newhead;
}
};