问题:给定一个不含重复数字的数组?nums?,返回其?所有可能的全排列?。你可以?按任意顺序?返回答案。
输入:nums = [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
回溯法
? ? ? ? 回溯算法其实是一种穷举的搜索方法,利用回溯解决问题就是在穷举所有的可能,然后找到我们想要的答案。使用回溯算法时需要考虑如下的三个问题:
????(1) 可选列表:所有可作出的选择;
????(2) 已选列表:也就是之前已经做出的选择;
????(3) 结束条件:当已选列表满足题目条件,可以结束穷举;
python 回溯算法框架
def backtrack(选择列表,路径):
if 终止条件:
存放结果
return
for 选择 in 选择列表(本层集合中元素):
处理节点
backtrack(选择列表,路径)
回溯,撤销处理结果生成全排列算法1:
? ? ? ? 我们可以将题目给定的 n 个数的数组 nums 划分成左右两个部分,左边的表示已经填过的数,右边表示待填的数,我们在回溯的时候只要动态维护这个数组即可。
? ? ? ? 具体来说,假设我们已经填到第 first 个位置,那么 nums 数组中 [0,first ? 1] 是已填过的数的集合,[first , n - 1] 是待填的数的集合。我们肯定是尝试用 [first , n - 1]里的数去填第 first 个数,假设待填的数的下标为 i,那么填完以后我们将第 i?个数和第 first 个数交换,即能使得在填第 first + 1 个数的时候 nums 数组的 [0 , first] 部分为已填过的数,[first + 1,n ? 1] 为待填的数,回溯的时候交换回来即能完成撤销操作。
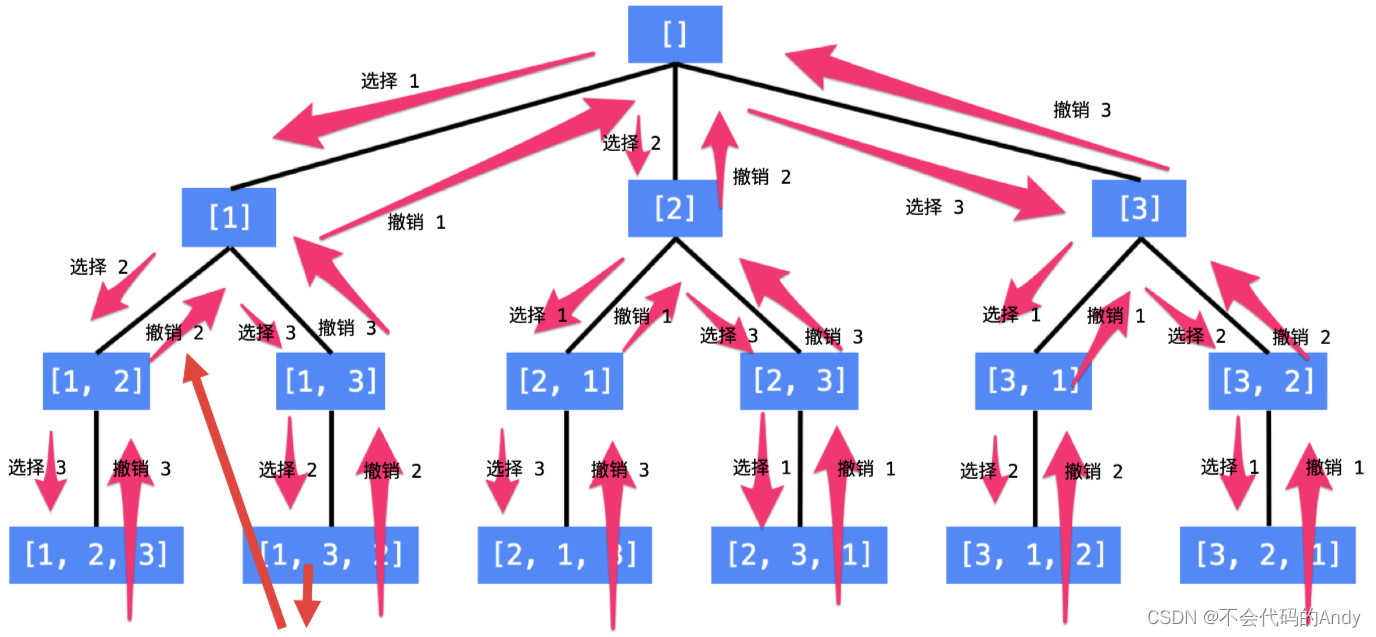
? ? ? ? 如图,每个树状节点是已填过的数(个数为first+1个)的集合,而该节点的子节点则是将待填的数的集合通过两个数元素的交换来填写第 first 个数。如[1,2,3,4],假设已经填到了第3个位置,[2,4]已填入,则该节点目前状态为[2,4 | 1,3]。假设需要填入3这个元素,我们则对1和3进行交换,first指针右移一位,变成[2,4,3 | 1]状态。
import copy
from typing import List
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
def backtrack(n: int, nums: [int], res: List[List[int]], first: int):
if first == n:
c = copy.copy(nums)
res.append(c) # 需要深拷贝
for i in range(first, n):
nums[i], nums[first] = nums[first], nums[i]
backtrack(n, nums, res, first + 1)
nums[i], nums[first] = nums[first], nums[i]
res = []
backtrack(len(nums), nums, res, 0)
return res
s = Solution()
print(s.permute([1, 2, 3]))
注意:其中res.append(c)需要用深拷贝,将nums当前的值赋给c,不然res.append存储的是nums的指针,最后res队列的若干结果都会相同。
生成全排列算法2:
排列问题与算法1不同:
? ? ? ? 1、每层都是从0开始搜索而不是first;
? ? ? ? 2、需要对新元素是否在path数组里做判断;
from typing import List
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
res = [] # 存放符合条件结果的集合
path = [] # 用来存放符合条件的结果
def backtrack(nums):
if len(path) == len(nums):
return res.append(path[:]) # 此时说明找到了一组,此处为深拷贝
for i in range(0, len(nums)):
if nums[i] in path: # path里已经收录的元素,直接跳过
continue
path.append(nums[i])
backtrack(nums) # 递归
path.pop() # 回溯
backtrack(nums)
return res
s = Solution()
print(s.permute([1, 2, 3]))注意:res.append(path[:]) 此处为深拷贝,若改成res.append(path),则结果为 [[], [], [], [], [], []] ,因为此时res中均为指向path的指针,而path中的值全部被pop。