排序
一、 排序的基本概念
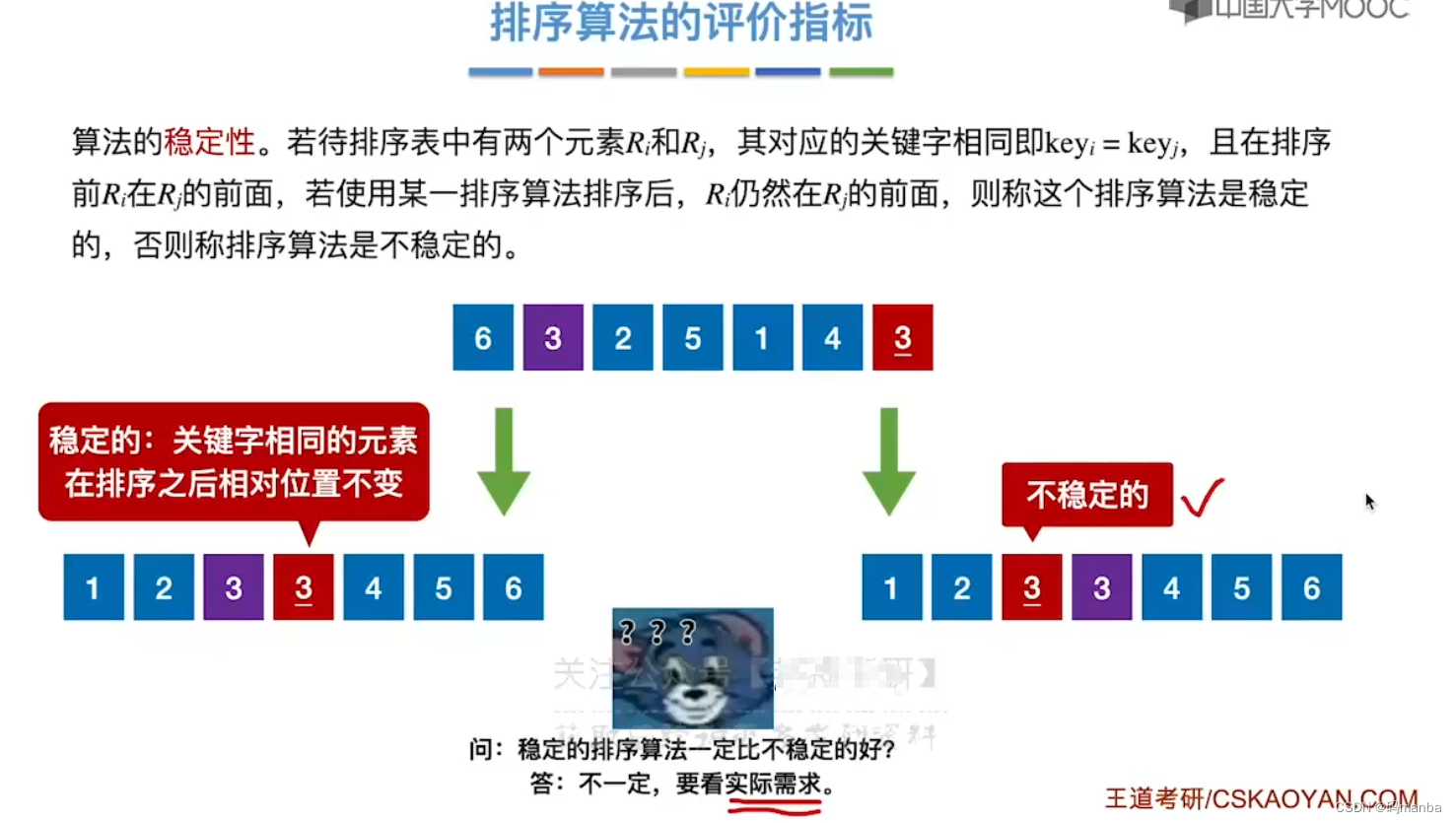
1.1 排序算法的评价指标
- 稳定性
- 注意并不一定一定要求稳定,但是如果排序的字段其他信息不一致,就要要求稳定性了。
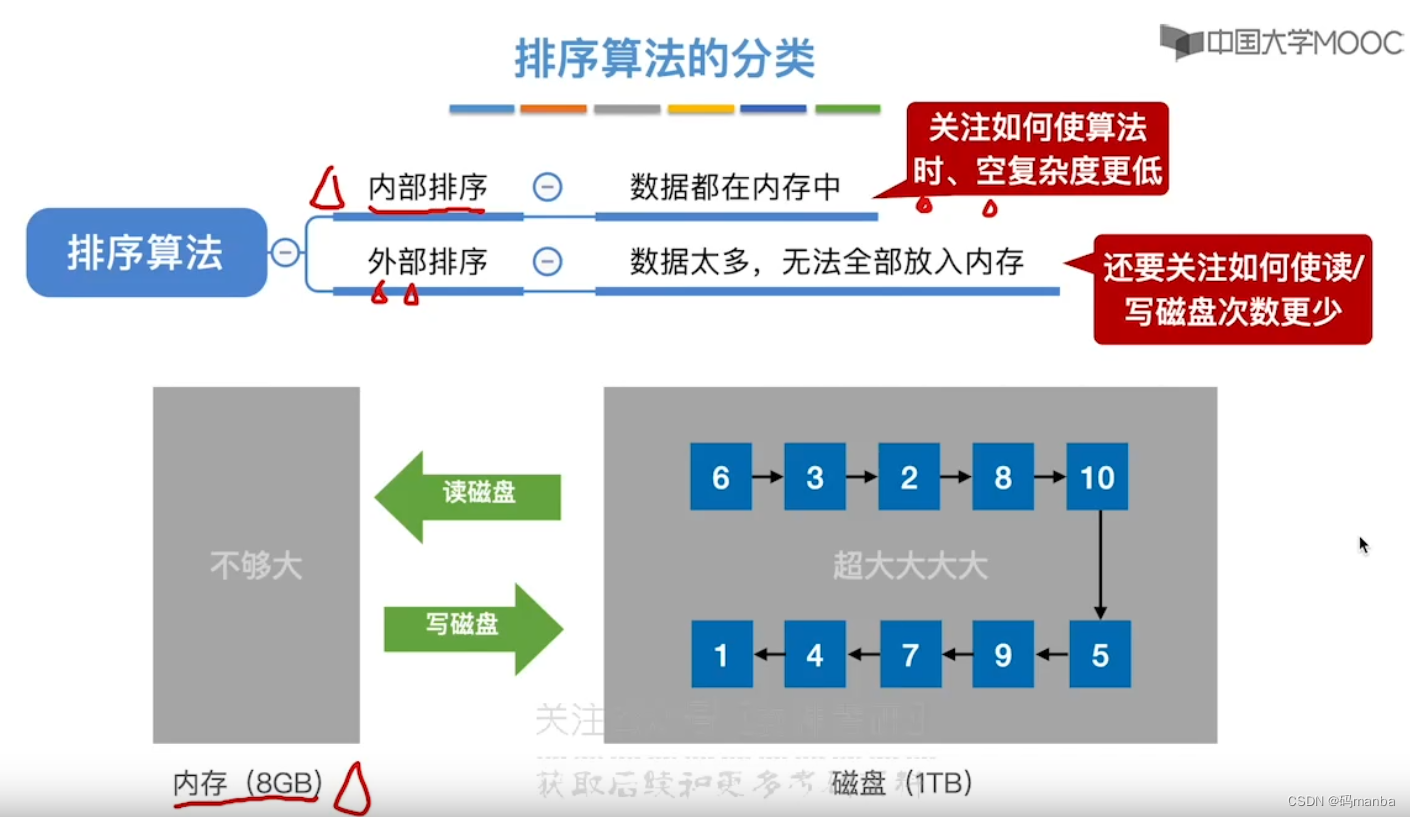
1.2 内部 排序和外部排序
- 内部排序: 数据都在内存,关注 时间复杂度、空间复杂度
- 外部排序: 数据也在外村,关注 时间复杂度、空间复杂度、磁盘读写次数
二、 插入排序
2.1 直接插入排序
存储结构: 顺序存储、链式存储;
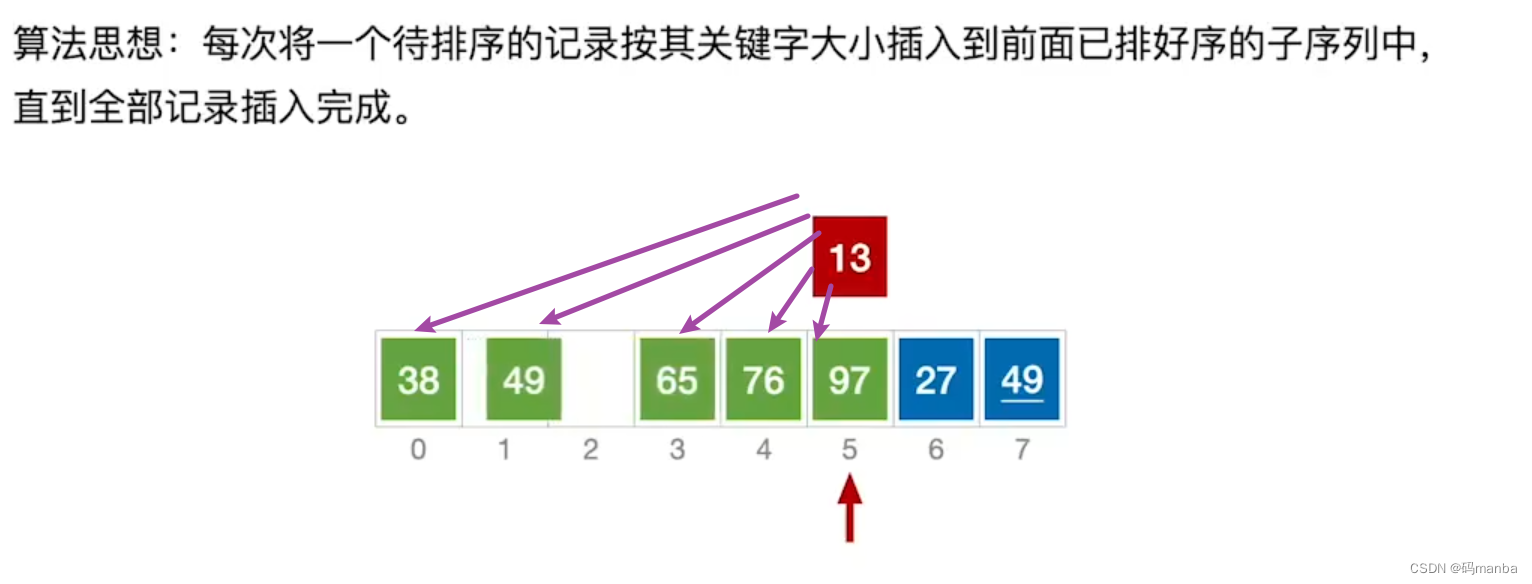
直接插入排序的算法思想
- 以 从小到大排序为例;
- 最开始从下标为1的元素开始, for(1 -> n-1)
- 先保存当前元素;当前元素与前驱元素进行比较。 当小于前驱元素时, 前驱元素后移;
- 后移后当前元素依次与前面所有元素进行比较, 大的后移一次;直到不再比当前元素大,将当前元素放到最终位置;
算法实现
- 非哨兵实现方式

- 哨兵实现方式

算法效率分析
? 空间复杂度

? 时间复杂度
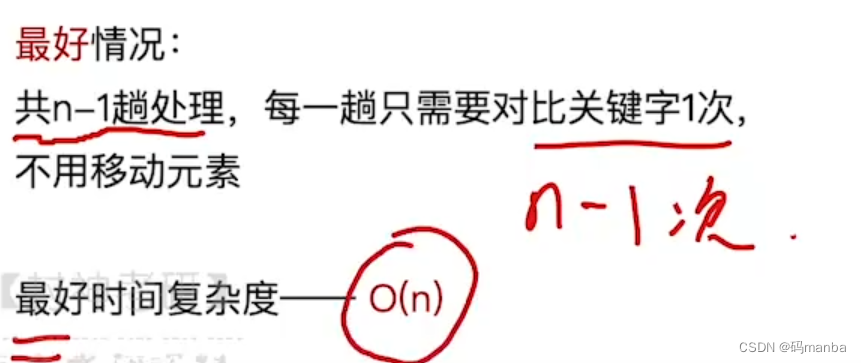
- 最好情况
就是本来就是排好序的,只进行 n-1次比较;
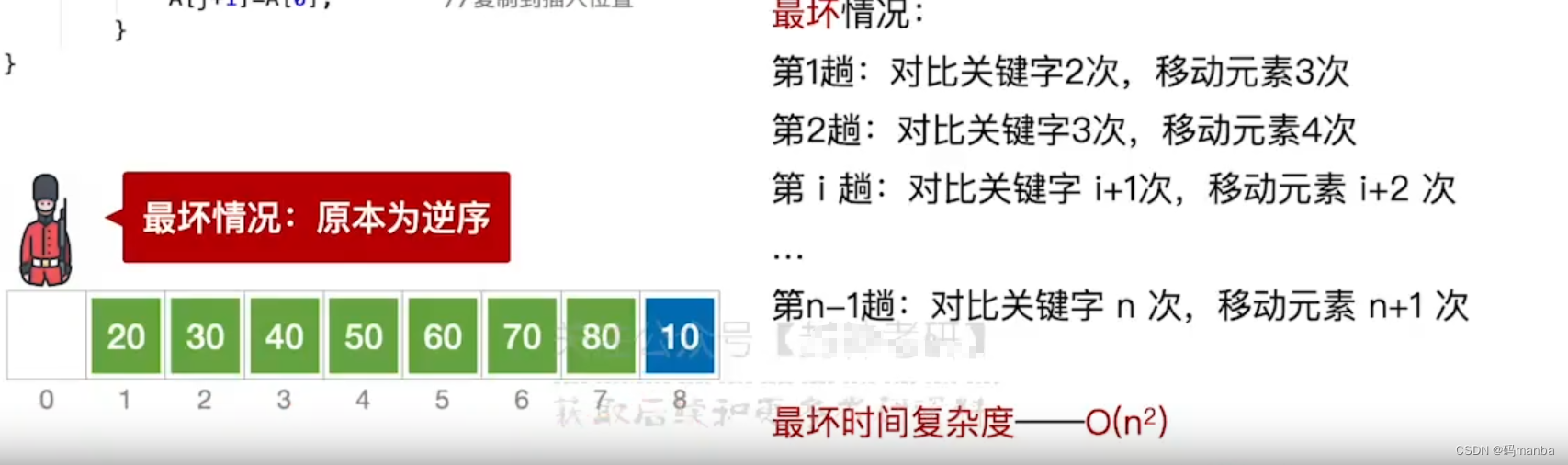
2. 最差情况
每次对比都进行n+1次移动;
? 算法分析总结

采用链式存储结构
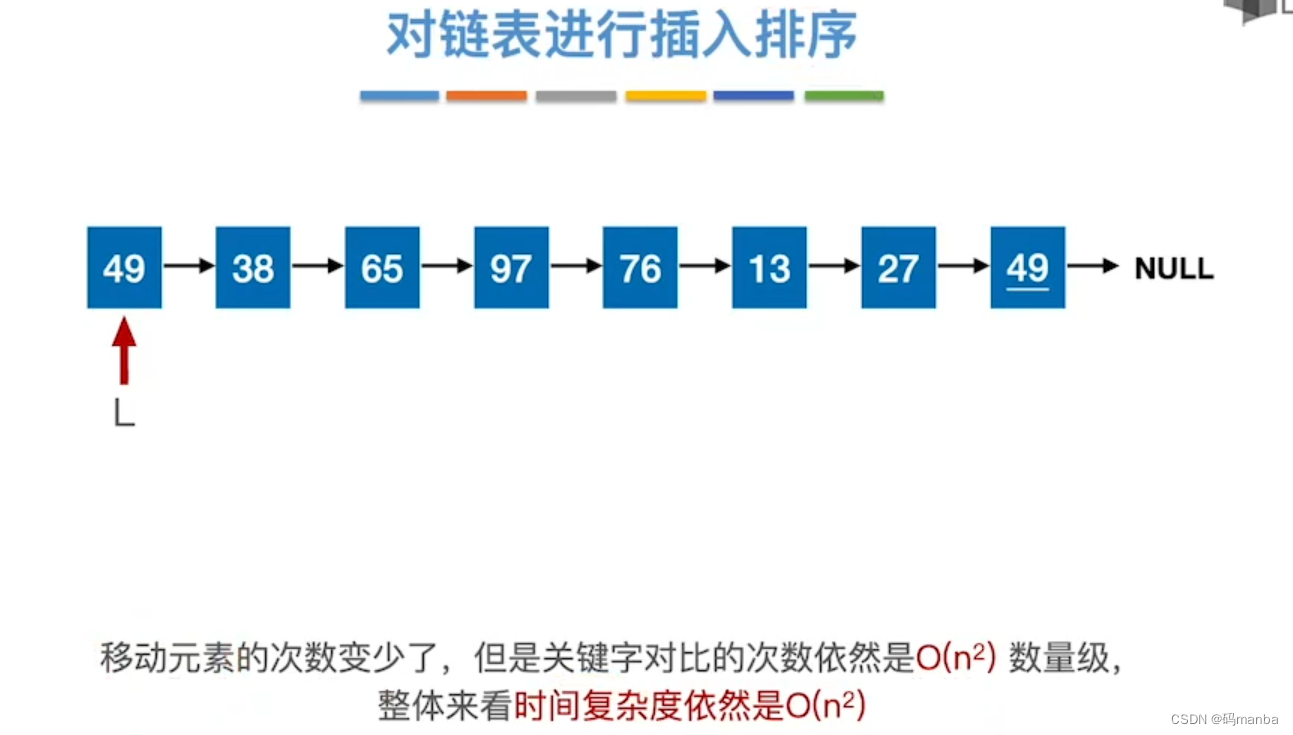
2.2 折半插入排序
存储结构 : 顺序结构
链式存储结构实现不了(因为折半查找的原因)
算法思想
- 由于前面的序列已经有序,所以
- 先通过折半查找找 当前元素要插入到前遍序列的位置, 再将该位置后的元素依次后移,将当前元素插入到指定位置;
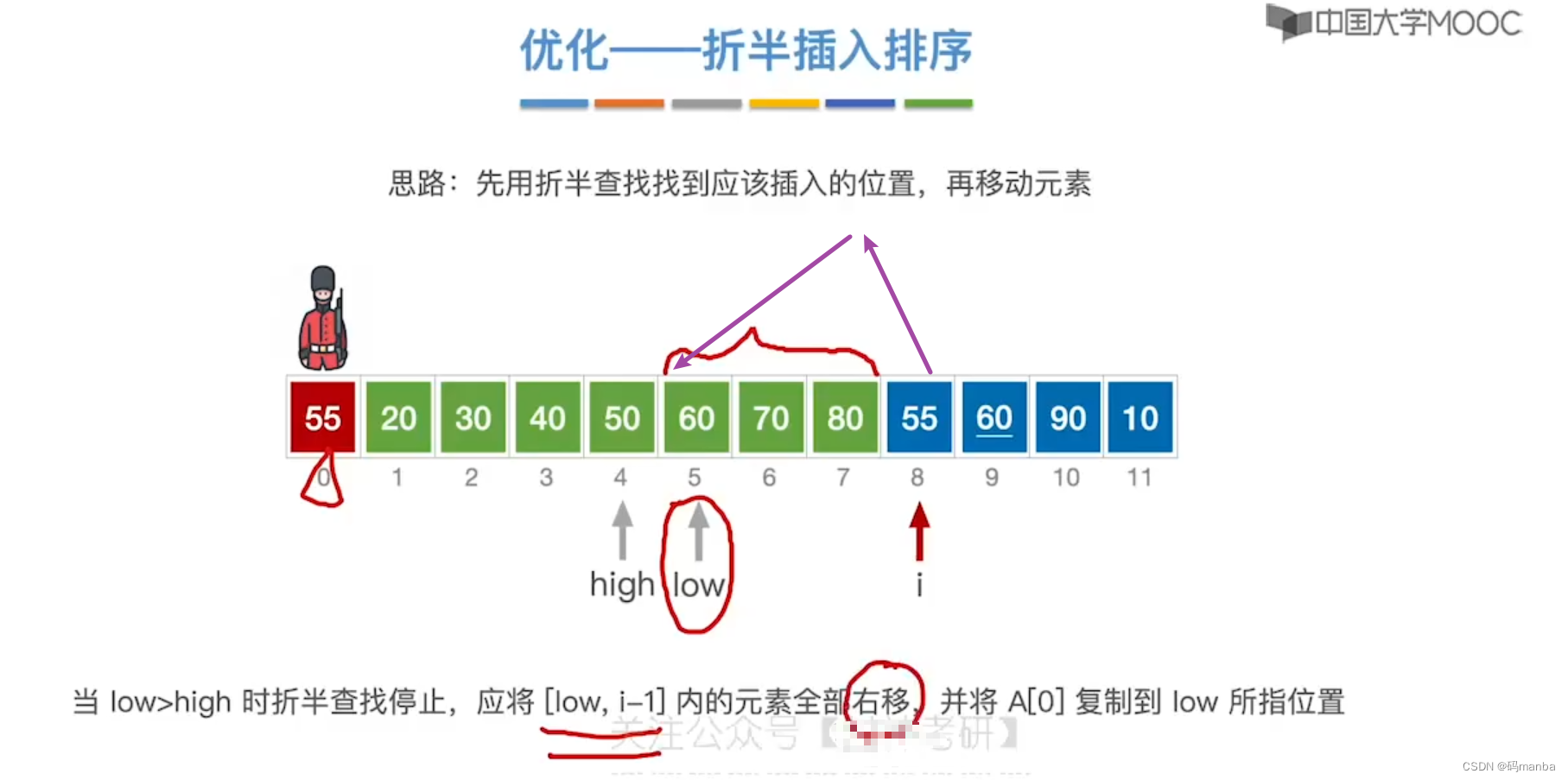
折半插入代码
- 哨兵实现方式

效率分析

2.3 插入排序和折半插入排序知识总结
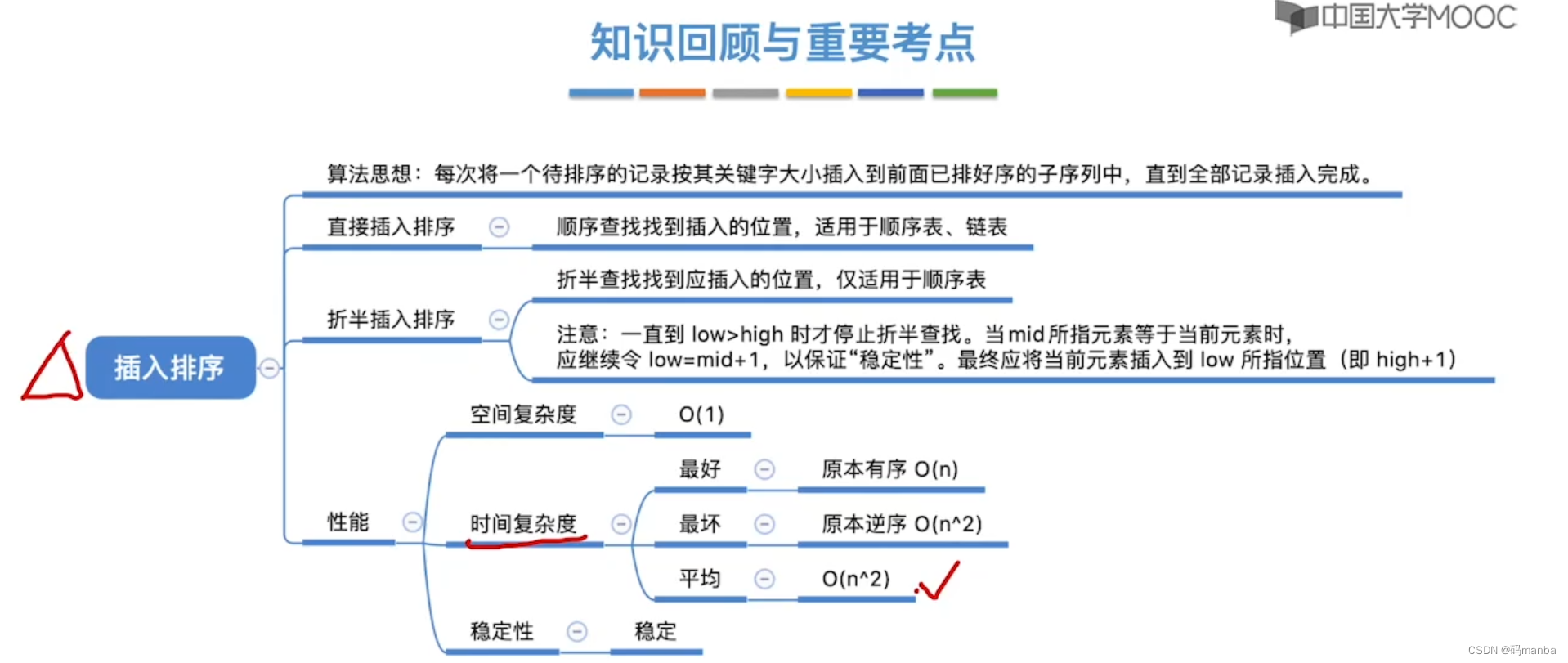
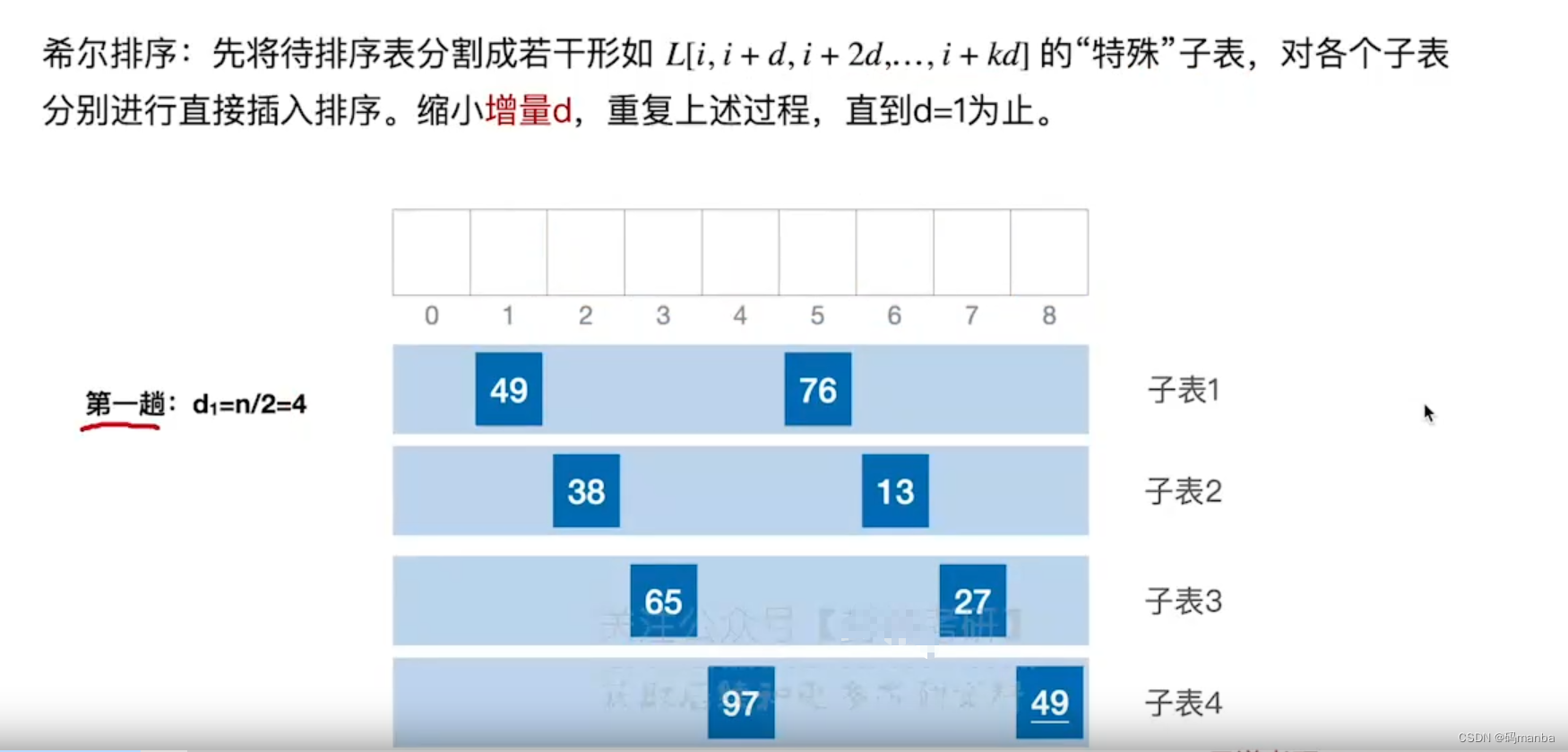
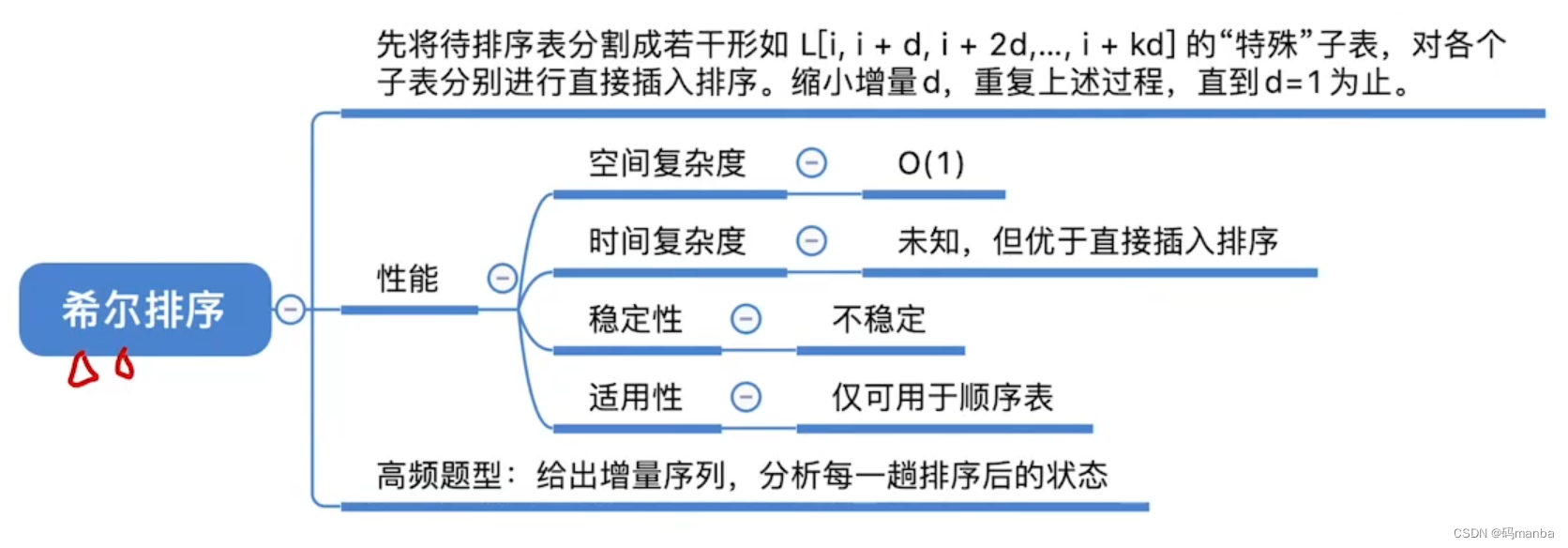
2.4 希尔排序

希尔排序介绍
- 第一趟 (d增量设为 4; ?即n(元素个数) / 2)
? 排序前 (划分成多个子表, 按增量d划分, 例如 1+d,1+2d,1+3d为一个子表)
? 排序后 (就是子表内 进行 直接插入排序)
- 第二趟 (d=4/2 = 2)
? 排序前
? 排序后
- 第三趟 (d= 4/2/2 = 1)
? 排序前
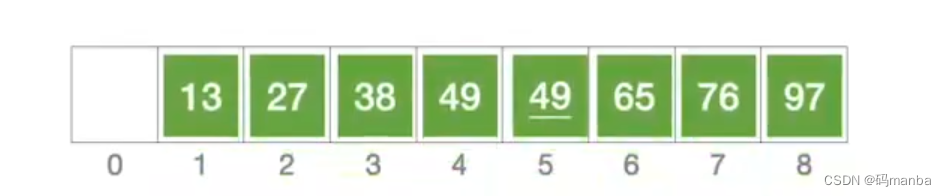
? 排序后
? 总览

算法实现
- 代码描述图片已经标记
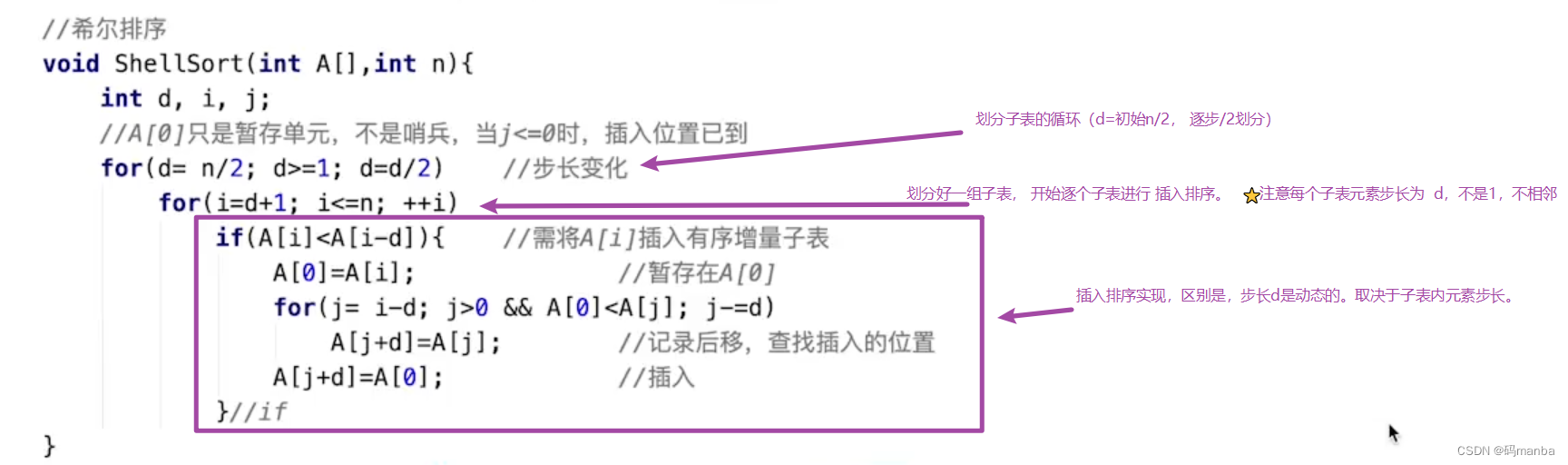
算法性能分析
- 时间复杂度和空间复杂度分析
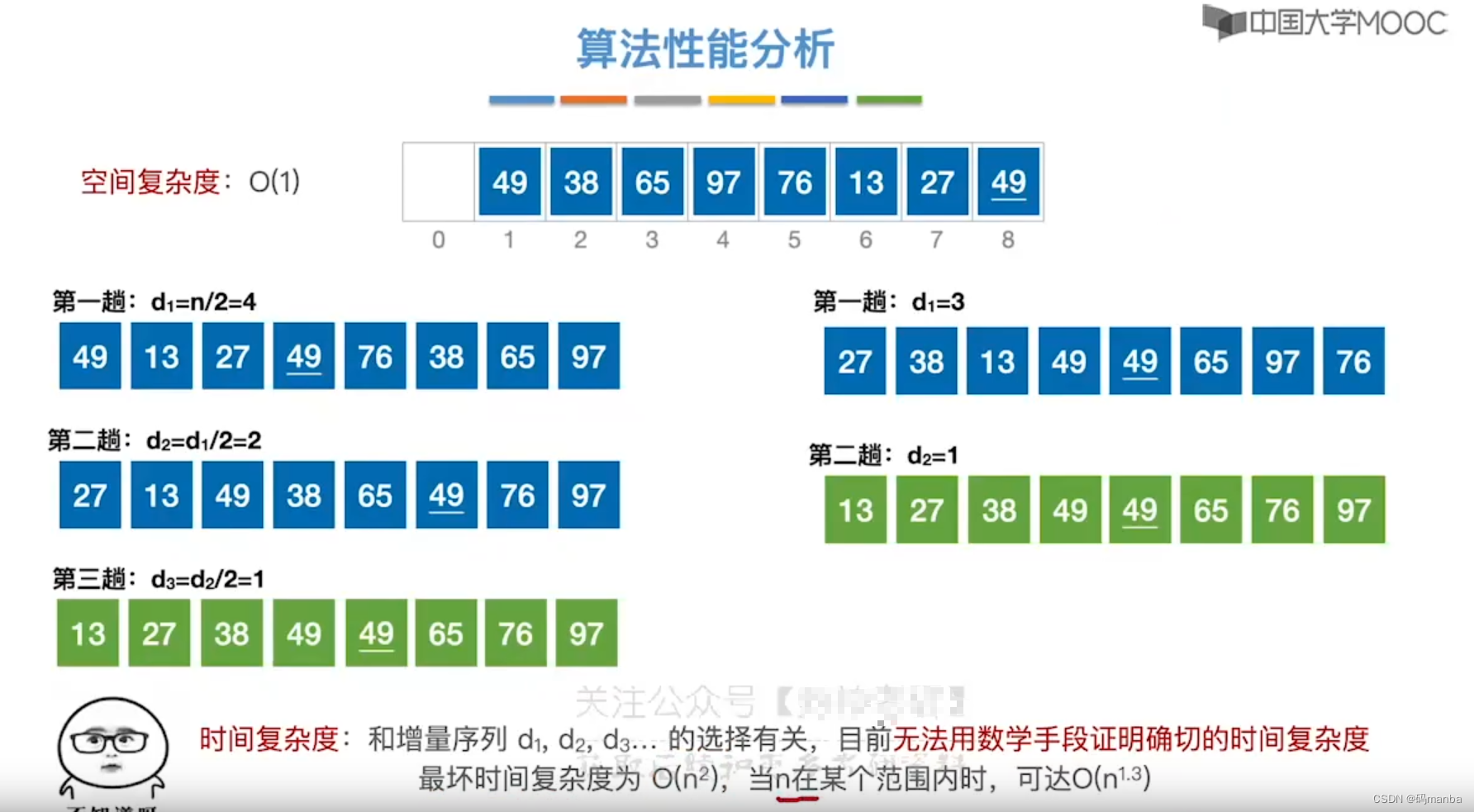
- 稳定性分析
- 不稳定
- 只适用于顺序表,不适应链表

希尔排序知识回顾
三、 交换排序
3.1 冒泡排序
- 代码描述图片已经标记
? 元素和前驱元素比较,采用 严格不等号; 在相等情况下不交换, 可以保证代码的稳定性;
算法实现
- 本算法是从后向前冒, 也可以从前向后冒;
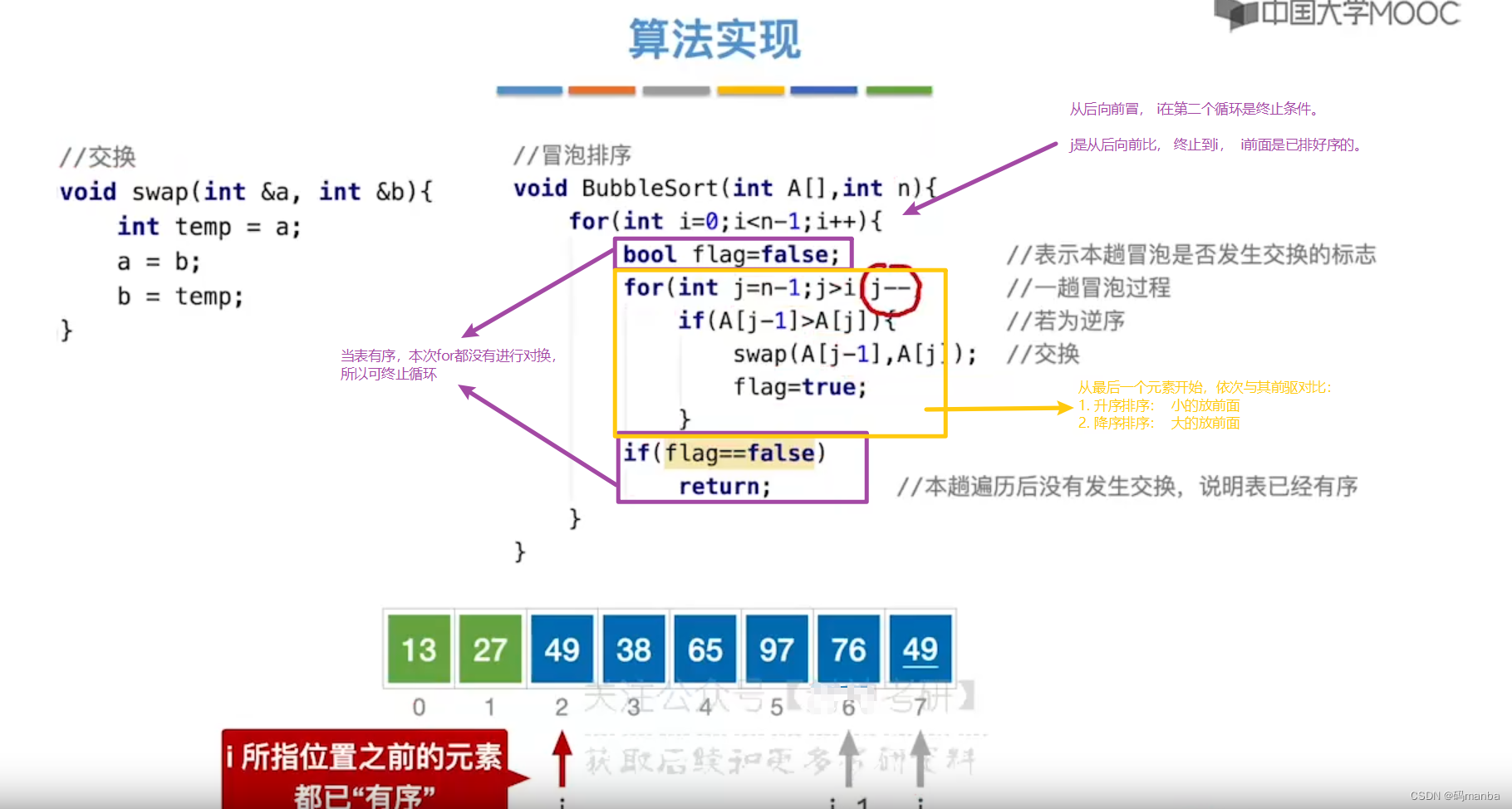
时间性能分析
- 时间、空间复杂度
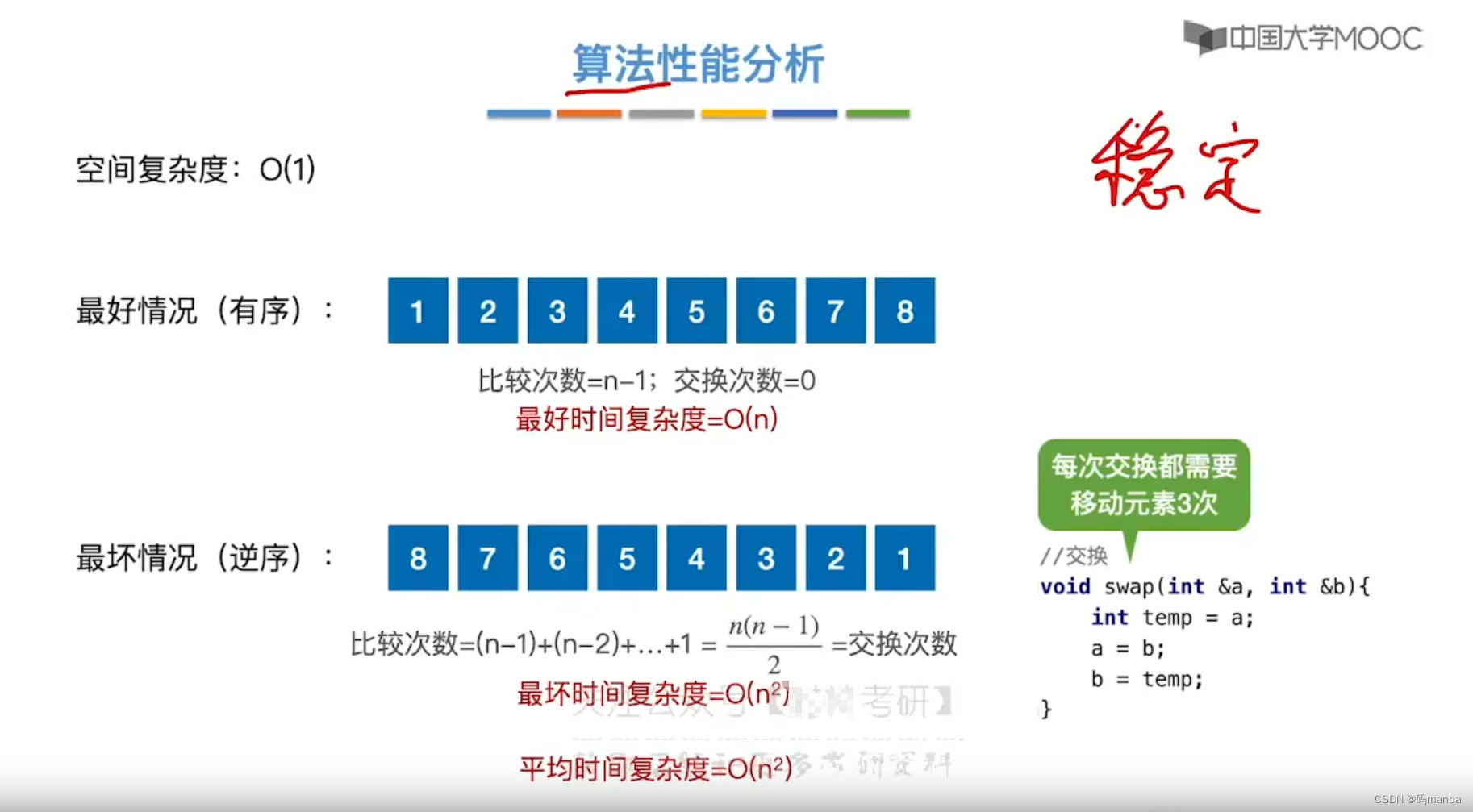
- 稳定性
交换条件严格不等号,稳定的。
- 存储结构,适用于链表也;
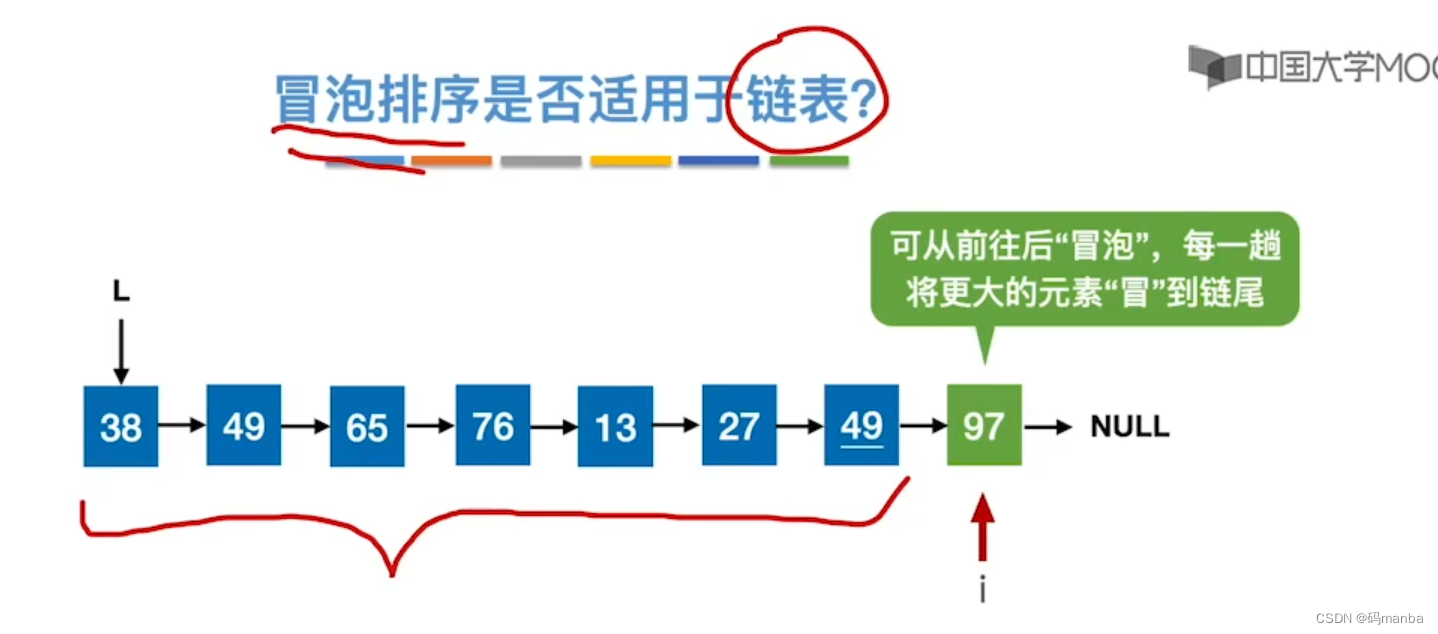
冒泡排序知识总结
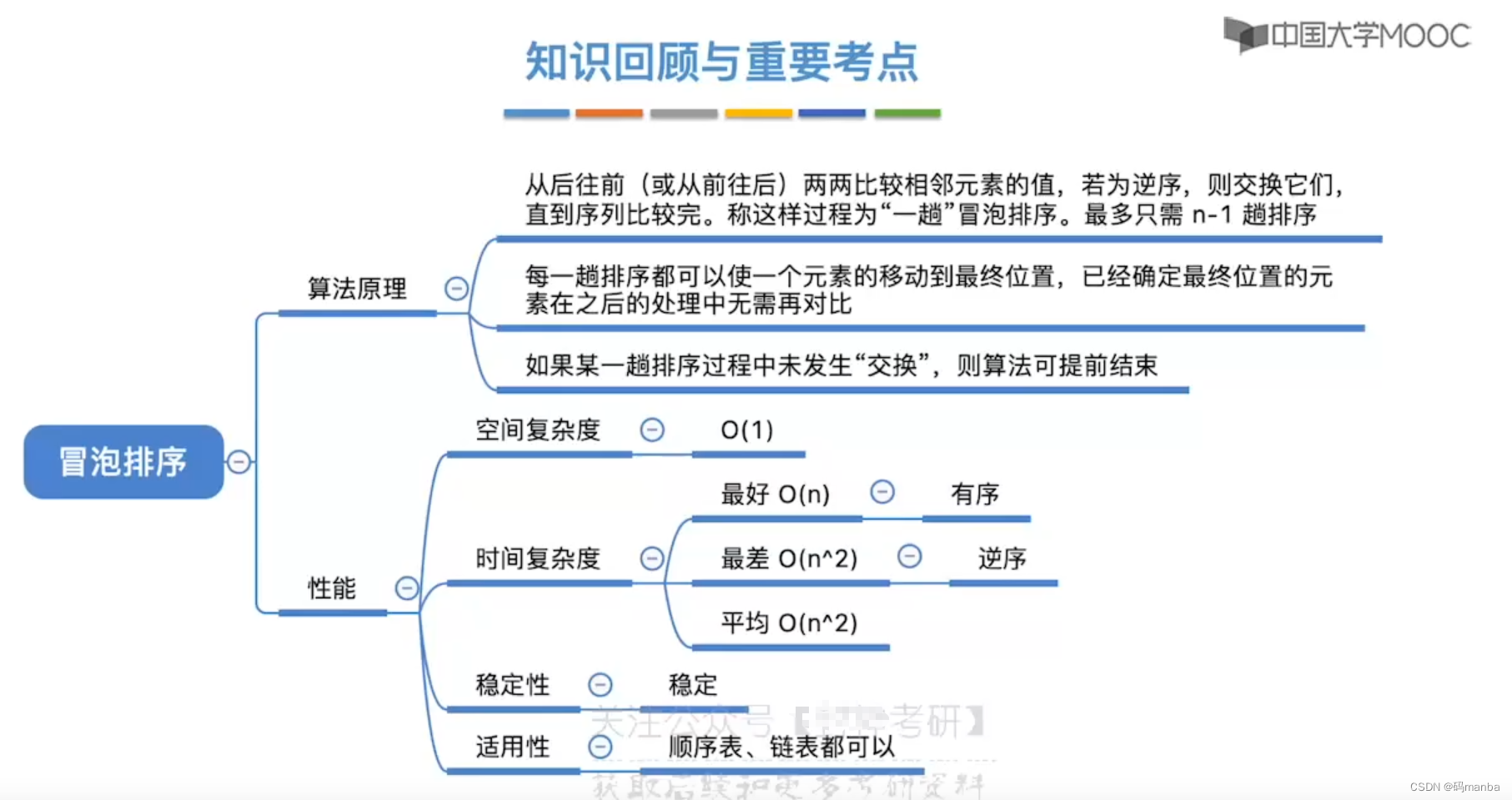
3.2 快速排序
快排实现思想
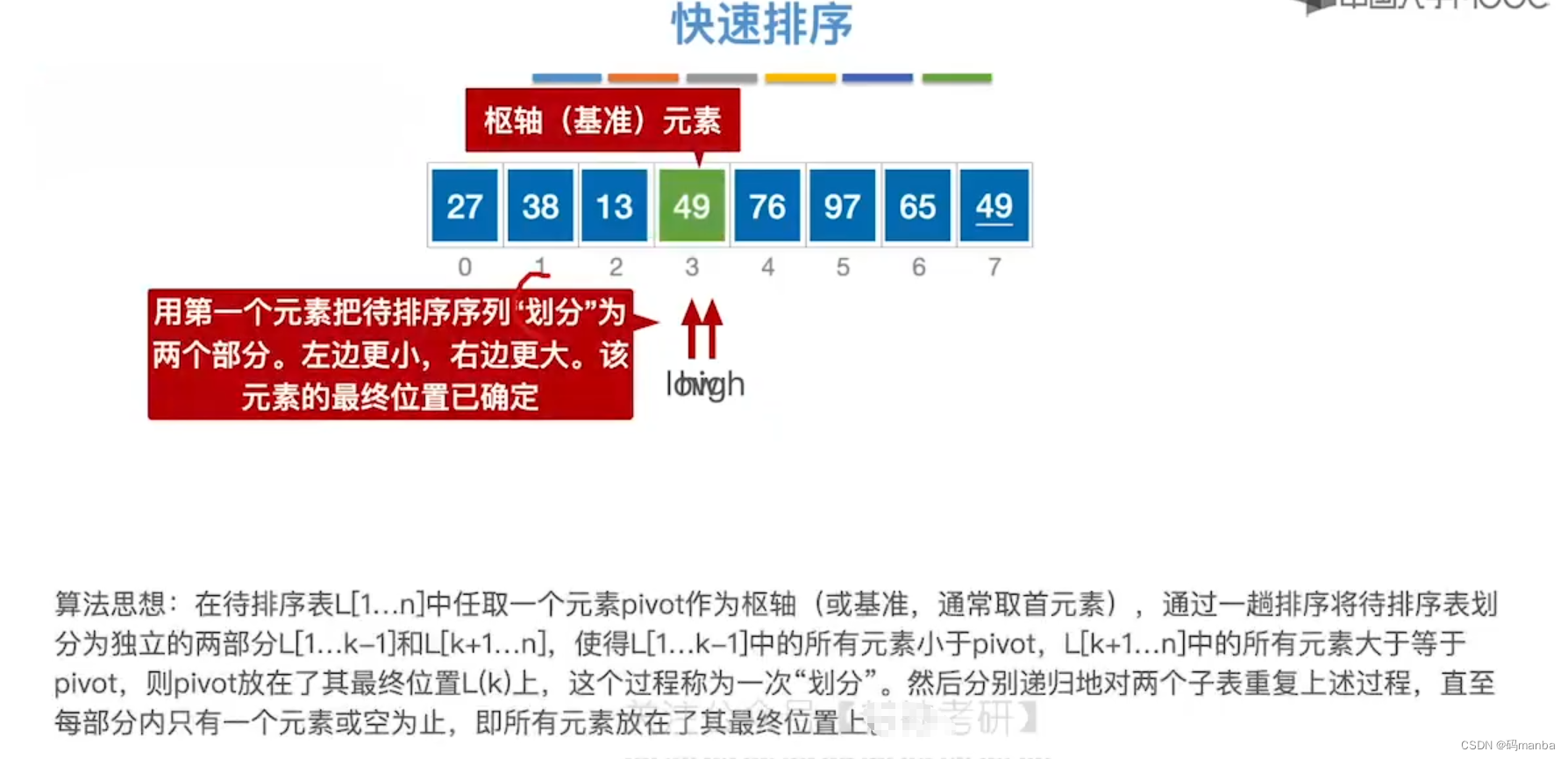
🌙 具体步骤
- 本次示例为中间部分, 快排的思想是
- 选中一个元素, 将其他元素与该元素进行比较, 小的在该元素左侧,大的在该元素右侧;
- 因此就会分离成两个 子表, 该元素左侧的子表均小于该元素, 右侧的子表均大于该元素
- 对左右子表在快排, 从而才分,直到全部确定为有序;
- 本次示例就是,一个子表的快排具体步骤
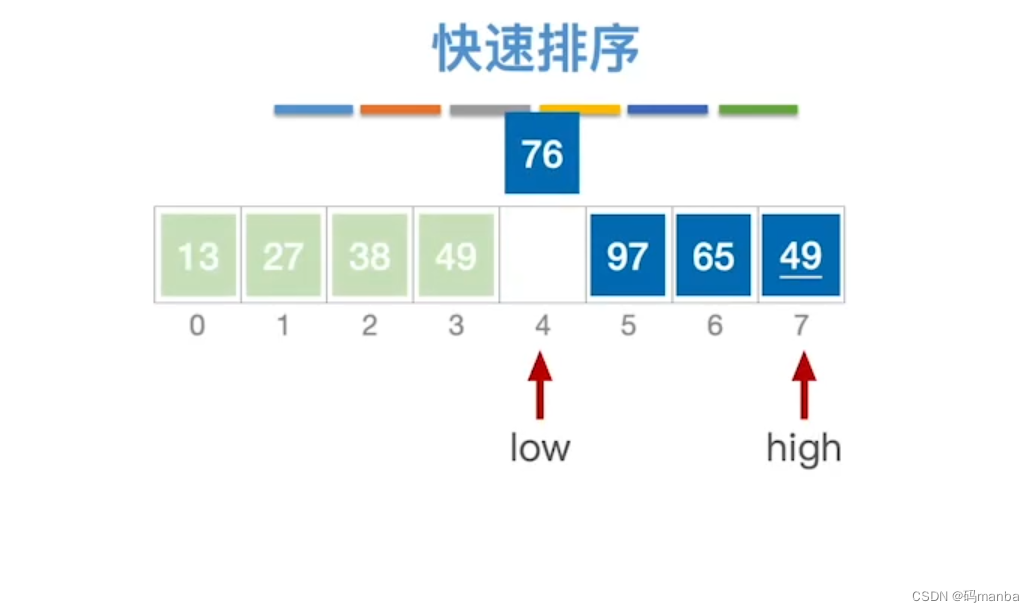
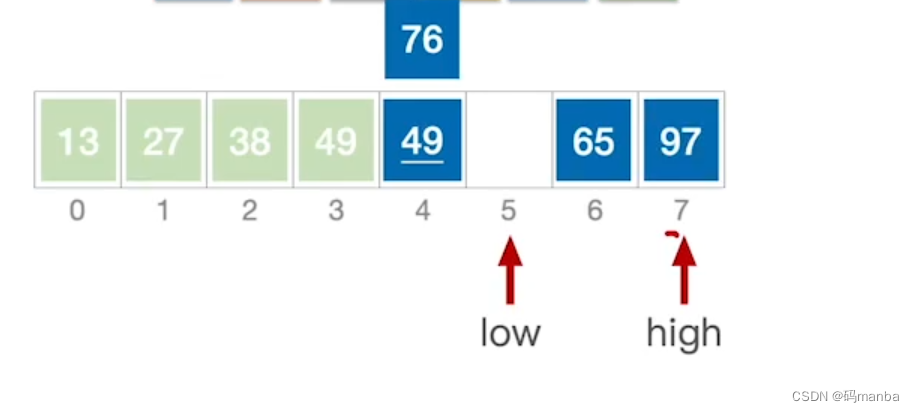
首先将最左侧元素确定
1.确定low(最左侧元素)、high(最右侧元素);
2.初始选择low指向的元素为基准元素(接下来每个元素都会与之比较,小在左,大在右,从而确定low的具体位置)
3.先比较high与基本元素,
① 如果high指向的元素小于基本元素, 将其移动到low指向的位置;
② 如果high指向的元素还是大于基本元素, high指针继续左移,直到找到小于(严格小于)基本元素的位置;
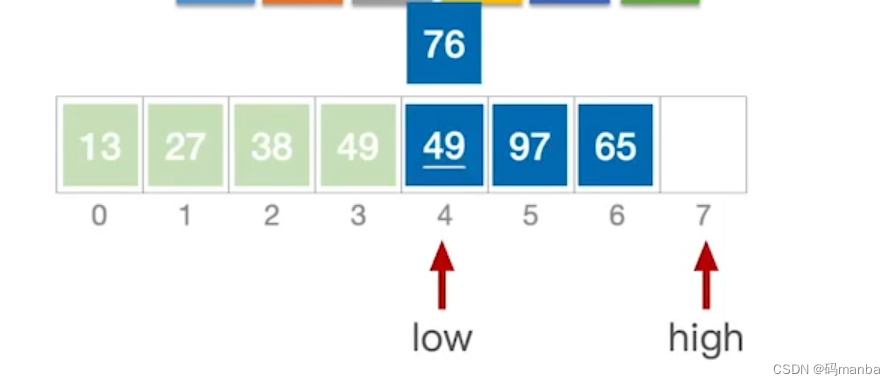
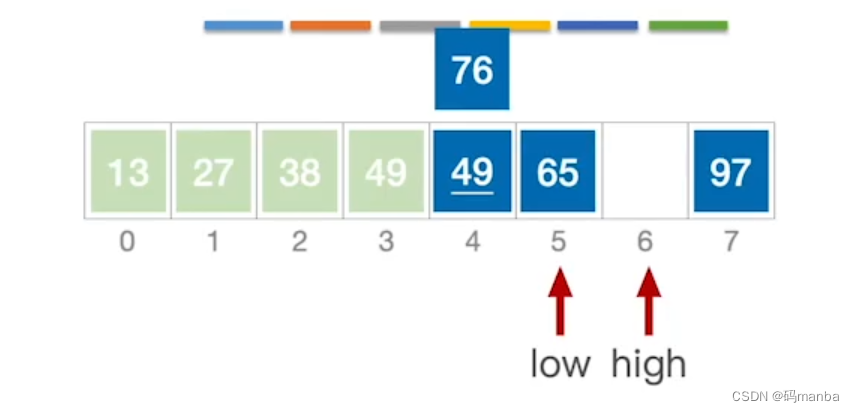
4.然后low此时应该向右移动,然后low新指向的元素与基本元素比较,
① 如果low指向的新位置大于的话就将其放置到high的位置;
② 如果low指向的新位置还是小于基本元素,那么low继续右移,直到找到大于(严格大于)基本元素的位置;
5.再切换到high,high左移,比较high指向的元素是不是小于基本元素,如果小于则,将high指向的元素移动到low指向的位置;
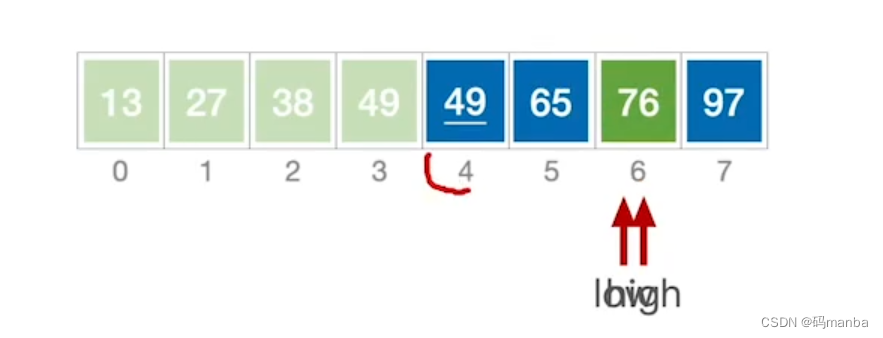
6.再切换到low,low向右移动, low和high碰头,就将基础元素,放到low和high共同指向的位置;
快速排序的算法实现

时间效率分析
- 时间复杂度: O(n * 递归层数) (时间复杂度和递归层数息息相关)
- 空间复杂度: O(递归层数) (也与递归层数有关)
? 所以研究空间、时间复杂度,先研究递归层数


? 递归调用的次数,和其排序好的序列转换成 二叉树树的深度最高、最低有关
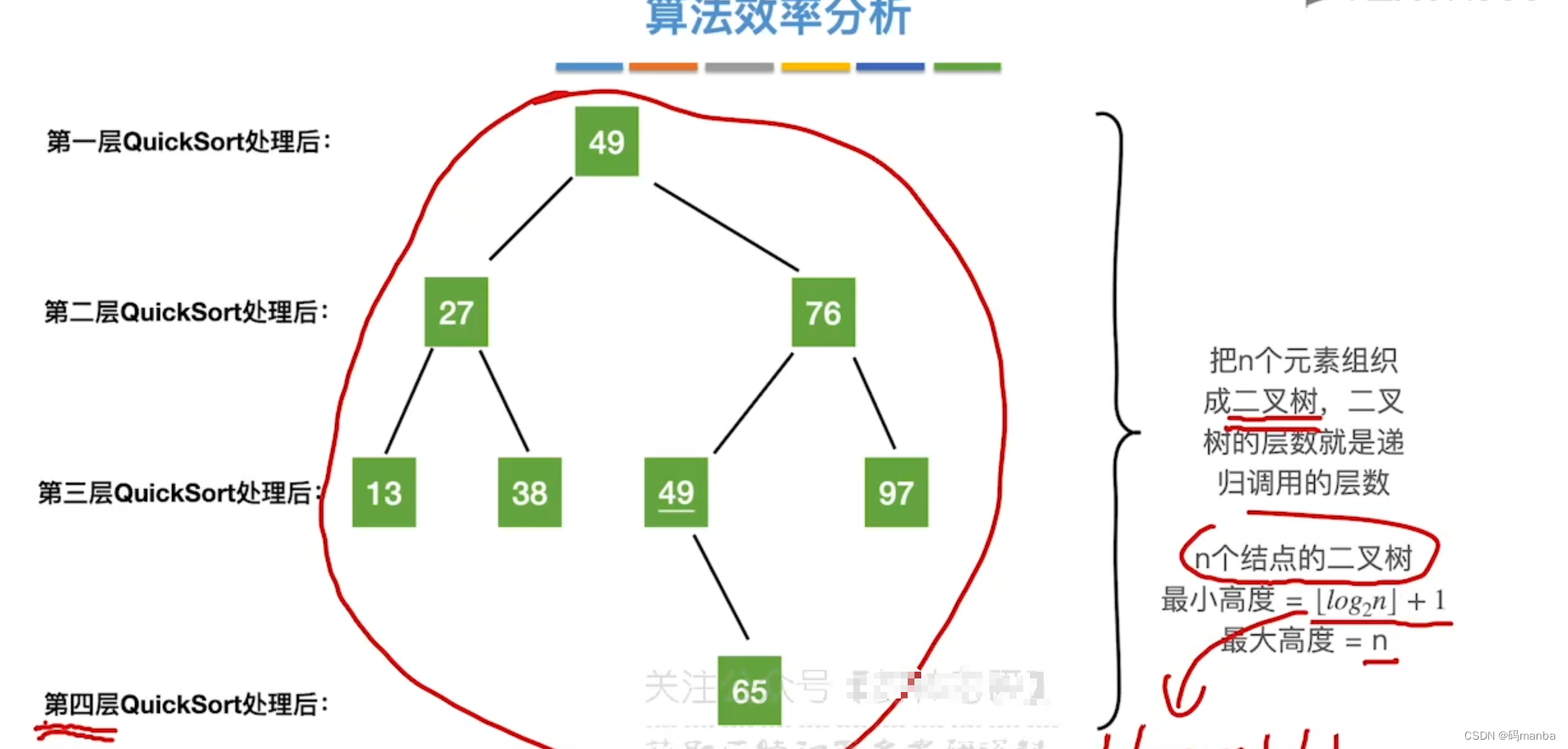
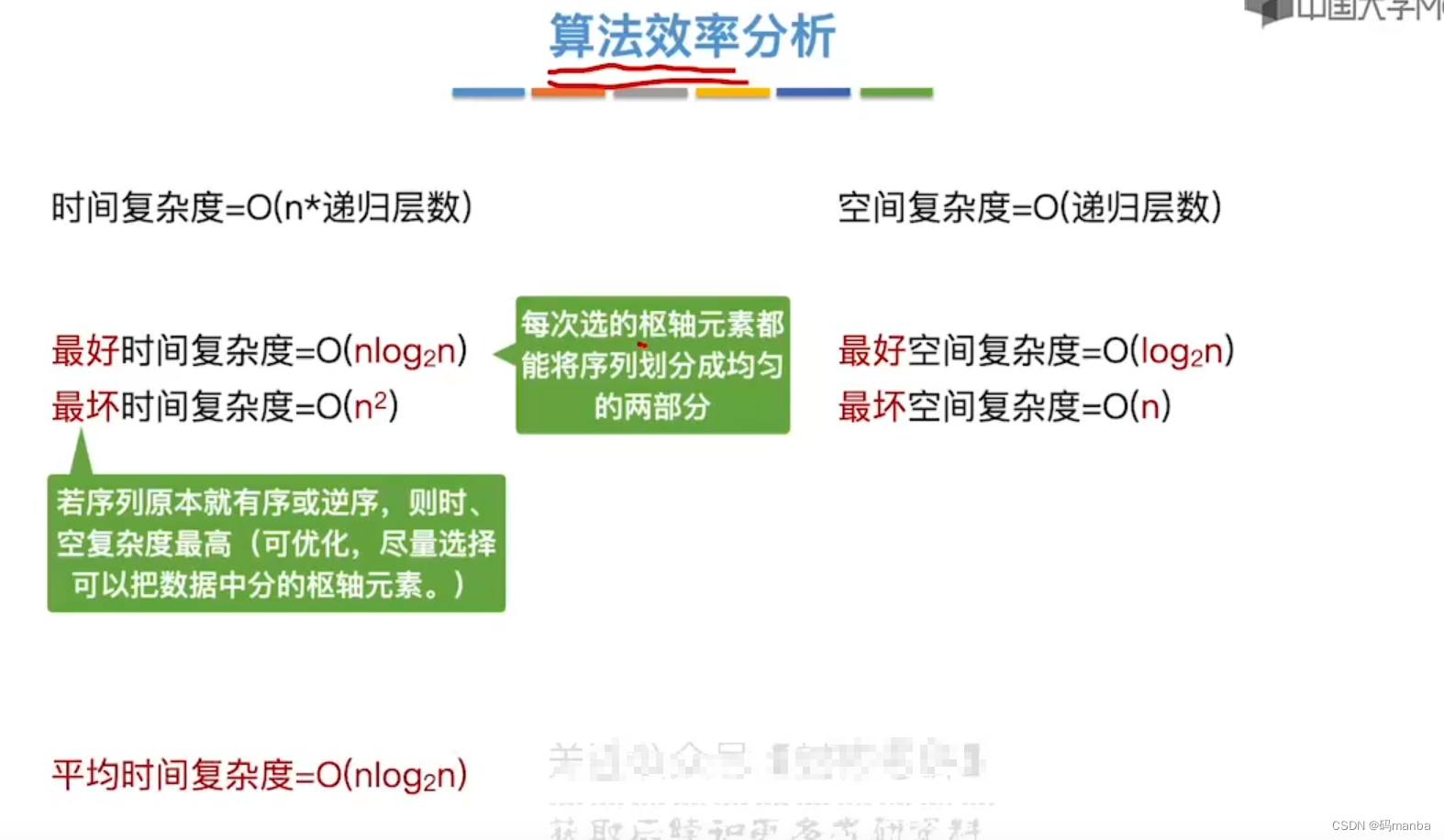
? 快排效率总结

? 稳定性
- 不稳定

优化快排
- 每次选取low作为枢轴元素的时候,如果排序的序列是有序的,每次分割的两个部分都会最不均匀,费时最大。
- 但是如果每次选择的 枢轴元素放到指定位置后,将分割的两个部分比较均匀,则算法效率值最高。
- 介于此,可以采用 如下方案进行优化快排;
- 选 头、中、尾三个位置的元素取中间值, 作为枢轴元素;
- 随机选取元素作为枢轴元素;

快速排序知识点总结

注意 408的代码实现的 “一趟排序” 和 “一次划分” 的概念
- 一次排序是否等于一次划分, 一定要从代码实现上去分析。
- 假如一趟排序后, 只确定一个枢轴的位置 , 就是等于一次划分的;
- 如果一趟排序后,可以确定多个枢轴的位置,就是等于多次划分的;
- 一次划分其实就是一个partition函数的执行,而一趟排序可能执行两次parttion函数。


四、 简单排序
4.1 简单选择排序
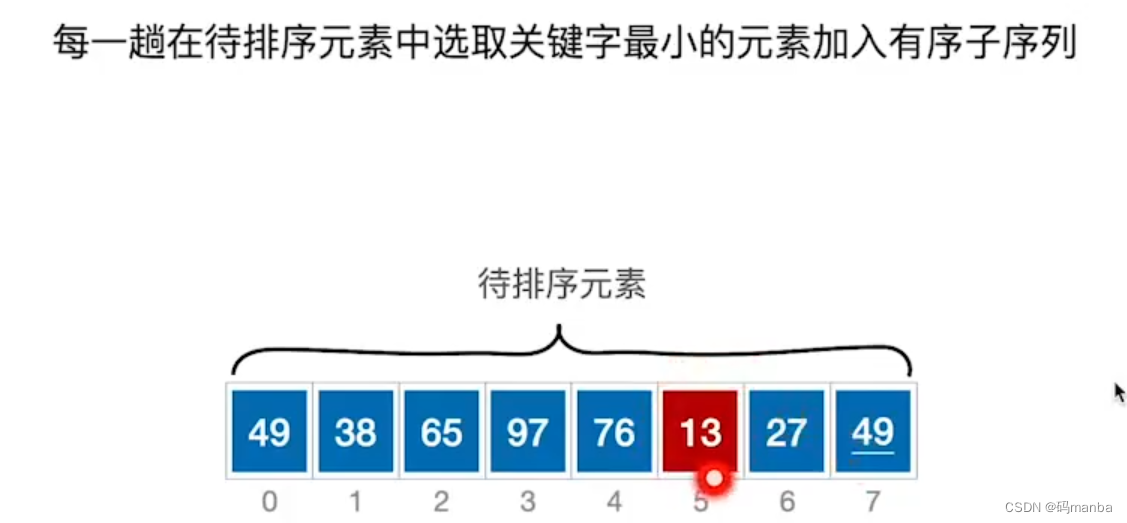
简单选择排序的实现过程
- 选择一个关键字最小的元素,然后与前面的位置进行交换
交换后2. 在余下的元素中选择关键字最小的
再交换
3. 如此直到最后一个元素,而最后一个元素就不用比较了,因此就是需要n-1次处理;
简单选择排序的代码实现
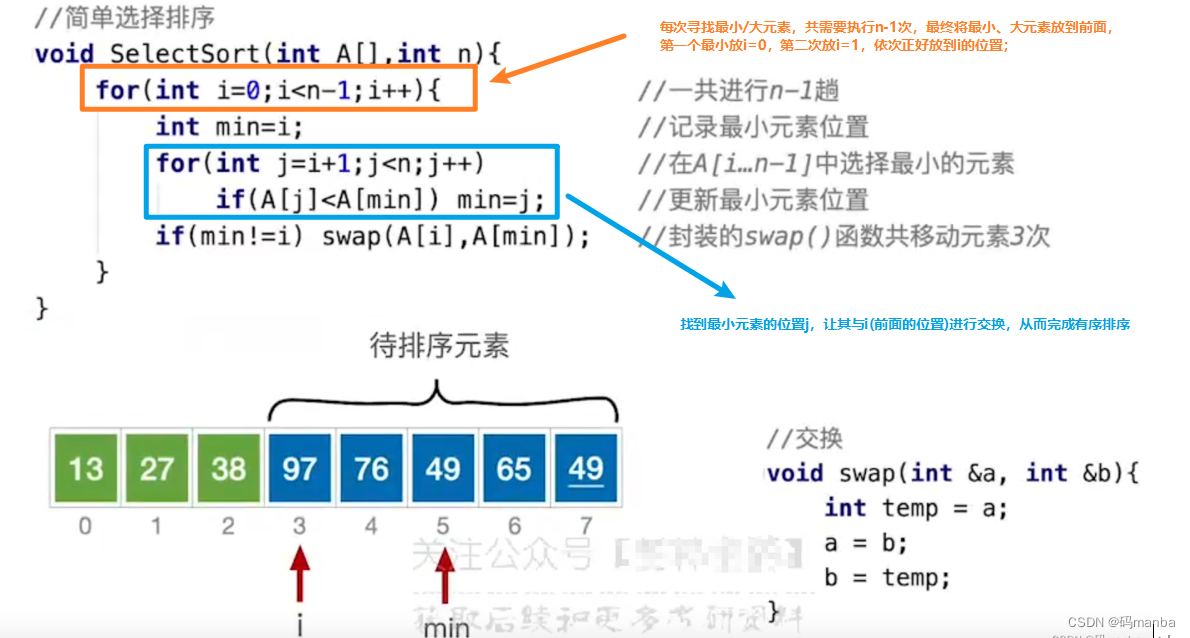
算法性能分析
- 时间复杂度与空间复杂度;
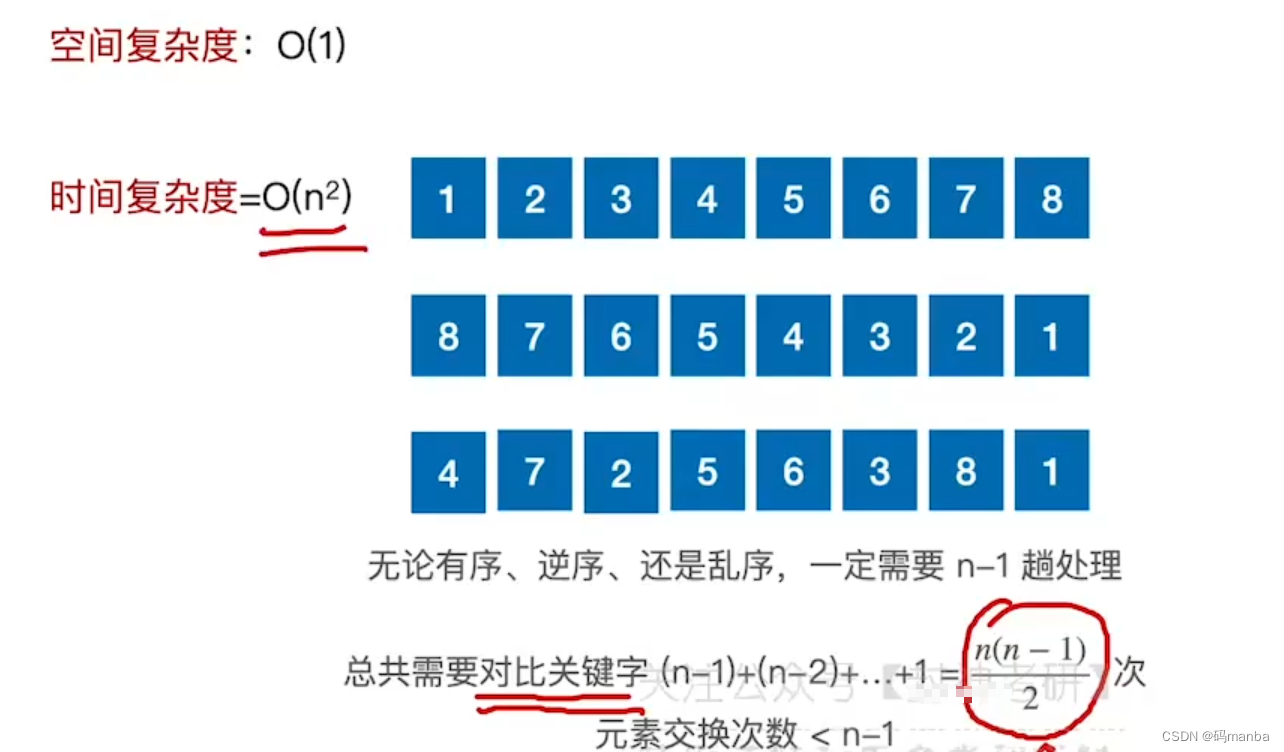
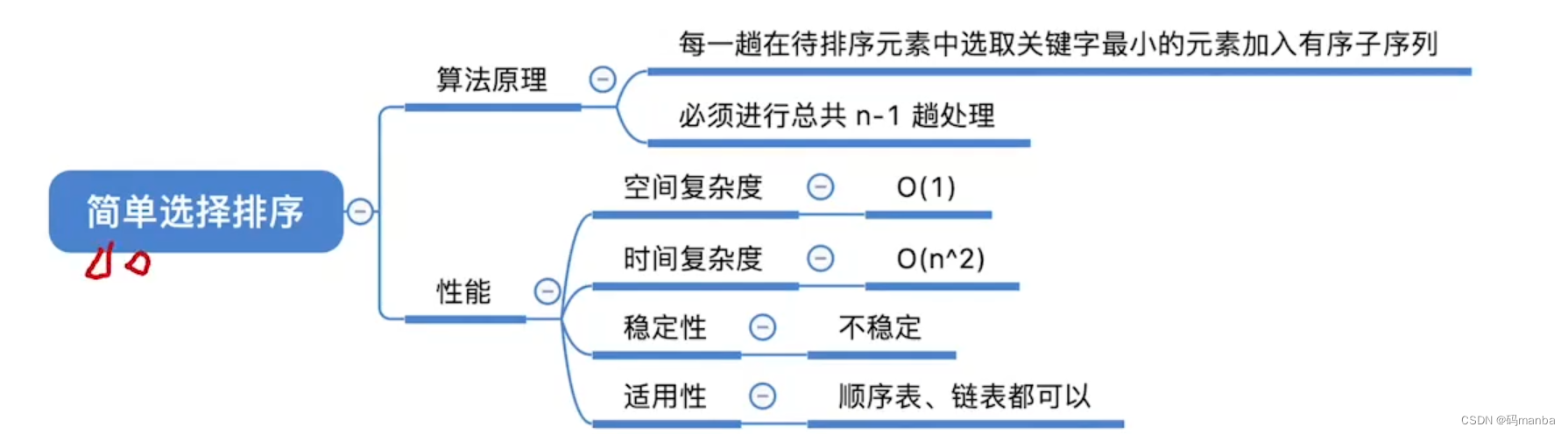
- 稳定性:不稳定;
- 既可以通过链表实现,也可以通过链表实现;

简单快速排序的知识总结
- 简单排序算法,并不会因为给出的元素的出场顺序不同,从而导致时间复杂度不同。 反而它的时间复杂度一直是o(n^2)
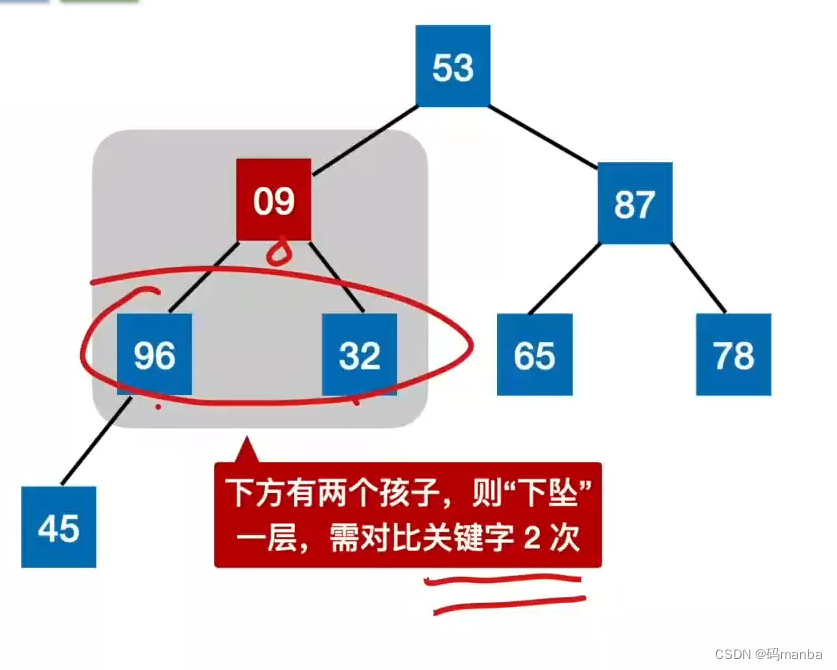
4.2 堆排序
概念补充
? 完全二叉树顺序存储的知识
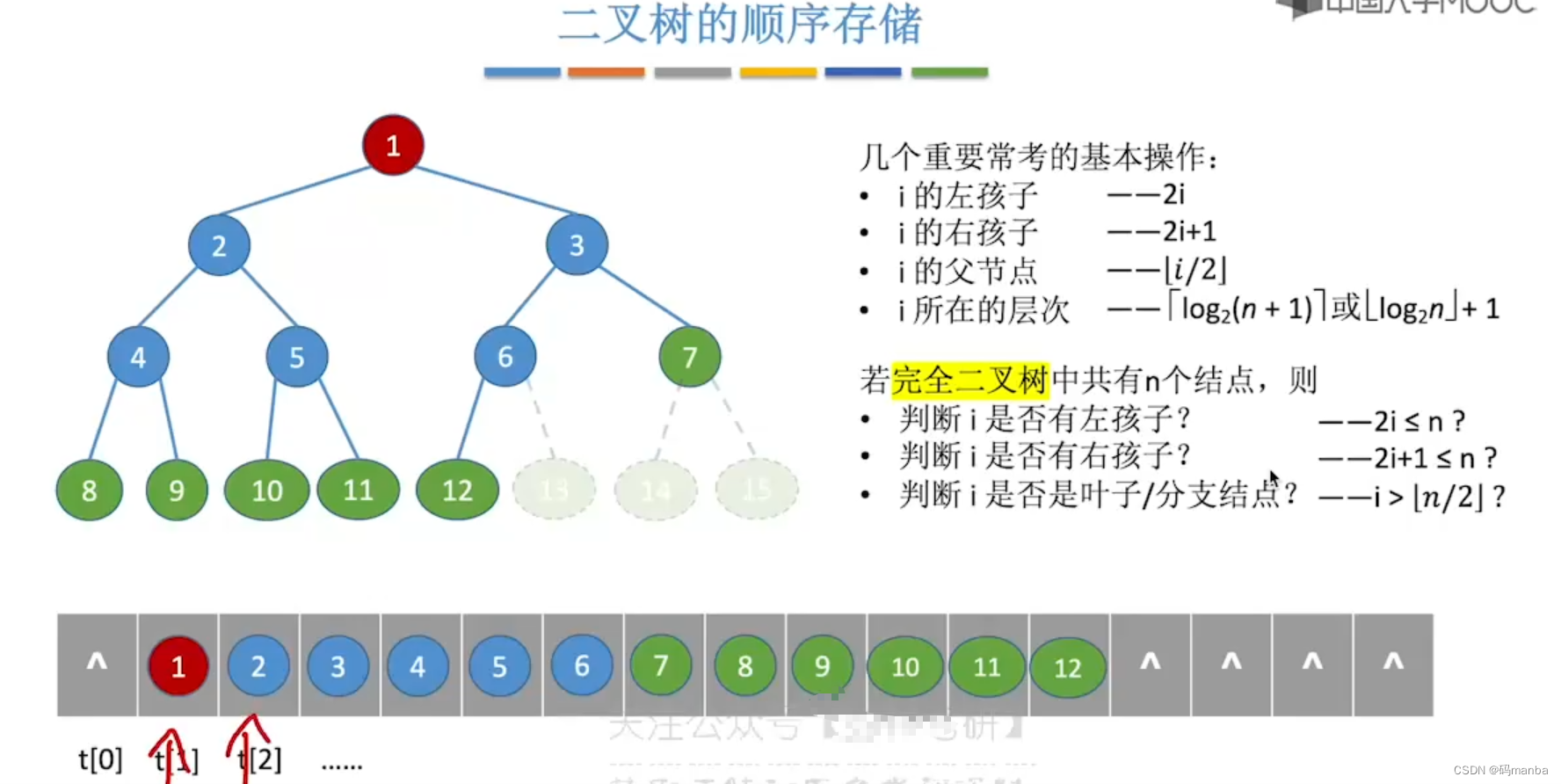
? 大、小根堆
- 大、小根堆可以想想成,顺序的存储结构,转换成一颗完全二叉树后, 根结点与左右结点比较,根大大根堆,根小小根堆;
- 所以说,大根堆,初始元素一定是最大的,小根堆初始元素一定是最小的。所以根堆的存储方式,进行选择排序将异常的方便;

? 大根堆
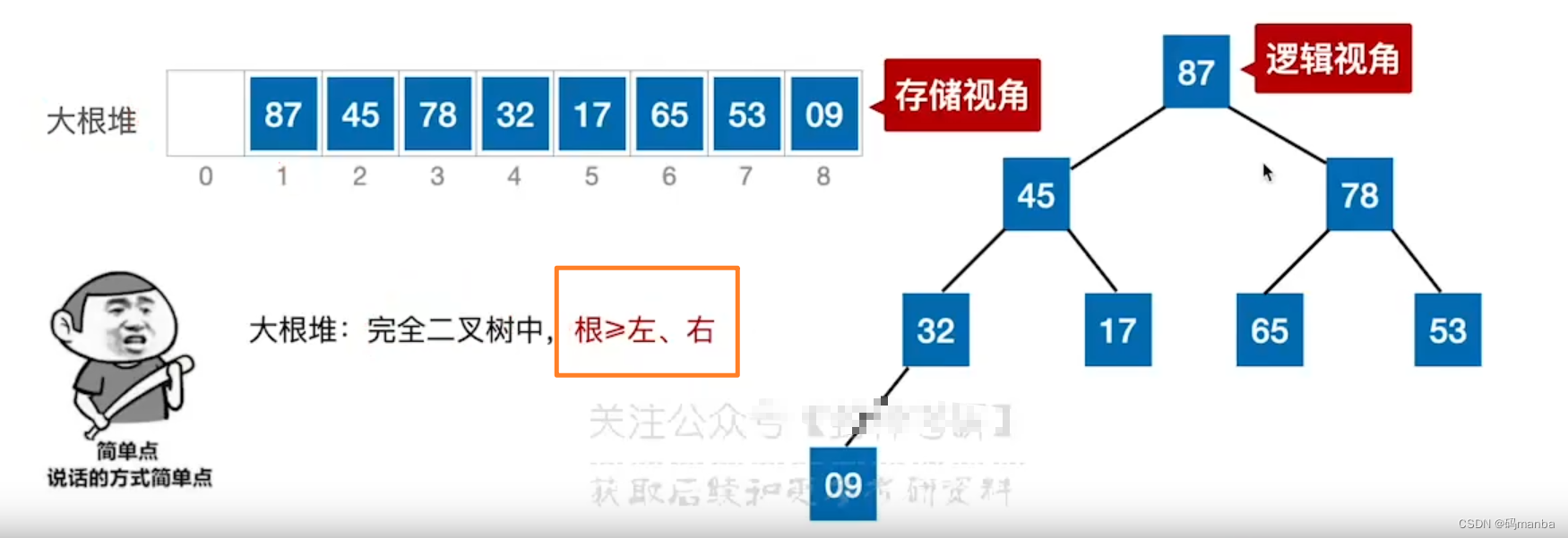
? 小根堆

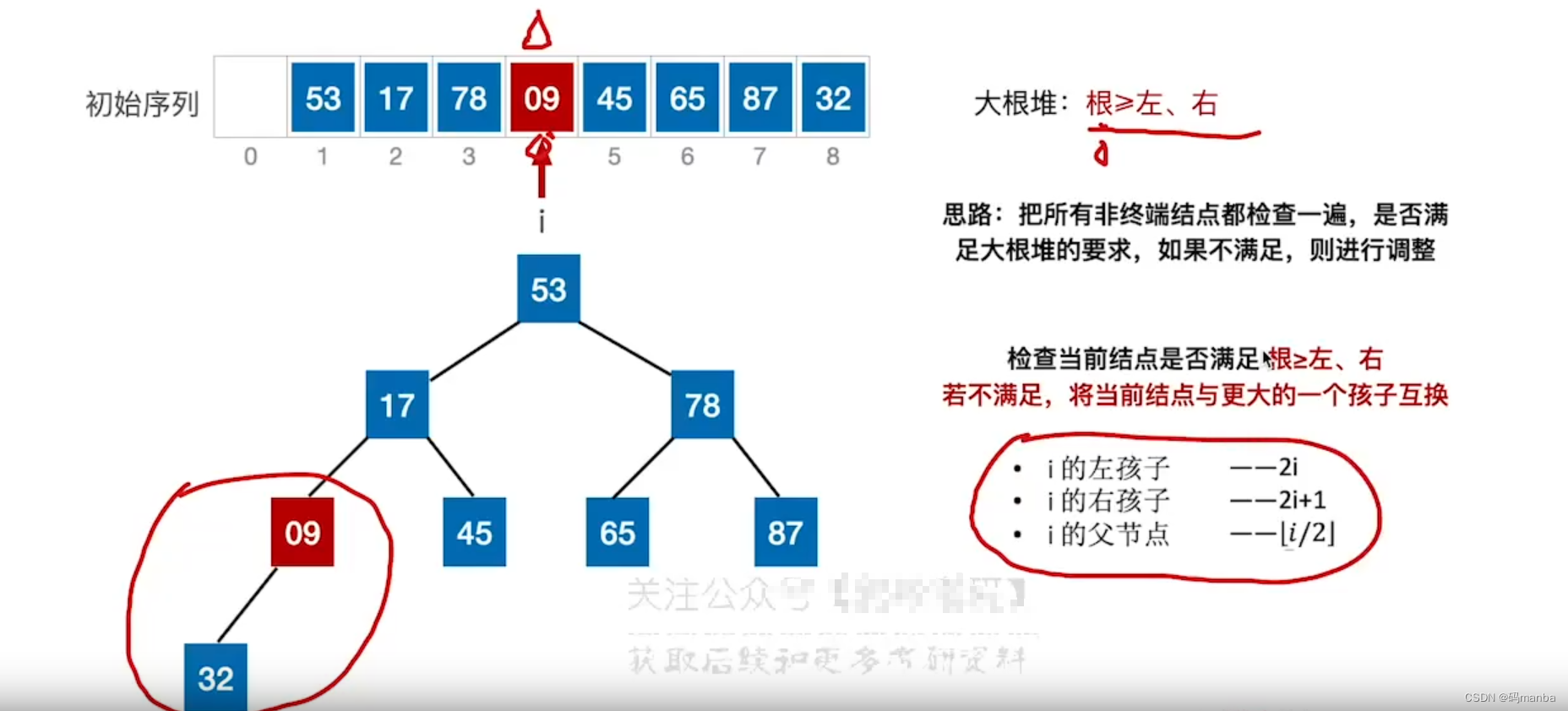
根据初始序列建立大根堆
? 口诀: 根小根下坠, 根换大孩子。
- 检查所有的非终端结点(i<[n/2] 向下取整)是否满足大根堆(根大于其左右孩子) ,n是元素个数;
2. 如果不满足(根不大于左右孩子), 将根和更大的左右孩子进行互换。
换完后
3. 再检查下一个中间结点(【n/2】向下取整 - 1), 如果不满足大根堆特性(根大于左右孩子),则与更大的孩子进行互换。
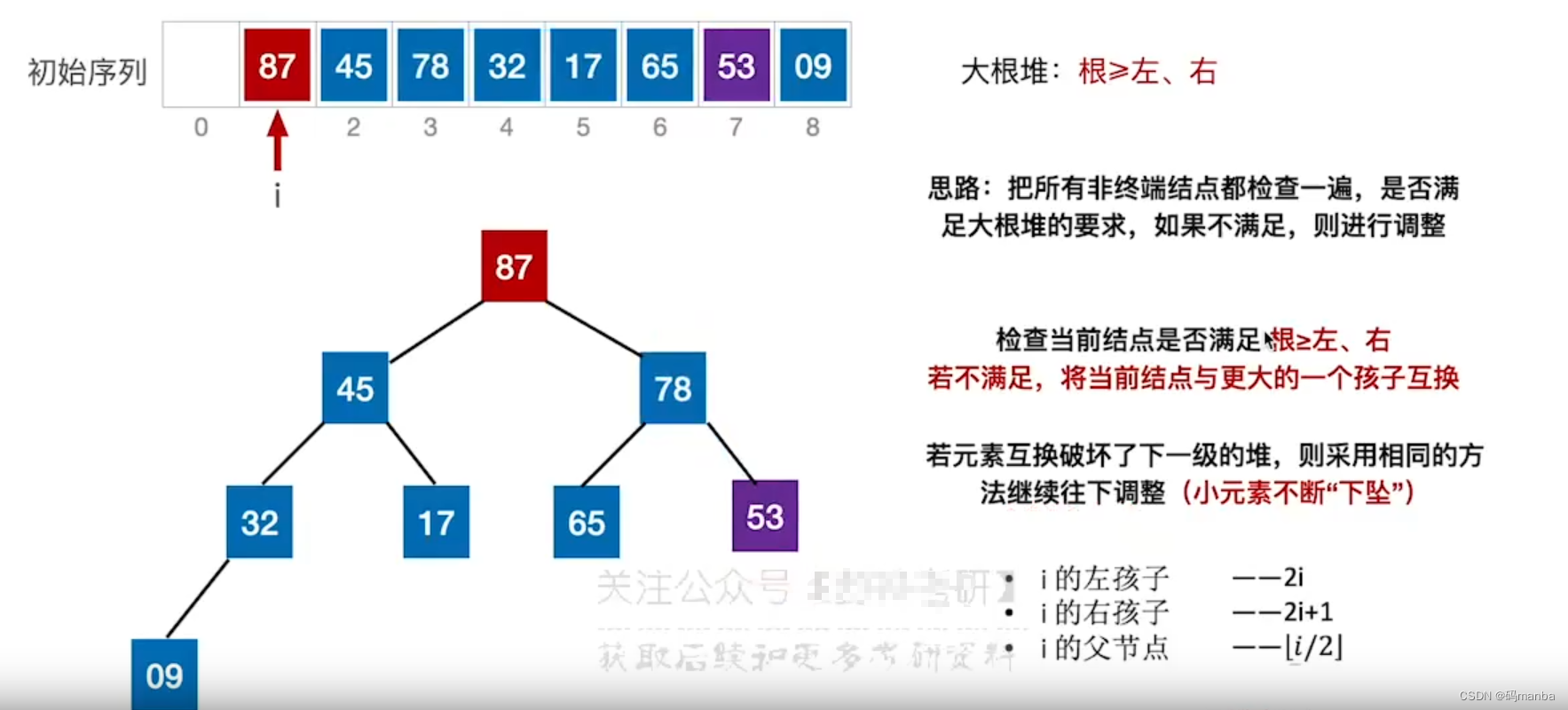
4.如果在处理大根堆时,根结点与较大孩子结点互换(在树根位置)出现换完后孩子结点小于其左右子树
则也印个相同的方式向下调整,较大的子树与根结点互换。
建立大根堆的代码
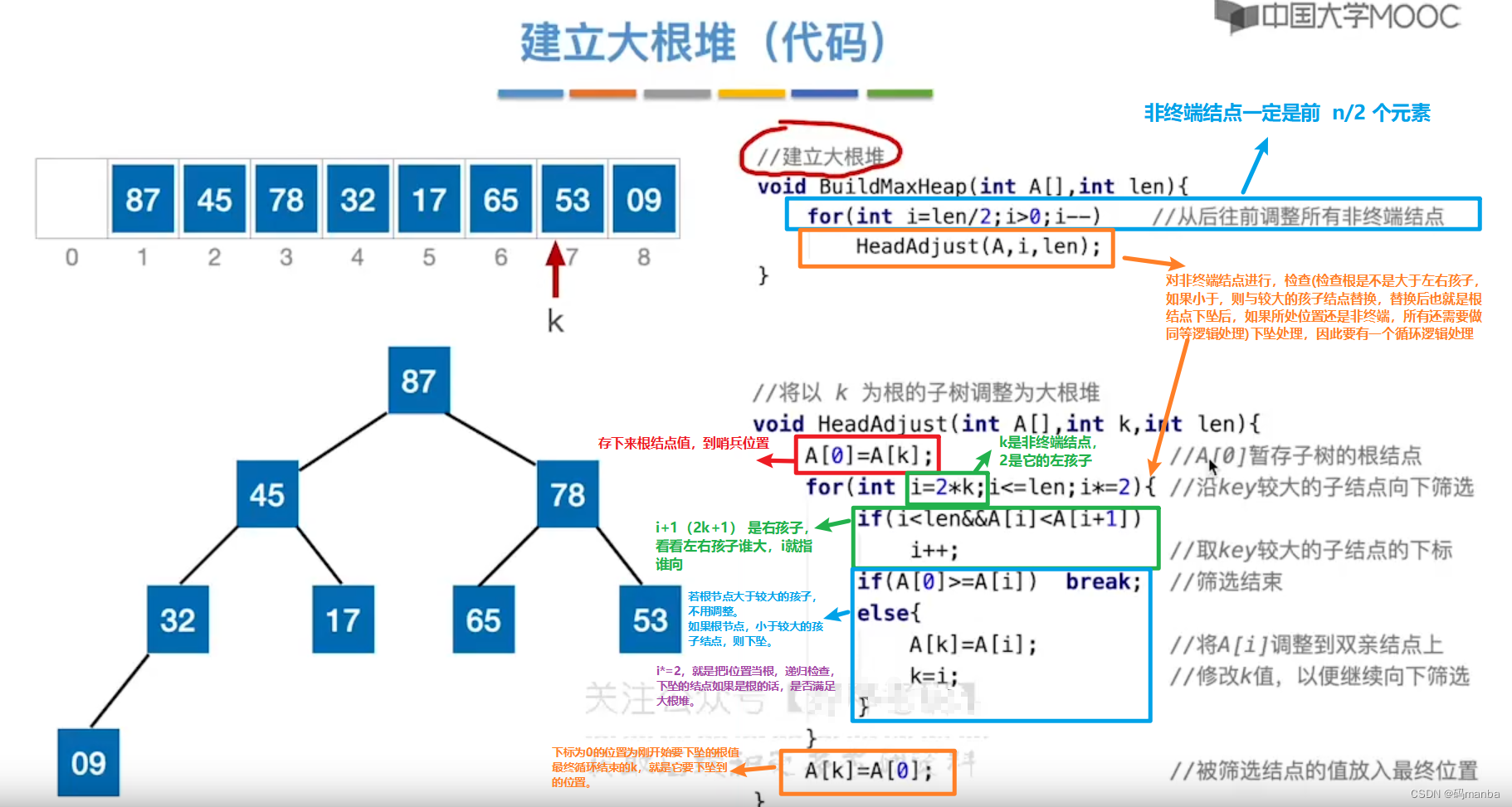
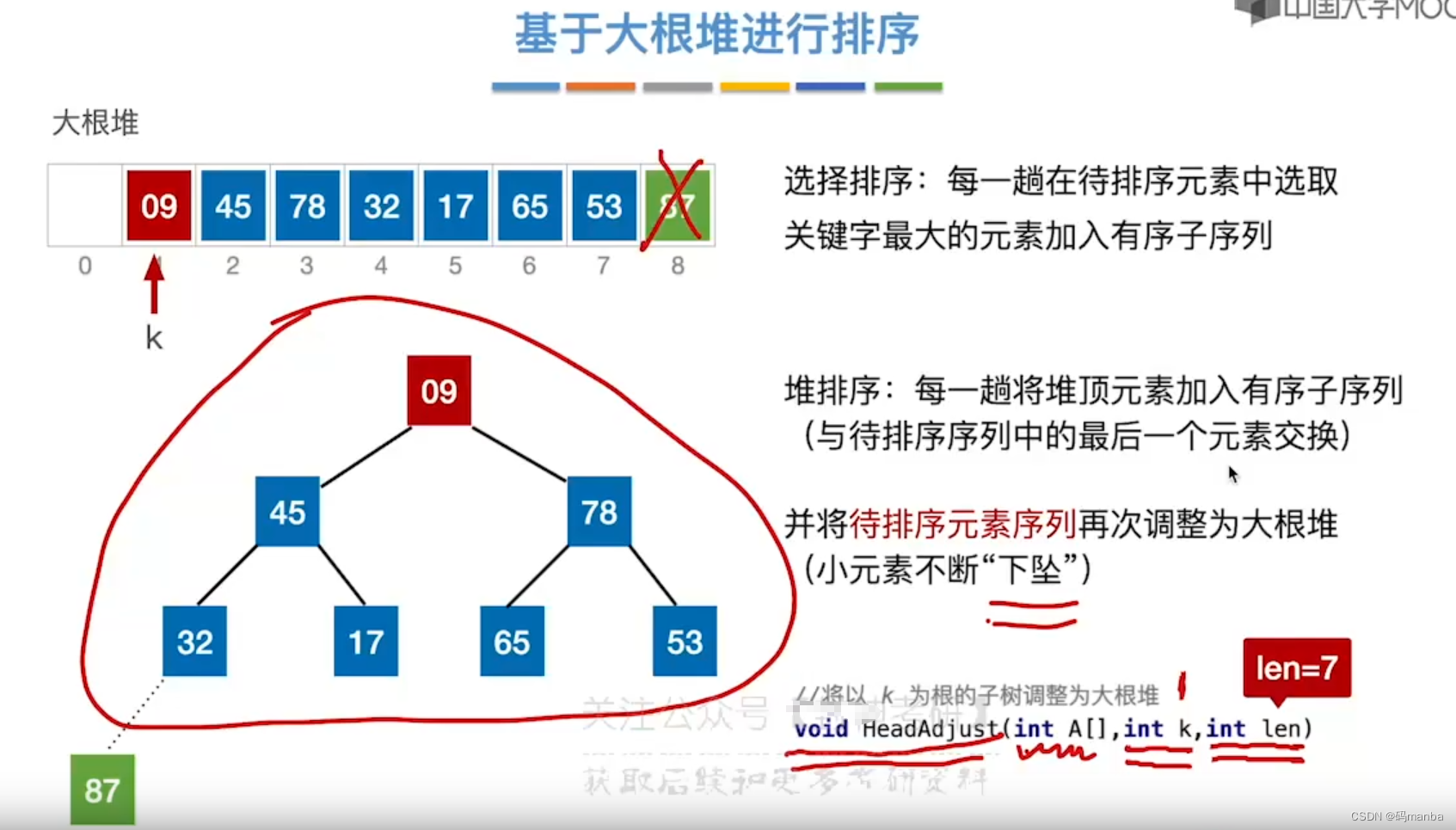
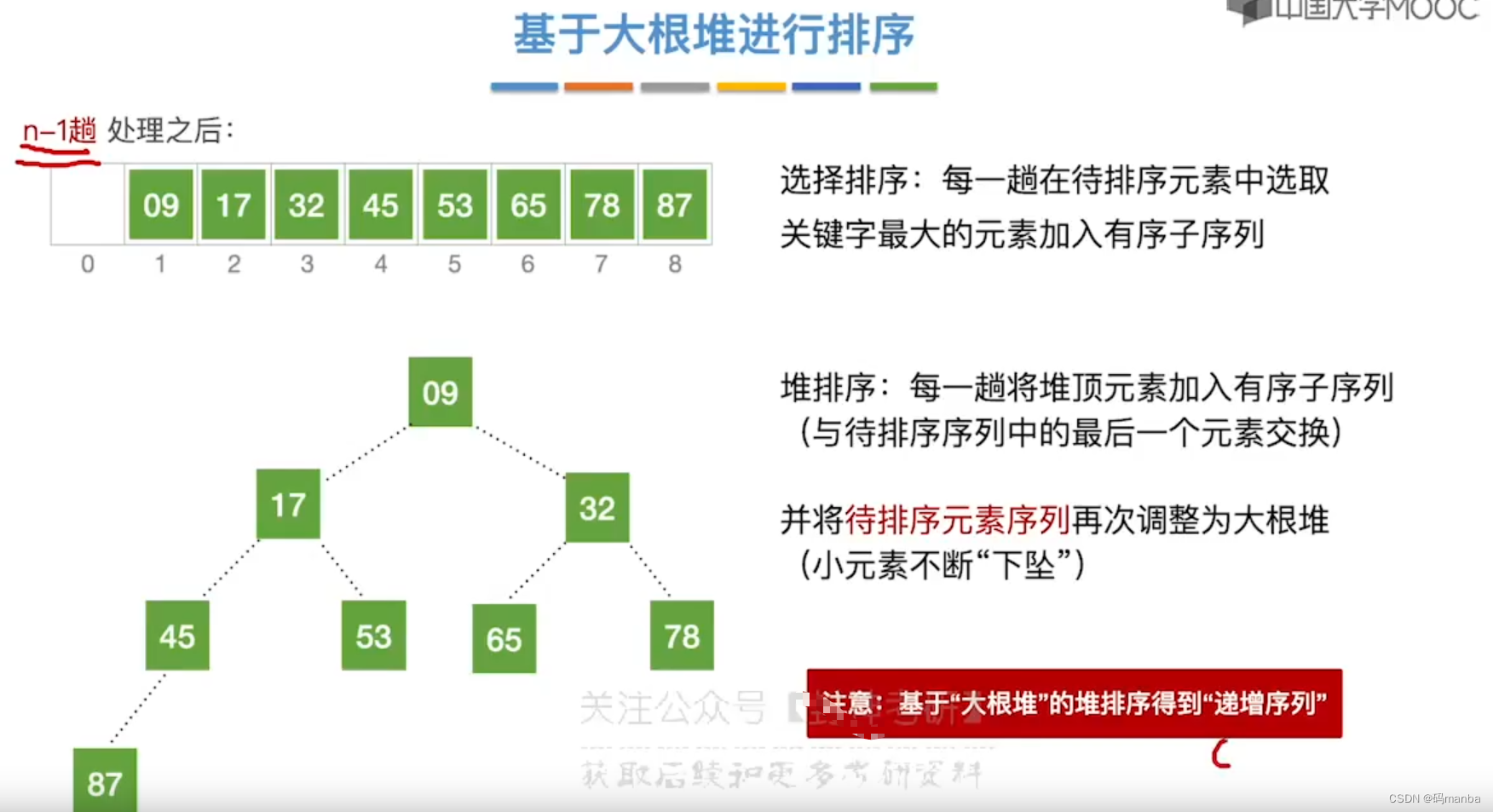
基于大根堆进行排序的思想
- 🌙这种替换思想是不基于额外存储空间的条件下执行的。
?1. 首次将堆顶元素与最后一个元素交换(就是堆顶元素加入有序序列)
87也就是大根堆的堆顶就是有序序列第一个元素,交换后,堆顶元素并不是最大的,因此需要进行大根堆的调整函数HeadJust(剩余序列,k为根,长度)
调整后,又成为大根堆存储结构
?2.重复步骤一
1.堆顶加入有序序列(不需要额外空间,和序列尾部元素对换就行)
2.然后又排序大根堆,再调用大根堆排序函数
?3.进行n-1趟 处理后, 基于大根堆的堆排序就会得到一个递增的序列,因为每次都是堆头(大根堆队头元素最大)和队尾元素换。
堆排序完整代码(建立大根堆,下坠调整,基于根堆的选择排序 )
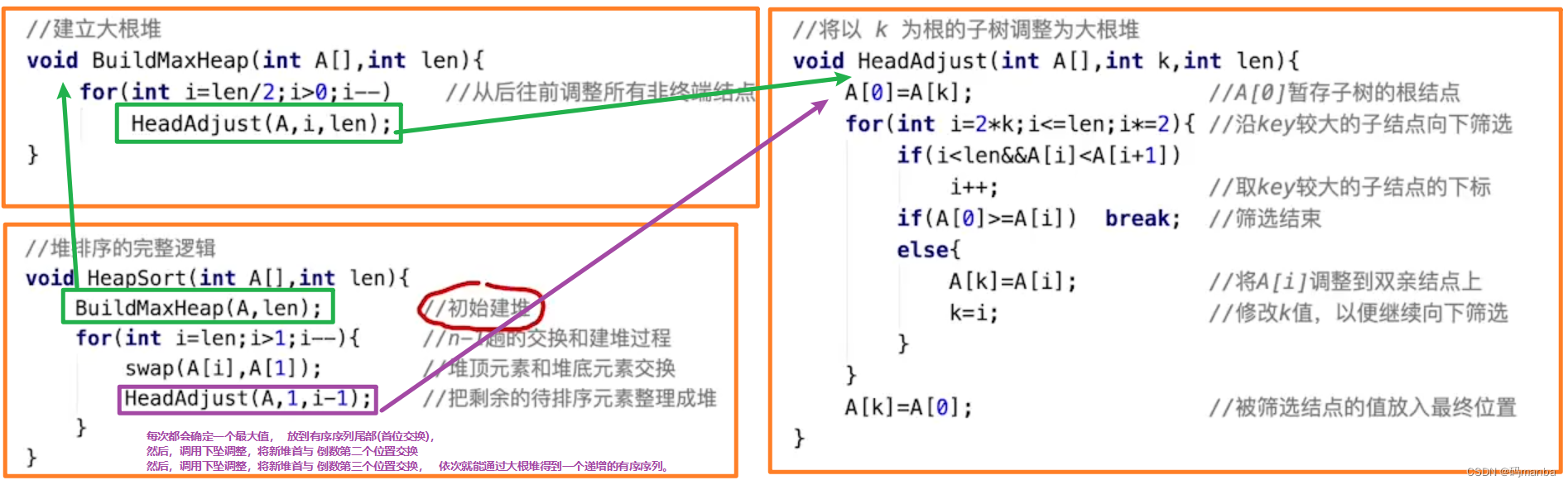
算法效率分析
- 时间、空间复杂度


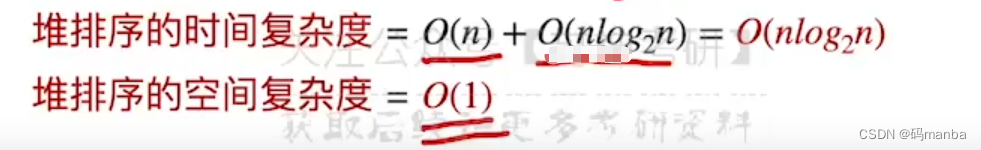
- 稳定性

堆排序知识小总结
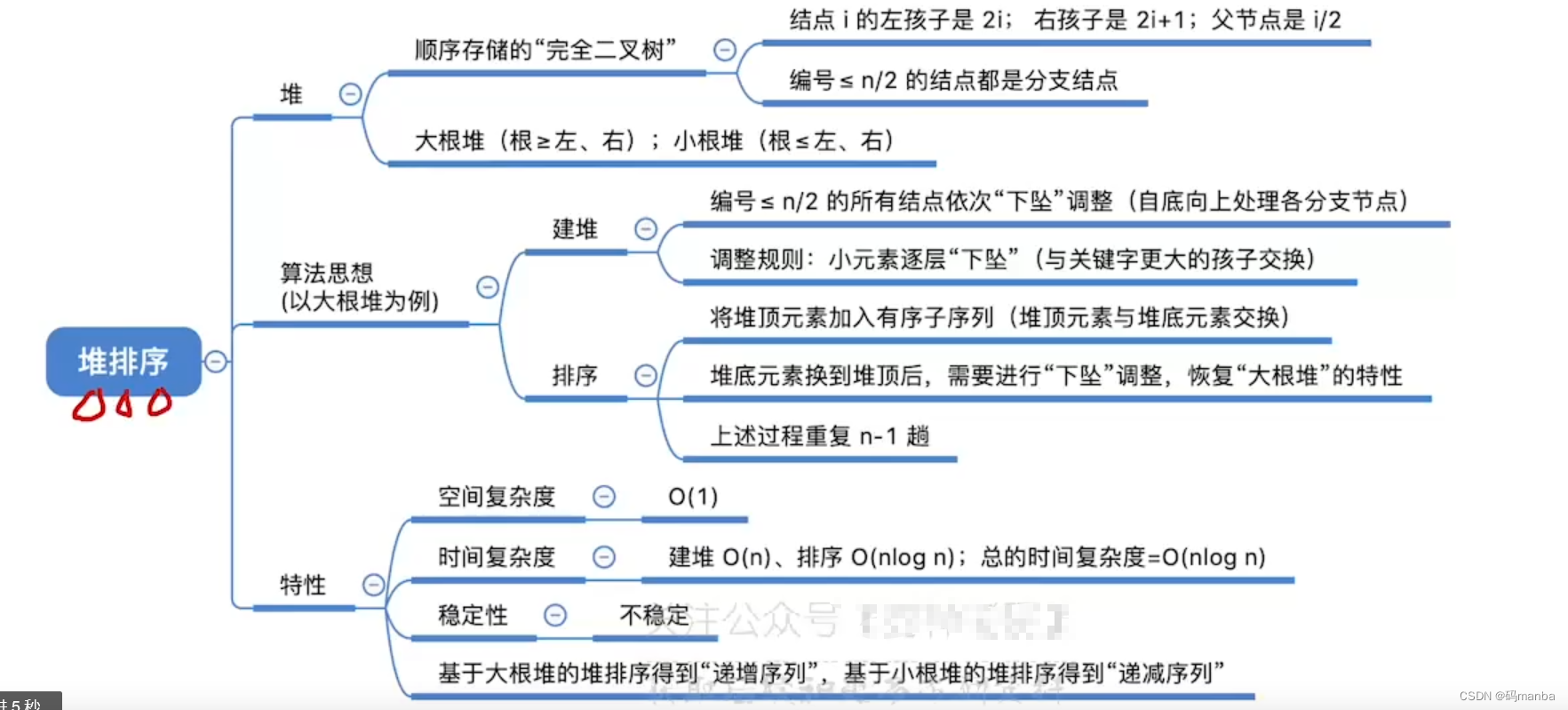
小根堆内插入元素
- 1.首先将新元素放到表尾
- 2.新元素与其父结点进行对比,如果小于父节点,就交换。
- 3.上升后再对比。直到大于父节点为止。
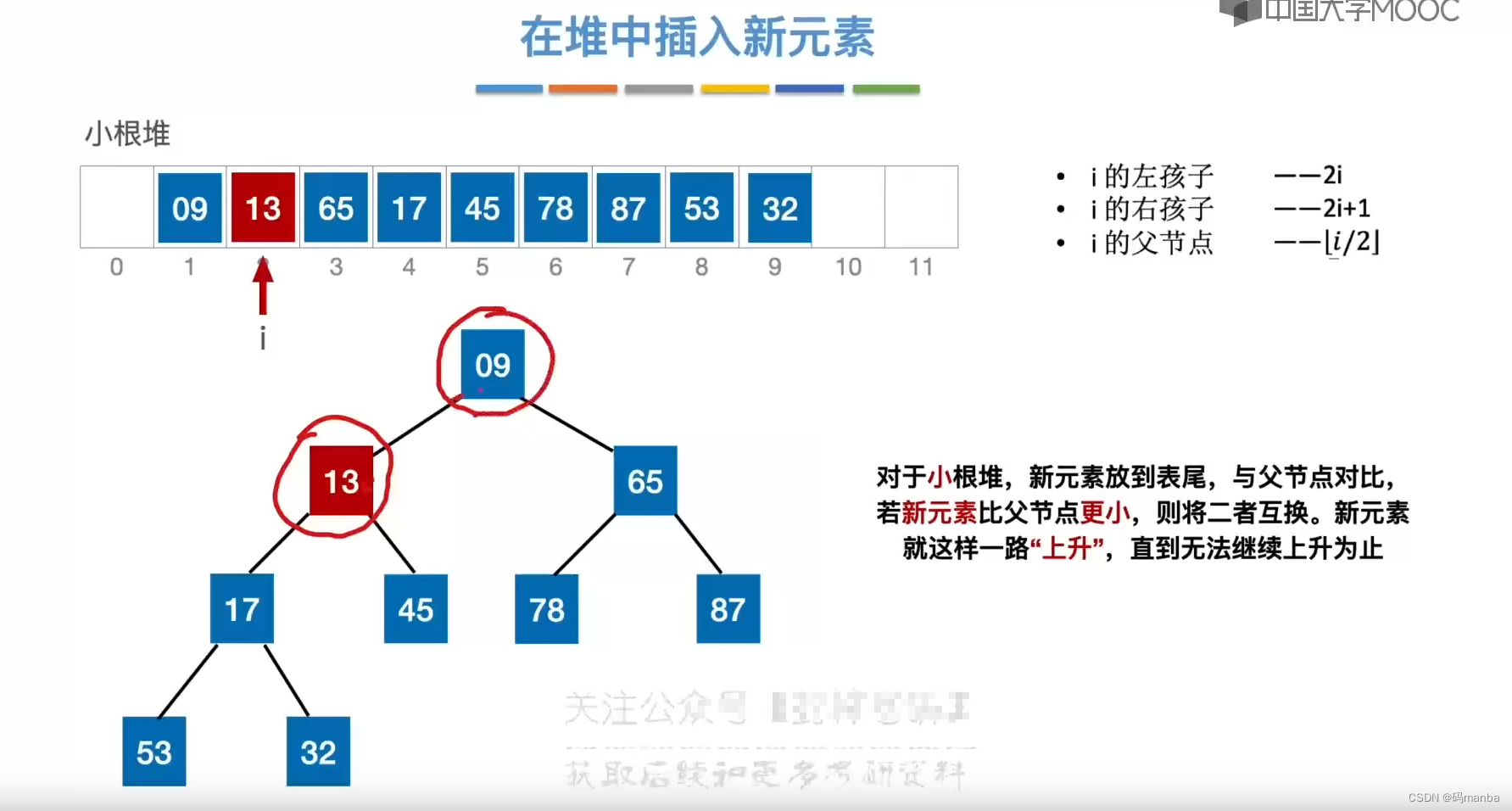
在小根堆中删除元素
- 1.首先删除对应元素,用堆底元素代替被删除的元素
- 2.然后让该元素一直与其孩子结点对比, 因为是小根堆,所以与更小的孩子换。
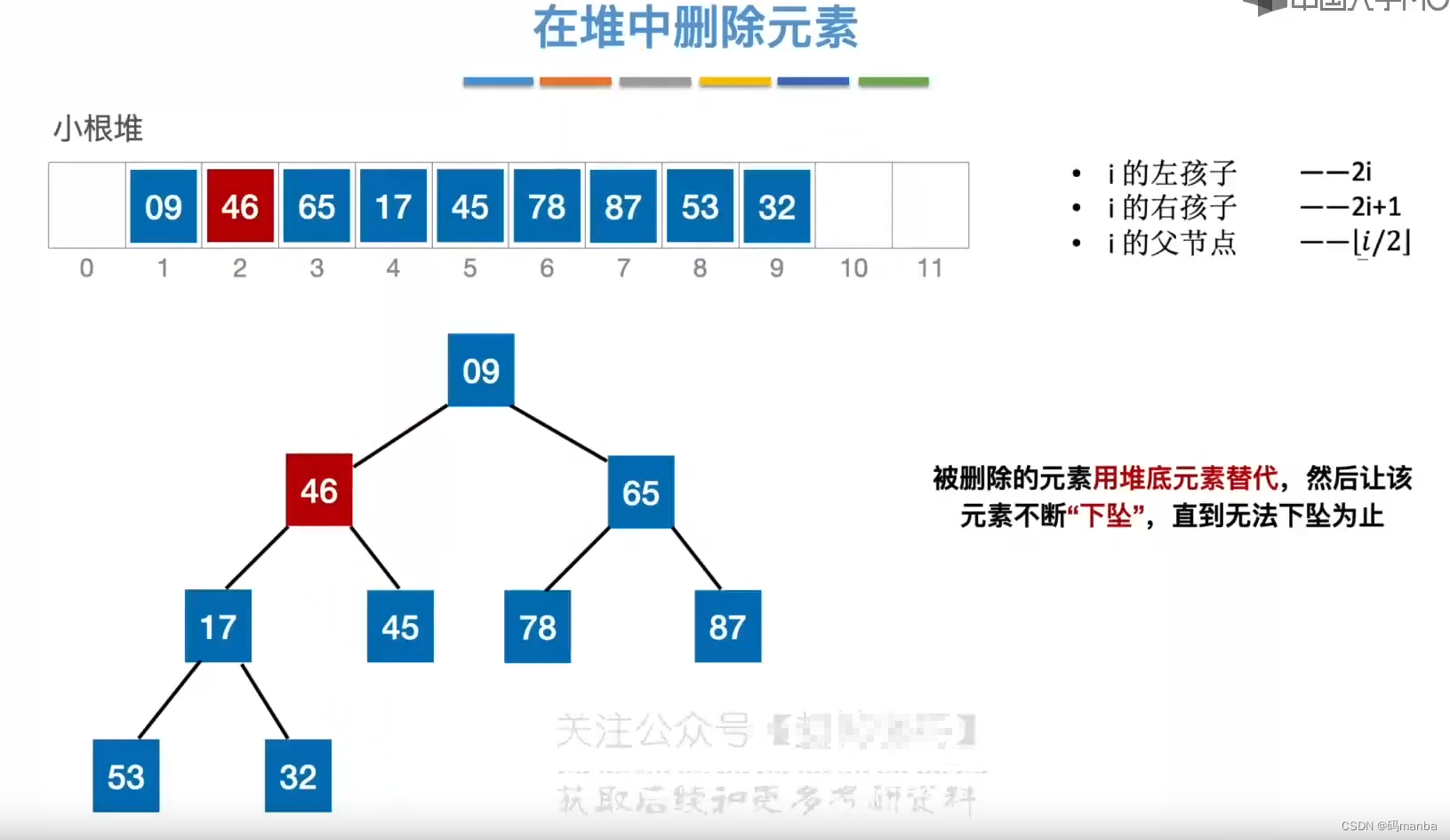
下坠过程中关键字对比过程
- 有几个孩子就对比几次
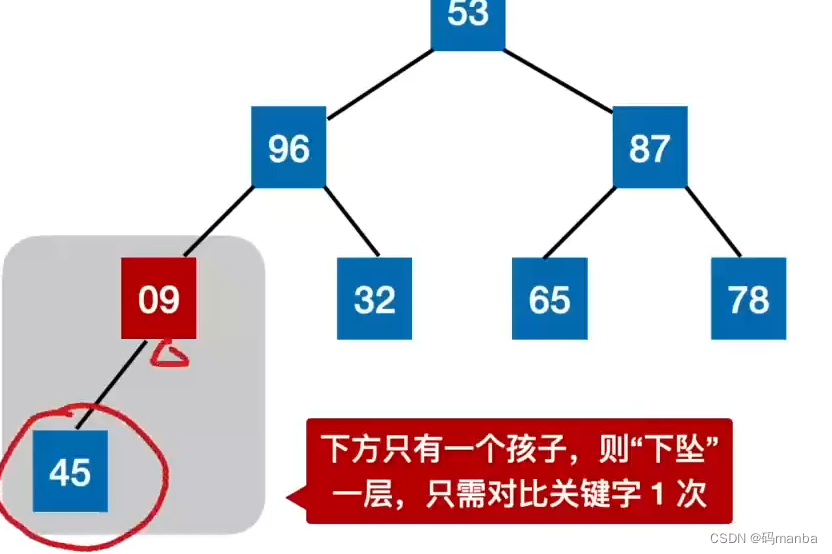
插入删除知识总结

五、归并排序与基数排序
5.1 归并排序
归并排序的介绍
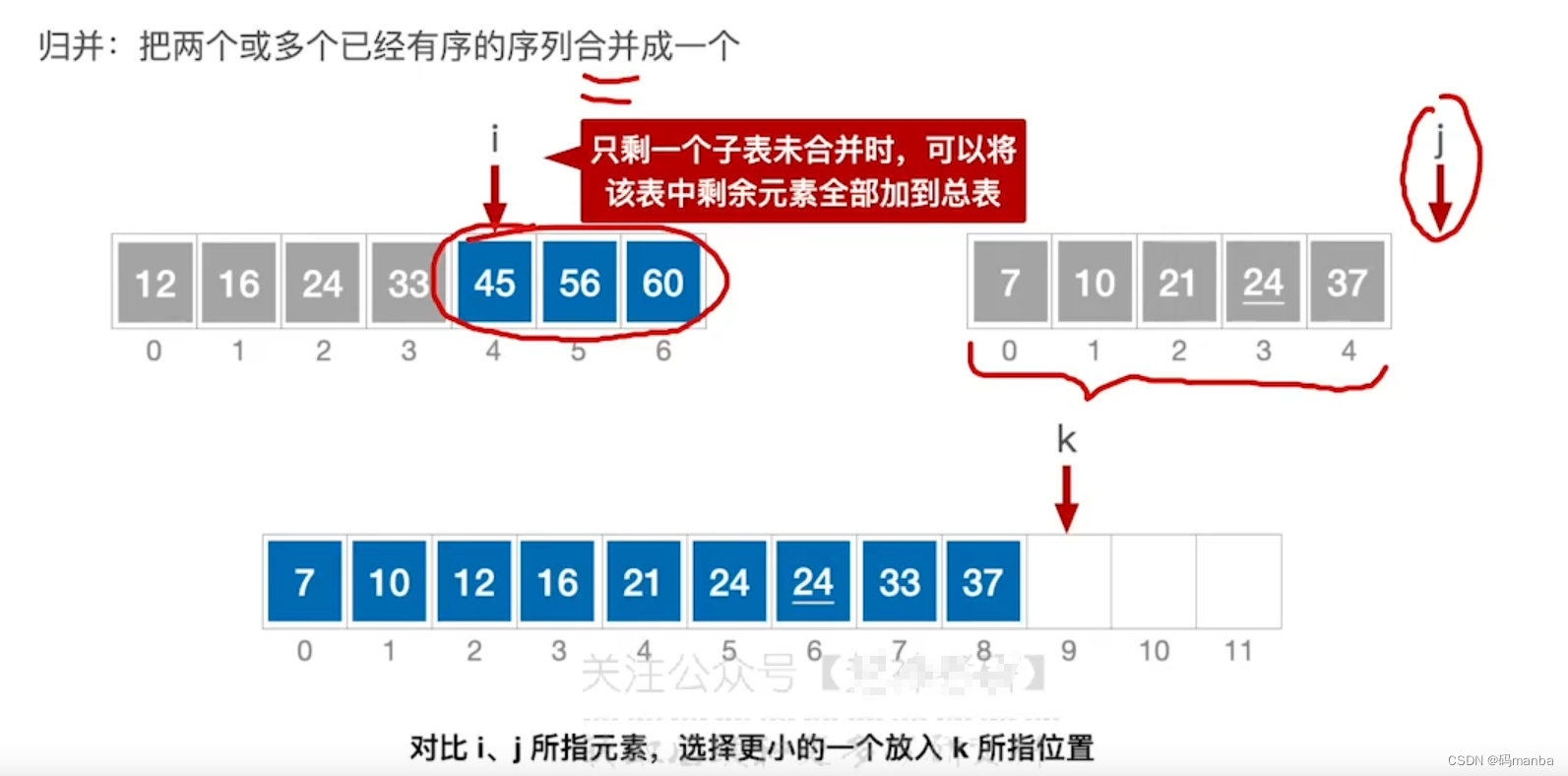
n路归并
- 几个有序数组就是几路归并
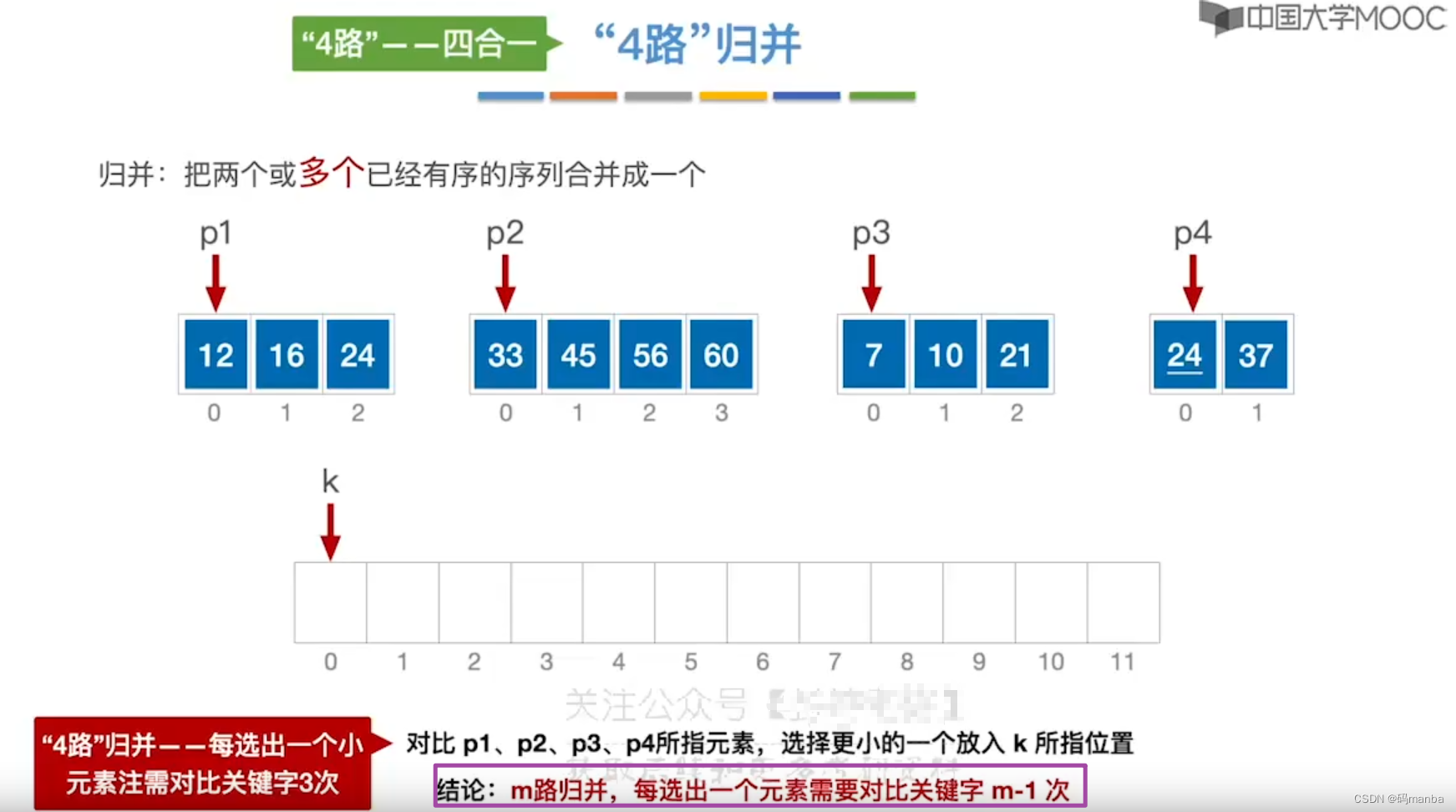
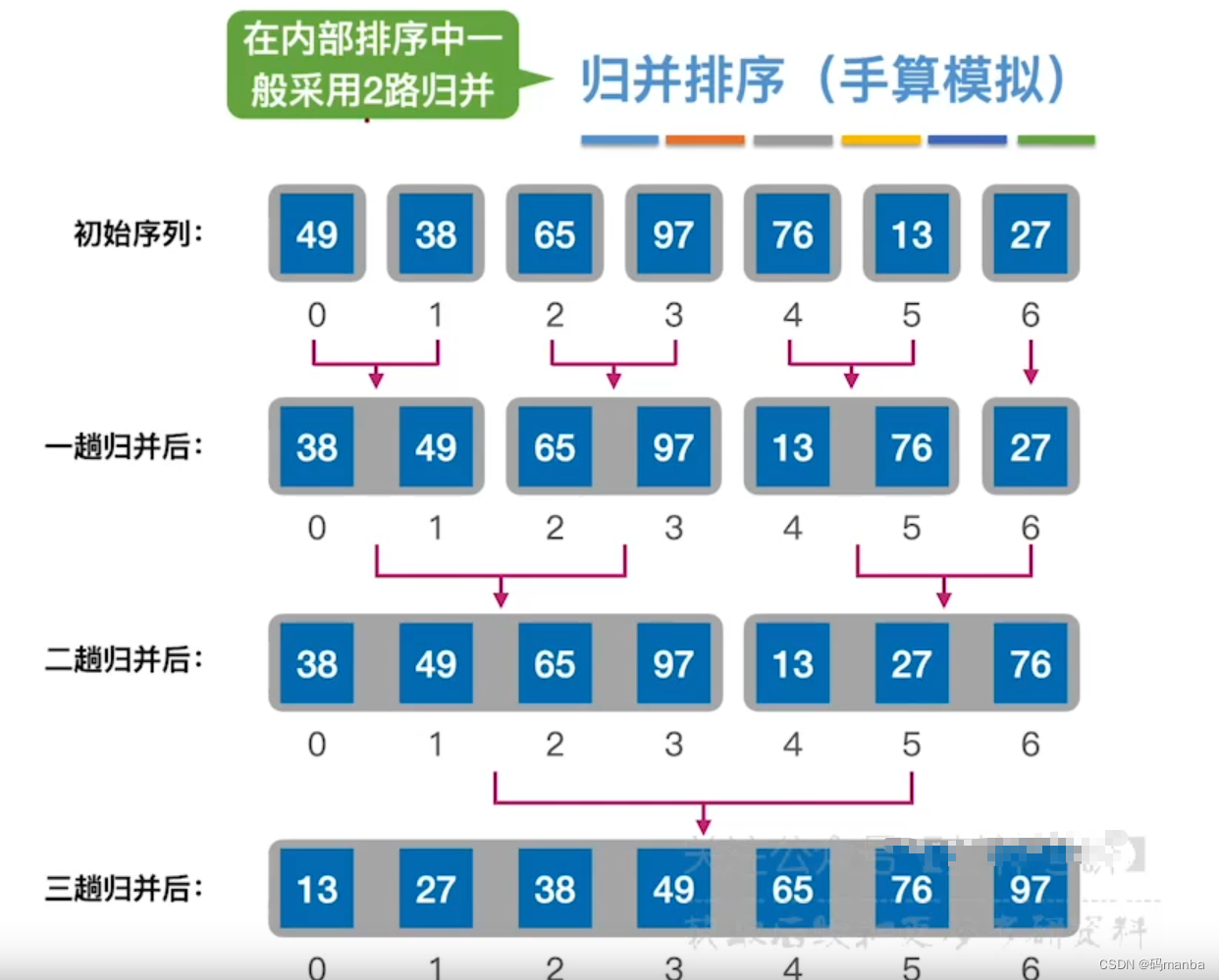
归并排序的具体思想
- 第一次归并其实 就是 两两进行归并
- 第二次归并,将上一趟归并好的,再两两归并。
- 依次执行,直到归并成一个有序的序列;
归并排序算法实现
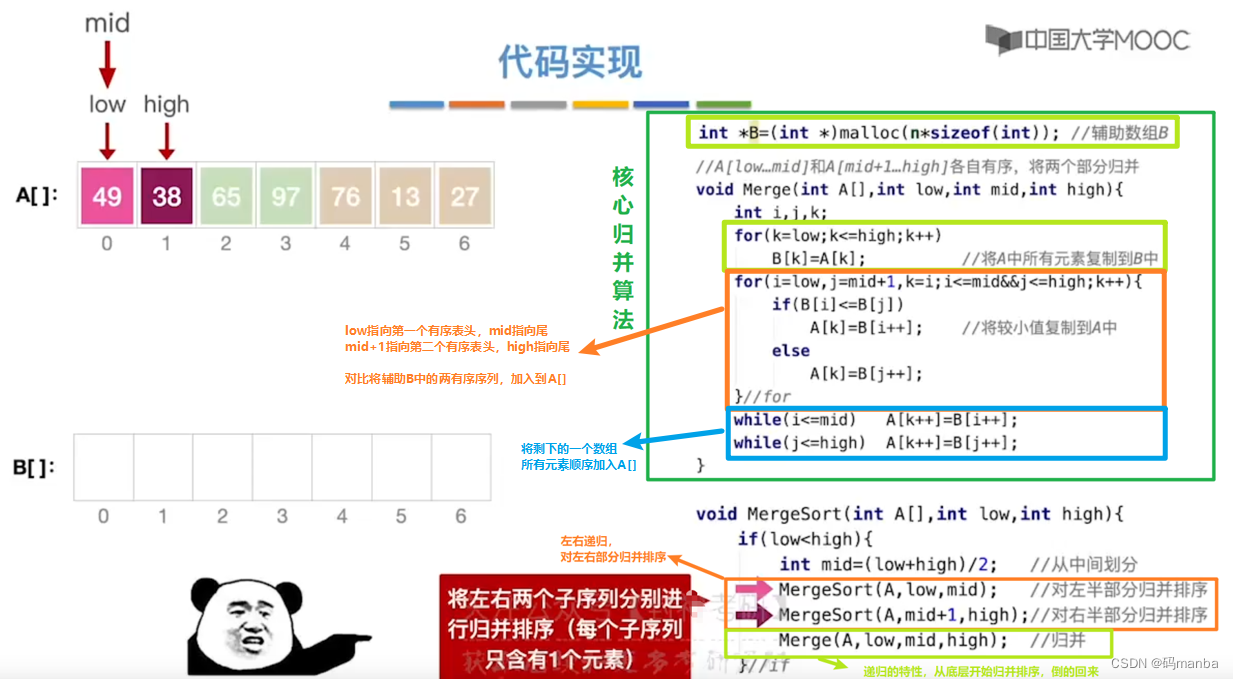
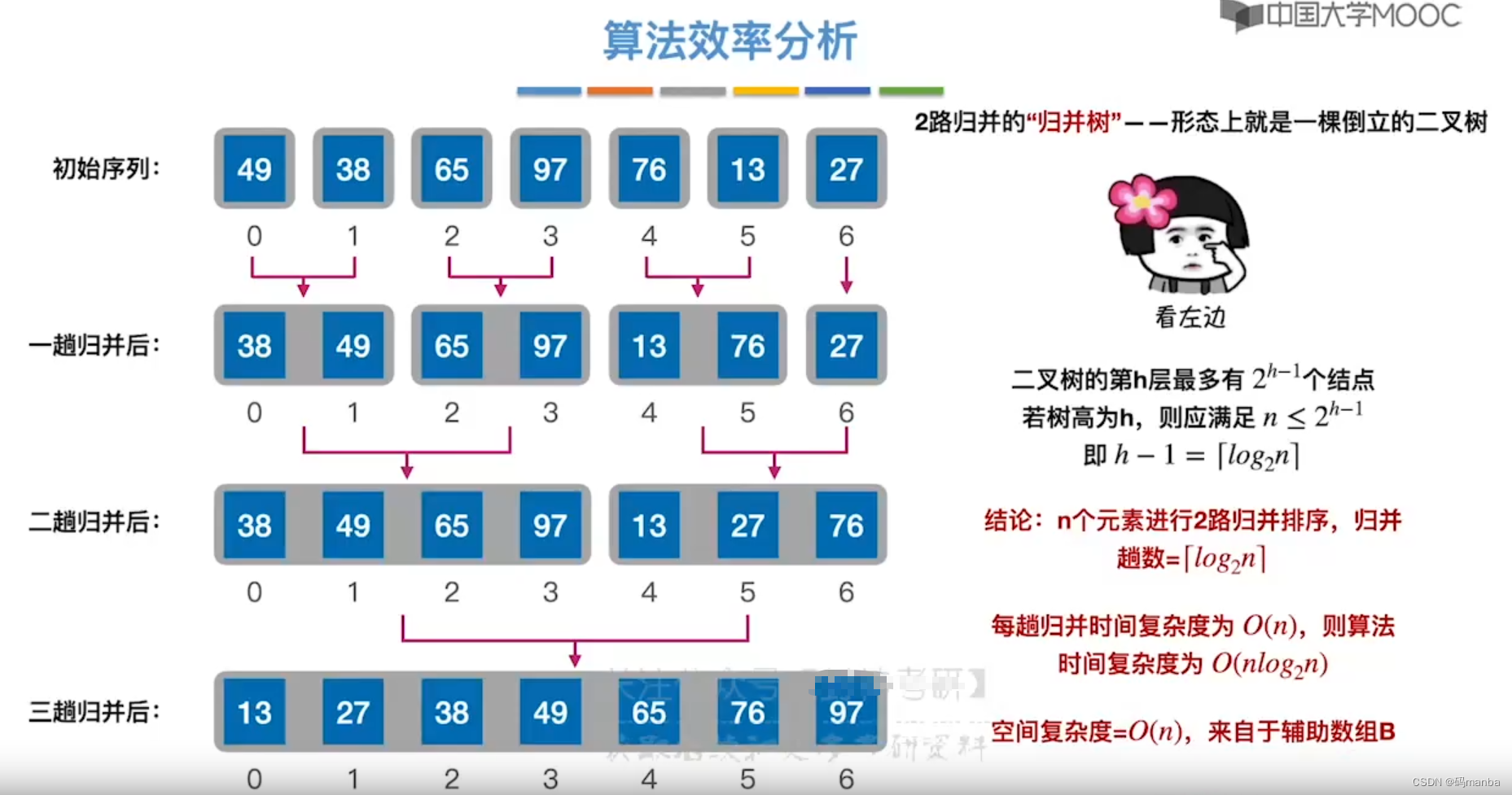
归并排序的时间效率分析
- 时间、空间复杂度如下
- 稳定性:稳定!
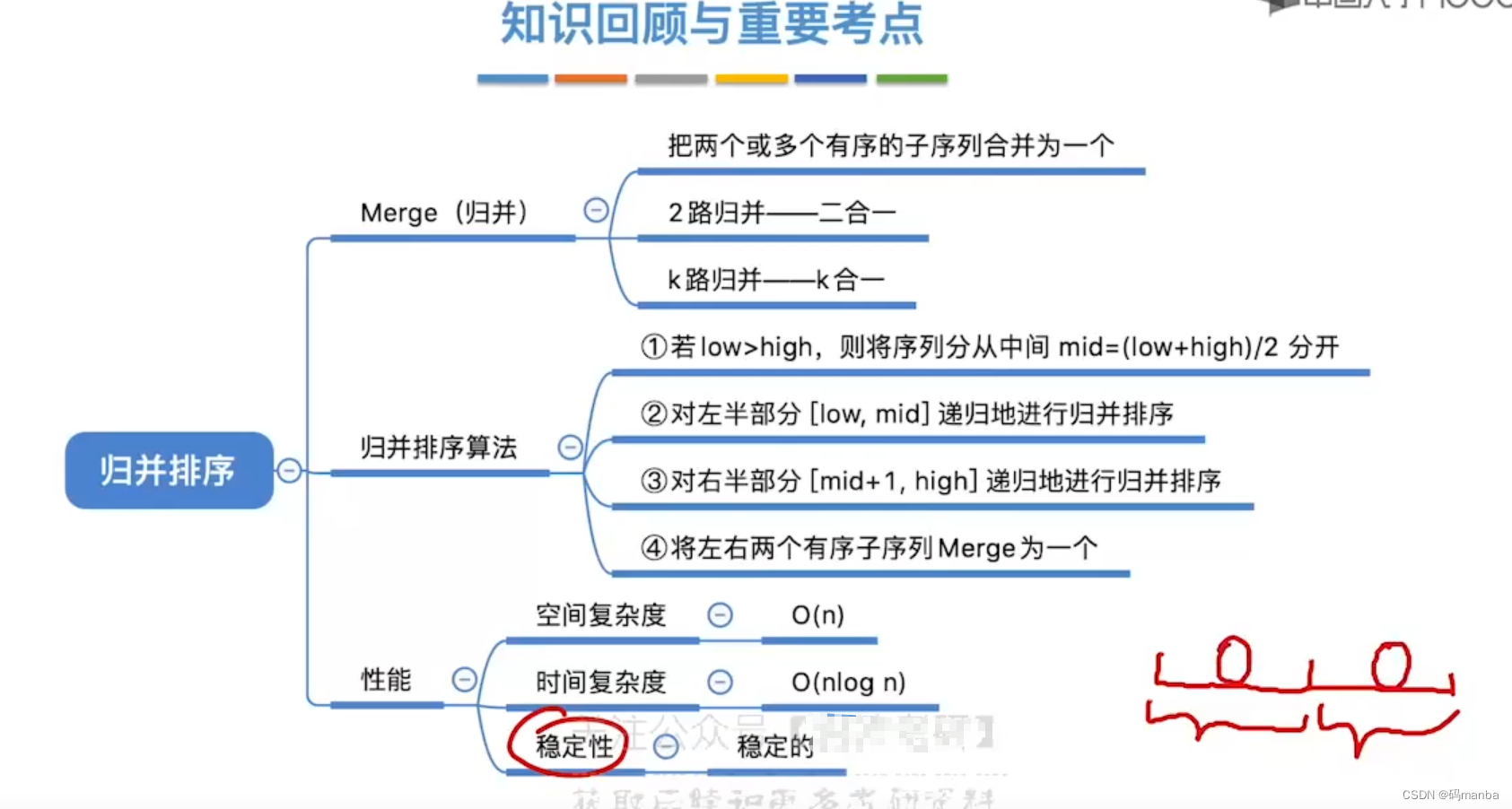
归并排序的知识总结
5.2 基数排序
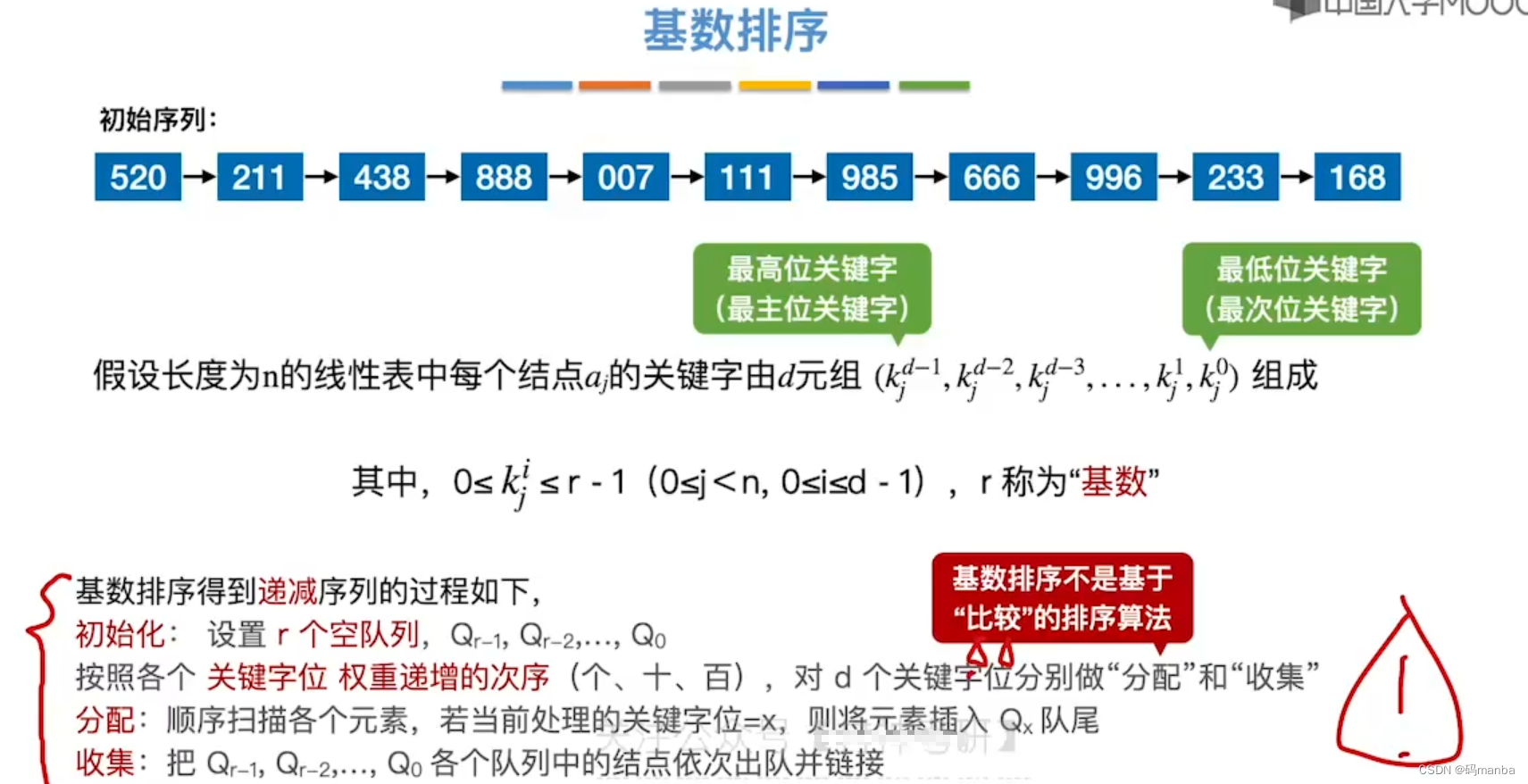
基数排序的执行步骤
- 建辅助队列数组
- 第一趟按个位进行分配
得到如此分布
第一趟收集结束后是按个位递减
3. 第二趟以十位进行分配
因为我们第一趟以个位分配,所以当十位相同时,个位越大的先入队了
第二趟收集后
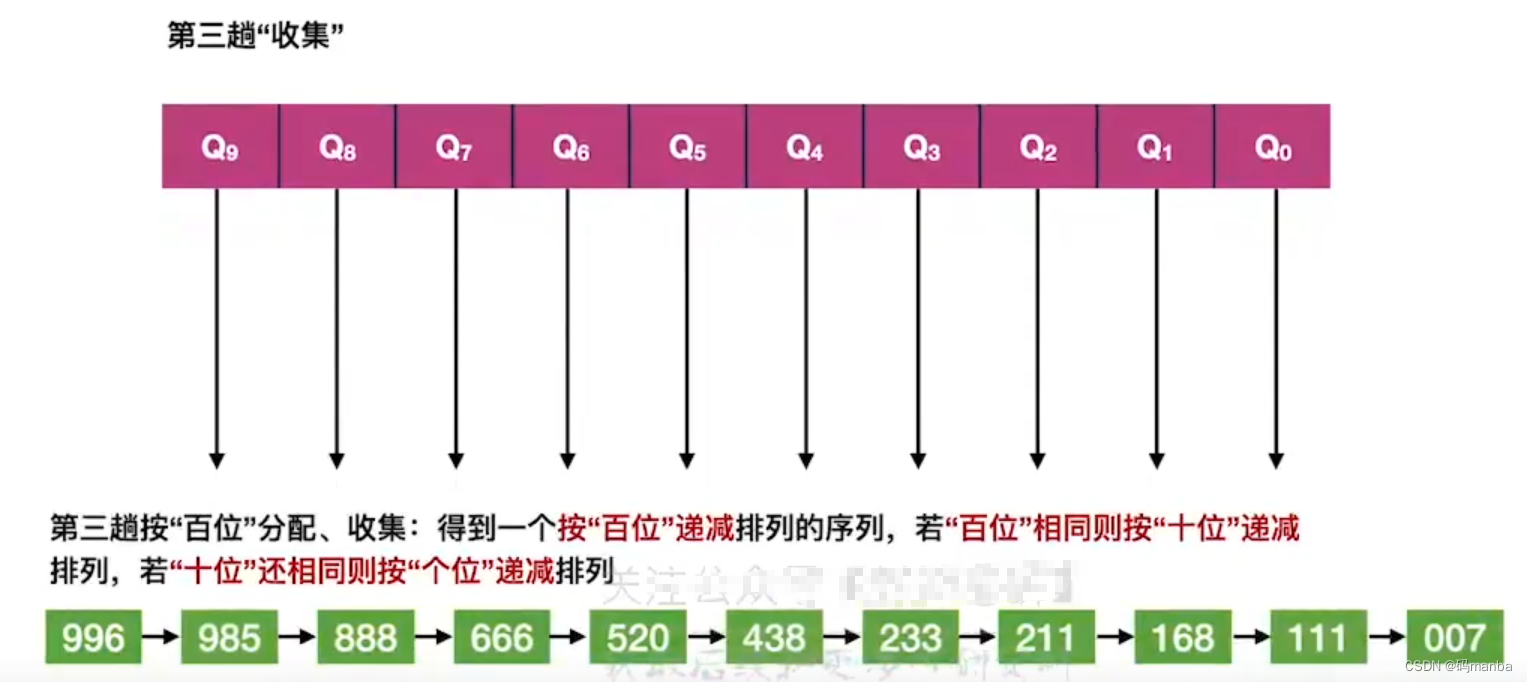
4. 第三趟就以百位进行分配
因为第二趟是按十位进行分配所以当百位相同时,十位大的先分配了
第三趟收集结束后就是一个有序额序列了
?基数排序步骤总览
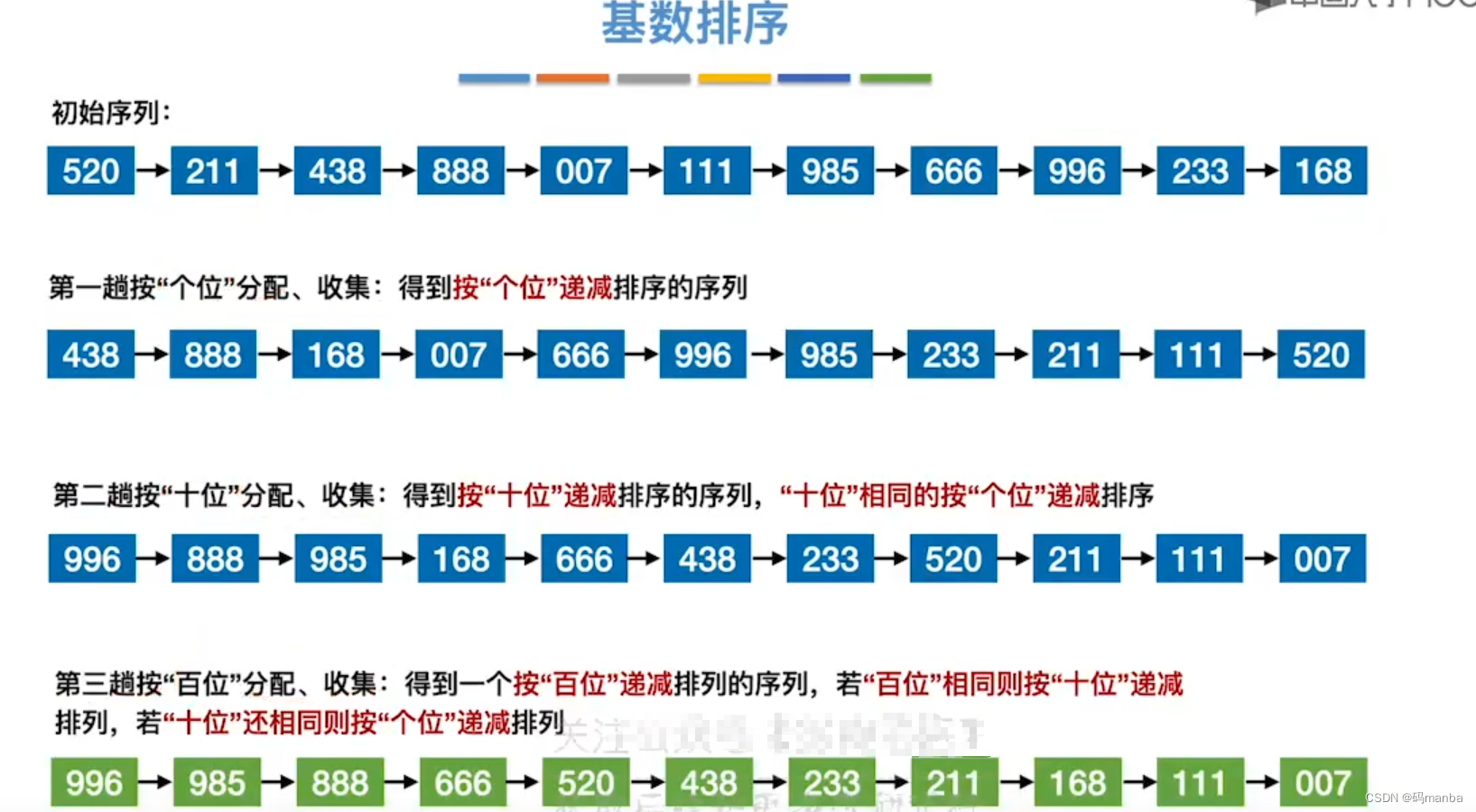
? 基数排序的文字描述
- 注意
- 如果递减的话 收集就从高位队列开始收集;
- 如果递增的话 收集就从低位队列开始收集;
- 基数排序并不是基于比较的排序;
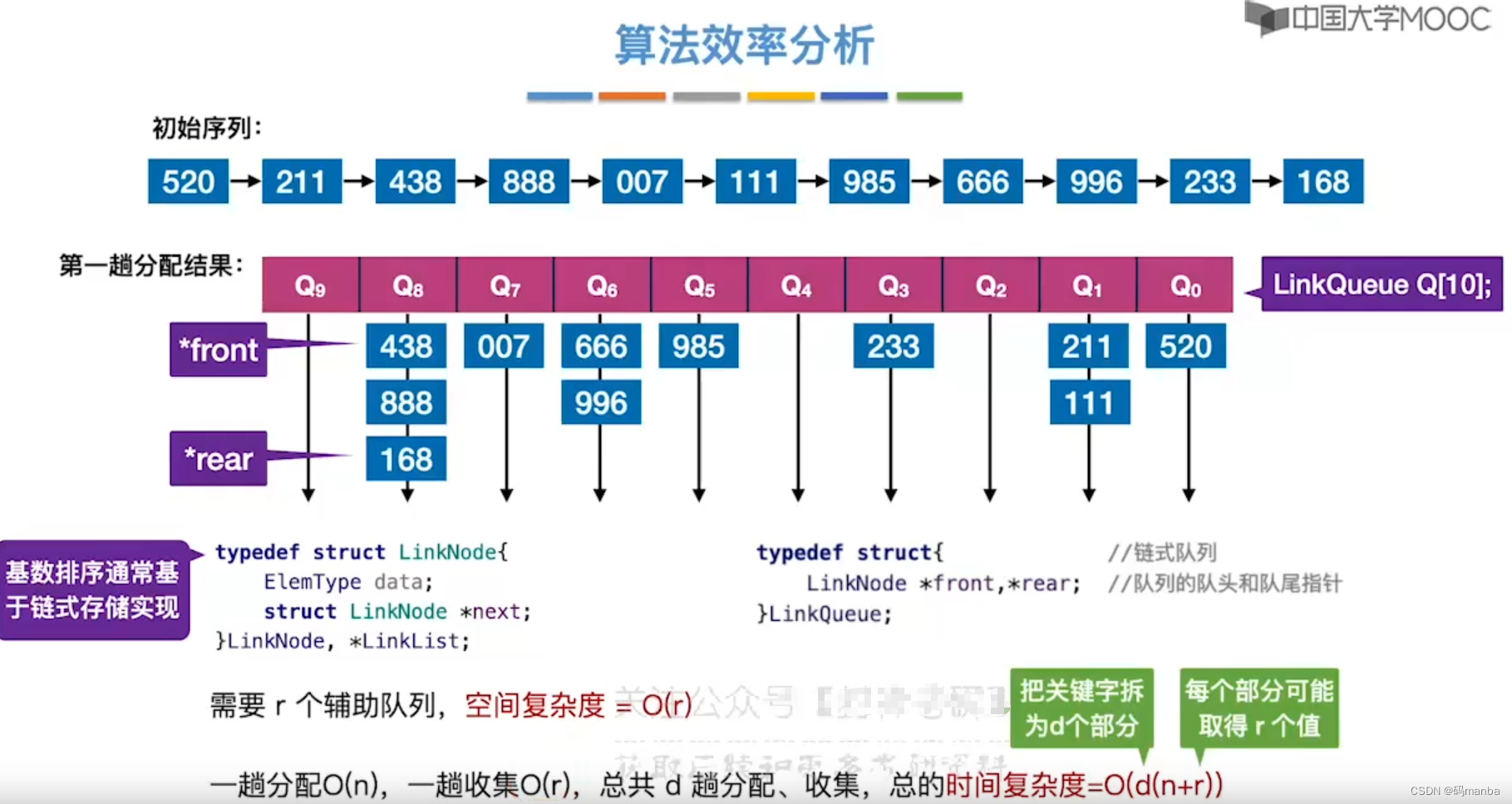
时间效率分析
- 时间、空间复杂度
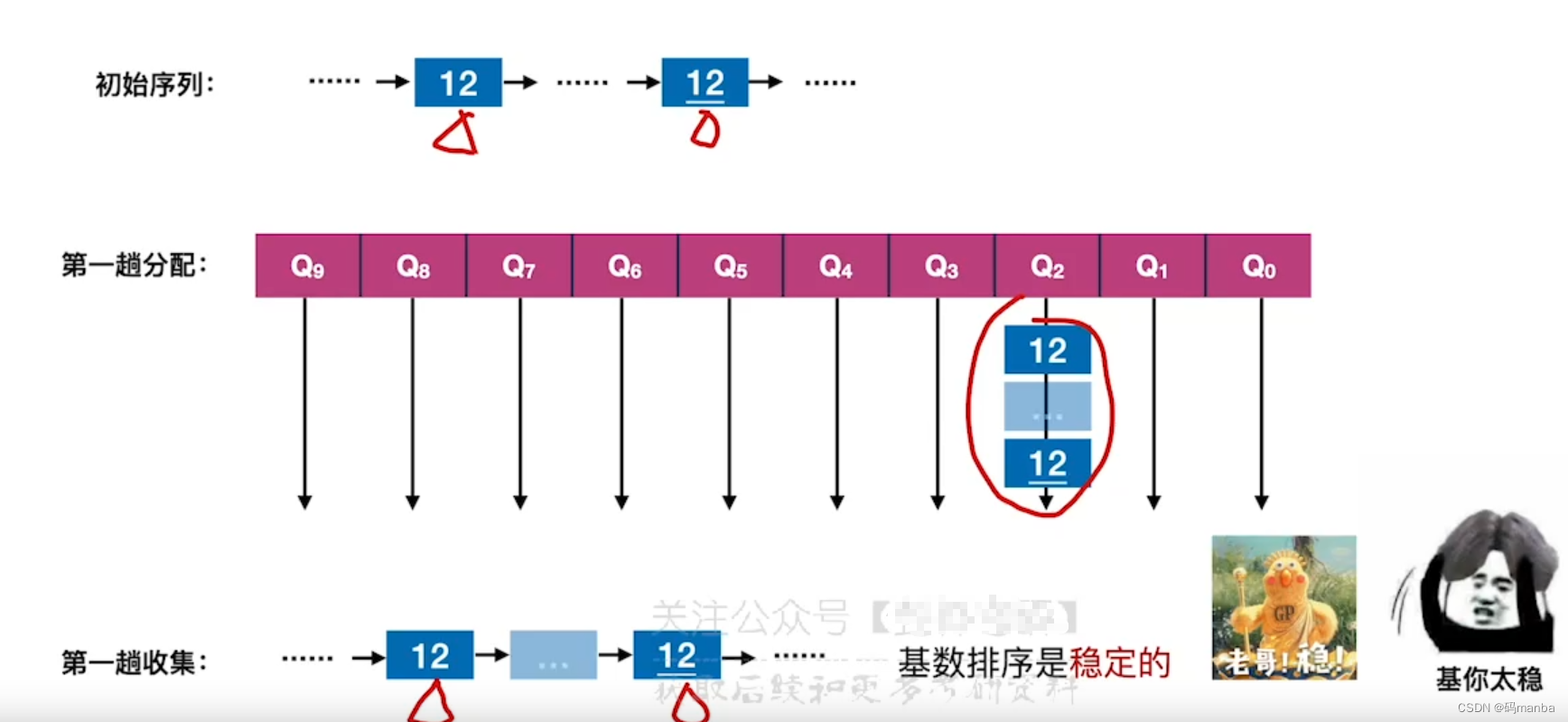
- 稳定性
基数排序的应用
? 年龄排序
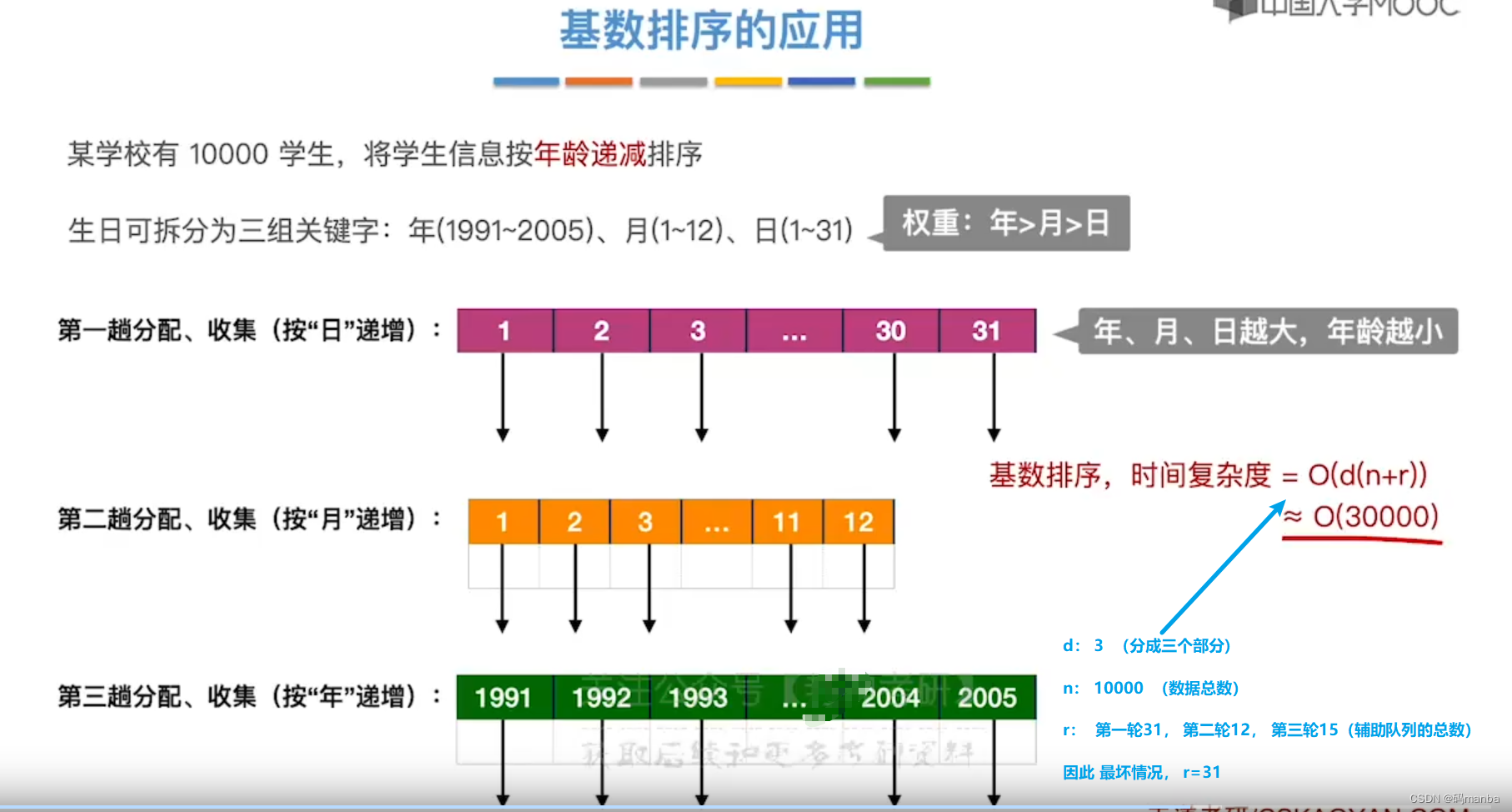
? 基数排序善于解决什么问题?

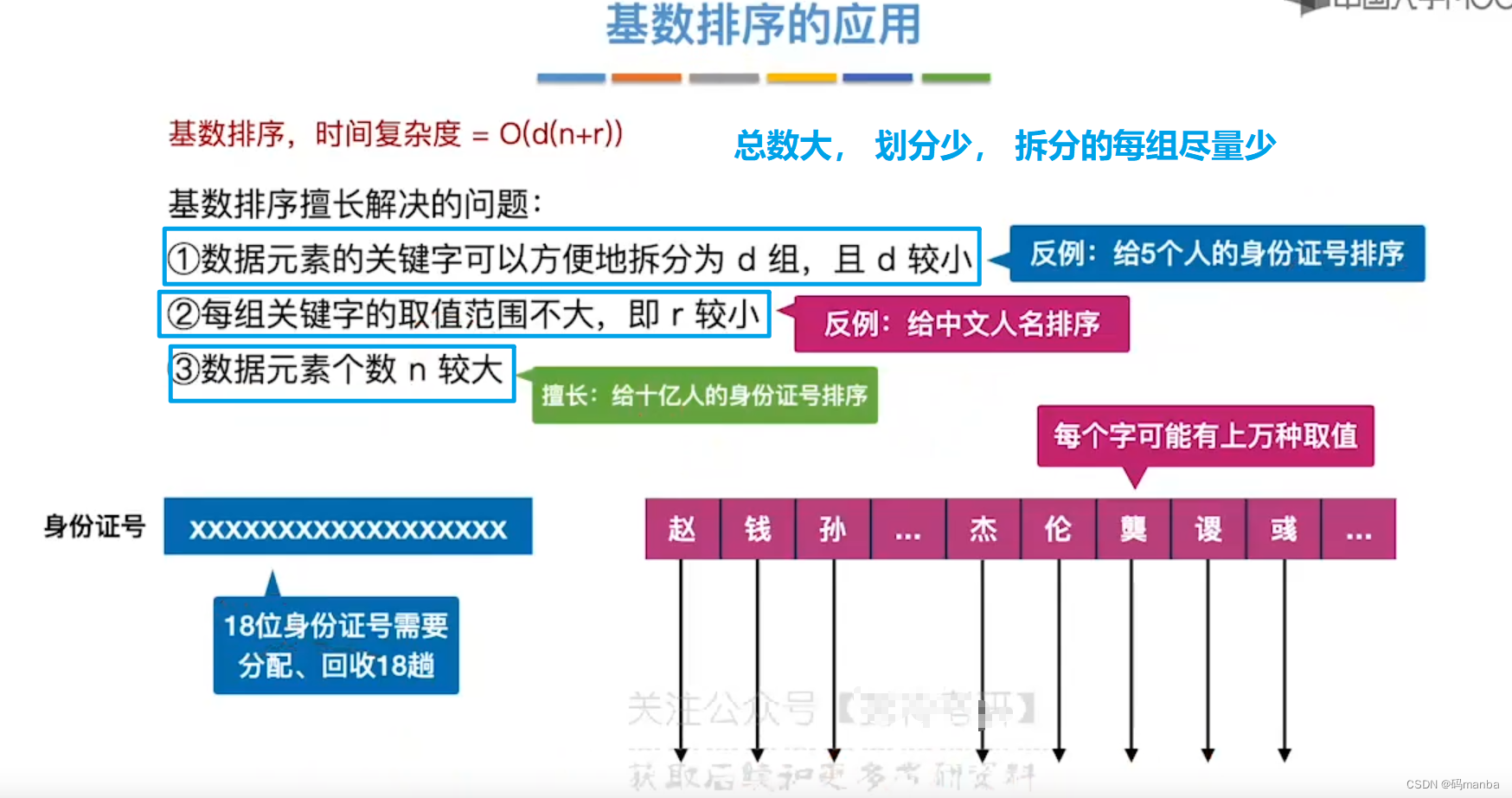
基数排序知识总结

六、 内部排序算法大对比
6.1 从时空复杂度、稳定性、算法过程特征分析


6.2 各种算法的时间复杂度、空间复杂度、稳定性整理
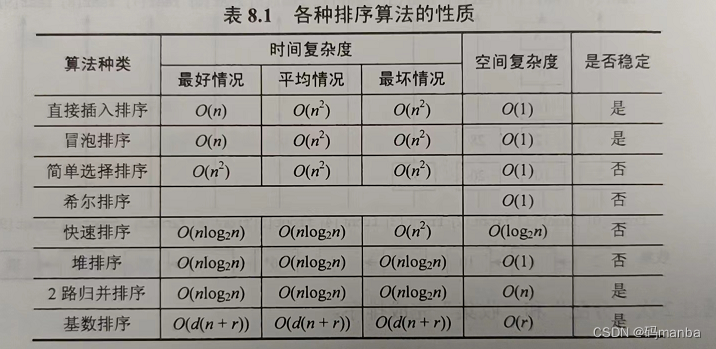
6.3 对内部排序算法比较和应用考虑的情况


七、 外部排序
7.1 外存、内存之间的数据交换
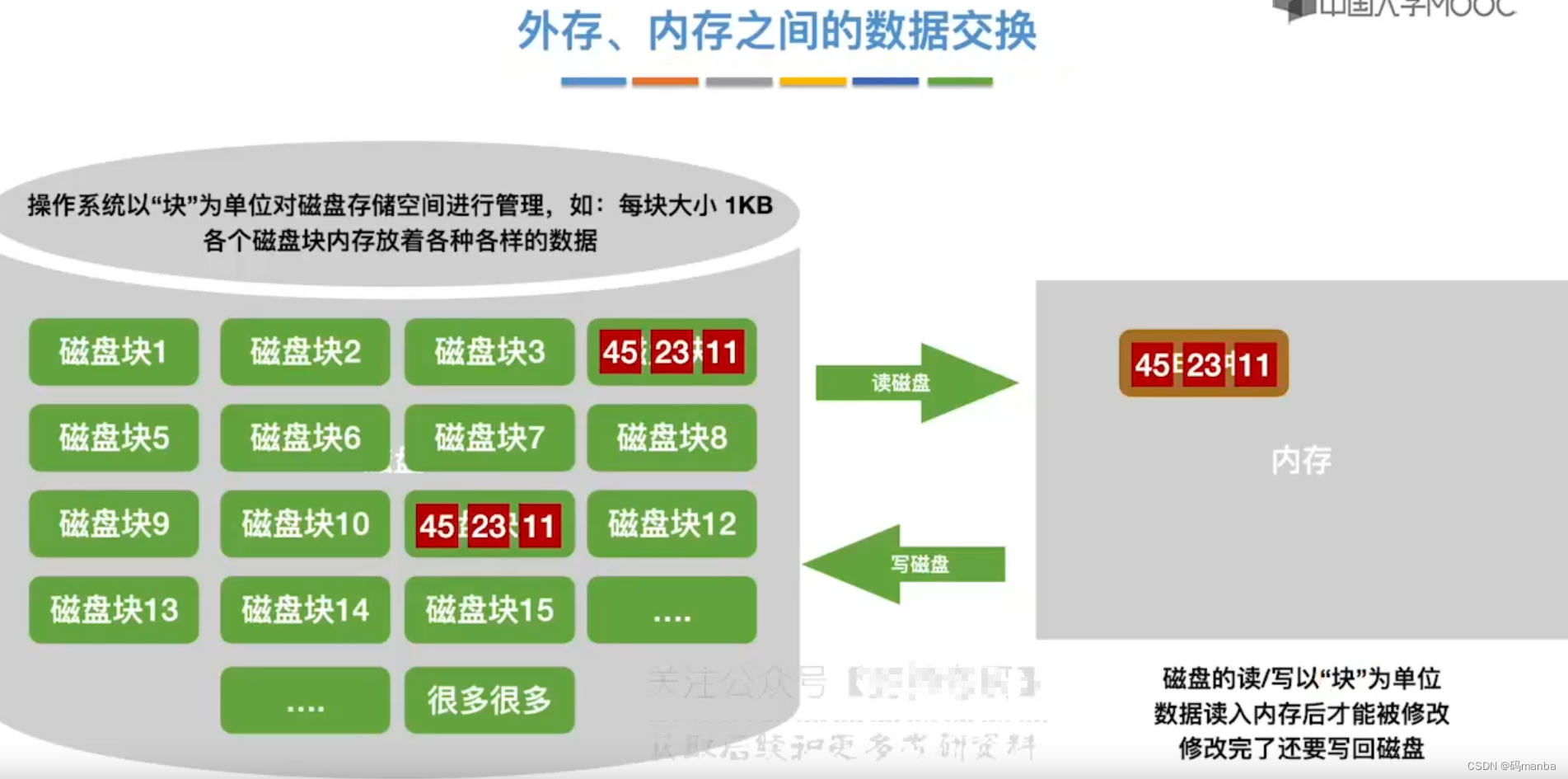
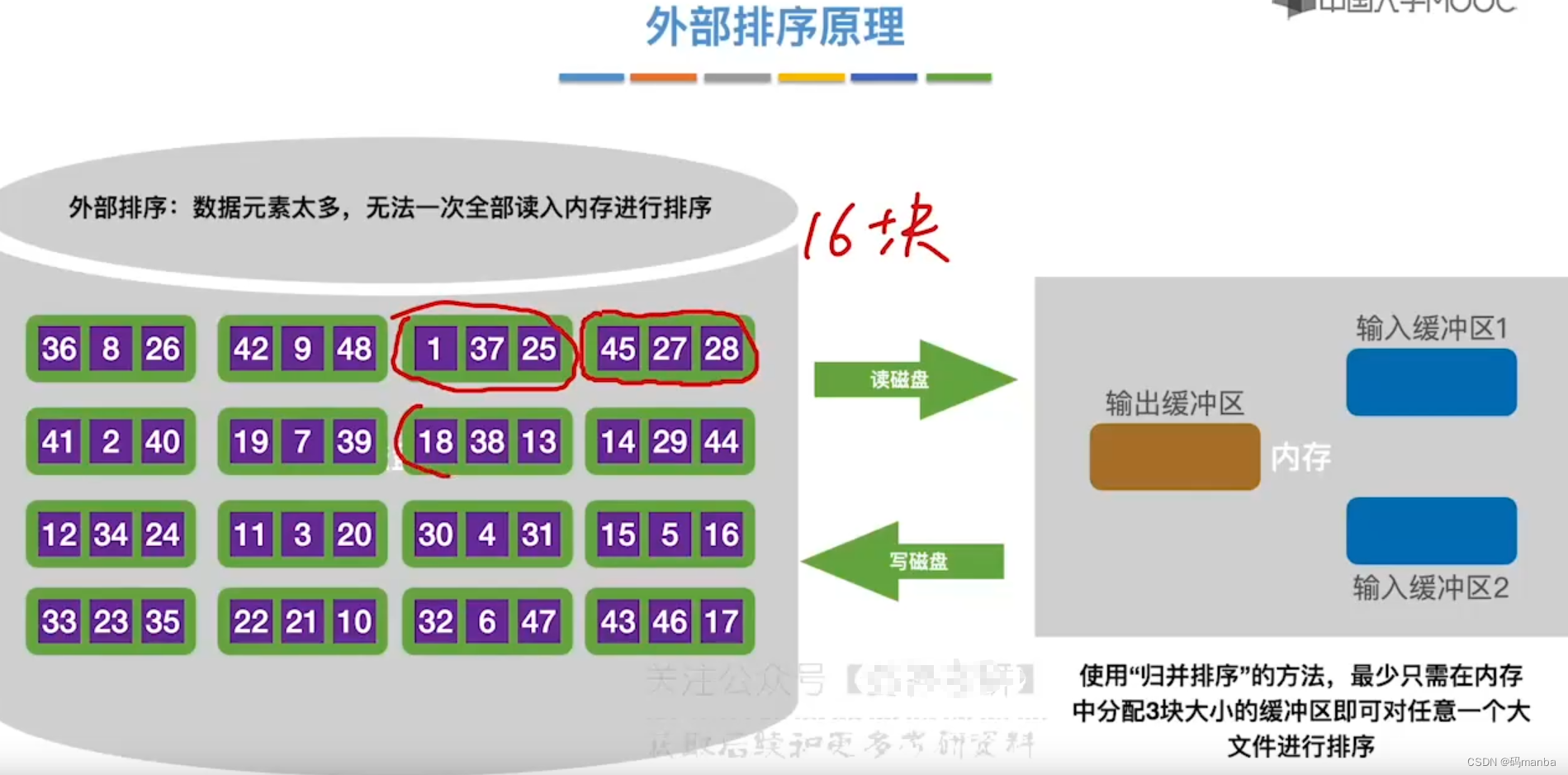
7.2 外部排序的原理
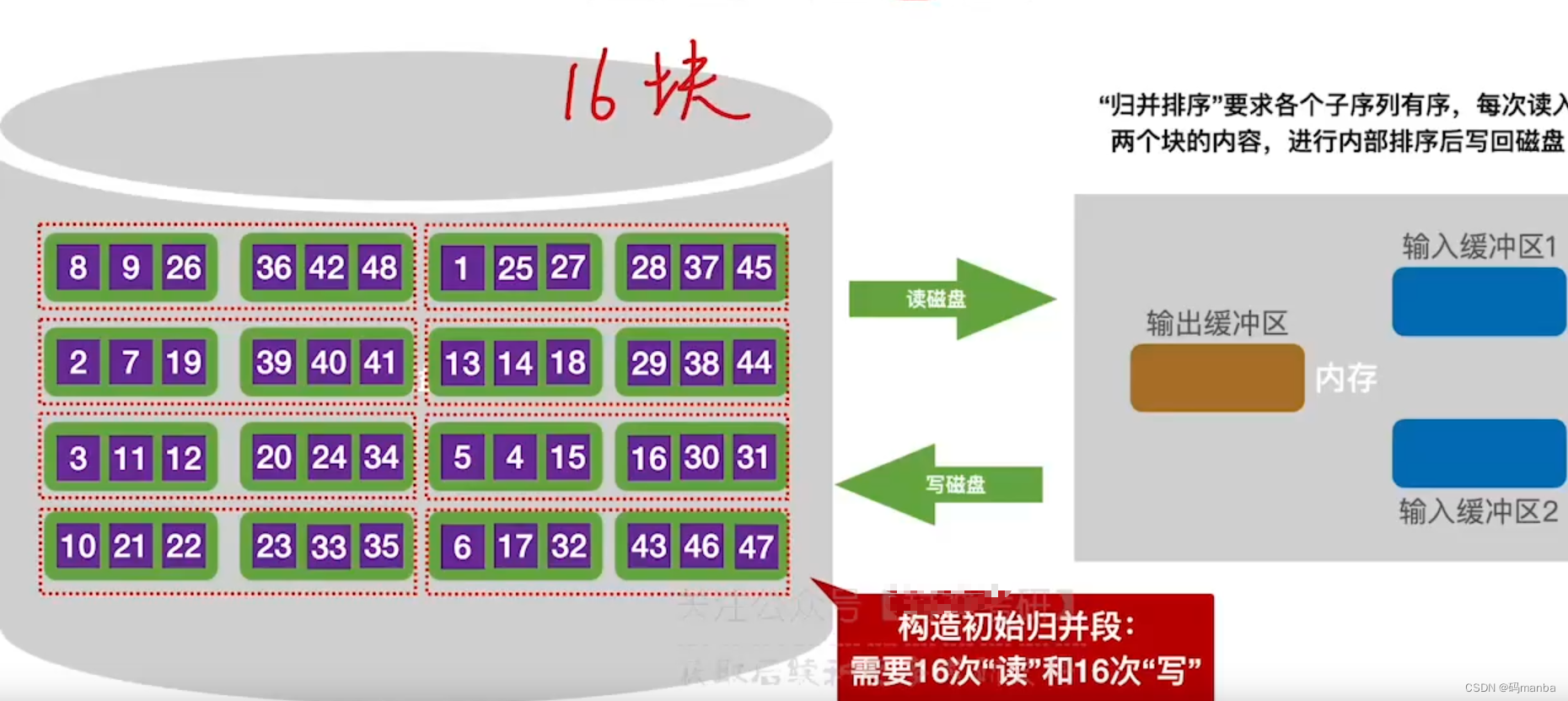
- 只需要三块大小的缓冲区(两个输入,一个输出)即可对任意的文件进行排序。
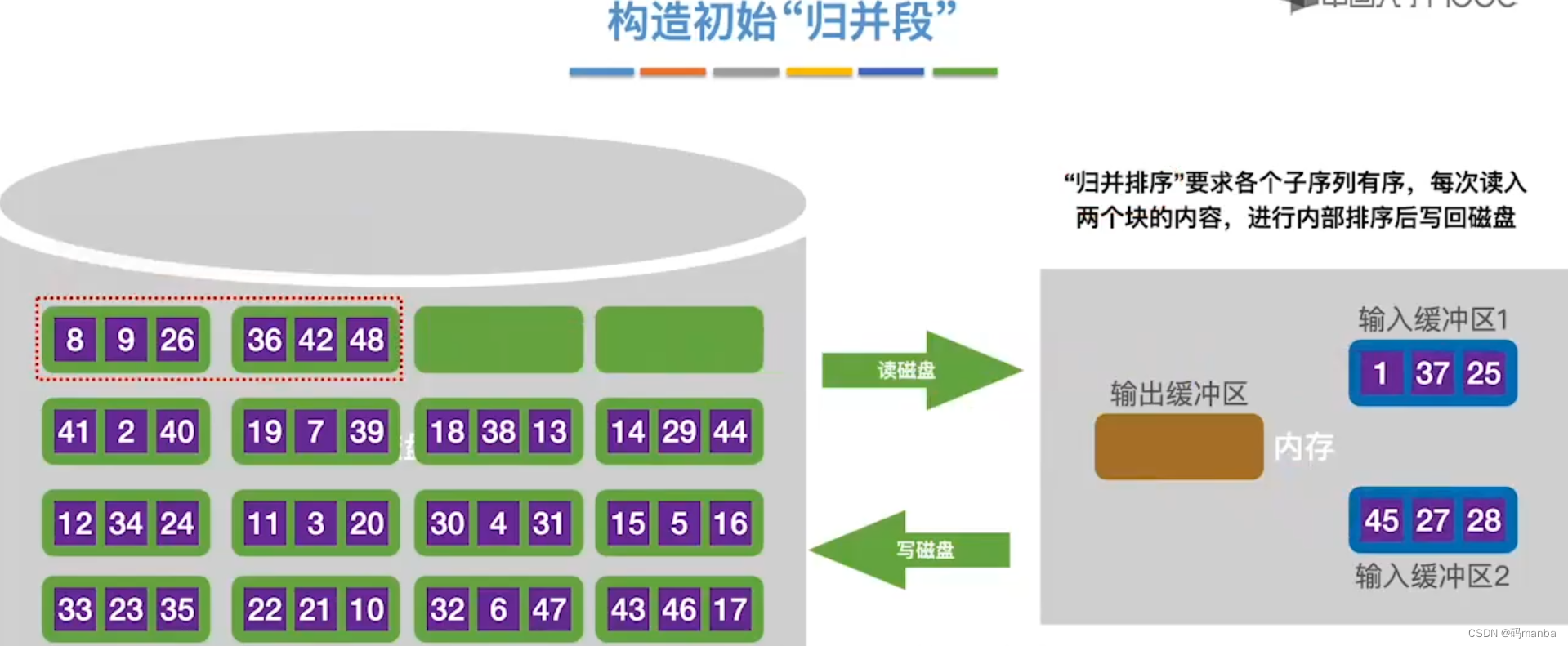
- 构造初始归并块
- 每次读入两个块到内存的两个输入缓冲区 ,进行内部排序;
- 排好序的块,通过输出缓冲区,写回到磁盘;
n个块需要n次读、写操作;
🌙 进行“归并排序”
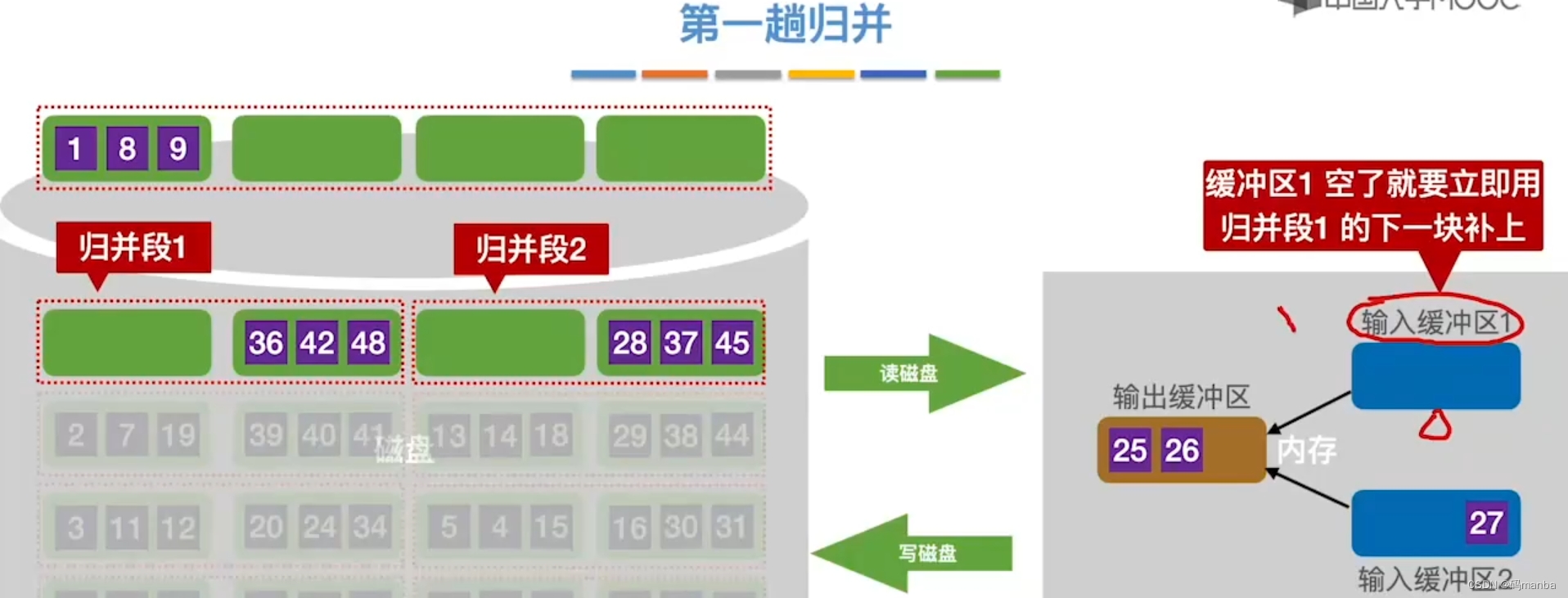
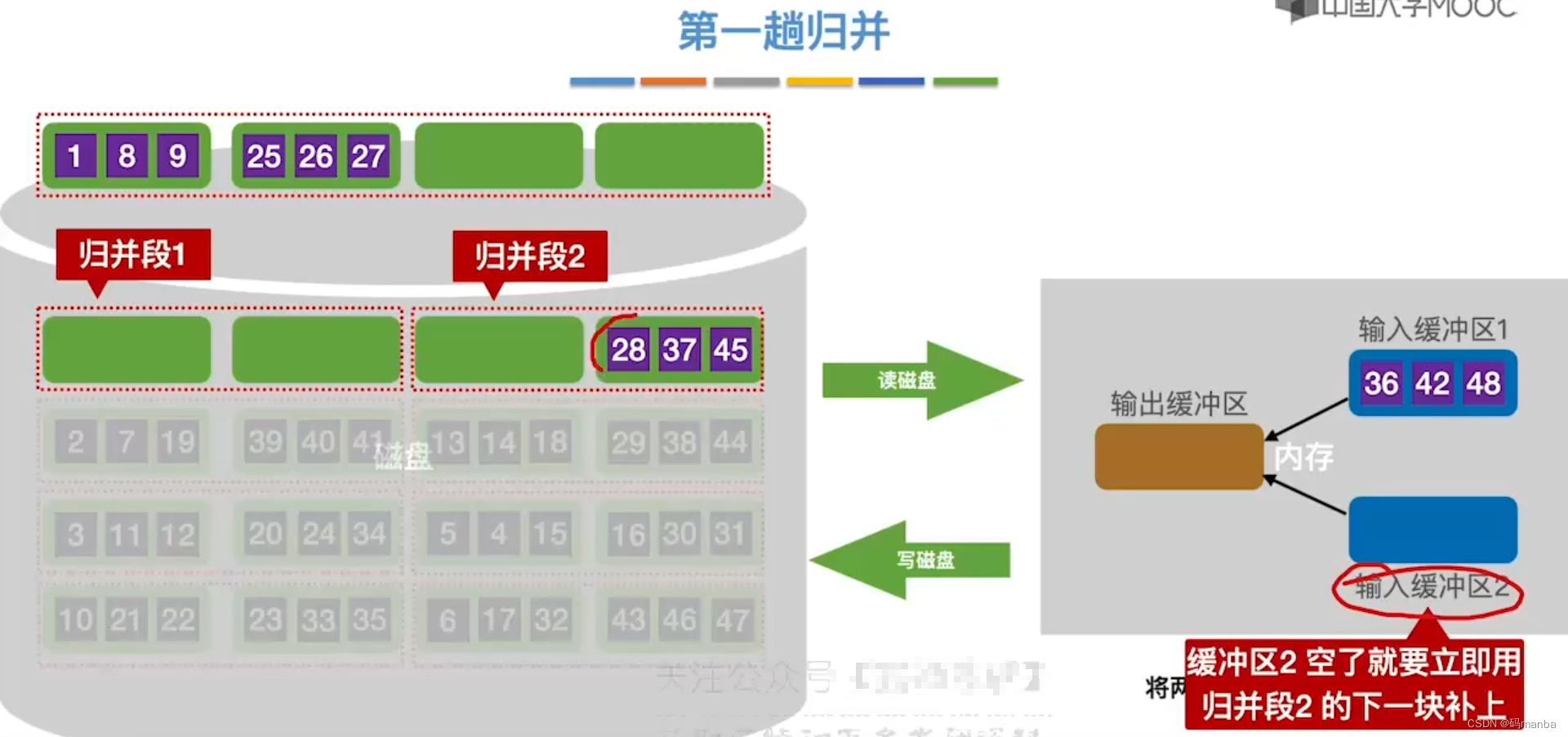
? 第一趟归并
- 假如一个归并段有两个块,在两个归并段中,读入两个最小的块到输入缓冲区,进行归并排序,存储到输出缓冲区;
2. 当输出缓冲区满了以后,将数据写出到外存;
当缓冲区空了后,接的读入数据。如果是输入缓冲区1读入的归并段1了,它空了就快速读入归并段1的后一块数据。如果输入缓冲区2空了,同理。
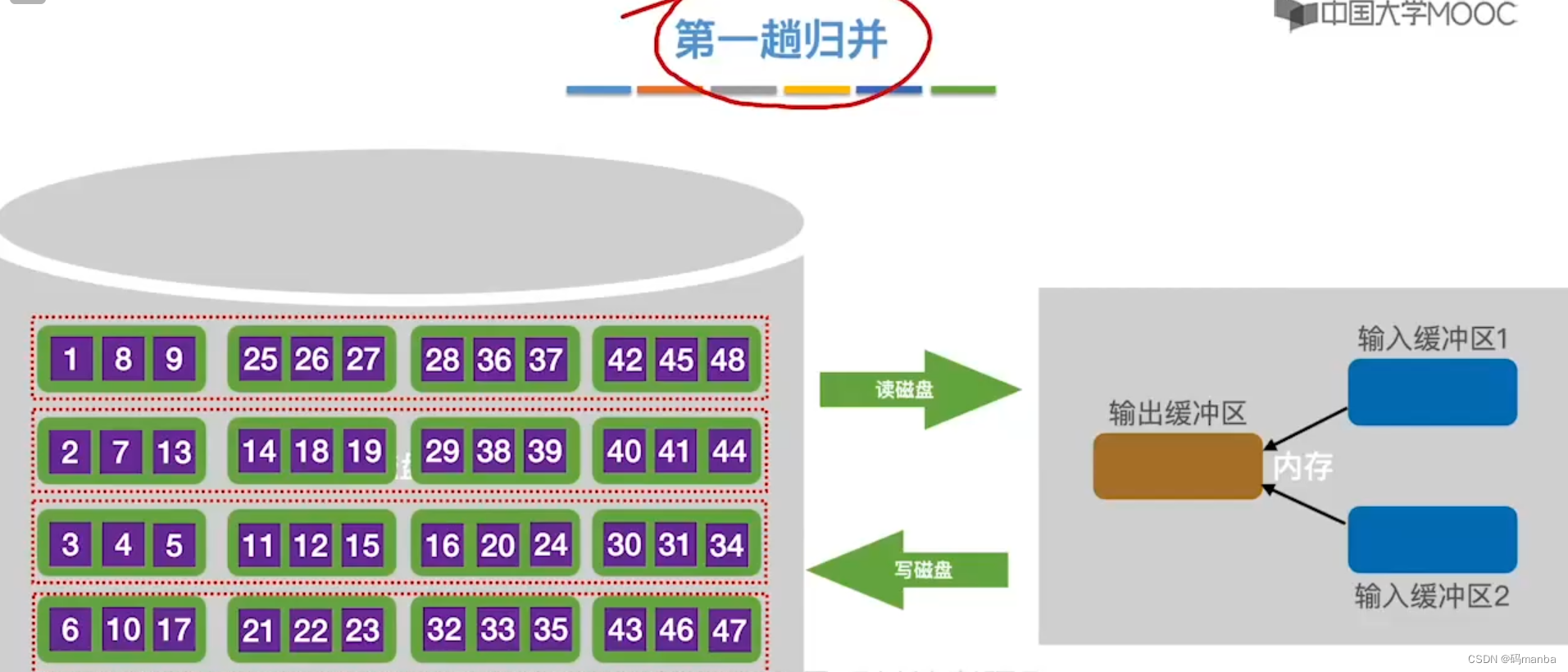
- 下面的归并段也是如此逻辑,第一趟归并结束后如图所示。
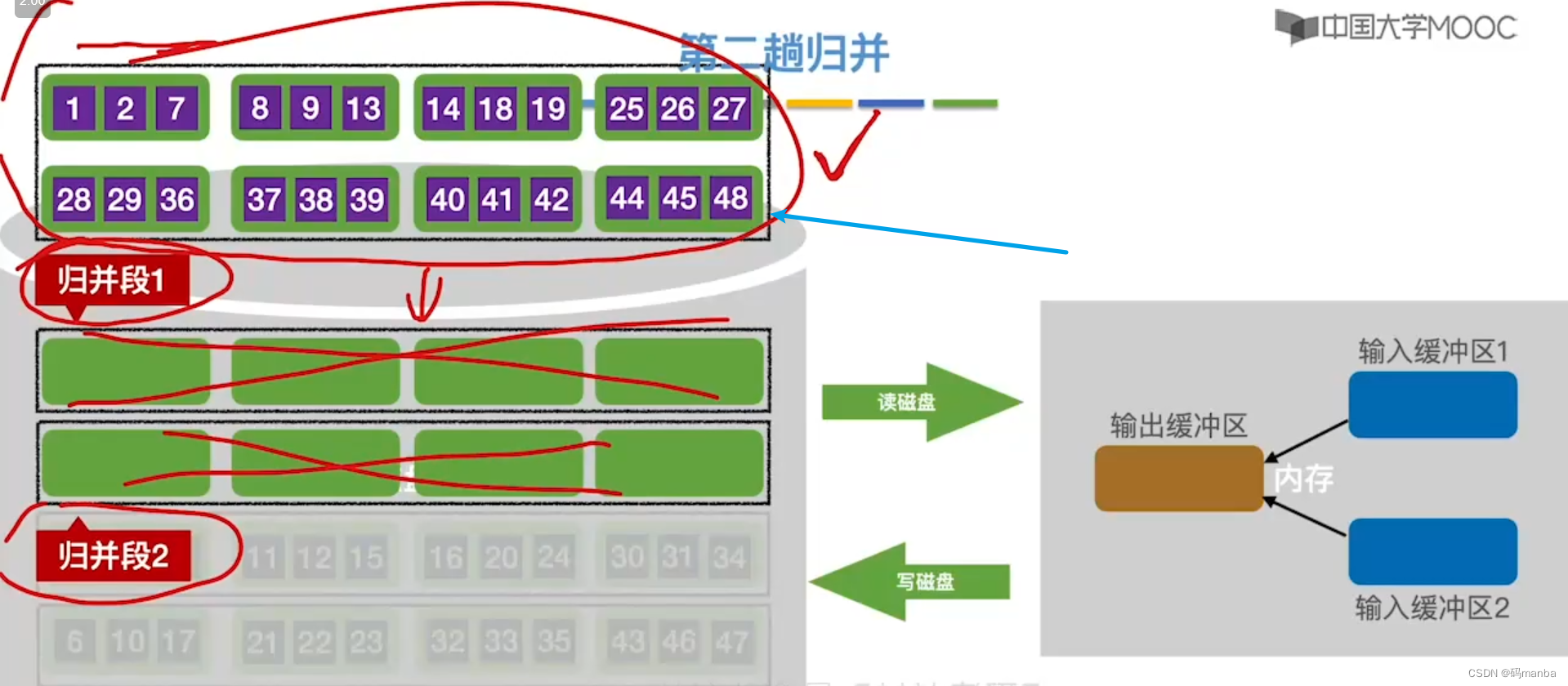
?第二趟归并
- 此时一个归并段有四个块,我们将两个归并段中最小的一块读进到输入缓冲区,进行归并排序,放到输出缓冲区。
- 输出缓冲区满了一块,就写到外存一块;
- 输入缓冲区空了,就从对应输送数据的归并块读入元素;
- 两个归并段全部排序完,再按此逻辑排序其他的归并块;
- 直到全部排序;
值得注意的是,每次归并完两块归并段,其实是存到外村的其他存储空间的,原来元素占用的存储空间归还。
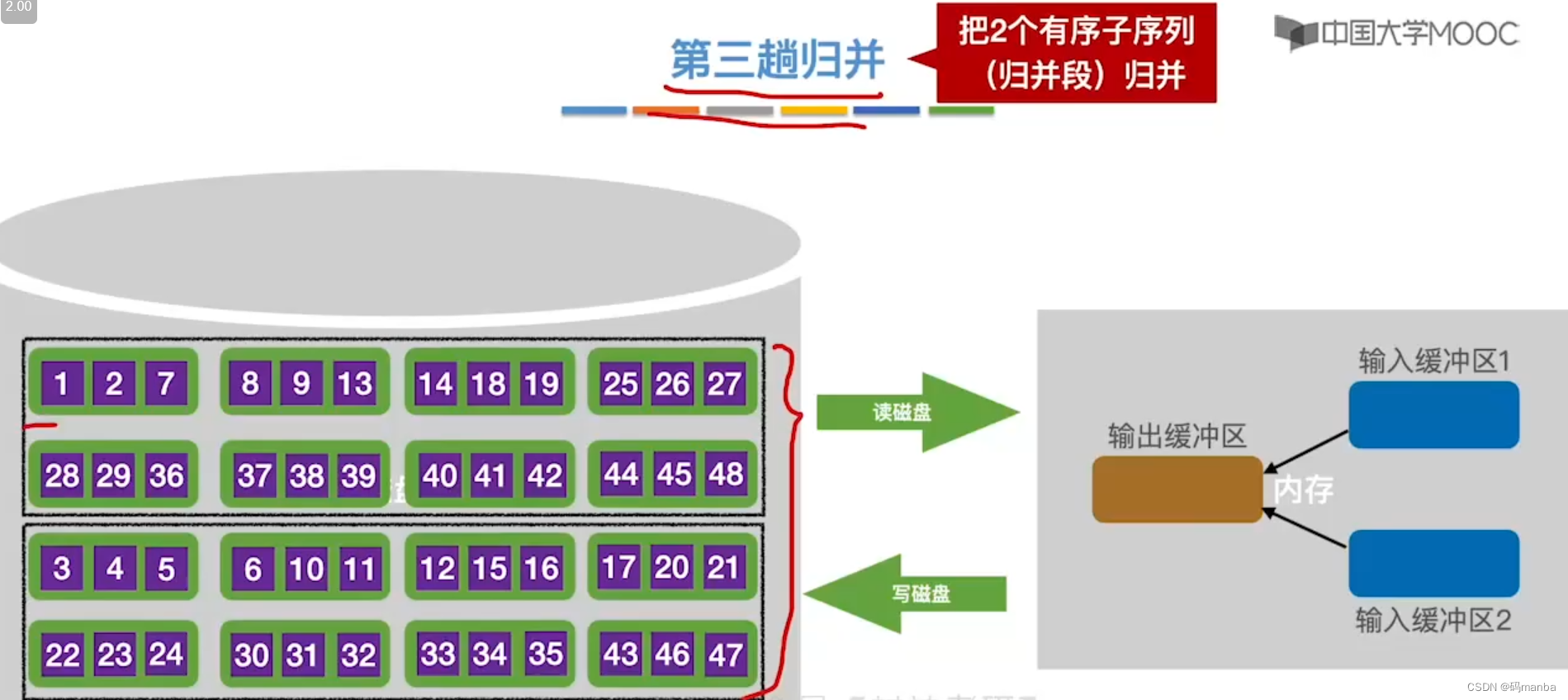
? 第三趟归并
- 归并方式同第二趟
- 在两个归并段,选最小的块读入到输入缓冲区。进行归并排序,放到输出缓冲区,满了就写回磁盘;
- 输入缓冲区空了就从对应归并段读入块;
- 直到所有数据排序结束;
7.3 外部排序的时间开销分析
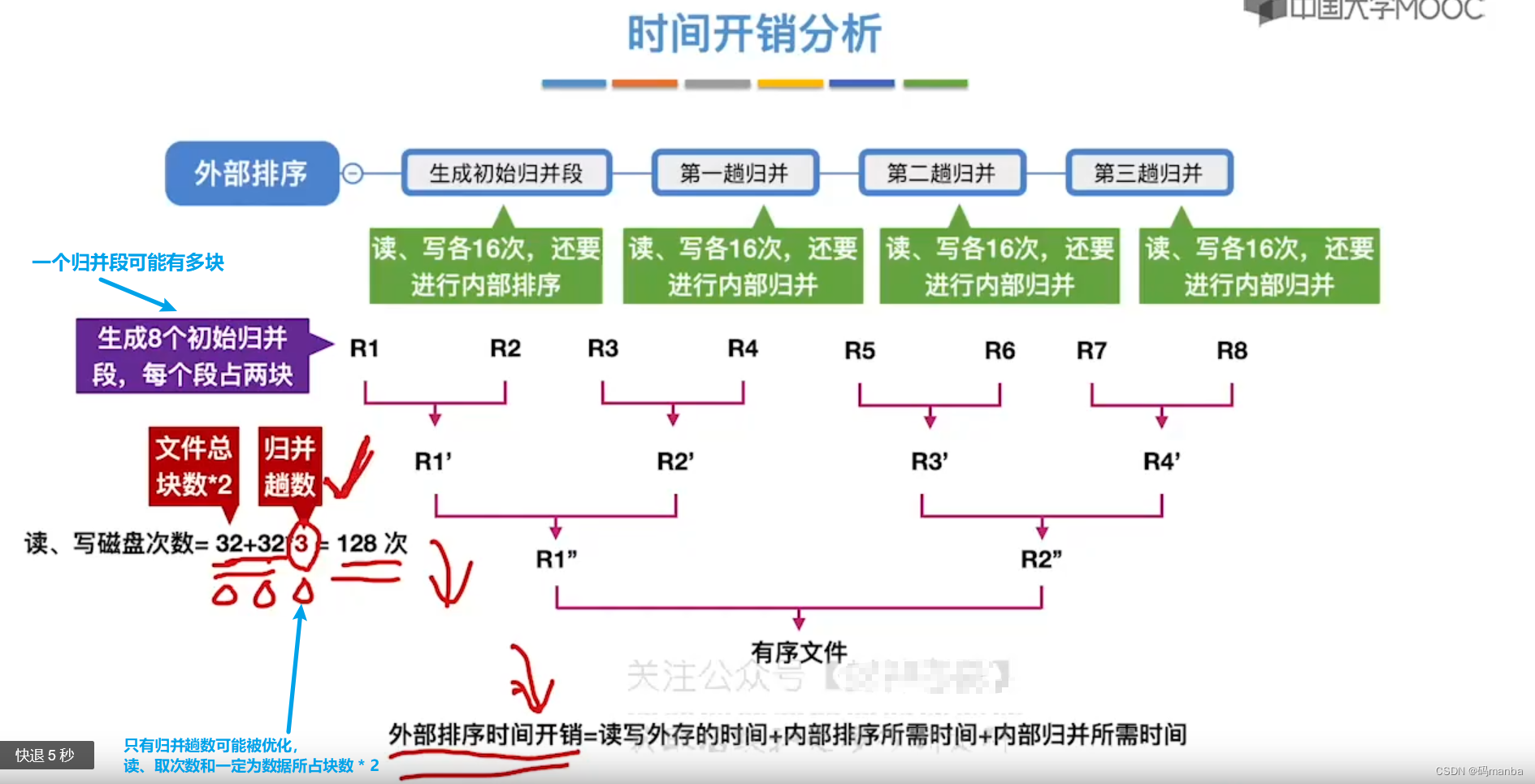
通过更多多路归并减少归并趟数从而起到优化作用
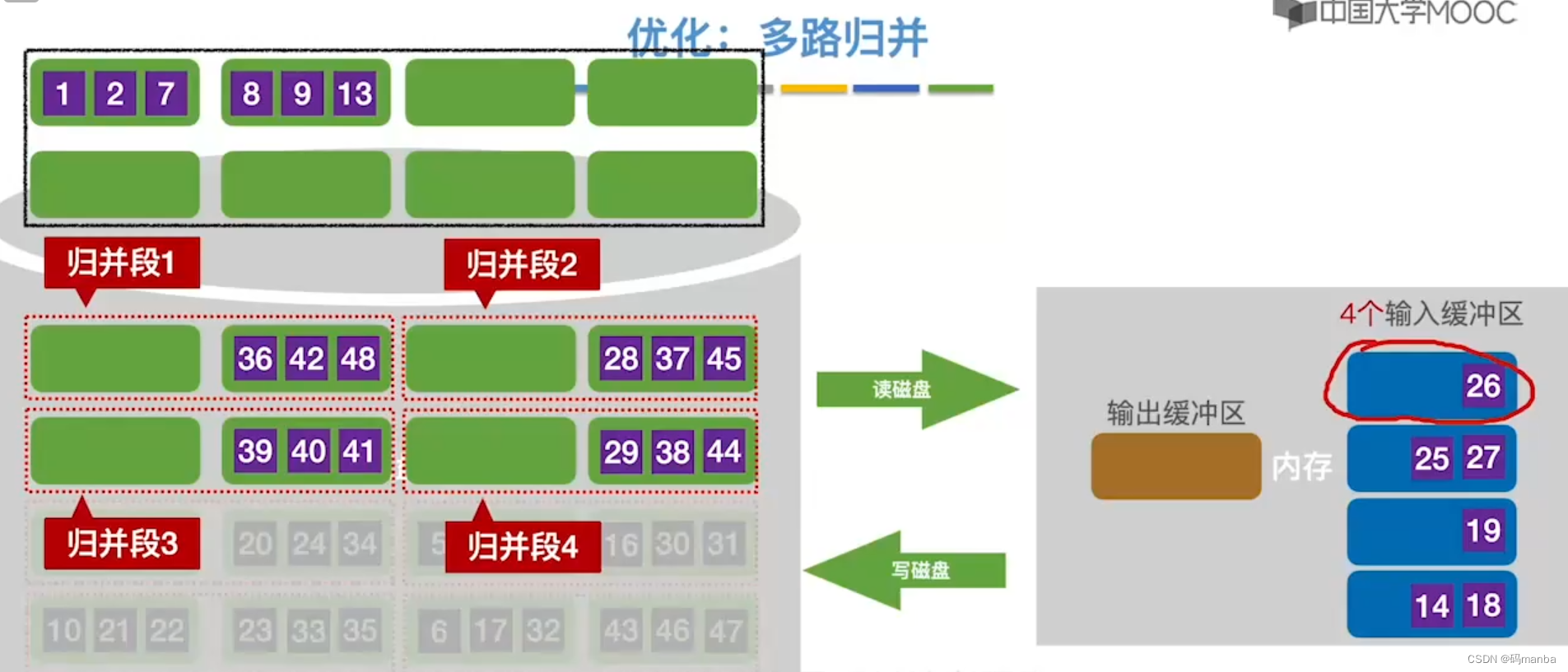
- k 越大, r越小;
- k表示 多路归并,也就是对应的k个输入缓冲区;
- r表示初始归并段, 也就是 把外存的块分成多少个归并段,归并段越少,其内部的块越多;
- 注意k变大带来的负面作用;
- 因为k是输入缓冲区,所以k越大,占用内存开销越大;
- k也代表的k路归并,而k路归并要进行(k-1)次比较,所以k越大,比较的次数越多;
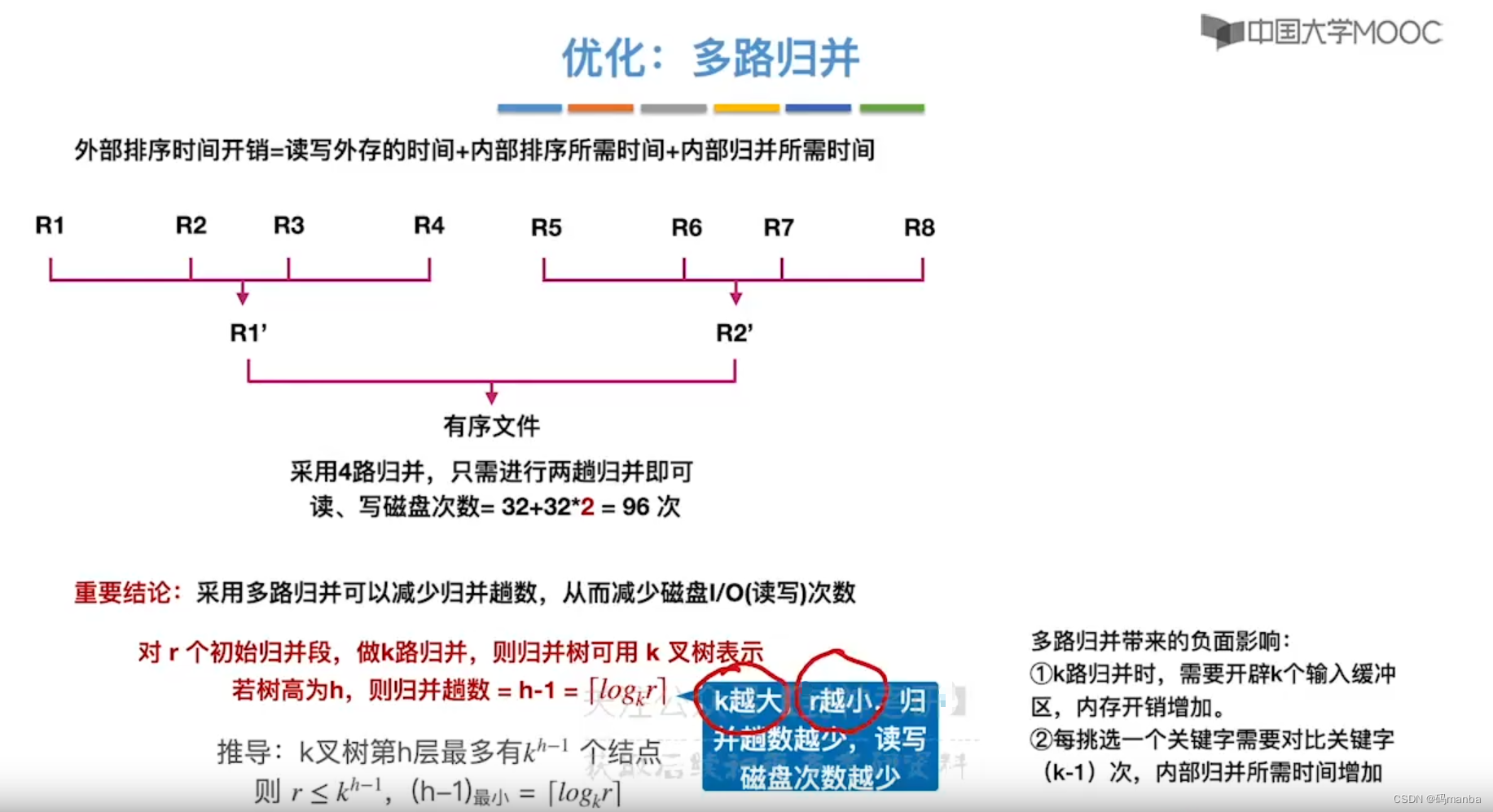
通过减少归并段(每个段的长度增加,也就是每个段的块数增加)
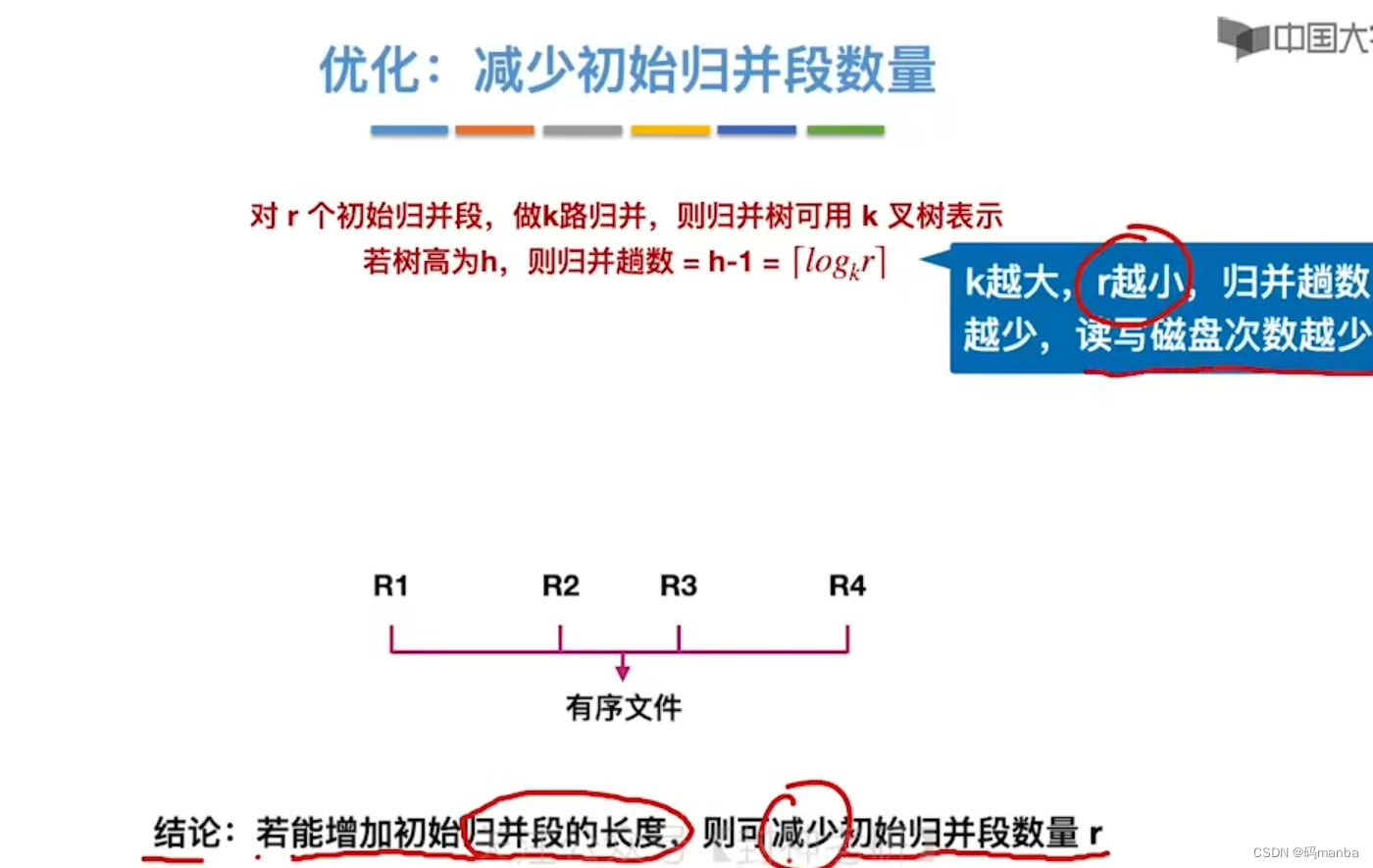
7.4 外部排序的知识总结
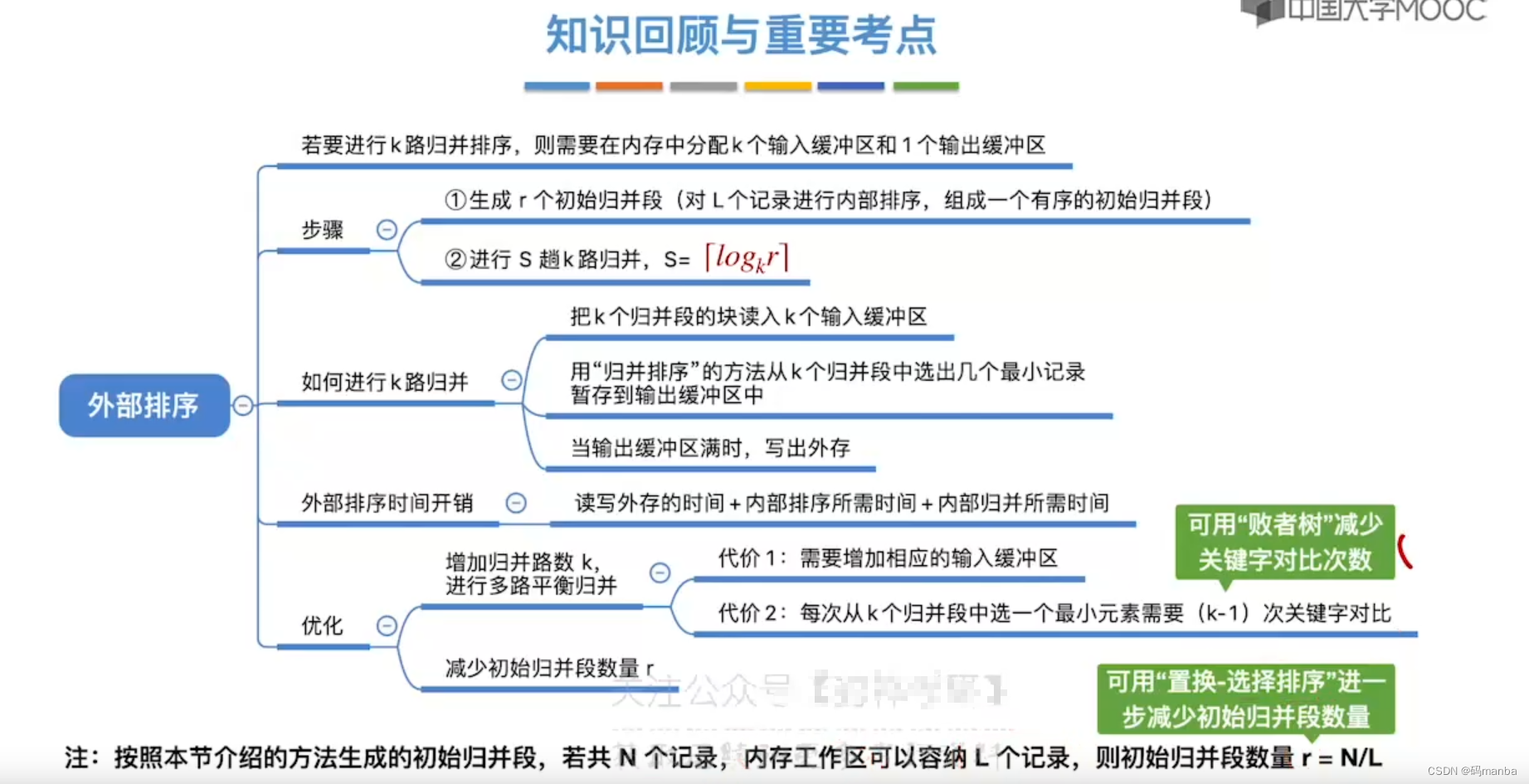
? 多路平衡归并概念纠正
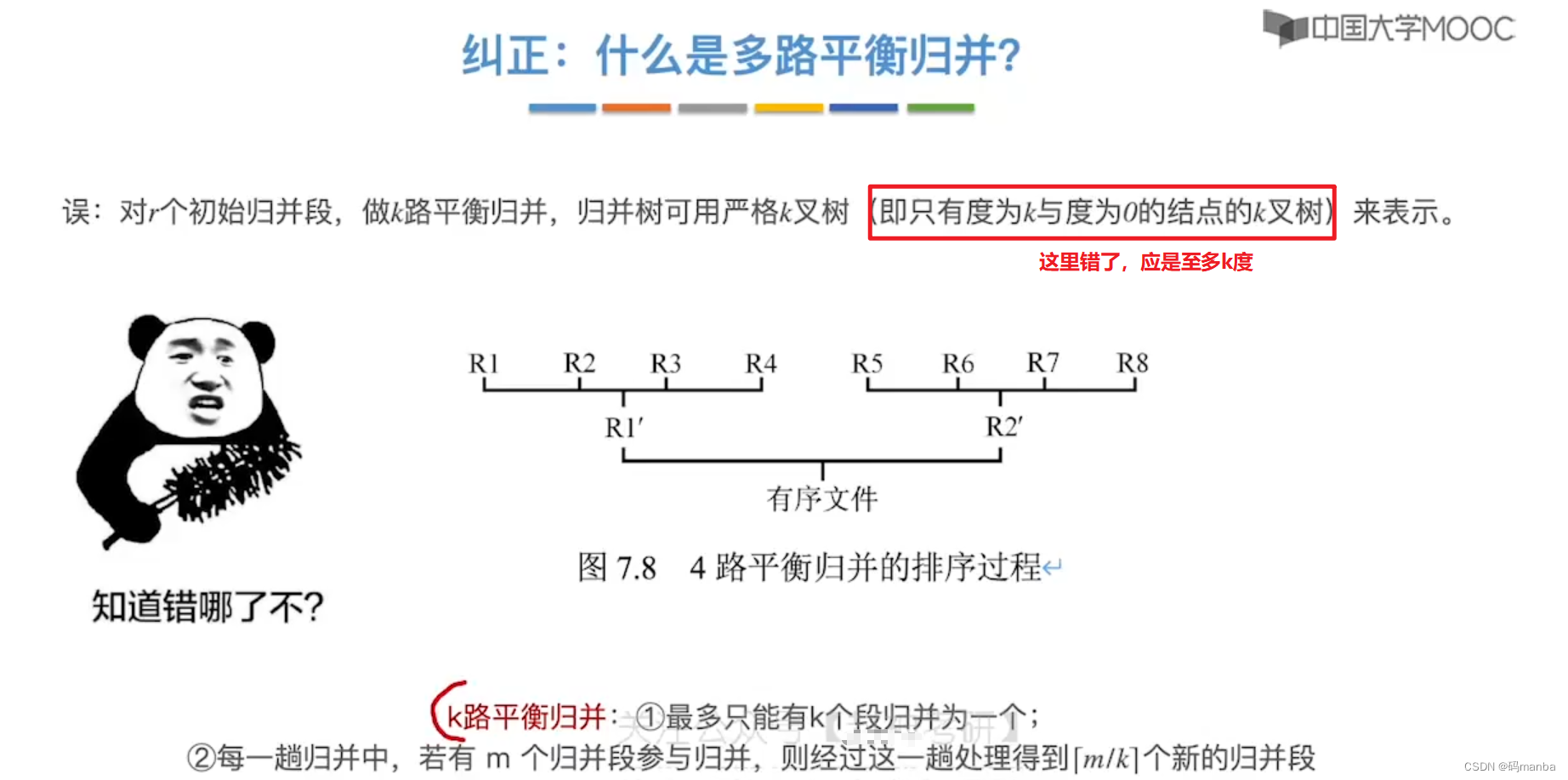
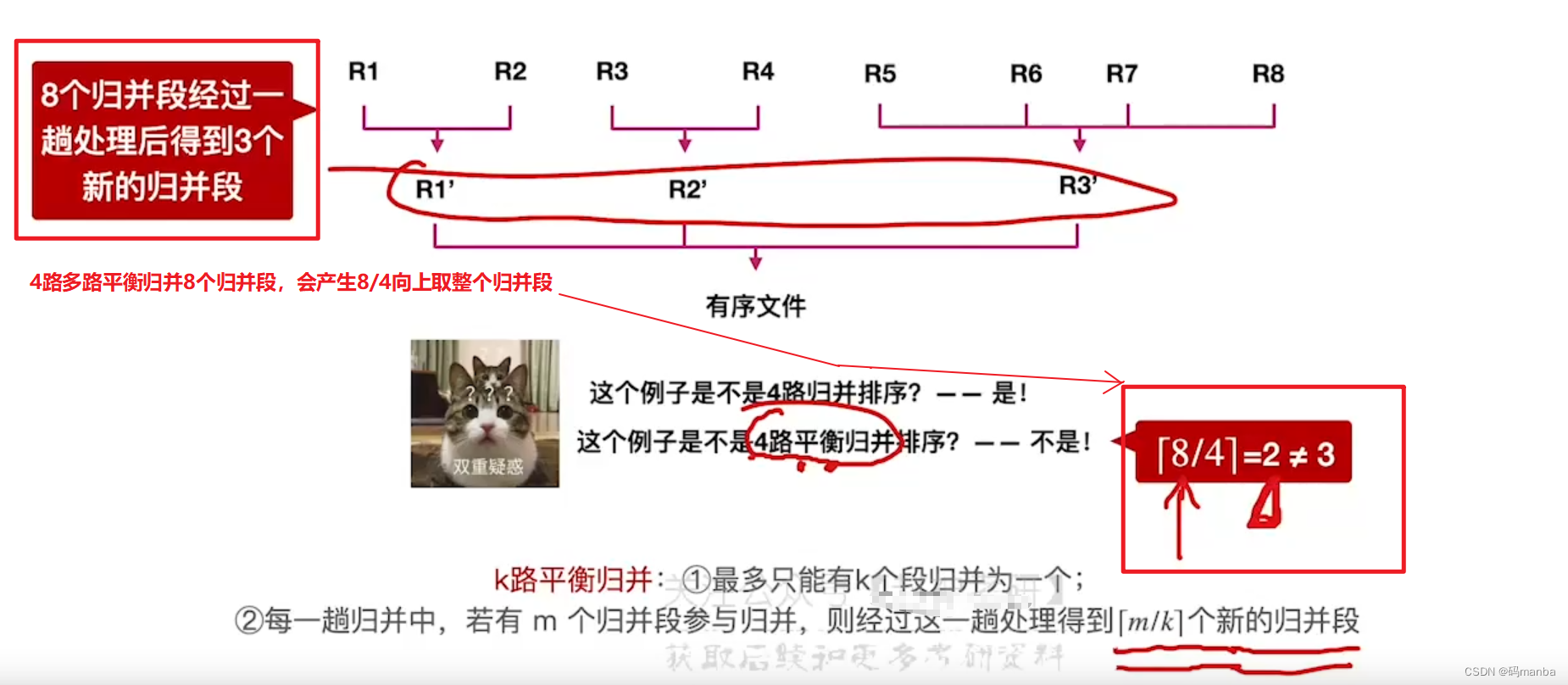
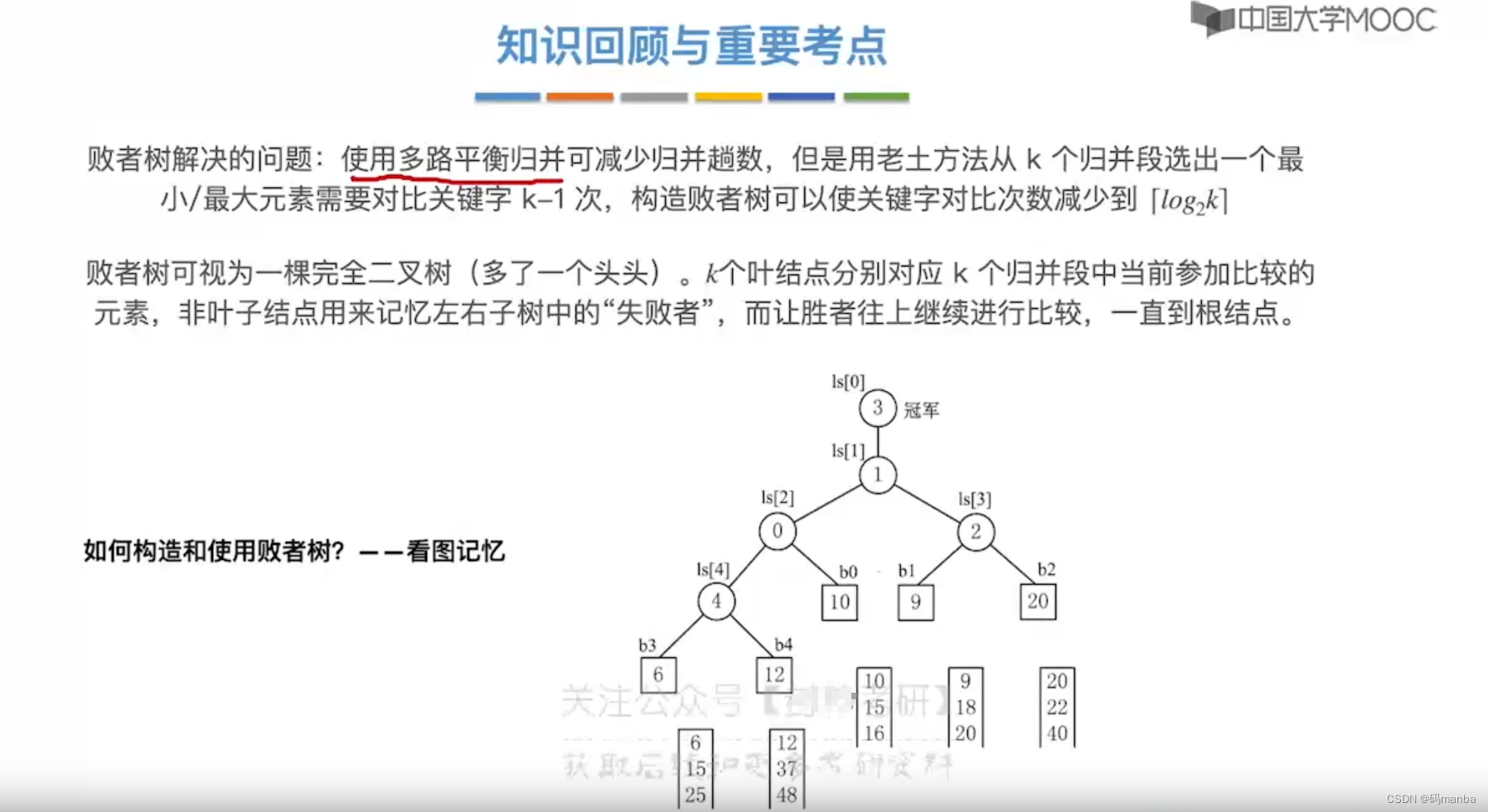
7.5 败者树(减少关键字对比次数。多路归并k增加时,关键字对比次数会增加)
多路平衡归并带来的问题(比较次数过多)
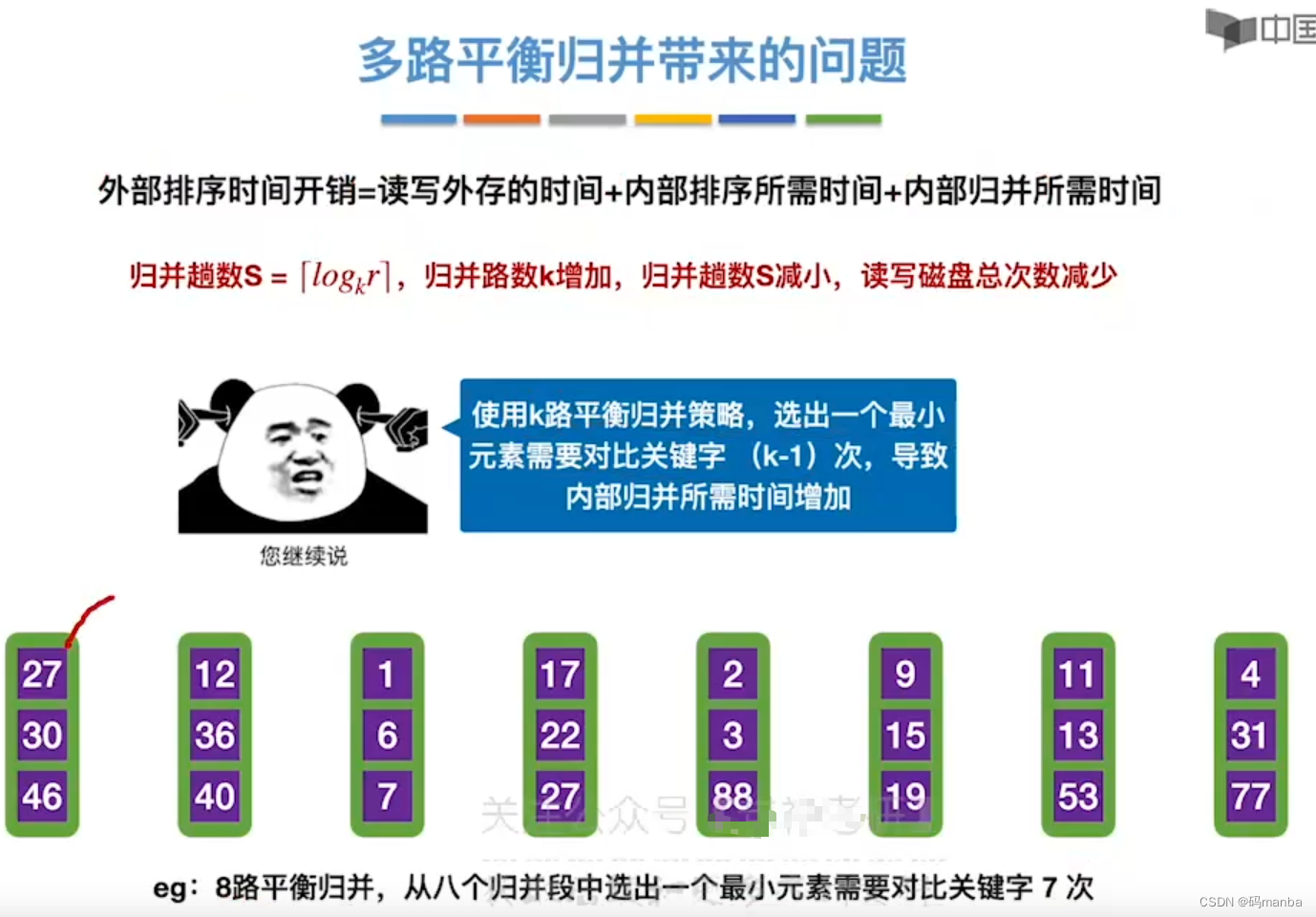
什么是败者树
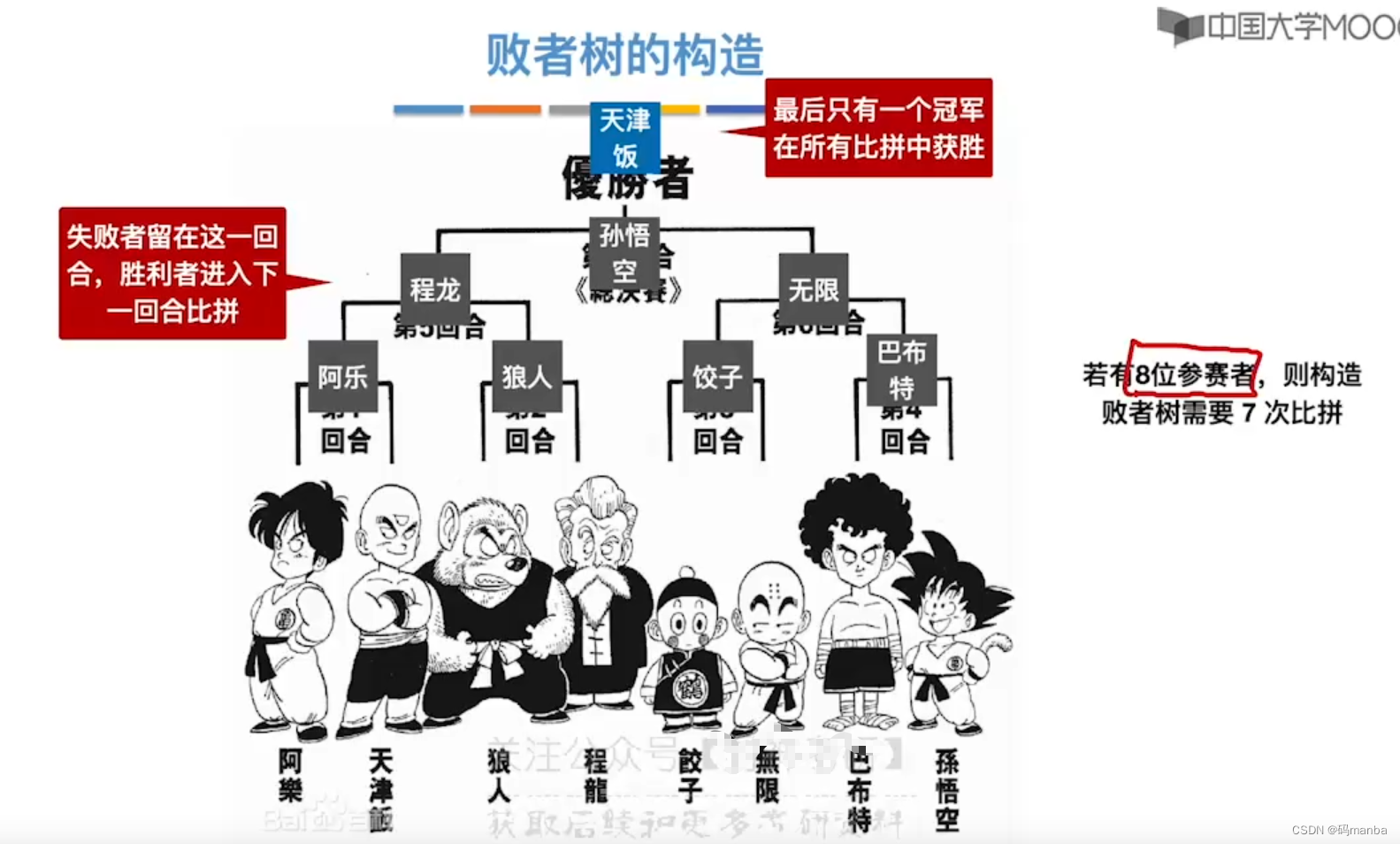
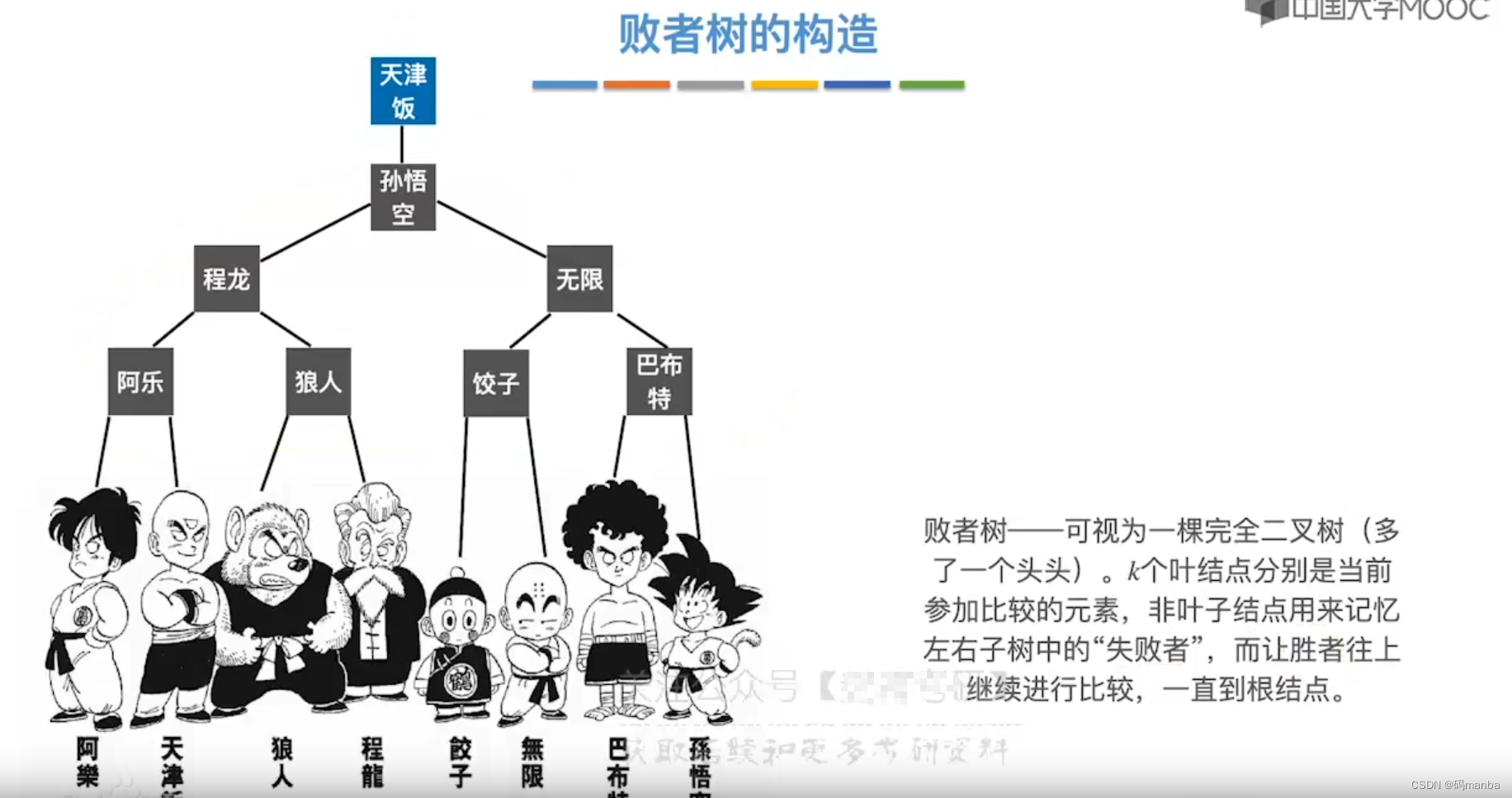
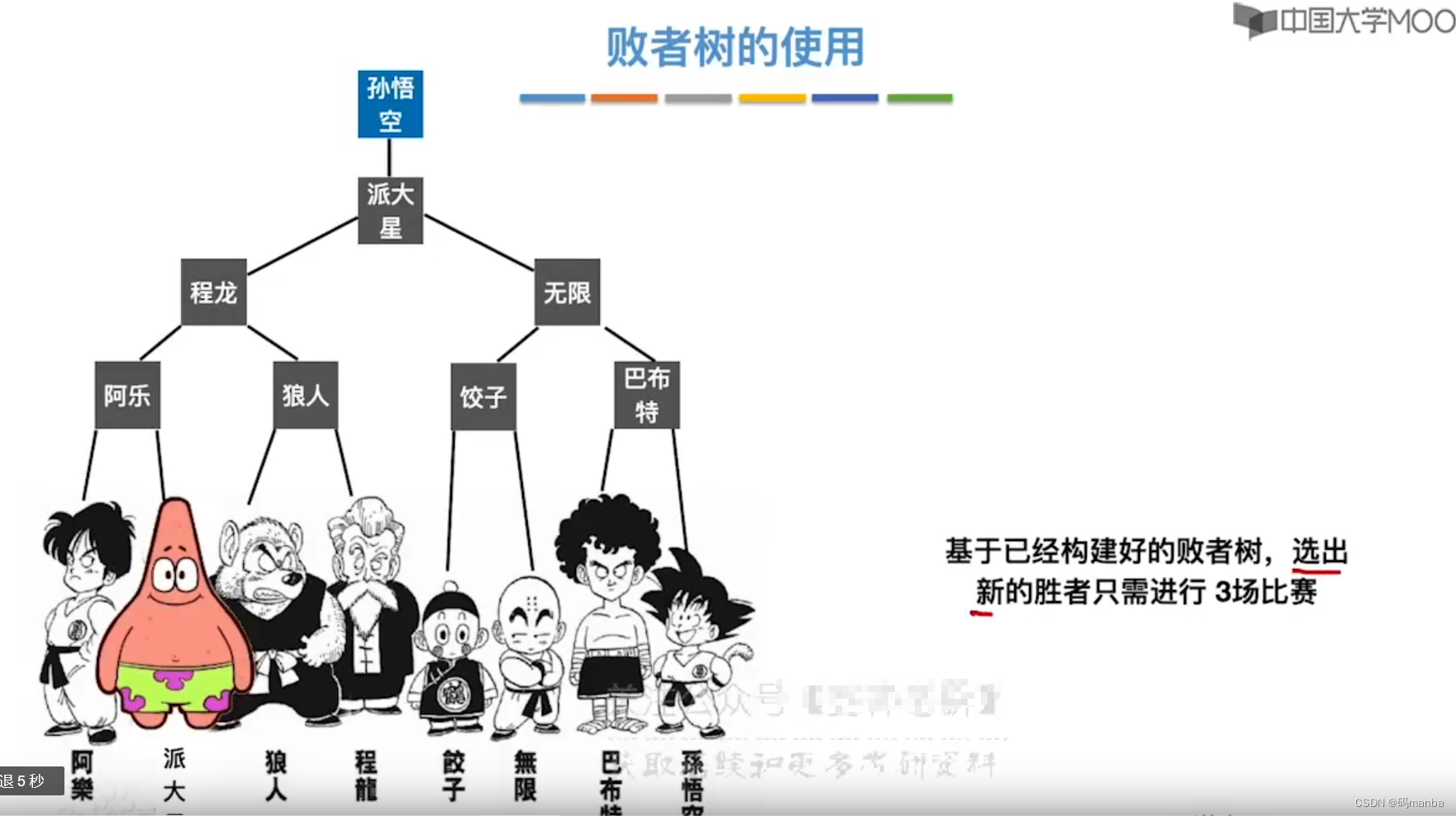
败者树在多路平衡归并中的应用
- 第一轮从每个段中选出一个元素进行对比,共对比n-1次;
- 根节点会记录胜利者所在段编号;
- 分支结点会记录在本轮中失败的段编号;
- 叶子节点保存了每个段派出的元素。
- 这样第一次选出一个最小的元素
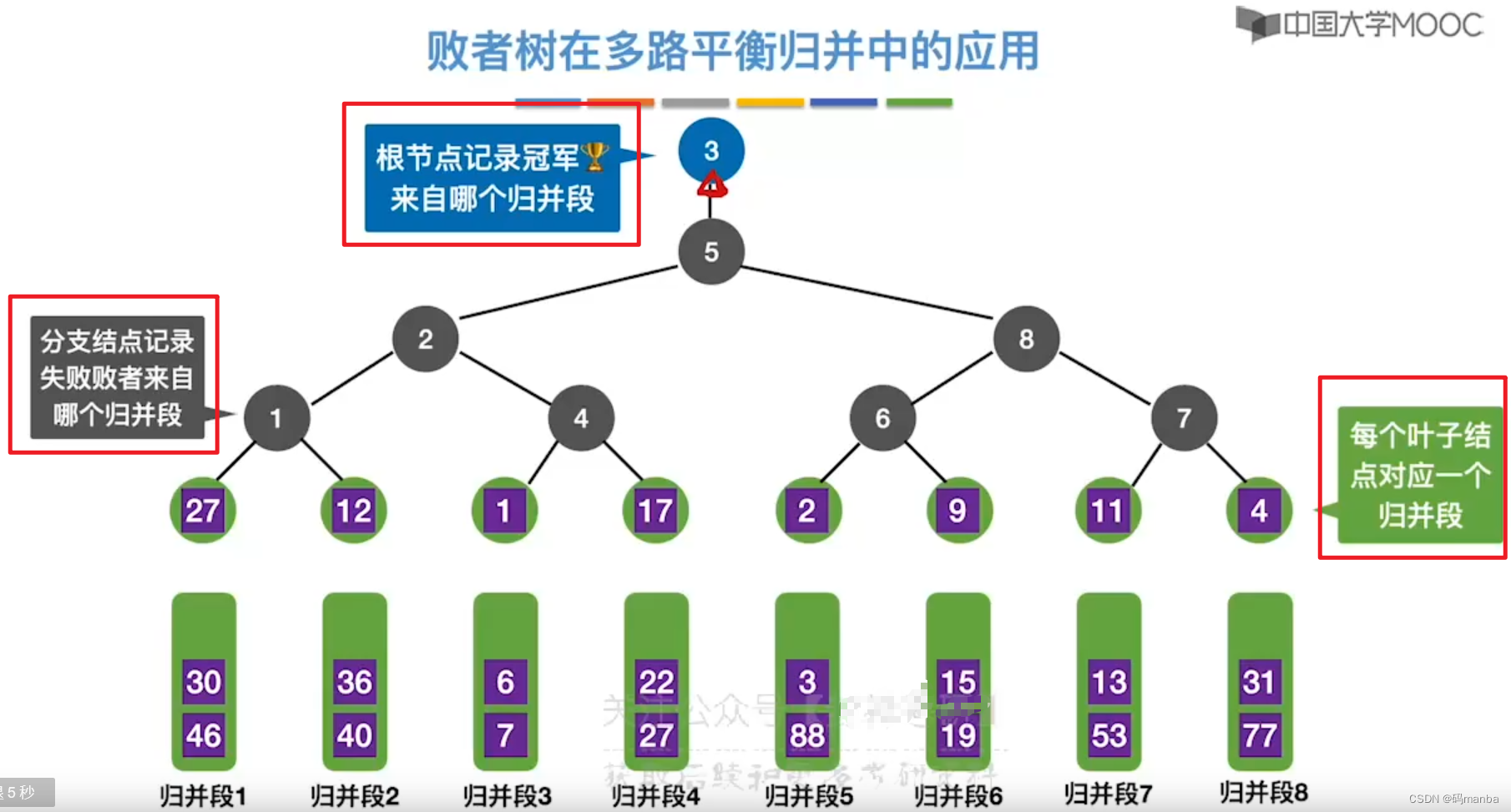
- 所在段在补充上一个元素,进行向上对比, 但是此时对比的次数就大大减少了,只需要比对数的层数 [log2k] 向上取整
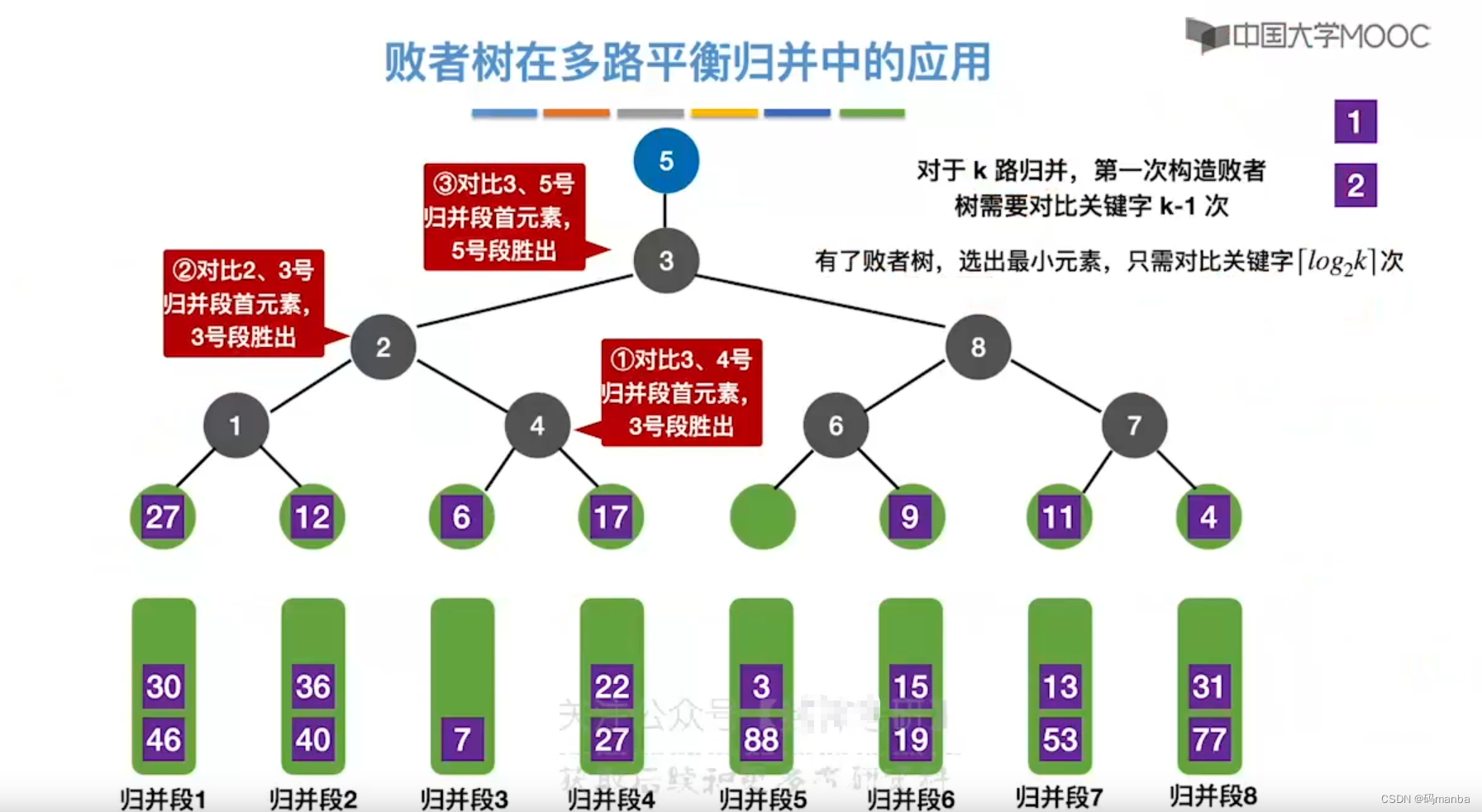
败者树知识回顾
7.6 置换-选择排序(减少初始归并段数量)
土办法构造初始归并段
- 首先看内存能容纳的记录个数: l;
- 然后看有多少个外存数据需要处理: n;
- 则初始归并段数量就是 n/l = r;
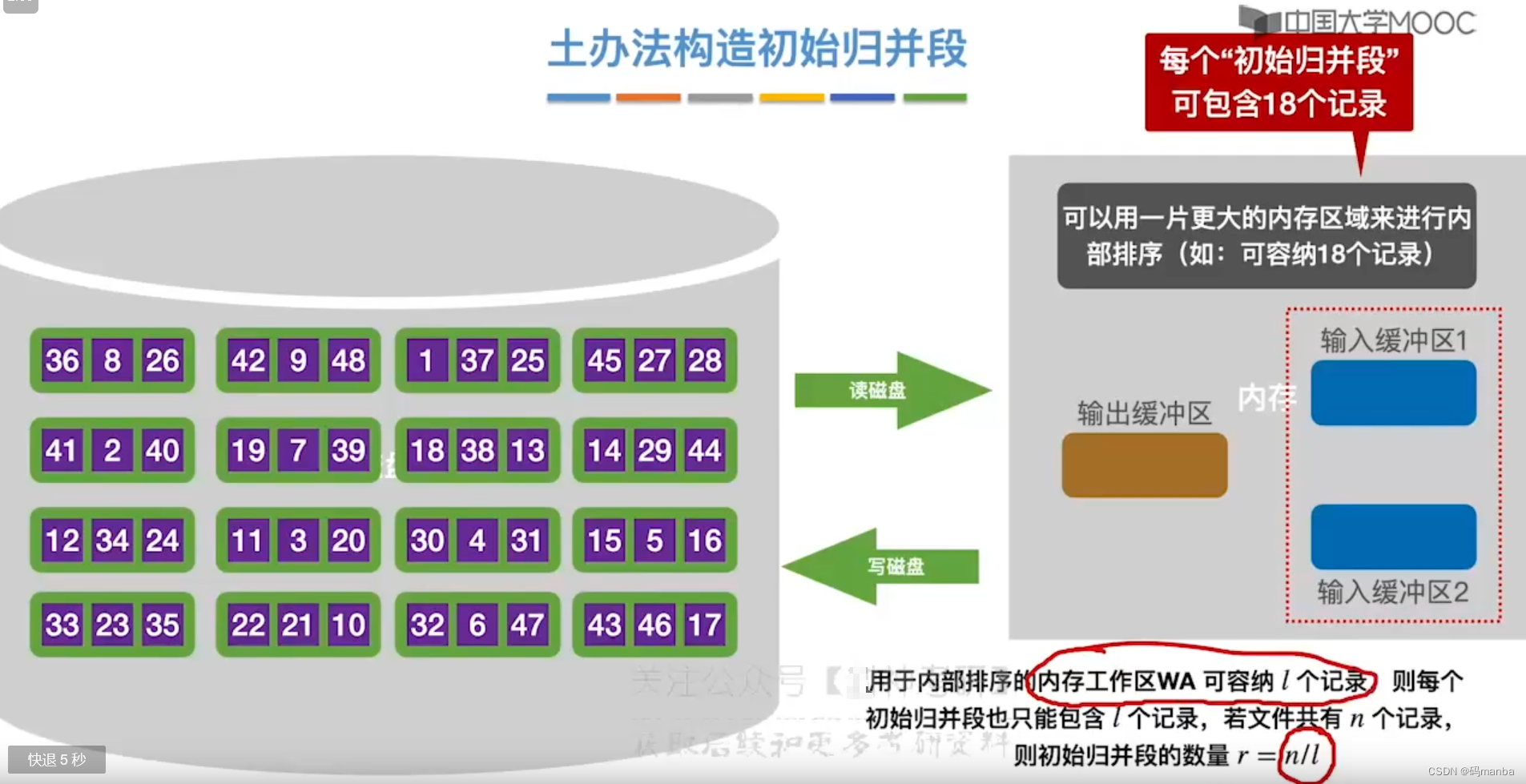
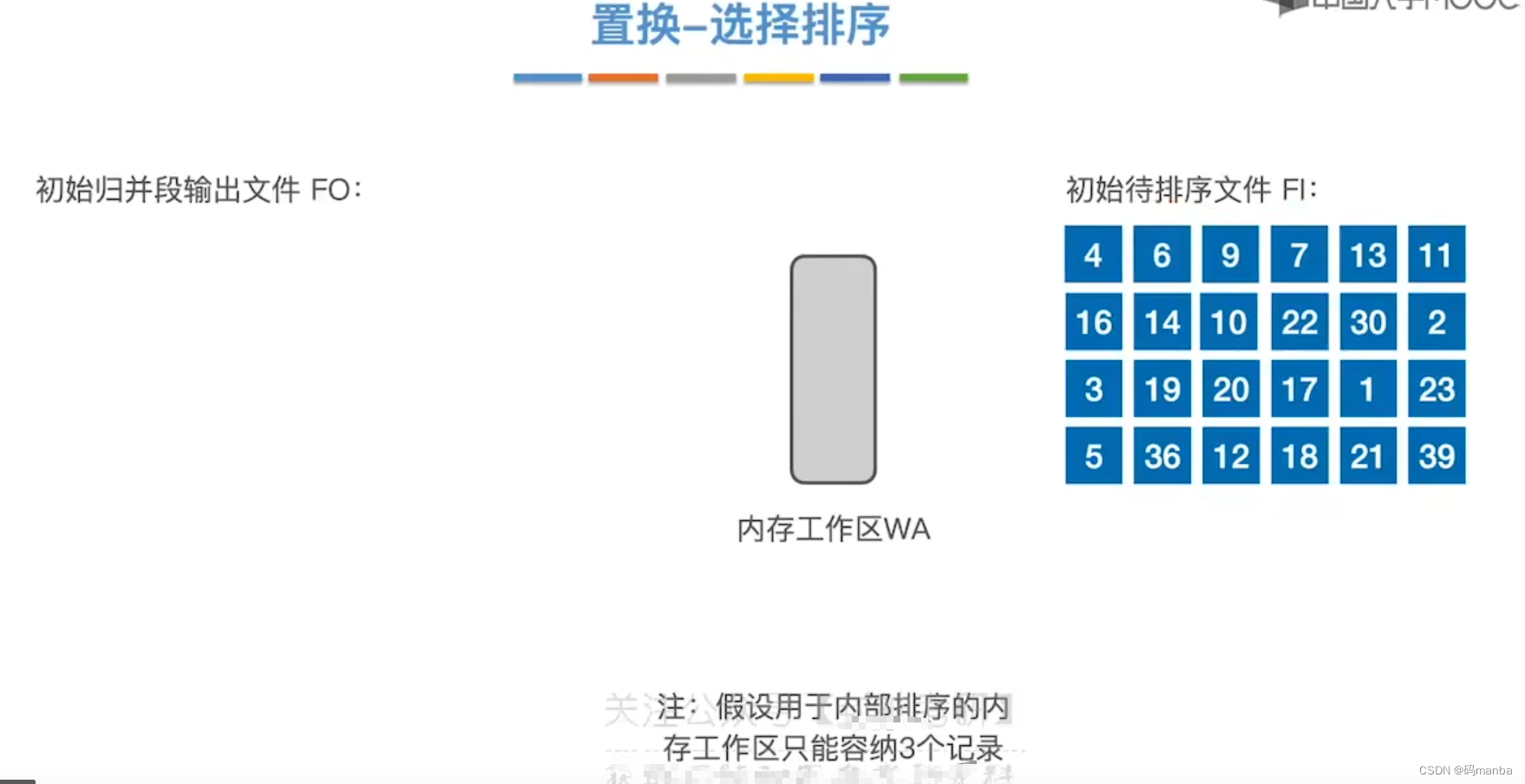
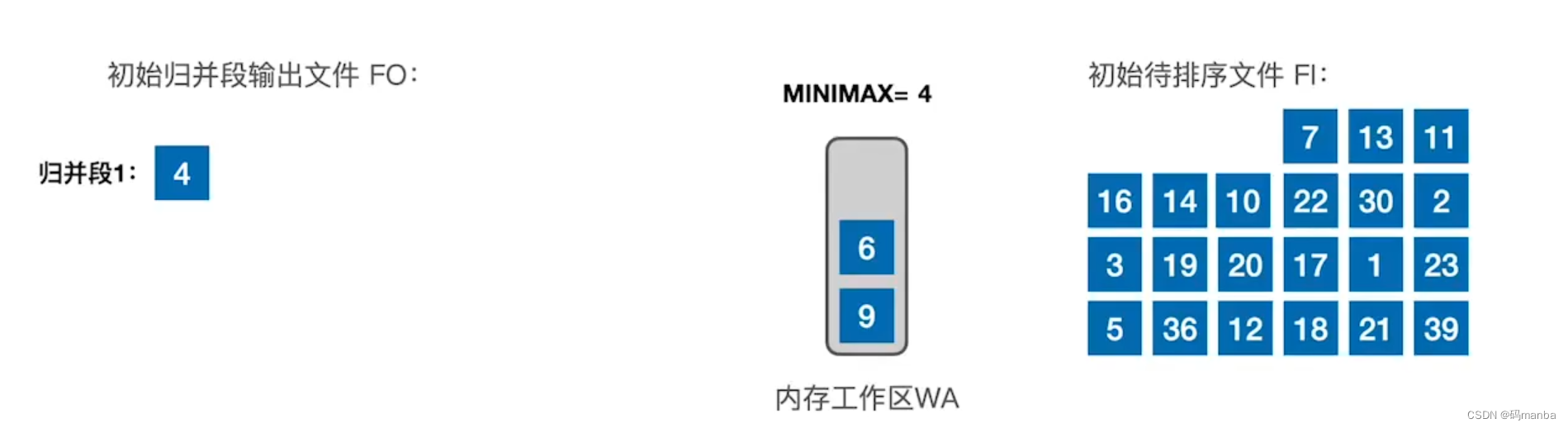
置换选择排序的实现步骤、思想
- 外存目前有24条记录, 内存工作区只能容纳3条,按照土方法, 初始归并块数量应为 8个;
? 确定第一个归并段
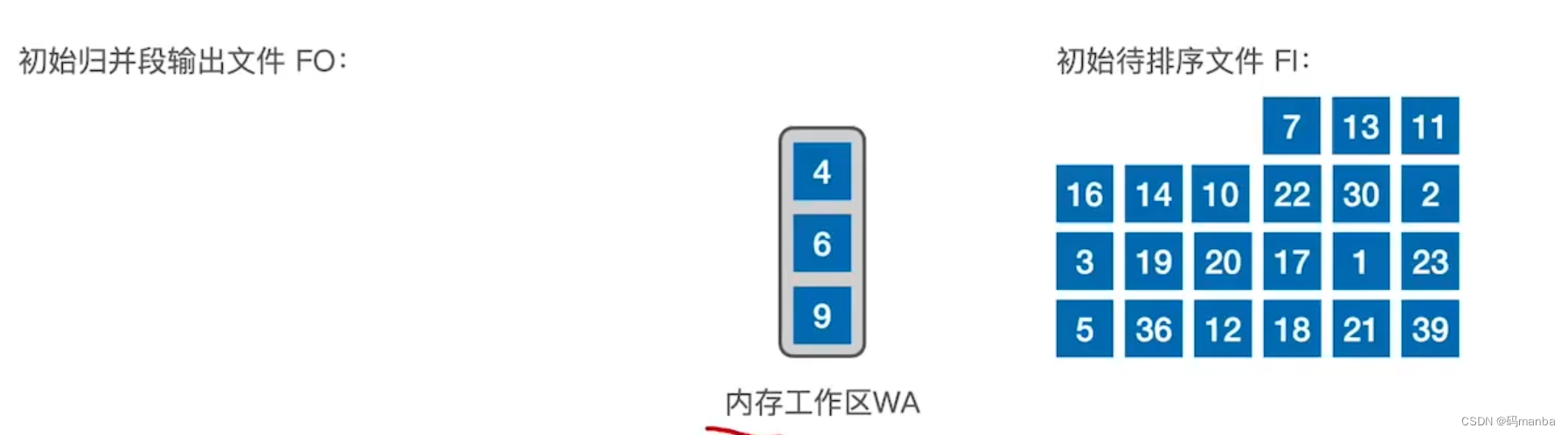
2.首先读入三个记录
3. ①将最小的元素放到输出缓冲区,②用minimax记录最小的元素值,③从外存中读入一个元素
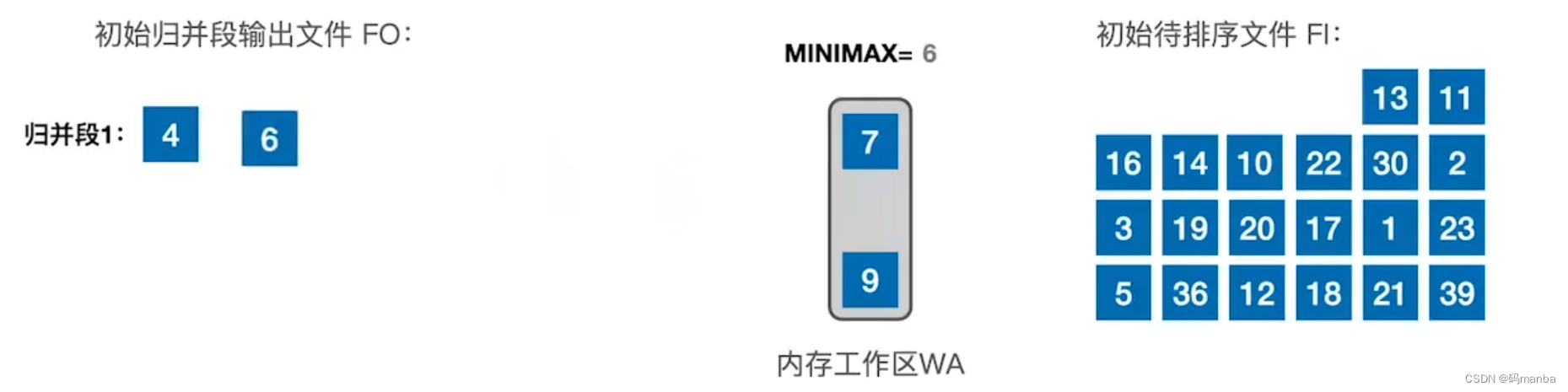
4. 读入元素后,①再找出一个最小值,②并且比较该值与minimax的大小, 如果大于minimax就放到输出缓冲区,并再从外存读入一个元素;
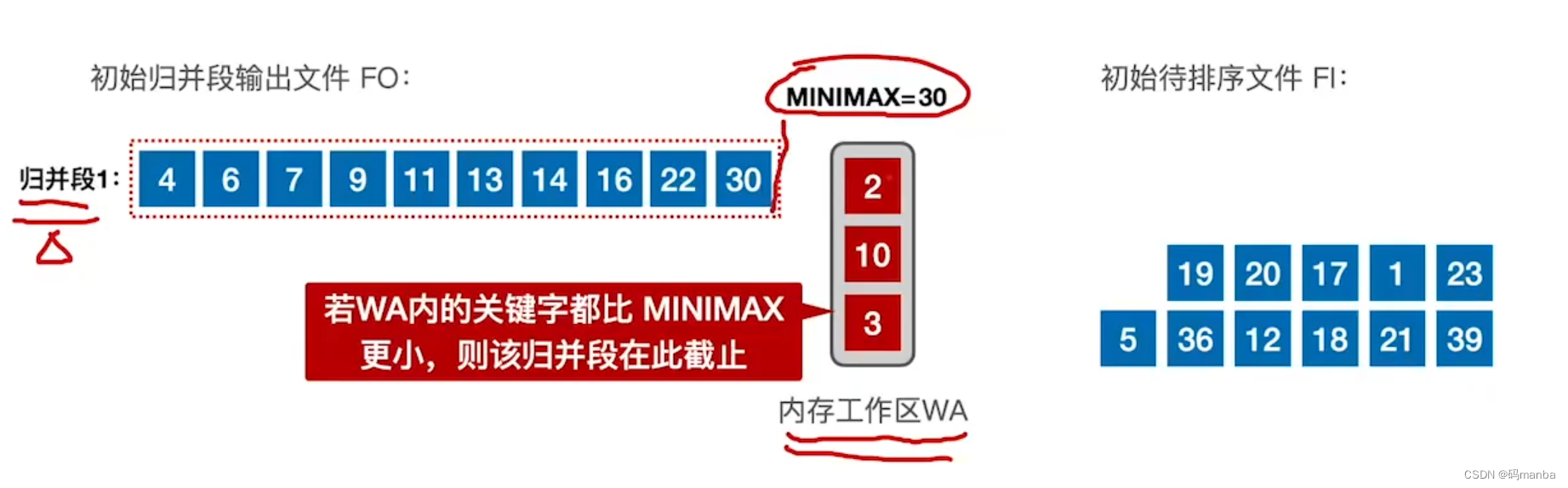
5. 一直如此,直到选出最小的值小于minimax。就将此数据标记, 然后除了该数据,再选个最小的看看是否小于minimax,如果小于就标记,大于就放到输出缓冲区, 输出缓冲区满了就写到外存;
6. 直到输入缓冲区所有元素都被标记;此时就确定了第一个归并段;
? 第二个归并段开始
- 在目前的输入内存缓冲区中选出一个最小的数据输出,并记录到minimax中,重复第一归并段选取规则;
? 接下来的归并段都是这样确定,直到所有元素被归并;
- 通过这种方式进行归并,归并段的长度可以超过缓冲区的长度;

置换选择排序知识回顾(代码文字描述)

7.7 最佳归并树(优化二路归并树为最佳归并树,也就是哈夫曼树)
归并树的神秘特性
- 读 磁盘的次数 = 写 磁盘的次数,等于归并树的WPL(带权路径长度,权值*到根结点长度的和)
- 而哈夫曼树的 带权路径长度是最小的,因此,我们让归并树成为哈弗曼树,就可以最小的读写磁盘;
- 下图绿色结点的数量为归并段中磁盘块的数量
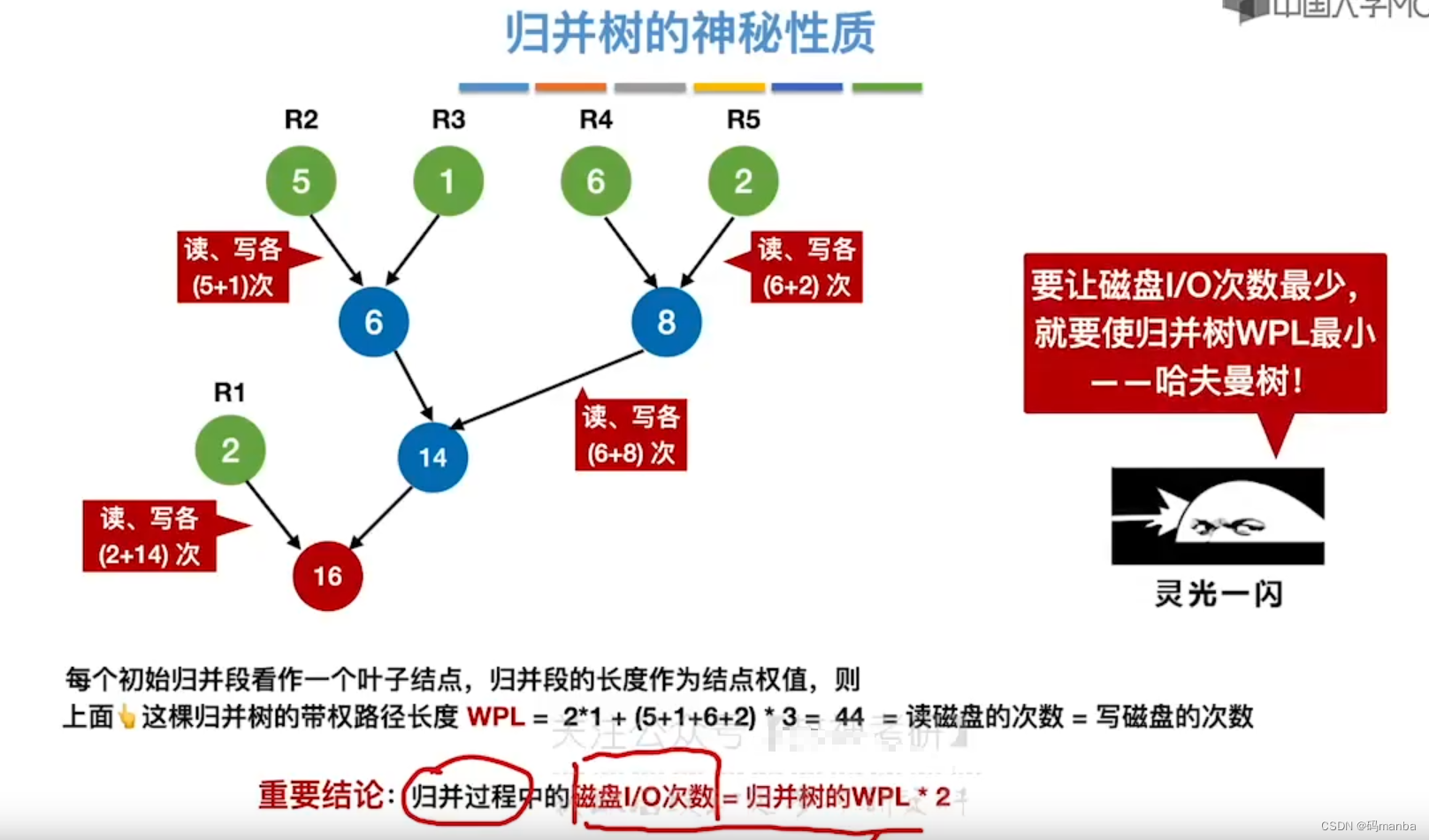
? 通过 构造2路归并的最佳归并树
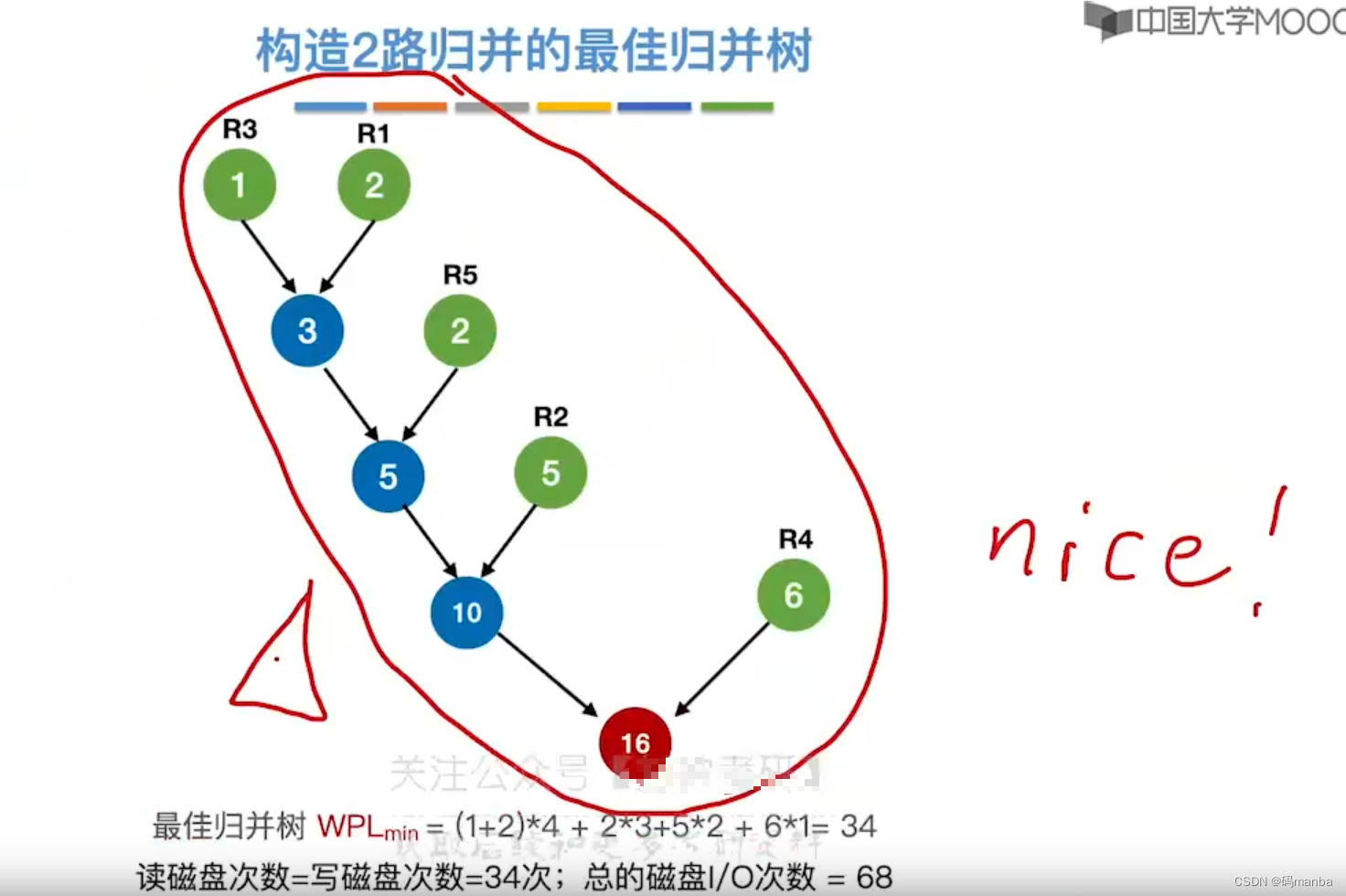
多路归并的最佳归并树
? 正常归并,读写次数很多
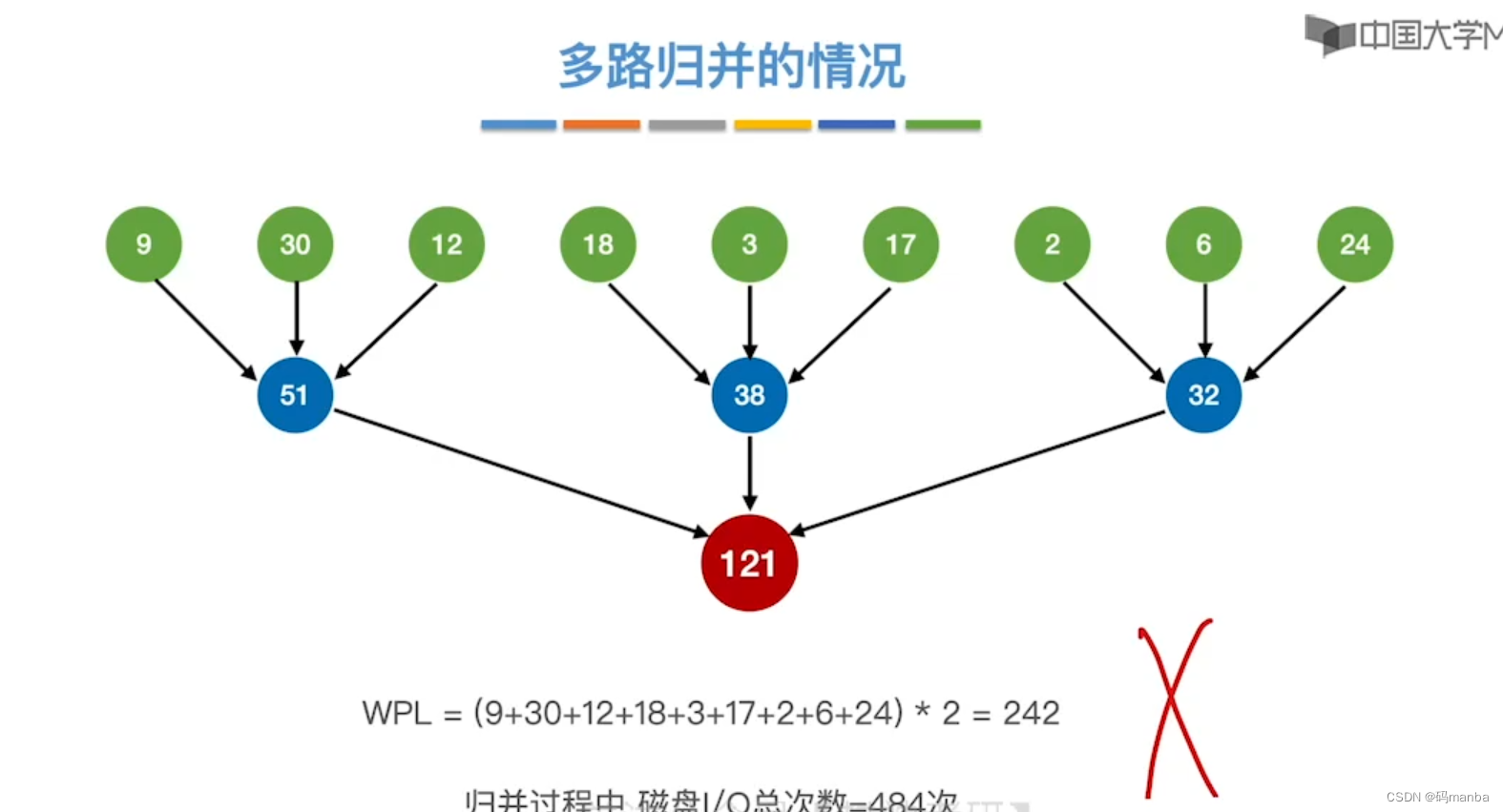
? 最佳归并
- 对于三路归并的最佳归并树
- 每次都选择最小的三个归并段
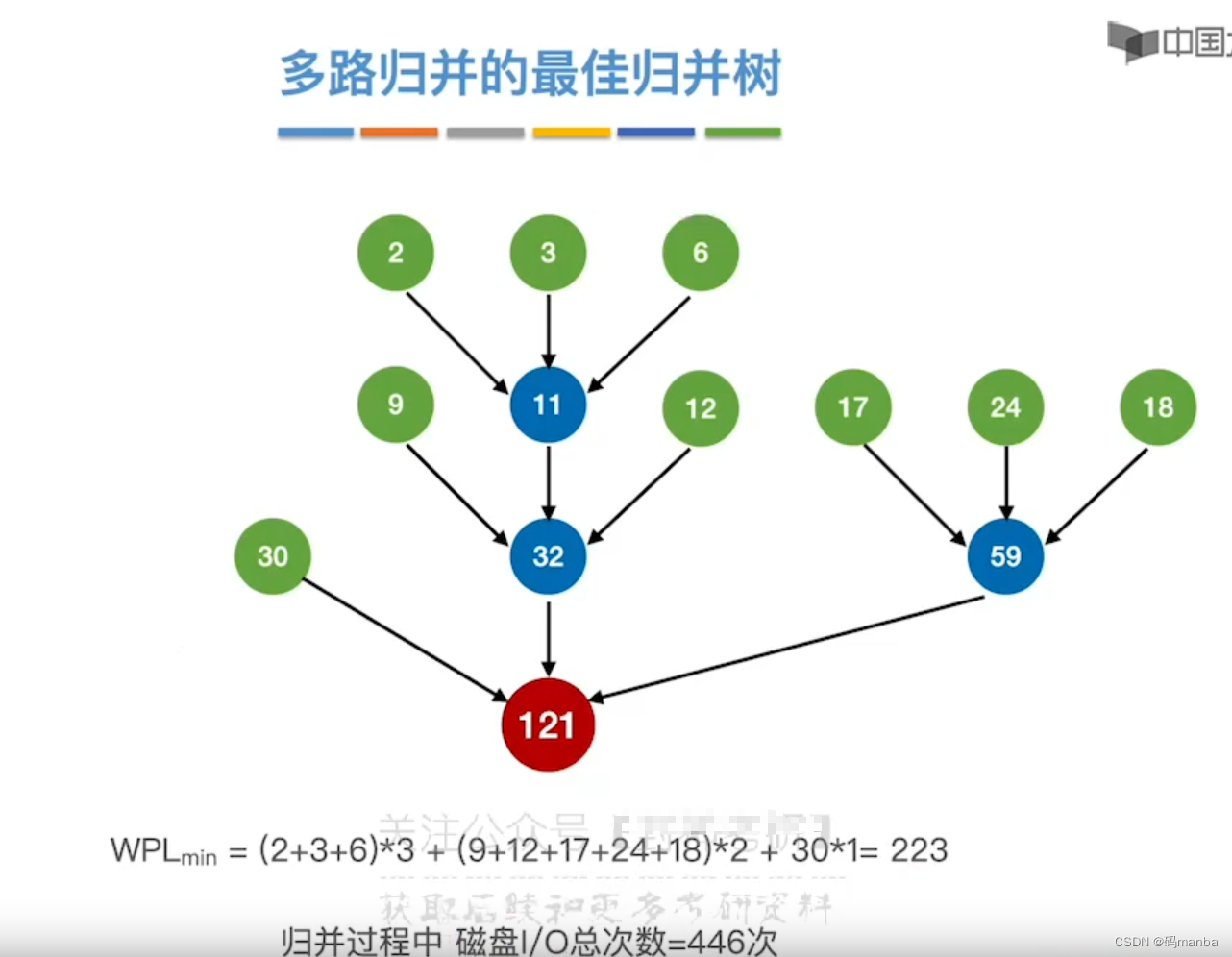
?? 注意如果对于k叉归并树,如果归并段不满足是k的整数倍应该增加虚段;
? 错误归并👇
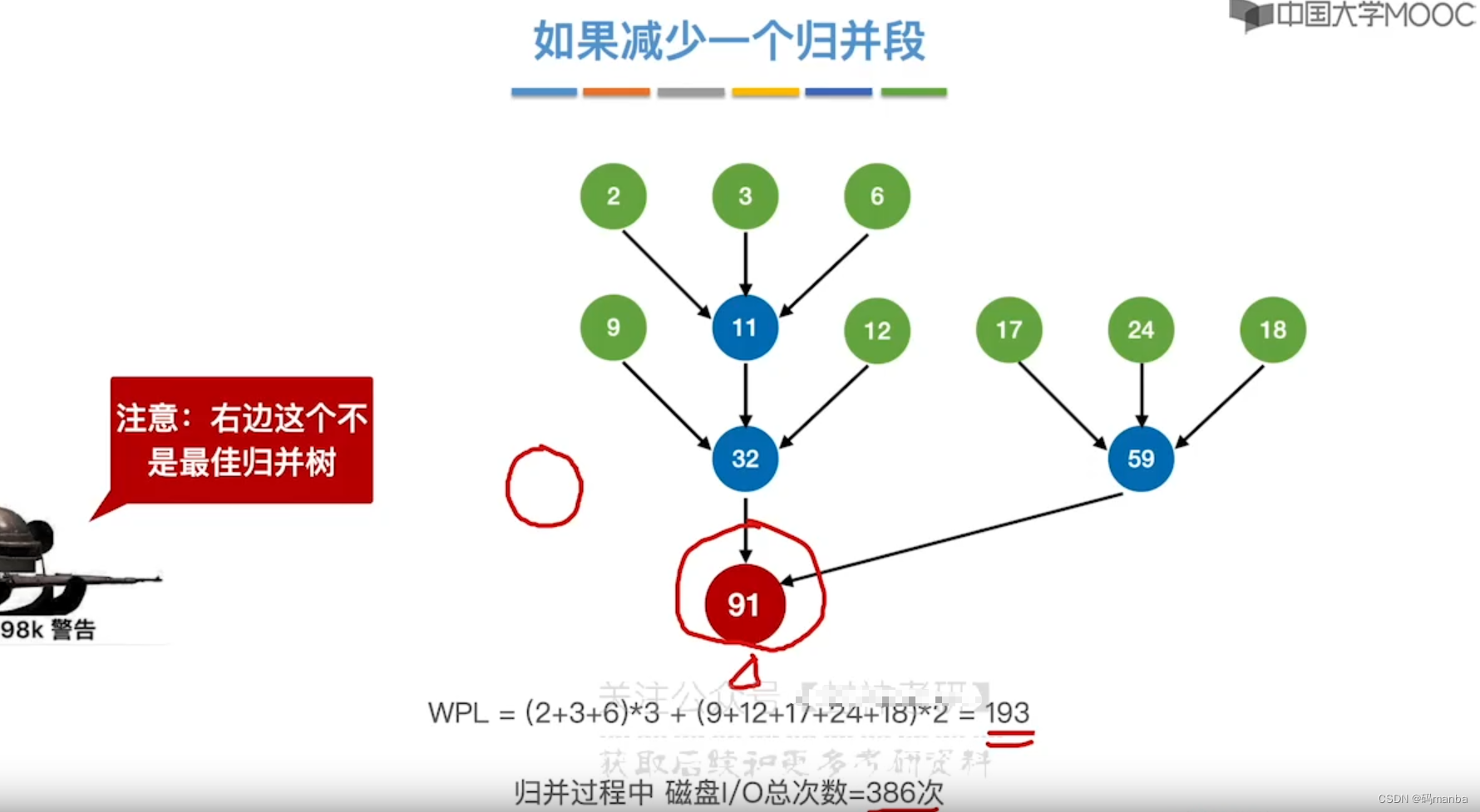
?正确归并👇
- 应该补0虚段来进行哈夫曼树的构造(也就是最佳归并树的归并)
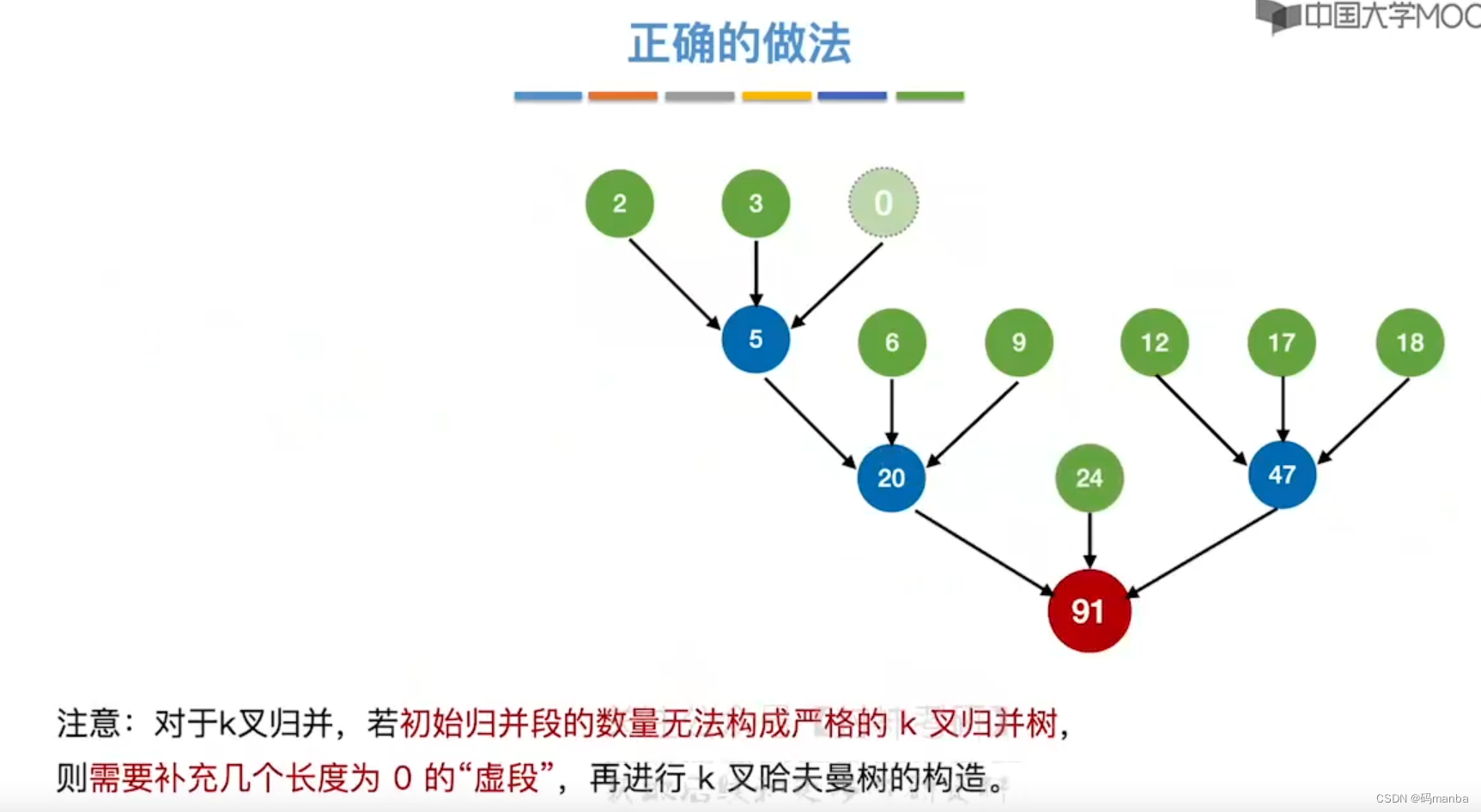
?那么应该步长多少个归并段?
- 初始归并段数为n, k叉树;
- 若 (n-1) % (k-1) == 0 ; 不用添加虚段;
- 若 (n-1) % (k-1) == u (u ≠ 0) ; 则应该 增加 k -1 - u 个虚段;

最佳归并树 知识点总结

八、 数据结构一轮结束