目录
🦄?链表的概念及结构
🦄?单链表OJ
?链表的概念及结构
概念：链表是一种物理存储结构上非连续、非顺序的存储结构，数据元素的逻辑顺序是通过链表中的指针链接次序实现的 。?
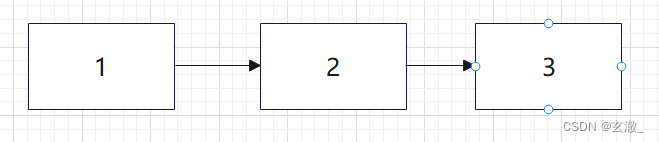
?大致的链表结构如下：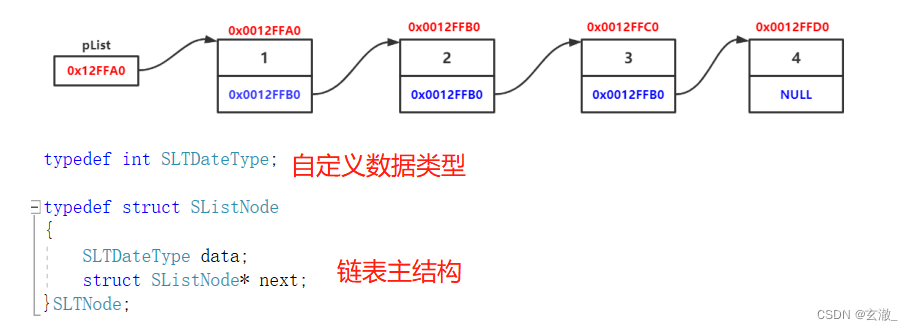
链表的打印函数?
接下来通过链表的打印函数来进一步理解链表的结构?
void SListPrint(SLTNode* phead)
{
SLTNode* cur = phead;
while(cur != NULL)
{
printf("%d->", cur->data);
cur = cur->next;
}
}?
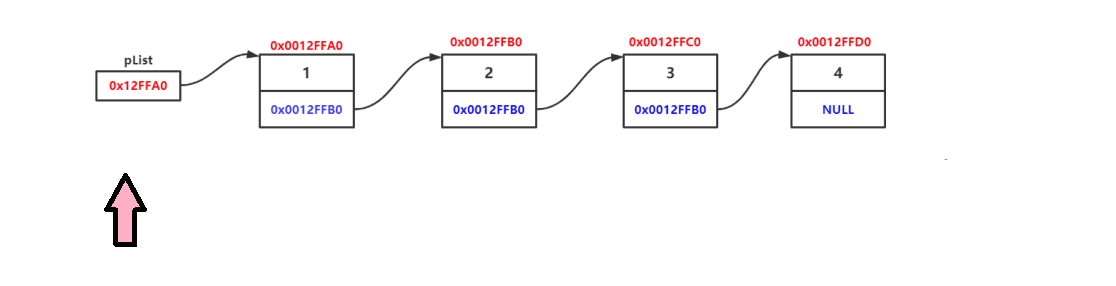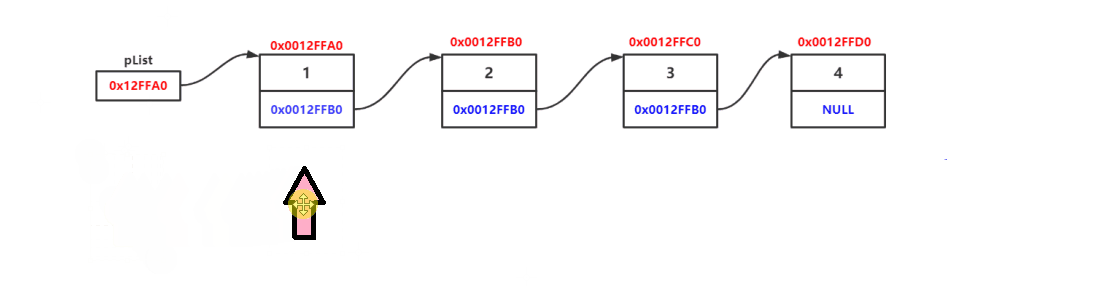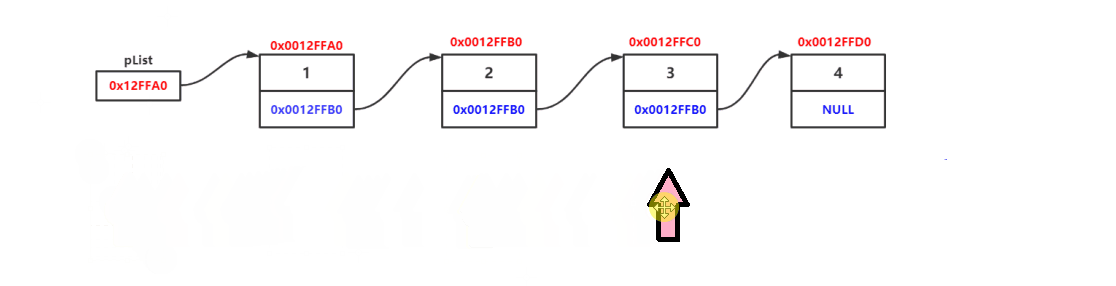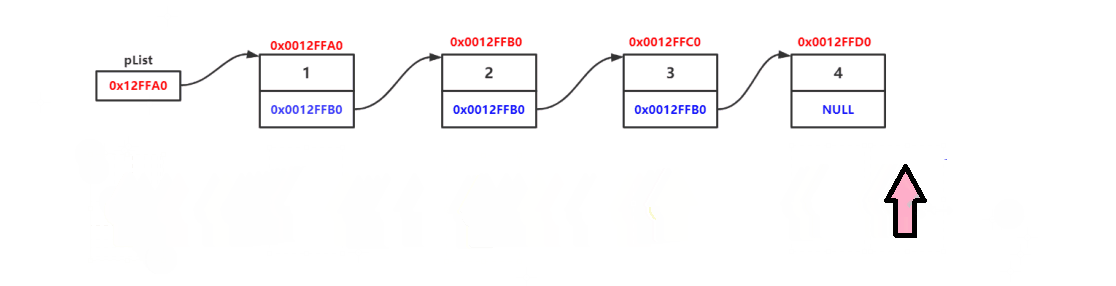
?由上述的打印函数可得，判断最后一个元素的判断依据是：next指针为NULL
链表的尾部插入元素函数
接下来我们实现在尾部插入一个元素
我们需要先找到尾结点，然后再接入一个新的结点
我们可以先写出来下面的代码：
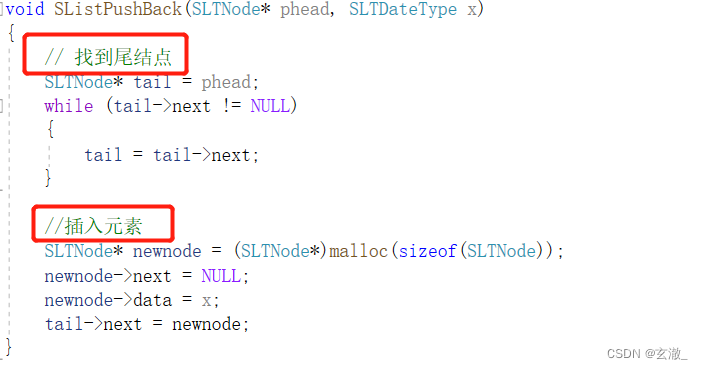
对于我们上面写出的代码，我们用一下程序来进行测试：
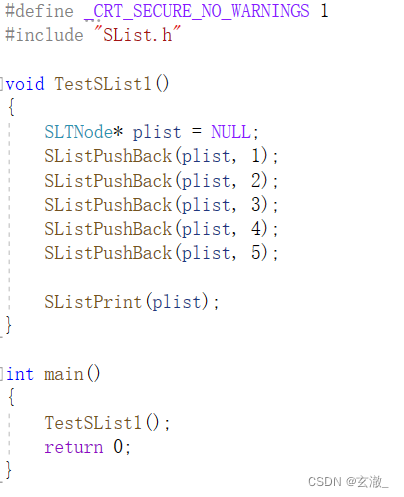
然后我们可以发现，程序崩溃了? ??
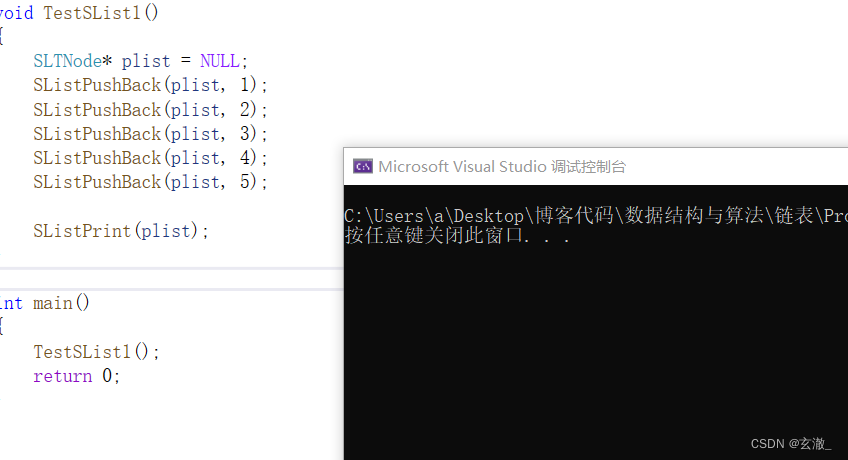?通过调试我们可以发现，我们最开始的链表头结点是NULL，我们通过这个头结点来进行查找尾结点的时候，会出现错误。
针对这个问题，我们需要进行一些优化（多一步判断条件）
同时还有一个问题，我们传入的是?int* phead,?在我们的函数中，它本质上还是一个形参，没有办法修改到原来的指针，所以，我们需要传入指针的指针，即?int** phead?才能真正修改原来的指针
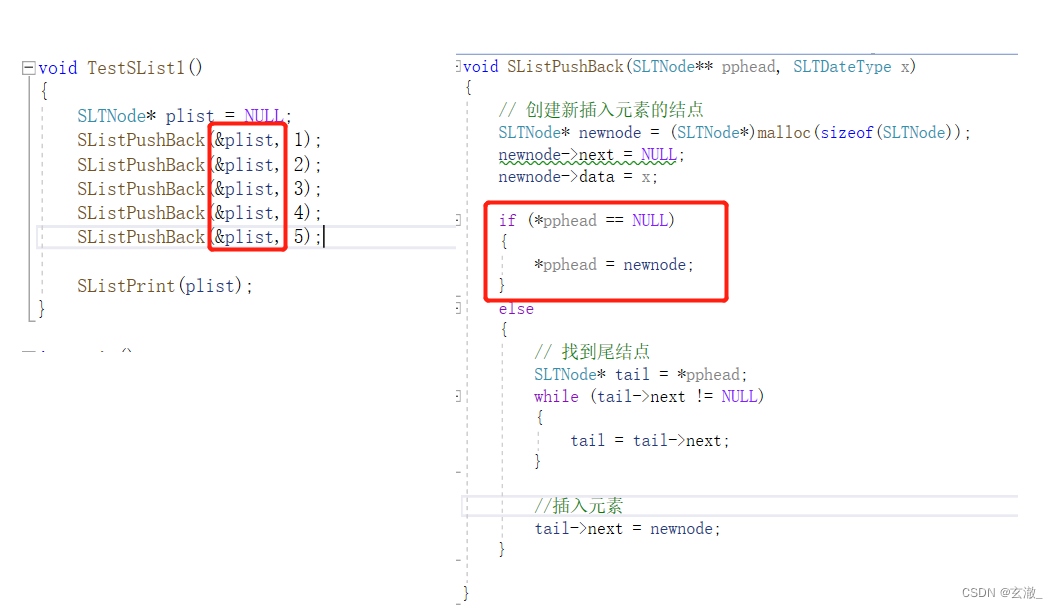
void SListPushBack(SLTNode** pphead, SLTDateType x) { // 创建新插入元素的结点 SLTNode* newnode = (SLTNode*)malloc(sizeof(SLTNode)); newnode->next = NULL; newnode->data = x; if (*pphead == NULL) { *pphead = newnode; } else { // 找到尾结点 SLTNode* tail = *pphead; while (tail->next != NULL) { tail = tail->next; } //插入元素 tail->next = newnode; } }
链表的头部插入元素函数
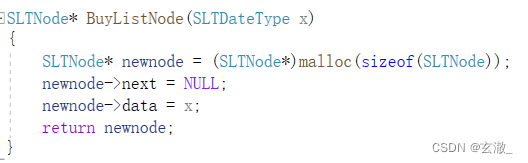
为了方便生成结点，我们写了一个?BuyList() 的函数
然后进一步实现头插函数，先将新结点指向头结点的下一个结点，再将新结点接到头结点后面
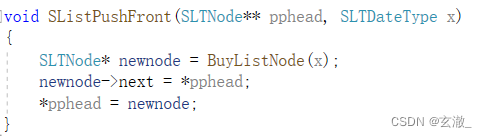
我们可以发现，在头插的情况下，就就算是空链表也不会出现问题，所以不需要多一步的判断操作?
删除操作（头删+尾删）
由于单链表无法找到前置元素，所以需要用类似双指针的方法来保留前一个元素的地址
但是上述代码还存在问题，当链表元素的个数只有一个或者是为空时，该代码会运行崩溃
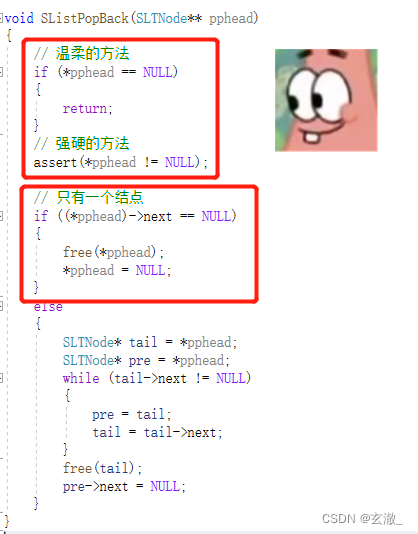
void SListPopBack(SLTNode** pphead) { // 温柔的方法 if (*pphead == NULL) { return; } // 强硬的方法 assert(*pphead != NULL); // 只有一个结点 if ((*pphead)->next == NULL) { free(*pphead); *pphead = NULL; } else { SLTNode* tail = *pphead; SLTNode* pre = *pphead; while (tail->next != NULL) { pre = tail; tail = tail->next; } free(tail); pre->next = NULL; } }
头删操作?
?查找函数的实现
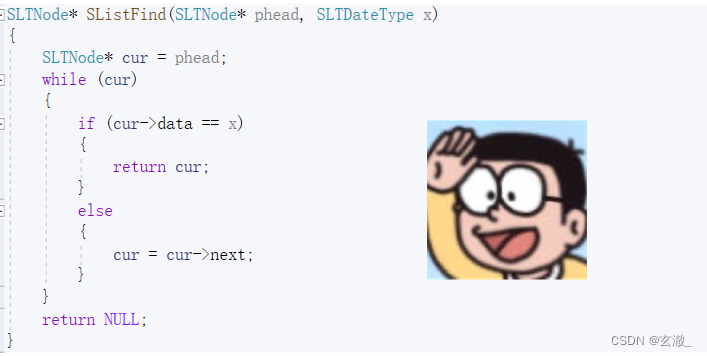
这是查找函数的主体，但是当链表中有多个相同的数据的时候，我们该如何一一查找出来呢？
如下图所示：
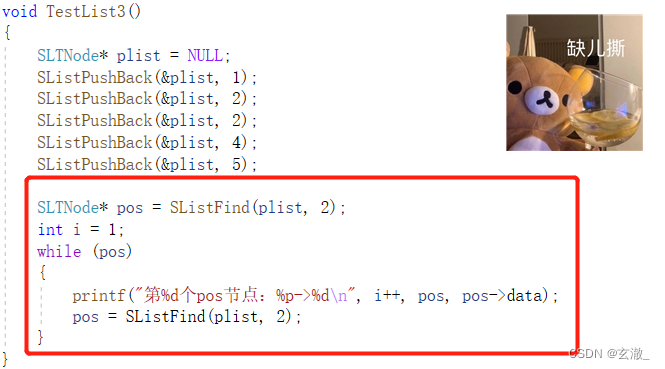
通过循环来实现相同数据的查找！💨💨
在指定位置插入元素函数
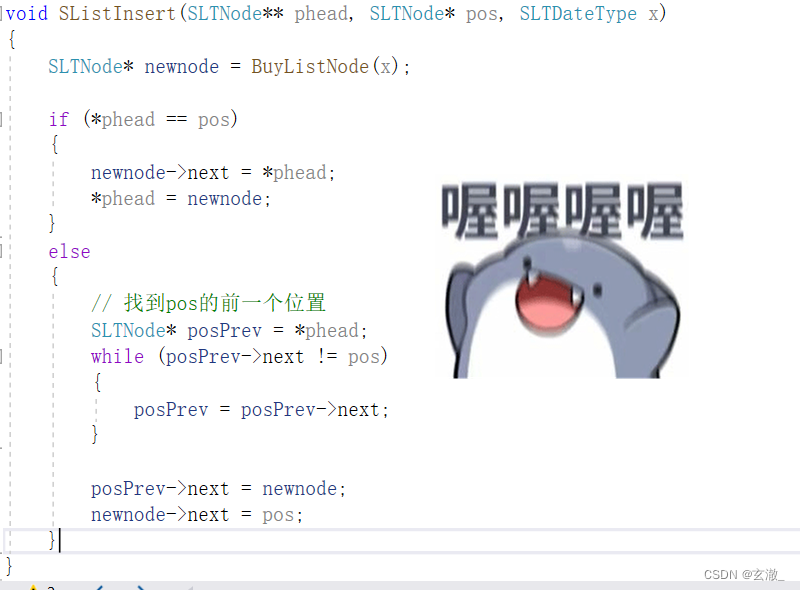
找到pos位置的前置元素，然后在prev的后面插入新的元素即可
但是通过实例可以发现，当我们要在第一个元素之前插入时，上述代码会运行出错，此时需要我们多一步判断操作（头插）
链表和顺序表的区别
顺序表
缺陷：
- 空间不够了，需要扩容，扩容是有消耗
- 头部或者是中间的位置的插入删除，需要挪动，挪动数据也是需要有消耗的
- 避免频繁扩容，一次一遍都是按照倍数去扩容（2倍），可能存在一定的空间浪费
优点：
- 可以使用下标来访问：a[i] 等价于 *(a + i)（支持随机访问）
链表
优点:
- 按需申请空间，不用了就释放空间（更合理地使用了空间）
- 头部或者是中间插入删除数据，不需要挪动数据（不存在空间浪费）
?缺点：
- 每一个数据，都需要存一个指针去链接后面的数据结点
- 不支持随机访问（用下标访问第 i 个）
单链表OJ题
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
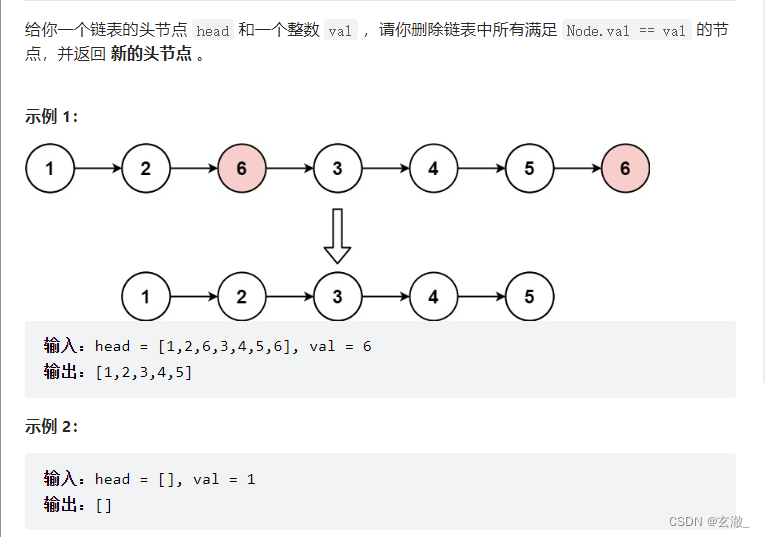
struct ListNode* removeElements(struct ListNode* head, int val){
if(head == NULL) return NULL;
struct ListNode* cur = head;
struct ListNode* prev = head;
while(cur != NULL)
{
if(cur->val == val)
{
// 删除
// 头删
if(cur == head)
{
head = cur->next;
free(cur);
cur = head;
}
else
{
prev->next = cur->next;
free(cur);
cur = prev->next;
}
}
else
{
// 迭代往后走
prev = cur;
cur = cur->next;
}
}
return head;
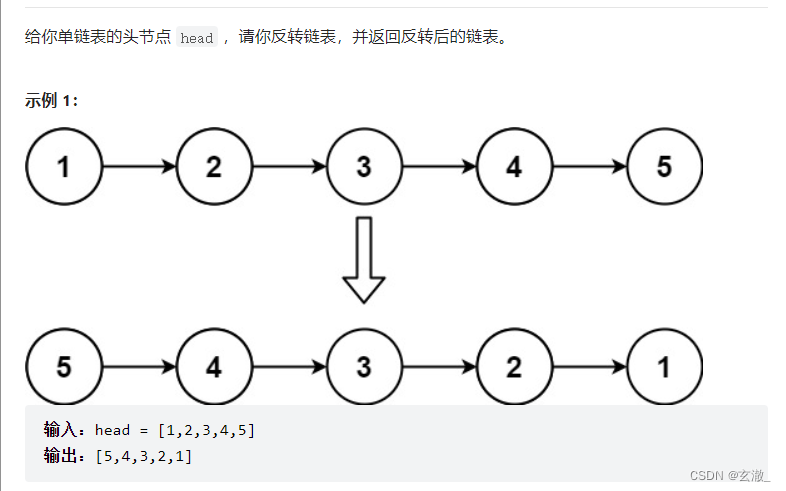
}LeetCode?206. 反转链表
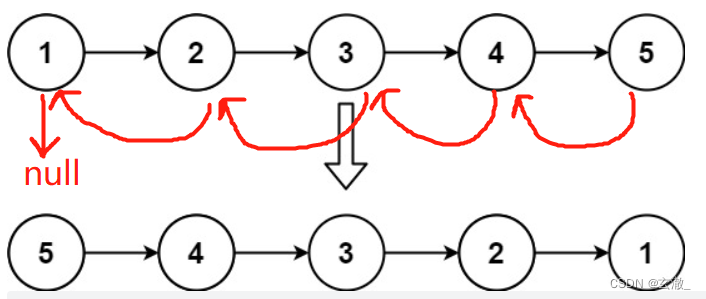?直接在原来的链表进行修改，修改每个结点的next指针
?需要定位指针来帮助我们定位地址
struct ListNode* reverseList(struct ListNode* head){
if(head == NULL) return NULL;
struct ListNode* n1, *n2, *n3;
n1 = NULL;
n2 = head;
n3 = head->next;
while(n2)
{
// 翻转
n2->next = n1;
// 迭代往后走
n1 = n2;
n2 = n3;
if(n3) n3 = n2->next;
}
return n1;
}头插法，不断取出新的元素头插到新链表中
struct ListNode* reverseList(struct ListNode* head){ struct ListNode* cur = head; struct ListNode* newhead = NULL; while(cur) { struct ListNode* next = cur->next; // 头插 cur->next = newhead; newhead = cur; // 迭代往后走 cur = next; } return newhead; }
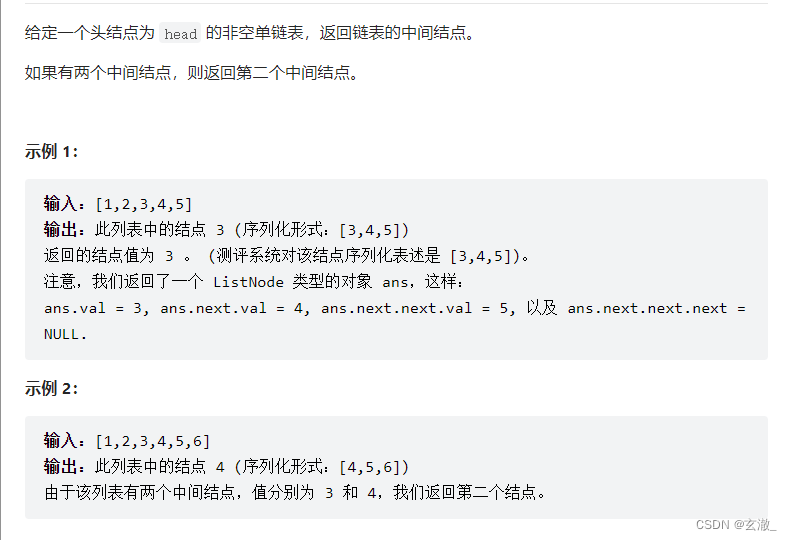
这道题可以用到经典的?“快慢指针”?算法
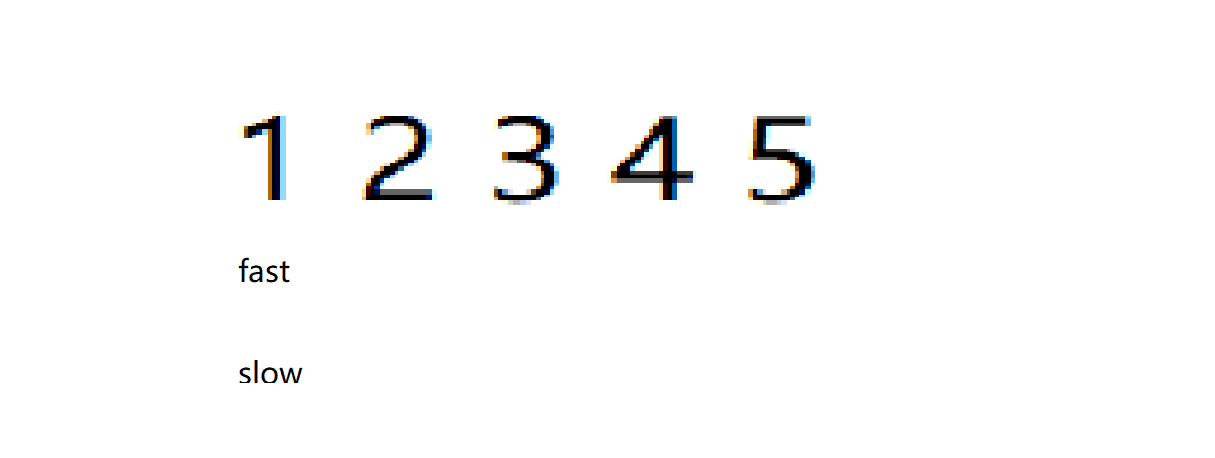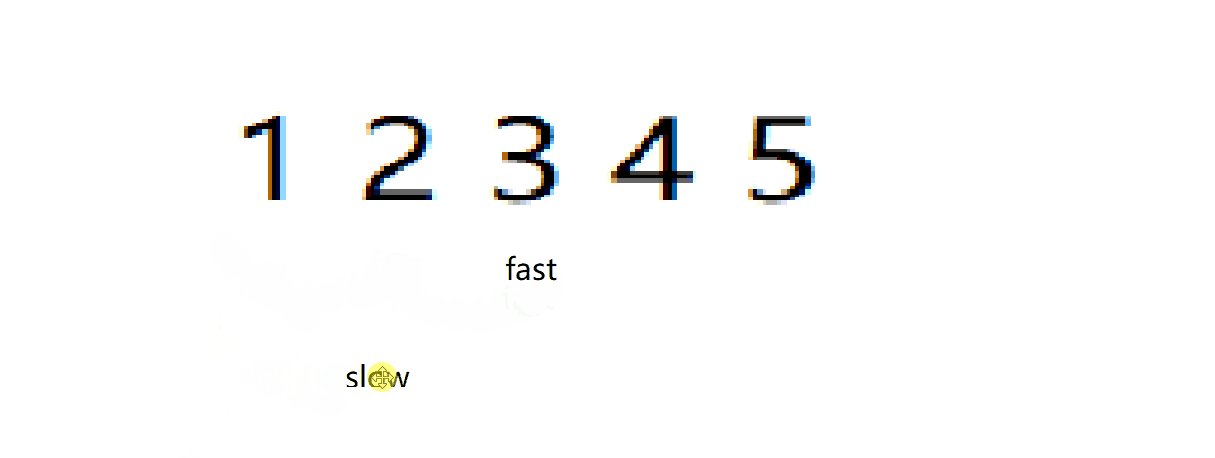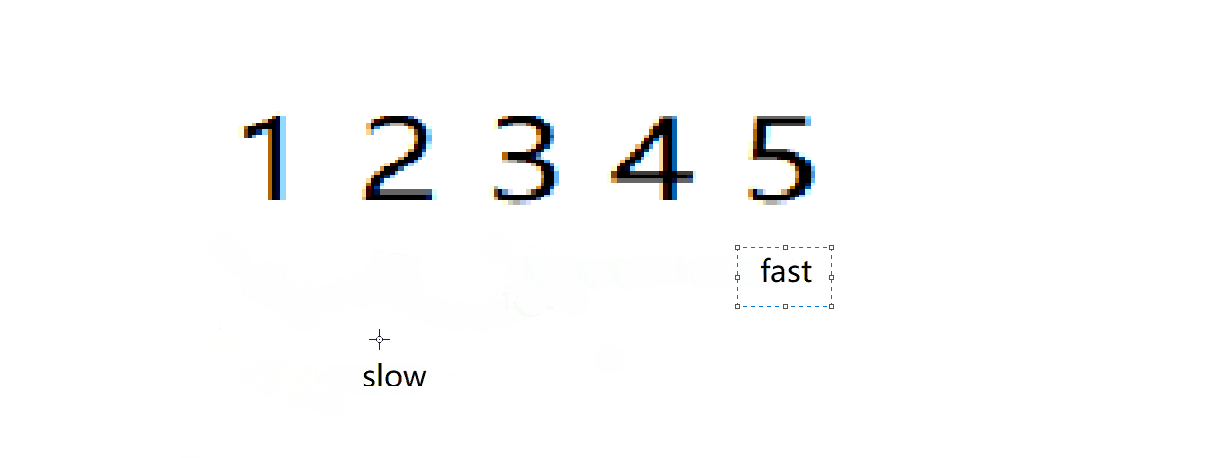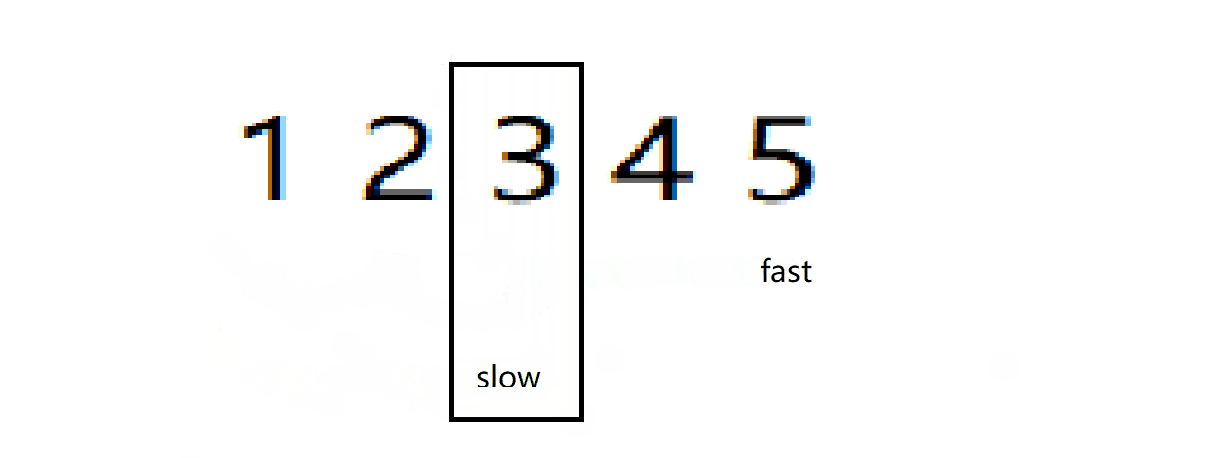
struct ListNode* middleNode(struct ListNode* head){
struct ListNode* slow, *fast;
slow = fast = head;
while(fast && fast->next)
{
slow = slow->next;
fast = fast->next->next;
}
return slow;
}
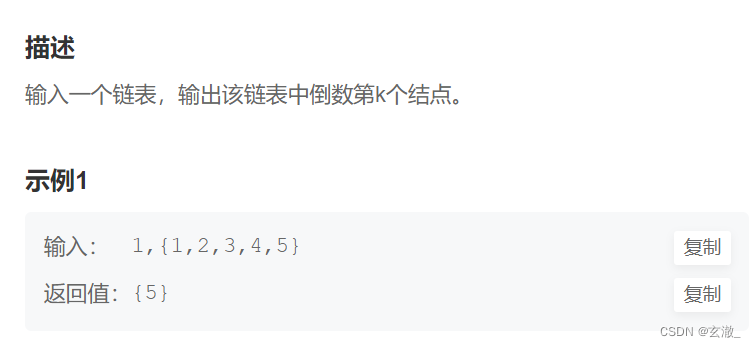
- fast 先走k步
- slow 和 fast 一起走，fast == NULL 时就是倒数第 k 个?
struct ListNode* FindKthToTail(struct ListNode* pListHead, int k ) { if(pListHead == NULL) return NULL; struct ListNode* fast, *slow; slow = fast = pListHead; while(k -- ) { if(fast == NULL) { return NULL; } fast = fast->next; } while(fast) { slow = slow->next; fast = fast->next; } return slow; }
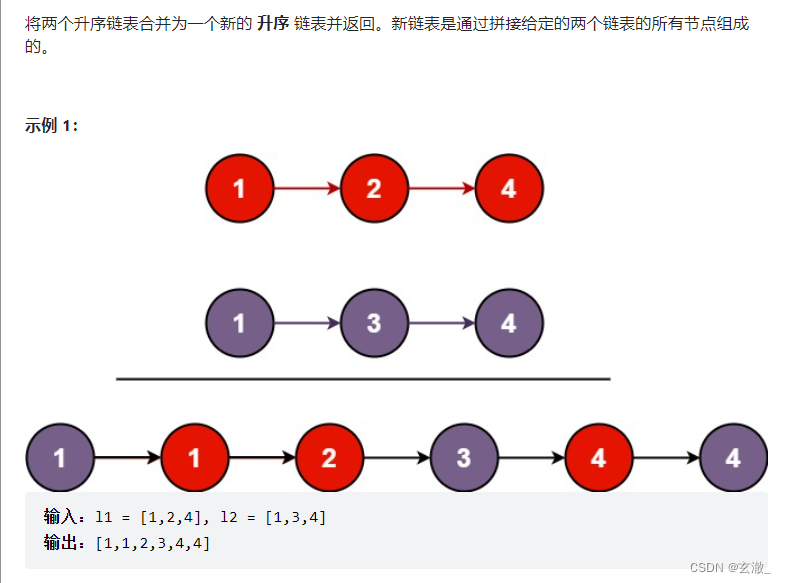
struct ListNode* mergeTwoLists(struct ListNode* l1, struct ListNode* l2){
if(!l1) return l2;
if(!l2) return l1;
struct ListNode* head = NULL, *tail = NULL;
while(l1 && l2)
{
if(l1->val < l2->val)
{
if(head == NULL)
{
head = tail = l1;
}
else
{
tail->next = l1;
tail = l1;
}
l1 = l1->next;
}
else
{
if(head == NULL)
{
head = tail = l2;
}
else
{
tail->next = l2;
tail = l2;
}
l2 = l2->next;
}
}
if(l1)
{
tail->next = l1;
}
if(l2)
{
tail->next = l2;
}
return head;
}
class Partition { public: ListNode* partition(ListNode* pHead, int x) { struct ListNode* lessHead, *lessTail, *greaterHead, *greaterTail; // 开一个哨兵位头结点，方便尾插 lessHead = lessTail = (struct ListNode*)malloc(sizeof(struct ListNode*)); lessTail->next = NULL; greaterHead = greaterTail = (struct ListNode*)malloc(sizeof(struct ListNode*)); greaterTail->next = NULL; struct ListNode* cur = pHead; while(cur) { if(cur->val < x) { lessTail->next = cur; lessTail = cur; } else { greaterTail->next = cur; greaterTail = cur; } cur = cur->next; } lessTail->next = greaterHead->next; greaterTail->next = NULL; return lessHead->next; } };
一种方法是利用前半个链表的元素之和减去后半个链表的元素之和，判断其是否为0
（要注意区分奇数情况和偶数情况）
class PalindromeList {
public:
bool chkPalindrome(ListNode* A) {
int count = 0;
int sum = 0;
struct ListNode* cur = A;
while(cur)
{
count ++ ;
cur = cur->next;
}
if(count % 2 == 0)
{
int k = 0;
cur = A;
while(cur)
{
k ++ ;
if(k <= count / 2) sum += cur->val;
else sum -= cur->val;
cur = cur->next;
}
if(sum == 0) return true;
else return false;
}
else
{
int k = 0;
cur = A;
while(cur)
{
k ++ ;
if(k == count / 2 + 1) ;
else if(k <= count / 2) sum += cur->val;
else if(k > count / 2 + 1) sum -= cur->val;
cur = cur->next;
}
if(sum == 0) return true;
else return false;
}
}
};?另外一种解法，是先找到链表的中间结点，然后将后半部分的链表逆置，然后与前半部分的链表一一对比
struct ListNode* middleNode(struct ListNode* head){
struct ListNode* slow, *fast;
slow = fast = head;
while(fast && fast->next)
{
slow = slow->next;
fast = fast->next->next;
}
return slow;
}
struct ListNode* reverseList(struct ListNode* head){
struct ListNode* cur = head;
struct ListNode* newhead = NULL;
while(cur)
{
struct ListNode* next = cur->next;
// 头插
cur->next = newhead;
newhead = cur;
// 迭代往后走
cur = next;
}
return newhead;
}
class PalindromeList {
public:
bool chkPalindrome(ListNode* A) {
struct ListNode* mid = middleNode(A);
struct ListNode* rHead = reverseList(mid);
struct ListNode* curA = A;
struct ListNode* curR = rHead;
while(curA && curR)
{
if(curA->val != curR->val)
{
return false;
}
else
{
curA = curA->next;
curR = curR->next;
}
}
return true;
}
};
思路1： 暴力求解（穷举法）?
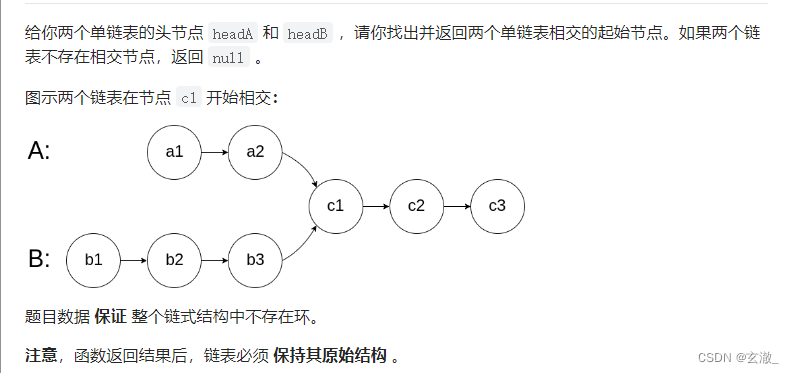
依次取出A链表中的每个结点跟B链表中的所有节点比较
如果有地址相同的点，就是相交，第一个相同的结点
思路2：
?的解法
1.尾结点相同就是相交
2.求交点：长的链表先走（长度差）步，再同时走，第一个相交的点就是交点
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) { struct ListNode* tailA = headA; struct ListNode* tailB = headB; int lenA = 0, lenB = 0; while(tailA->next) { tailA = tailA->next; lenA ++ ; } while(tailB->next) { tailB = tailB->next; lenB ++ ; } // 不相交 if(tailA != tailB) { return NULL; } // 长的先走差距步 int gap = abs(lenA - lenB); struct ListNode* longList = headA; struct ListNode* shortList = headB; if(lenA < lenB) { longList = headB; shortList = headA; } while(gap -- ) { longList = longList->next; } while(longList != shortList) { longList = longList->next; shortList = shortList->next; } return longList; }
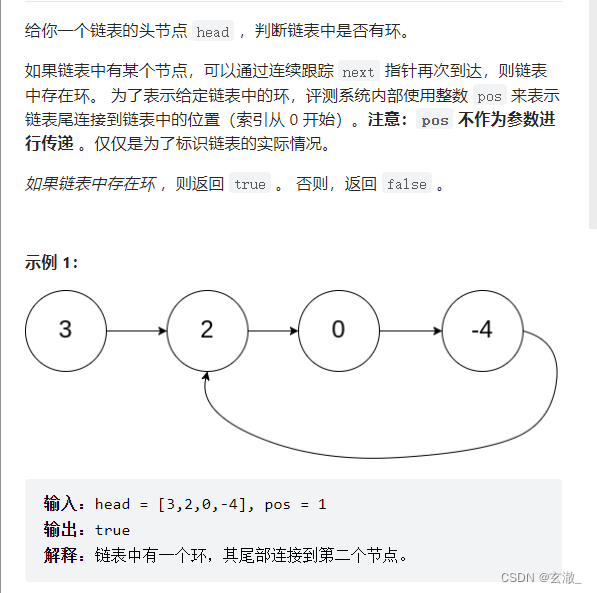
思路：【快慢指针】?
快慢指针，即慢指针一次走一步，快指针一次走两步，两个指针从链表其实位置开始运行，如果链表带环则一定会在环中相遇，否则快指针率先走到链表的末尾。
bool hasCycle(struct ListNode *head) {
struct ListNode* slow = head, *fast = head;
while(fast && fast->next)
{
slow = slow->next;
fast = fast->next->next;
if(slow == fast) return true;
}
return false;
}【拓展问题】
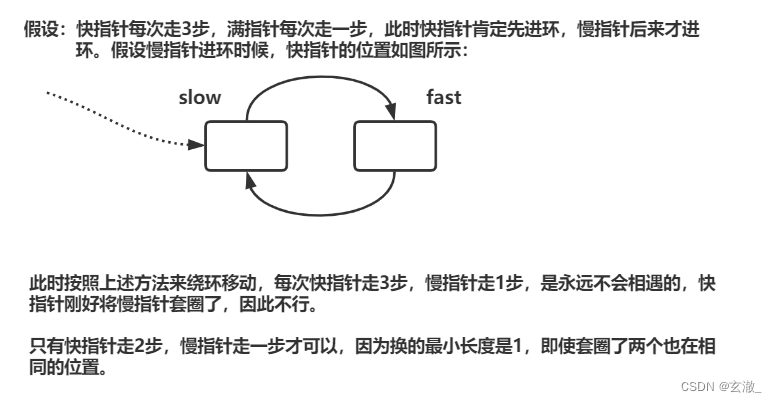
- 为什么快指针每次走两步，慢指针走一步可以？
- 假设链表带环，两个指针最后都会进入环，快指针先进环，慢指针后进环。当慢指针刚进环时，可能就和快指针相遇了，最差情况下两个指针之间的距离刚好就是环的长度。此时，两个指针每移动一次，之间的距离就缩小一步，不会出现每次刚好是套圈的情况，因此：在满指针走到一圈之前，快指针肯定是可以追上慢指针的，即相遇。
- 快指针一次走3步，走4步，...n步行吗？
- ?如果是距离是偶数的情况，差距为奇数步（如上图）则不会相遇
?
?
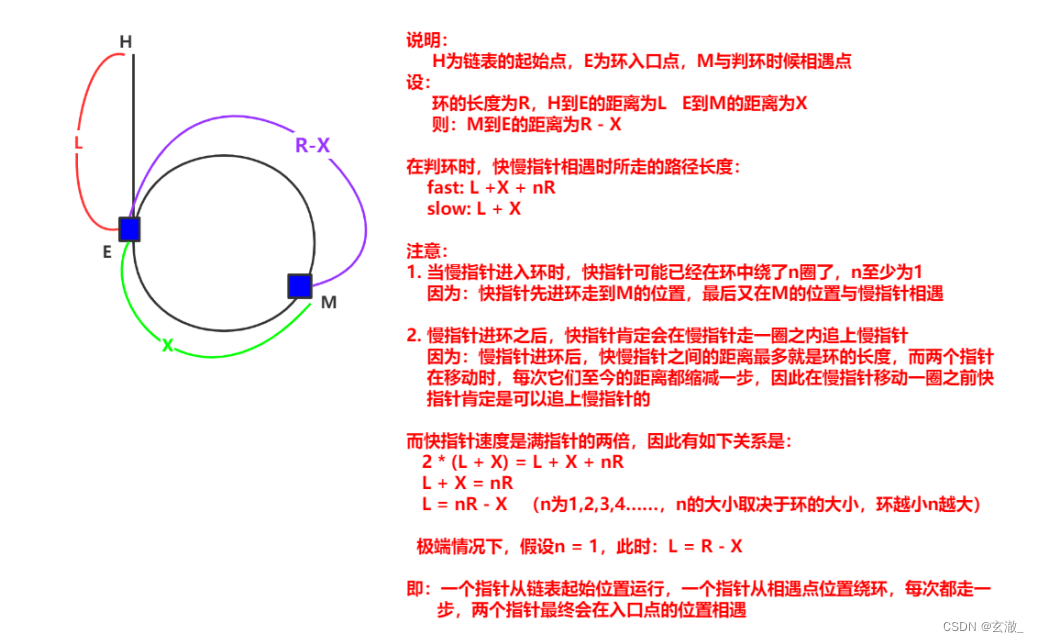
【结论】?
????????让一个指针从链表起始位置开始遍历链表，同时让一个指针从判环时相遇点的位置开始绕环运行，两个指针都是每次均走一步，最终肯定会在入口点的位置相遇。
【证明】???
struct ListNode *detectCycle(struct ListNode *head) {
struct ListNode* fast = head, *slow = head;
while(fast && fast->next)
{
slow = slow->next;
fast = fast->next->next;
if(slow == fast)
{
// 相遇
struct ListNode* meet = slow;
while(meet != head)
{
meet = meet->next;
head = head->next;
}
return meet;
}
}
return NULL;
}?