[数据结构与算法]322.零钱兑换·动态规划·背包问题

链接：https://leetcode.cn/problems/coin-change/solution/chun-c-by-xun-ge-v-4nmv/
来源：力扣（LeetCode）?

题目

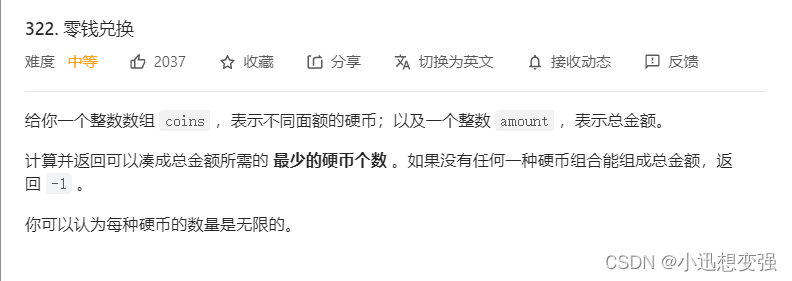
示例

思路

解题思路
1、确定状态
简单的说，就是解动态规划时需要开一个数组，数组的每个元素f[i]或者f[i][j]代表什么，类似解数学题中，xyz代表什么一样，具体分为下面两个步骤：
-------研究最优策略的最后一步
-------化为子问题
2、转移方程
根据子问题定义直接得到
3、初始条件和边界情况
初始条件一般都是a[0]、a[1]这种，多看看
边界条件主要是看数组的边界，数组越不越界
4、计算顺序
利用之前的计算结果

使用动态规划思路
我们定义一个dp数组，大小 amount+1 ,dp[i]表示整数金额 i 需要dp[i]个银币
所以dp[i] = dp[i - coins[j]] + 1 -> 表示当前金额 i 需要 i - coins[j]需要的银币加 1
所以遍历整个coins 更新dp[i] 寻找最小的银币数
在dp初始化时，我们将其附最大值，如果 dp[i - coins[j]] == 最大值，表示当前金额 i - coins[j] ，在coins中不存在 也保存最大值

代码

int cmp(const void * a, const void * b)
{
    return *(int *)a - *(int *)b;
}

#define MIN(a , b) ((a) < (b) ? (a) : (b))
int coinChange(int* coins, int coinsSize, int amount){
    qsort(coins, coinsSize, sizeof(coins[0]), cmp);//升序
    int dp[amount + 1];
    dp[0] = 0;
    for(int i = 1; i <= amount; i++)//遍历dp数组
    {
        dp[i] = amount + 1;//初始化最大值
        for(int j = 0; j < coinsSize; j++)//动态更新dp[i]
        {
            if(coins[j] > i)
            {
                break;
            }
            else
            {
                dp[i] = MIN(dp[i] , dp[i - coins[j]] + 1);
            }
        }
    }
    return dp[amount] == (amount+1) ? -1 : dp[amount];
}

时间空间复杂度