题目

在一个由 '0' 和 '1' 组成的二维矩阵内，找到只包含 '1' 的最大正方形，并返回其面积。

示例 1：

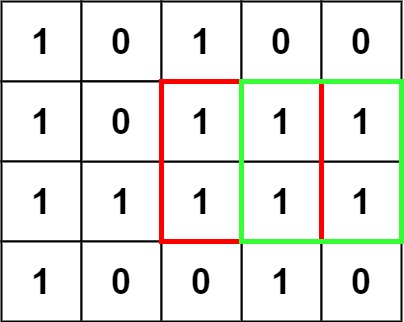
输入：matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出：4
示例 2：

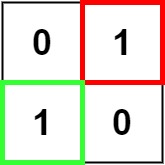
输入：matrix = [["0","1"],["1","0"]]
输出：1
示例 3：

输入：matrix = [["0"]]
输出：0
?

提示：

m == matrix.length
n == matrix[i].length
1 <= m, n <= 300
matrix[i][j] 为 '0' 或 '1'

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/maximal-square
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

1.暴力求解? ? ? ??

????????我一开始没有想到动态规划，只想到了暴力求解：就是依次扫每一个格子，看是否满足以它为正方形的左上角构成的最大正方形。

# 暴力解法：从可能的最大情况下，一个一个的去扫整个矩形
class Solution:
    def maximalSquare(self, matrix: List[List[str]]) -> int:
        m, n = len(matrix), len(matrix[0])  # m行n列
        max_len = min(m, n)  # 正方形的最大边为m，n中较小的一个值
        for cur_len in range(max_len, -1, -1):  # 当前正方形的边长
            i = 0
            while i <= m - cur_len:  # 垂直方向的移动
                j = 0
                next_i_len = cur_len
                while j <= n - cur_len:  # 水平方向的移动
                    next_j_len = 1
                    cur_square = matrix[i:i + cur_len]  # 当前正方形
                    for row_index in range(cur_len):
                        row = cur_square[row_index]
                        cur_row = row[j:j + cur_len]  # 当前正方形的每一行
                        flag = 0  # 用于判断要不要退出当前的外层循环(i层的)
                        for k in range(cur_len - 1, -1, -1):
                            if cur_row[k] == '0':  # 从每一行的最后一个数开始判断，只要等于0，就不能构成当前最大的正方形
                                next_j_len = max(next_j_len, k + 1)  # 计算下一步水平位移的增量，而不是每一次只增加1，这样节省了很多时间
                                flag = 1
                                break  # 因为不能构成当前最大的正方形，所以直接跳出循环(j层的)
                        if flag:
                            next_i_len = min(next_i_len, row_index + 1)  # 计算垂直方向的移动增量，而不是每一次只增1，这样子节省了很多时间
                            break  # 因为正方形中有0出现，所以也跳出i层循环
                    else:  # 如果当前的正方形都是由1组成的，则不会从上面的for循环由break跳出 那么当前的正方形就是面积最大的正方形，直接return即可
                        print(f'最长边:{cur_len}')
                        return cur_len ** 2

                    print(f'{next_i_len}*' * 100)
                    j += next_j_len  # 水平方向的移动
                i += next_i_len  # 垂直方向的移动

2.动态规划

? ? ? ? 后来看了题解后，可以用动态规划求解，与上面不一样的是，这里选一个点作为正方形的最右下角的那个顶点，然后在这个点上记录能够组成的最大的正方形的边，而它的取值和它自身是否为0有关；同时和它左边，上边和左上角的点的值有关，具体的状态转移方程如下：

# 假设dp[i][j]表示的以(i,j)为右下角的最大正方的边长
# 则dp[i][j]的值由其左边，上边和左上角的值共同确定

则dp[i][j]的值的确定可能出现两种情况：
    1.matrix[i][j]=0,则dp[i][j]直接等于0
    2.matrix[i][j]!=0,则比较其左边，上边和左上角的值，dp[i][j]=min(dp[i-1][j],dp[i][j-1],d[i-1][j-1])+1

# 动态规划求解
class Solution:
    def maximalSquare(self, matrix: List[List[str]]) -> int:
        m, n = len(matrix), len(matrix[0])
        dp = [[0 for j in range(n)] for i in range(m)]  # 初始化一个dp数组
        dp[0] = [int(i) for i in matrix[0]]  # 更新dp第一行的值，和matrix中第一行的值相同
        max_len = max(dp[0])  # 记录最长边
        if m > 1:
            for i in range(m):
                dp[i][0] = int(matrix[i][0])  # 更新dp第一列的值，和matrix中第一列的值相同
            dp[1][0] = int(matrix[1][0])
            max_len = max(max_len, dp[1][0])
            for i in range(1, m):
                for j in range(1, n):
                    if matrix[i][j] == '0':
                        dp[i][j] = 0
                    else:
                        dp[i][j] = min(int(dp[i - 1][j]), int(dp[i][j - 1]), int(dp[i - 1][j - 1])) + 1
                    max_len = max(max_len, dp[i][j])
        return max_len ** 2