一、题目

797. 所有可能的路径

给你一个有 n 个节点的有向无环图（DAG），请你找出所有从节点 0 到节点 n-1 的路径并输出（不要求按特定顺序）
graph[i] 是一个从节点 i 可以访问的所有节点的列表（即从节点 i 到节点 graph[i][j]存在一条有向边）。
示例 1：

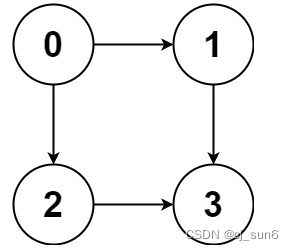
输入：graph = [[1,2],[3],[3],[]]
输出：[[0,1,3],[0,2,3]]
解释：有两条路径 0 -> 1 -> 3 和 0 -> 2 -> 3
示例 2：

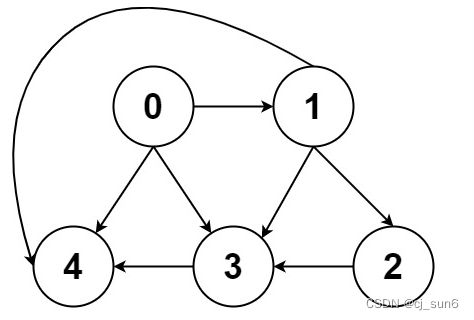
输入：graph = [[4,3,1],[3,2,4],[3],[4],[]]
输出：[[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]

二、思路

1、感觉属于一个比较简单的题目了，直接用DF是（深搜)就能做出来

2、主要是对题目的理解，题目读了很久没理解这个数组是啥意思，其实结合图就能看懂了，第i行表示的就是node i 可以到达其他node，Graph[i][j]就是node i可以到达node j。

三、代码

代码如下（示例）：

package leetcode.editor.cn;

import java.util.*;

/**
 * 所有可能的路径
 * @author CJ
 * @date 2022-07-15 15:35:21
 */
class P797_AllPathsFromSourceToTarget{
	 public static void main(String[] args) {
	 	 //测试代码
	 	 Solution solution = new P797_AllPathsFromSourceToTarget().new Solution();
	 }
	 
//力扣代码
//leetcode submit region begin(Prohibit modification and deletion)
class Solution {
	List<List<Integer>> res = new ArrayList<>();
	Stack<Integer> stack =new Stack<>();

	public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
		stack.add(0);
		dfs(graph, 0, graph.length - 1);
		return res;
	}
	public void dfs(int[][] graph, int x, int n) {
		if (x == n) {
			res.add(new ArrayList<>(stack));
			return;
		}
		for (int i = 0; i < graph[x].length; i++) {
			stack.add(graph[x][i]);
			dfs(graph, graph[x][i], graph.length - 1);
			stack.pop();
		}
	}
}
//leetcode submit region end(Prohibit modification and deletion)

}