一、二叉搜索树与双向链表

在这里插入图片描述

解法一:递归中序遍历(推荐)

创建表头head,指向当前节点的前指针pre
先递归到最左，初始化双向链表
处理中间根节点，连接pre与当前节点，pre再更新为当前节点
递归进入右子树，继续处理
节点为空时返回

class Solution {
public:
    TreeNode*head=NULL,*pre=NULL;//由于递归，这里设置在函数外
    TreeNode* Convert(TreeNode* pRootOfTree) {
        if(pRootOfTree==NULL)
            return NULL;
        Convert(pRootOfTree->left);//先递归到最左最小值
        if(pre==NULL)//初始化
        {
            head=pRootOfTree;
            pre=head;
        }
        else//双向链表的连接
        {
            pre->right=pRootOfTree;
            pRootOfTree->left=pre;
            pre=pRootOfTree;
        }
        Convert(pRootOfTree->right);//找最右
        return head;
    }
};

这里使用二叉树的结构实现的双向链表
时间复杂度:O(n),遍历二叉树所有节点
空间复杂度:O(n)，递归栈最大空间为n

解法二:非递归中序遍历

创建head头指针，指向当前节点的pre，以及标记是否第一次到最左的bool型变量
初始化一个栈用来辅助中序遍历
父节点入栈，进入二叉树最左端
第一次进入最左时要对head和pre初始化，然后用pre连接节点
最后右子树入栈

class Solution {
public:
    TreeNode* Convert(TreeNode* pRootOfTree) {
        if(pRootOfTree==NULL)
            return NULL;
        stack<TreeNode*>s;
        TreeNode*head=NULL,*pre=NULL;
        bool isfirst=true;//第一个遍历最左后置为假即可
        while(pRootOfTree!=NULL||!s.empty())
        {
            while(pRootOfTree!=NULL)//直到无左节点
            {
                s.push(pRootOfTree);
                pRootOfTree=pRootOfTree->left;
            }
            pRootOfTree=s.top();
            s.pop();
            if(isfirst)
            {
                pre=head=pRootOfTree;
                isfirst=false;
            }
            else
            {
                pre->right=pRootOfTree;
                pRootOfTree->left=pre;
                pre=pRootOfTree;
            }
            pRootOfTree=pRootOfTree->right;
        }
        return head;
    }
};

时间复杂度:O(n),遍历二叉树所有节点
空间复杂度:O(n)，栈最大空间为n

二、对称的二叉树

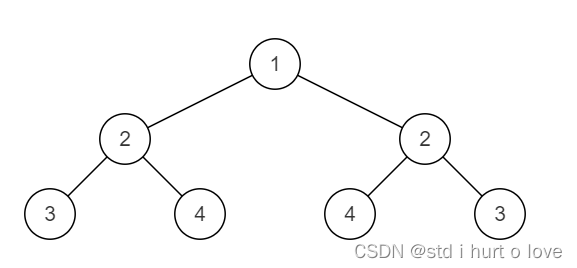
请添加图片描述
这就是一个对称的二叉树

解法一:递归(推荐)

利用前序遍历，如果对称，那么根左右与根右左的遍历节点值应当一样，同步遍历比较即可

进入子问题若两节点都为空，说明都到了叶子节点，且是同步的，返回true结束子问题，当只有一个节点为空或都不为空但值不相等，返回false结束子问题

class Solution {
public:
    bool recursion(TreeNode*p1,TreeNode*p2)
    {
        if(p1==NULL&&p2==NULL)
            return true;
        if(p1==NULL||p2==NULL||p1->val!=p2->val)
            return false;
        return recursion(p1->left, p2->right)&&recursion(p1->right, p2->left);
        //按各自顺序递归
    }
    bool isSymmetrical(TreeNode* pRoot) {
        return recursion(pRoot,pRoot);
    }
};

时间复杂度:O(n),n为二叉树节点数，本题相当于遍历整个二叉树两次
空间复杂度:O(n),递归栈最坏深度为n

解法二:层序遍历

对每层的节点值进行回文判断，借助队列

先判断节点是否为空，空直接对称
准备两个队列作为从左至右和从右至左遍历的辅助容器
每次从两队列分别取出一个节点，若都为空，暂时相等，进入下一轮判断，若一个为空或两节点值不等，则不对称，判断完后加入各自子节点
遍历结束都匹配，返回true

class Solution {
public:
    bool isSymmetrical(TreeNode* pRoot) {
        if(pRoot==NULL)
            return true;
        queue<TreeNode*>q1,q2;
        q1.push(pRoot->left);//初始化分的是两个叶子节点
        q2.push(pRoot->right);
        while(!q1.empty()&&!q2.empty())
        {
            TreeNode*left=q1.front(),*right=q2.front();
            q1.pop();
            q2.pop();
            if(left==NULL&&right==NULL)
                continue;//暂时相等，还要继续判断
            if(left==NULL||right==NULL||left->val!=right->val)
                return false;//不同返回false
            q1.push(left->left);//从左到右入队列
            q1.push(left->right);
            q2.push(right->right);//从右到左入队列
            q2.push(right->left);
        }
        return true;
    }
};

时间复杂度:O(n),遍历二叉树一遍
空间复杂度:O(n),两辅助队列最大空间为n

三、合并二叉树

解法一:递归前序遍历

同时遍历两个二叉树，进行值的相加

先判断两个树是否为空，若一个为空则返回另一个树，若两个都为空则返回空
采用前序遍历，将两节点相加值添加到新树中
两树同步进入左子树和右子树

class Solution {
public:
    /**
     * 
     * @param t1 TreeNode类 
     * @param t2 TreeNode类 
     * @return TreeNode类
     */
    TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {
        // write code here
        if(t1==NULL)
            return t2;
        if(t2==NULL)
            return t1;
        TreeNode*head=new TreeNode(t1->val+t2->val);//根左右的方式递归
        head->left=mergeTrees(t1->left, t2->left);
        head->right=mergeTrees(t1->right, t2->right);
        return head;
    }
};

时间复杂度:O(min(n,m)),m和n分别为两棵树的节点，当其中一个树访问完时便结束循环，故取较小值
空间复杂度:O(min(n,m)),递归栈深度同时间，取较小值

解法二:非递归层次遍历

使用三个辅助队列，两个用来分别记录两数层次节点，第三个记录合并后的节点
两数同步层次遍历，先将根节点入队列并合并
每次从队列弹出一个元素，分别判断二者左右子节点是否存在，存在则合并相加，存在一个则连接该存在节点，都不存在，连接NULL

class Solution {
public:
    TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {
        //若只有一个节点返回另一个，两个都为NULL自然返回NULL
        if (t1 == NULL)
            return t2;
        if (t2 == NULL)
            return t1;
        //合并根节点
        TreeNode* head = new TreeNode(t1->val + t2->val); 
        //连接后的树的层次遍历节点
        queue<TreeNode*> q; 
        //分别存两棵树的层次遍历节点
        queue<TreeNode*> q1; 
        queue<TreeNode*> q2;
        q.push(head);
        q1.push(t1);  
        q2.push(t2);
        while (!q1.empty() && !q2.empty()) {
            TreeNode *node = q.front(), *node1 = q1.front(), *node2 = q2.front();
            q.pop();
            q1.pop();
            q2.pop();
            TreeNode *left1 = node1->left, *left2 = node2->left, *right1 = node1->right, *right2 = node2->right;
            //两个左节点都存在
            if (left1 || left2) { 
                if (left1 && left2) {
                    TreeNode* left = new TreeNode(left1->val + left2->val);
                    node->left = left; 
                    //新节点入队列
                    q.push(left); 
                    q1.push(left1);
                    q2.push(left2);
                //只连接一个节点
                } else if (left1) 
                    node->left = left1;
                  else
                    node->left = left2;
            }
            if (right1 || right2) {
                //两个右节点都存在
                if (right1 && right2) { 
                    TreeNode* right = new TreeNode(right1->val + right2->val);
                    node->right = right;
                    //新节点入队列
                    q.push(right); 
                    q1.push(right1);
                    q2.push(right2);
                //只连接一个节点
                } else if (right1)  
                    node->right = right1;
                  else 
                    node->right = right2;
            }
        }
        return head;
    }
};