栈
1、设链表不带头结点且所有操作均在表头进行,则下列最不适合作为链栈的是()
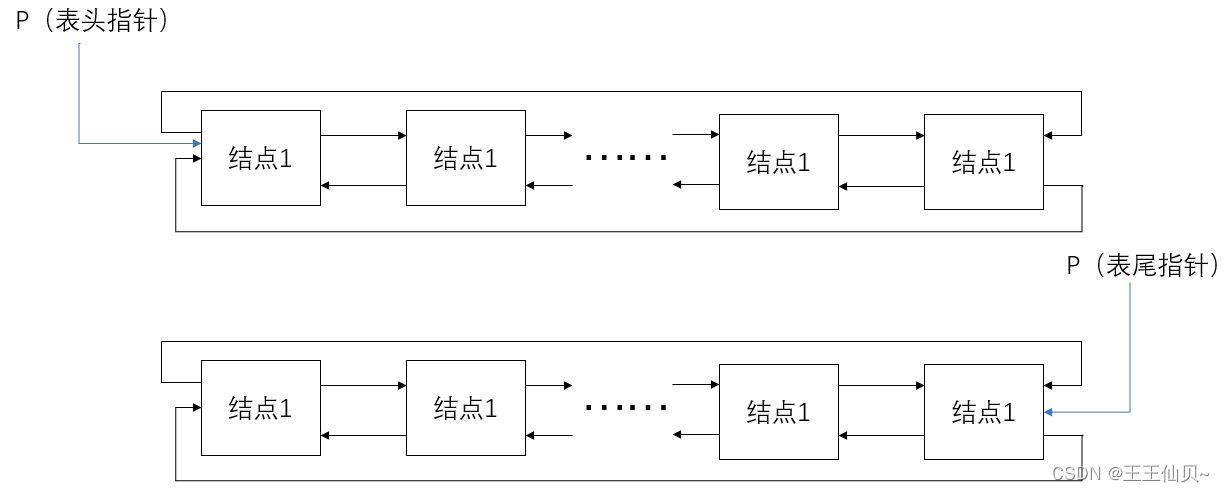
A、只有表头结点指针,没有表尾指针的双向循环链表
B、只有表尾结点指针,没有表头指针的双向循环链表
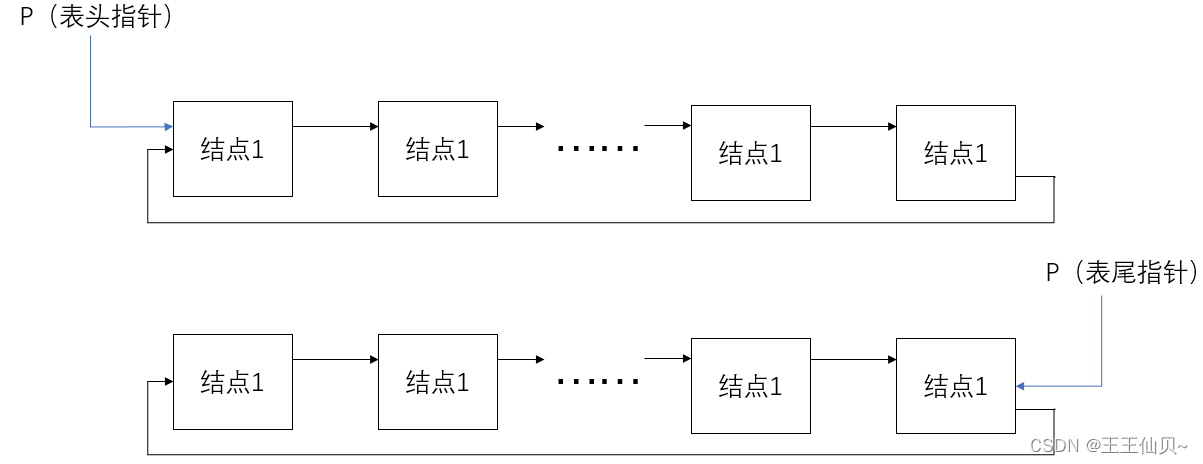
C、只有表头结点指针,没有表尾指针的单向循环链表
D、只有表尾结点指针,没有表头指针的单向循环链表
解析:选C
对于双向循环链表,找头结点和尾结点都很方便
对于单向循环链表,已知头结点,找尾结点需要遍历整个链表,已知尾结点找头结点很方便。在表头插入删除的时候,不仅要找到插入位置的下一个结点,也需要找到前一个结点,而C的情况,寻找前一个结点(即尾结点)需要遍历整个链表,非常耗时。而对于D,已知尾结点,插入位置的下一个结点即是尾结点指向的下一个节点,插入位置的前一个结点就是就是尾结点,因此十分方便。
2、采用共享栈的好处()
A、减少存取时间,降低发生上溢的可能
B、节省存储空间,降低发生上溢的可能
C、减少存取时间,降低发生下溢的可能
D、节省存储空间,降低发生下溢的可能
解析:选B
栈的存取时间复杂度都是O(1),因此不存在减少存取时间的问题。
如果栈的长度比较长,而0号栈数据又比较少,如果采用传统的栈,就会有浪费的情况,而如果使用共享栈,就可以再存储一个栈的数据,提高了存储空间的利用率,节省了存储空间。
上溢:栈顶发生溢出。例如:往栈里放入push()数据,栈已经满了,再继续放就会发生上溢。
下溢:栈底发生溢出。例如:从栈里取出pop()数据,栈已经空了,再继续取就会发生下溢。
共享栈只有在整个存储空间全部满了的时候才会发生上溢。一般情况下,如果0号栈数据比较多,那么1号栈就会相应地占用少一点的空间,两个栈会相互调节。因此相对来说,降低了发生上溢的可能。下溢与栈存储的数据数量以及pop()操作有关,和是不是共享栈没有太大关系。
3、下列关于栈的叙述中,错误的是()
a.采用非递归方式重写递归程序时必须要使用栈
b.函数调用时,系统要用栈保存必要的信息
c.只要确定了入栈次序,即可确定出栈次序
d.栈是一种受限的线性表,允许在其两端进行操作。
A、仅a
B、仅a、b、c
C、仅a、b、d
D、仅b、c、d
解析:选C
对于a,实现斐波拉契数列【F(0)=0,F(1)=1, F(n)=F(n - 1)+F(n - 2)(n ≥ 2,n ∈ N*)】迭代只需要一个循环即可,不需要使用栈。
对于b,函数调用的时候,系统需要记录当前执行到了哪一句,将该记录信息入栈,当函数调用结束后,再从上次执行的位置开始继续执行。
对于c,如果是按照1、2、3、4的顺序入栈,可以是1、2、3、4(1进1出,2进2出,3进3出,4进4出)的顺序出栈,也可以是4、3、2、1(1进,2进,3进,4进,4出,3出,2出,1出)的顺序出栈,出栈顺序取决于pop操作和push操作的顺序。
对于d,前半句正确,但是栈只允许在一端进行操作,队列是允许在两端进行操作。
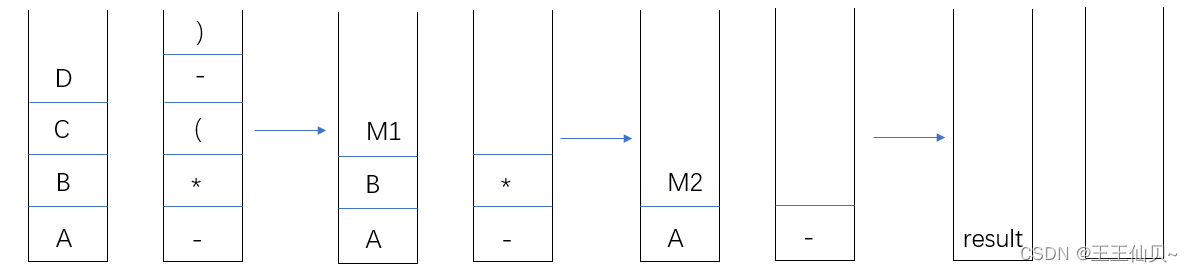
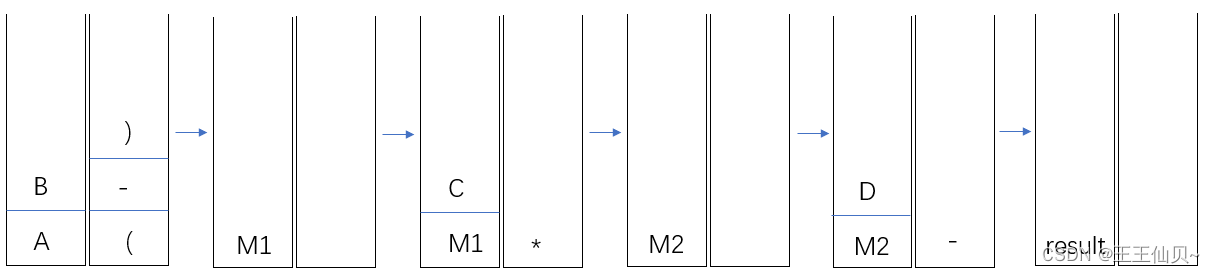
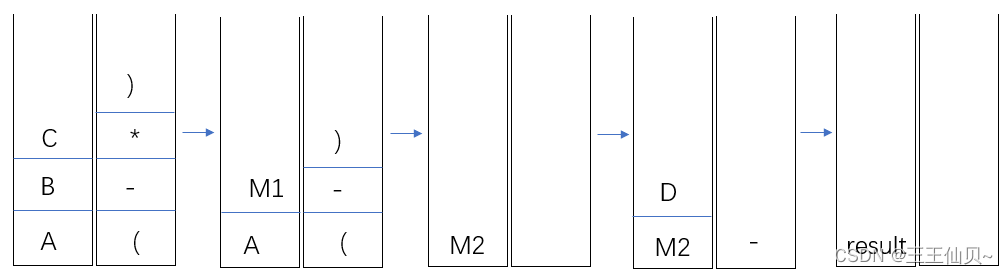
4、若栈S1中保存整数,栈S2中保存运算符,函数F()依次执行下述各步操作:
1)从S1中依次弹出两个操作数a和b。
2)从S2中弹出一个运算符op。
3)执行相应的运算b op a。
4)将运算结果压入S1中。
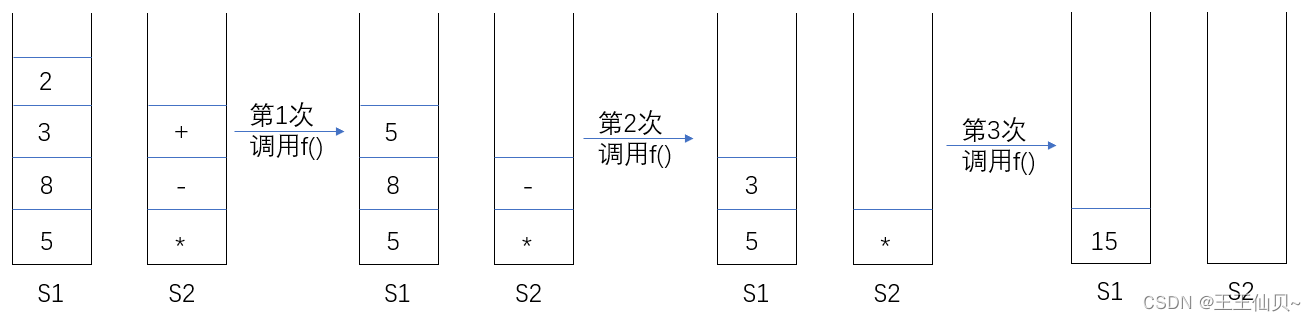
假定S1中的操作数依次是5,8,3,2(2在栈顶),S2中的运算符依次是*,-,+(+在栈顶)。调用三次F()后,S1栈顶保存的是()
A、-15
B、15
C、-20
D、20
解析:选B
注意!!!第三步是b op a,所以第二次调用的时候是8-5=3。
队列
1、允许对队列进行的操作有()
A、对队列中的元素排序
B、取出最近进队的元素
C、在队列元素之间插入元素
D、删除队头元素
解析:选D
队列允许先进先出,因此可以对队头进行删除访问等操作。
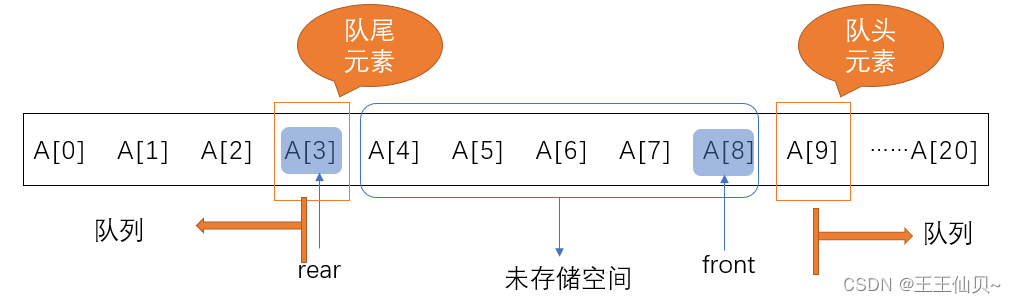
2、已知循环队列的存储空间为数组A[21],front指向队头元素的前一个位置,rear指向队尾元素,假设当前front和rear的值分别为8和3,则该队列的长度为()
A、5
B、6
C、16
D、17
解析:选C
队列长度为计算公式:(rear-front+maxsize)%maxsize=(3-8+21)%21=16。
front指向队头元素的前一个元素,rear指向队尾元素 与
front指向对头元素,rear指向队尾元素的下一个元素 的计算是相同的。
3、最适合用作链队的链表是()
A、带队首指针和队尾指针的循环单链表
B、带队首指针和队尾指针的非循环单链表
C、只带队首指针的非循环单链表
D、只带队首指针的循环单链表
解析:选B
带队首指针和队尾指针便可以直接找到队首队尾进行入队和出队操作,不用循环也可以,加上也行,但是相比非循环的来说会显得有点多余,有点大材小用,像是给了100个存储空间,但你只用了一个,当然是可以,但没必要。如果没有B选项,选A也可以。
带队首指针,可以直接找到队首,但是对于队尾,需要遍历整个链表。因为队利用链表存储时,不一定是头尾相接的,通过队首并不能直接找到队尾,往往是需要遍历链表来寻找队尾的。
4、已知循环队列存储在一维数组A[0…n-1]中,且队列非空时,front和rear分别指向队头元素和队尾元素。若初始时队列为空,且要求第一个进入队列的元素存储在A[0]处,则初始时front和rear的值分别是()
A、0,0
B、0,n-1
C、n-1,0
D、n-1,n-1
解析:选B
在执行入队操作时,rear指针先加1在将元素进行存储。因此(rear+1)%n=新元素加入的位置,A[++rear]=新元素的值。因此是(rear+1)%n=0,rear=n-1。
在入队操作时,front指针并不会发生改变,front要指向队首元素,在加入一个元素时,该元素即是队首元素,也是队尾元素,因此该元素加入后,rear=front,且根据题目,该元素存储在A[0]处,故front的值为0,在不进行出队操作前,front的值一直是0。
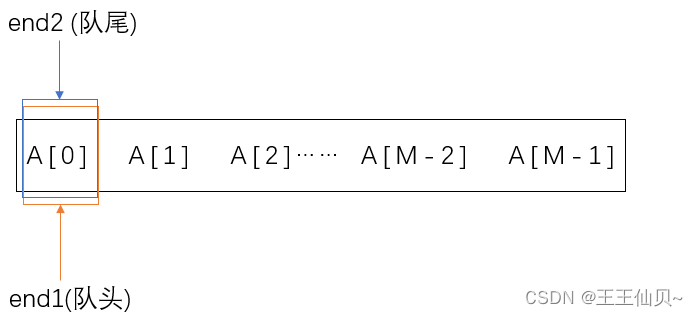
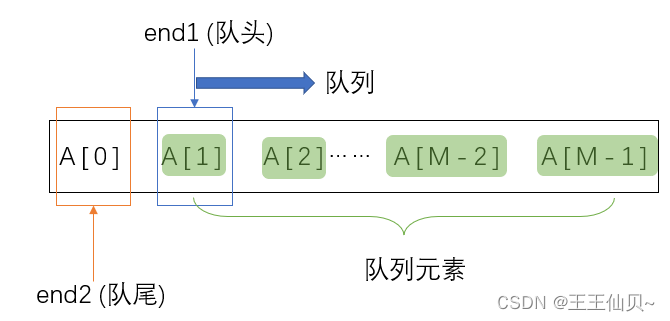
5、循环队列放在一维数组A[0…M-1]中,end1指向队头元素,end2指向队尾元素的后一个位置。假设队列两端均可进行入队和出队操作,队列中最多能容纳M-1个元素。初始时为空。下列判断队空和队满的条件中,正确的是()
A、队空:end1== end2; 队满:end1== (end2+1) mod M
B、队空:end1== end2; 队满:end2== (end1+1) mod (M-1)
C、队空:end2== (end1+1) mod M; 队满:end1== (end2+1) mod M
D、队空:end1== (end2+1) mod M; 队满:end2== (end1+1) mod (M-1)
解析:选A
end1== end2,队列为空。
end2== (end1+1) mod M,队列有一个元素。
end1== (end2+1) mod M,队列存储了M-1个元素,根据题干信息可知,队列最多存储M-1个元素,因此此时队满。
end2== (end1+1) mod (M-1),此时队列中有2个元素。
栈和队列的应用
1、利用栈求表达式的值时,设立运算数栈OPEN。假设OPEN只有两个存储单元,则在下列表达式中,不会发生溢出的是()
A、A-B * (C-D)
B、(A-B) * C-D
C、(A-B * C)-D
D、(A-B) * (C-D)
解析:选B
优先级:()> * > -。识别到左括号时,系统会期望收到右括号,并且当右括号出现时,会将左右括号之间的符号弹出,数据栈也相应地弹出数据进行计算。
在A中,OPEN至少需要4个存储单元
在B中,OPEN至少需要两个存储单元
在C中,OPEN至少需要两个存储单元
在D中,OPEN至少需要两个存储单元
2、执行函数时,其局部变量一般采用()进行存储
A、树形结构
B、静态链表
C、栈结构
D、队列结构
解析:选C
再调用函数的时候,系统会生成一个包含参数和返回变量的记录,并将该记录放入栈中,如果该函数有局部变量,也需要放入栈中,当函数调用完,则弹出栈,之后的程序不能再使用。
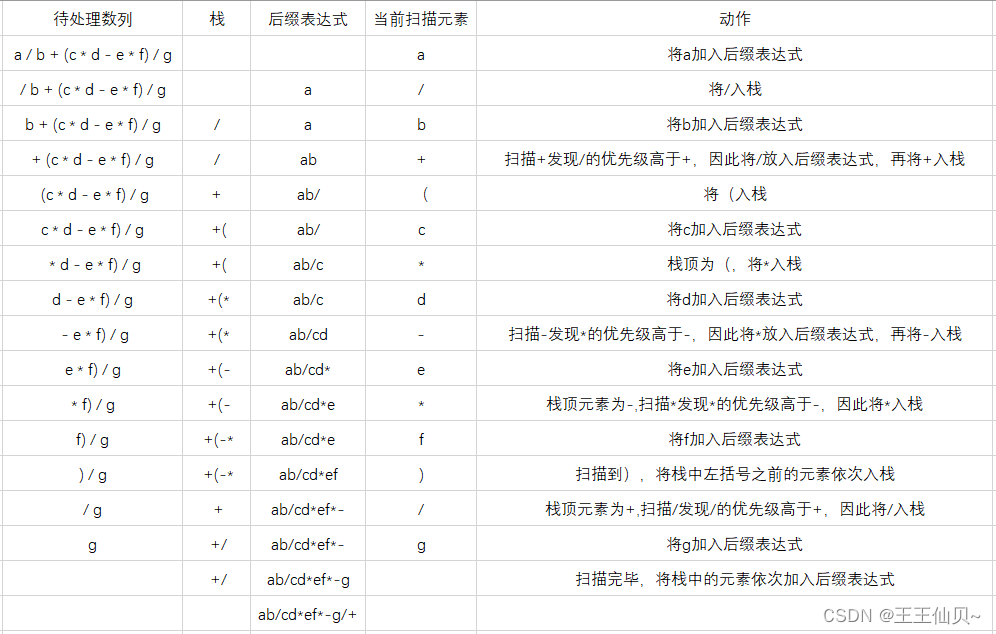
3、假设栈初始为空,将中缀表达式a / b + (c * d - e * f) / g转化为对应的后缀表达式的过程中,当扫描到 f 时,栈中的元素依次是()
A、+ ( * -
B、+ ( - *
C、/ + ( * - *
D、/ + - +
解析:选B
中继表达式转化为后继表达式的方法:从左到右依次扫描中继表达式,遇到数字就加入后继表达式,如果遇到运算符:1)遇到的是 ’ ( ’ ,则入栈;2)遇到的是 ’ ) ’ ,则将 ’ ( ’ 之前栈中的所有运算符依次加入后继表达式;3)遇到的是其他运算符,当优先级高于除了 ’ ( ’ 之外的栈顶运算符时,则直接入栈,否则从栈顶开始,依次弹出比当前运算符优先级高或相等的运算符,直到遇到优先级比当前运算符低或遇到 ’ ( ’ 。
4、已知程序如下:
int S(int n)
{ return (n<=0)?0:S(n-1) +n; }
void main()
{ cout<< S(1); }
程序运行时使用栈来保存调用过程的信息,自栈底到栈顶保存的信息依次对应的是()
A、main() -> S(1) -> S(0)
B、S(0) -> S(1) -> main()
C、main() -> S(0) -> S(1)
D、S(1) -> S(0) -> main()
解析:选A
先运行主程序main(),然后是其中的语句S(1),S(1)调用了函数,且n>1,所以需要执行S(n-1)+n即S(0)+1。
因为栈是先进后出,所以从栈底到栈顶依次是main() -> S(1) -> S(0)
数组和特殊矩阵
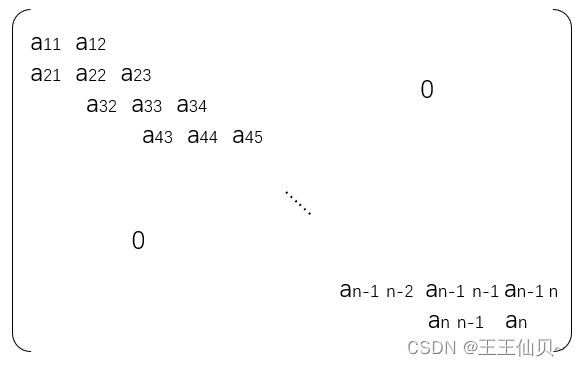
1、有一个100阶的三对角矩阵M,其元素mi,j,(1<=i,j<=100),按行优先依次压缩存入下标从0开始的一维数组N中,元素m30,30在N中的下标是()
A、86
B、87
C、88
D、89
解析:选B
第一行、最后一行只有两个元素,其余的行都有三个元素,因此对m30,30来说,有28行是有3个元素,其余的两行(第一行和m30,30所在的行)都是只有两个元素,因为是从0开始存储,所以要记得删掉1,所以是2+28*3+2-1=87
串
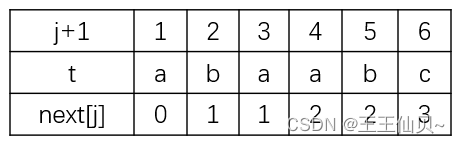
1、已知字符串S为‘abaabaabacacaabaabcc’,模式串t为’abaabc’。采用KMP算法进行匹配,第一次出现“失配”(s[i]!=s[j])时,i=j=5,则下次开始匹配时,i和j的值分别是()
A、i=1,j=0
B、i=5,j=0
C、i=5,j=2
D、i=6,j=2
解析:选C
采用KMP算法在出现失配时并不会直接回到最开始,而是要根据next数组进行移动。
因为题目中的i和j都是从0开始的,因此在计算next数组时,我们将j加1
因为在i=j=5处发生了失配,因此需要找模式串t中next[5]对应的值,为3,因此j需要移动到j+1=3处,即第三个字符处。此时j=2。而i则保持不变,因此i=5。