C语言经典题目练习2
一、二分法查找
一、什么是二分查找法?
对于二分查找法简单的来说就是在排好顺序的一组数据中,不断的进行对半分与我们要查找的元素进行比较。
二、算法思想
假设我们查找的元素Key与数组中间元素进行比较 (left 左边边界、right 右边边界、mid中间元素下标
1)key > arr[mid] ,则在arr数组后一半进行查找,left 变成mid +1
2)key < arr[mid] ,则在arr数组前一半进行查找,right变成mid-1
3)key = arr[mid],则结束运算
三、二分查找实例
现在有10个金币,当中有一个是假的,假金币的重量会比真金币的重要轻一点,现在有一个天平,请问最少需要比较多少次才可以找到这枚假金币?
思路:
1)将10枚金币分为两组,每组各5枚金币在一次称重中我们可以得出假金币的一组
2)将假金币的一组分成2 、2 、1将2 个金币的一组进行比较如果在2个金币的一组则再次比较就找到了假金币,如果在1个金币当中则不需在进行比较
3)在这题中最多需要查找3次,最少2次就可以找到
从上面的思想来看就是二分法的很好体现
二分查找demo测试
在使用二分法的关键点是我们要注意查找元素的边界
一般来说分为两种情况:左闭右闭[left,right] 、左闭右开[left,right)
情况一[left,right]
//情况一:左闭右闭 [left,right]
//二分查找函数 :查找成功返回查找下标,未找到返回-1
int Binary_Find(int arr[],int n,int value)
{
int mid = 0,left = 0,right = n - 1;
while(left <= right) //当左边大于右边结束循环
{
mid = (left + right)/2; //中间数
if(value < arr[mid]) //如果查找的数小于中间值
{
right = mid - 1;//改变右边的边界
}
else if(value > arr[mid]) //如果查找的值大于中间值
{
left = mid + 1; //改变左边的边界
}
else if(value == arr[mid])
{
//找到了该值 返回下标值
return mid;
}
}
return -1;
}
int main(void)
{
int i = 0;
int arr[] = {1,2,3,4,5,6,7,8,9};
int n = sizeof(arr)/sizeof(int); //数组总个数
int value = 0; //要查找的变量
printf("数组元素为:");
for(i = 0;i<n;i++)
{
printf("%d ",arr[i]);
}
printf("\n");
while(1)
{
printf("please input your num:");
scanf("%d",&value);
if(Binary_Find(arr,n,value))
{
printf("value exit in arr\n");
}
}
return 0;
}
情况二:[left,right)
//情况二:左闭右开[left,right)
//查找成功返回查找元素下标值,失败返回-1
int Binary_Find2(int arr[],int n,int value)
{
int left = 0,right = n,middle = 0;
while(left < right) //左闭右开注意边界条件不能取等
{
middle = (left + right)/2;
if(value < arr[middle]) //如果目标值小于arr[middle]
{
//更新左边区域的right值
right = middle;
}
else if(value > arr[middle])
{
//更新右边区域的left值
left = middle + 1;
}
else if(value == arr[middle]) //相等则找到了
{
return middle; //找到了返回下标值
}
}
return -1; //未找到返回-1
}
int main(void)
{
int i = 0;
int arr[] = {1,2,3,4,5,6,7,8,9};
int n = sizeof(arr)/sizeof(int); //数组总个数
int value = 0; //要查找的变量
printf("数组元素为:");
for(i = 0;i<n;i++)
{
printf("%d ",arr[i]);
}
printf("\n");
while(1)
{
printf("please input your num:");
scanf("%d",&value);
if(Binary_Find2(arr,n,value))
{
printf("value exit in arr\n");
}
}
return 0;
}

二、删除数组中元素
删除数组中某个元素并返回删除后的数组元素个数
思路:对于删除数组中的元素有多种方式,这里使用的是双指针的方式,快慢指针:快指针记录数组元素的值,慢指针记录数组元素的下标
双指针方式
#include <stdio.h>
//删除数组中某个元素并返回删除后元素的个数
int Delete_Element(int arr[],int n,int target)
{
int fast = 0,slow = 0; //使用双指针操作
//fast快指针表示数组元素的值
//slow慢指针表示数组元素值的下标
for(fast = 0;fast < n;fast++)
{
if(arr[fast] != target) //如果快指针的值不是我们的目标值
{
arr[slow++] = arr[fast]; //将该值赋值给新数组
}
}
return slow; //返回总个数
}
int main(void)
{
int arr[] = {1,4,2,8,6};
int n = sizeof(arr)/sizeof(int);
int res = 0,value = 0,i = 0;
printf("删除前数组元素个数为:%d\n",n);
printf("数组元素为:");
for(i = 0;i<n;i++)
{
printf("%d ",arr[i]);
}
printf("\nplease input target value:");
scanf("%d",&value);
res = Delete_Element(arr,n,value);
printf("\n删除后数组元素个数为:%d\n",res);
printf("数组元素为:");
for(i = 0;i<res;i++)
{
printf("%d ",arr[i]);
}
return 0;
}
三、有序数组的平方
将数组元素进行平方后升序排序(包含负数)
#include <stdio.h>
void Order_Array_Pow(int arr[],int n)
{
int result[sizeof(arr)/sizeof(int)] = {0}; //新数组元素个数
int i = 0,j = 0,k = n - 1; //k为新数组的最后一个下标
for(i = 0,j = n-1; i <= j;) //循环
{
if((arr[i] * arr[i]) > (arr[j] * arr[j]))
{
result[k--] = arr[i]*arr[i];
i++;
}
else
{
result[k--] = arr[j]*arr[j];
j--;
}
}
for(i =0;i<n;i++)
{
printf("%d ",result[i]);
}
printf("\n");
}
int main(void)
{
int arr[] = {-5,3,2,1,4};
int n = sizeof(arr)/sizeof(int);
Order_Array_Pow(arr,n);
return 0;
}
四、判断链表是否为环形链表
给定一个链表,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。

解题思路
1、判断该链表是否有环(快慢指针)
2、如何找到环的入口
可以使用快慢指针法,分别定义 fast 和 slow 指针,从头结点出发,fast指针每次移动两个节点,slow指针每次移动一个节点,如果 fast 和 slow指针在途中相遇 ,说明这个链表有环。
struct Node *DetectCycle(struct Node *head)
{
struct Node *fast = head; //快指针
struct Node *slow = head; //慢指针
//当快指针的值不为空并且下一个值不为空的时候
while(NULL != fast && NULL != fast->next)
{
fast = fast->next->next; //快指针一次移动两个节点
slow = slow->next; //慢指针一次移动一个节点
if(fast == slow) //如果快慢指针相遇
{
struct Node *index1 = fast; //index1为fast此时的索引
struct Node *index2 = head;//index2为slow指针索引(从Head开始)
while(index1 != index)
{
index1 = index1->next; //索引值后移
index2 = index2->next; //索引值后移
}
return index2; //返回环的入口
}
}
return NULL; //无环
}
五、删除链表倒数第N个节点
给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点
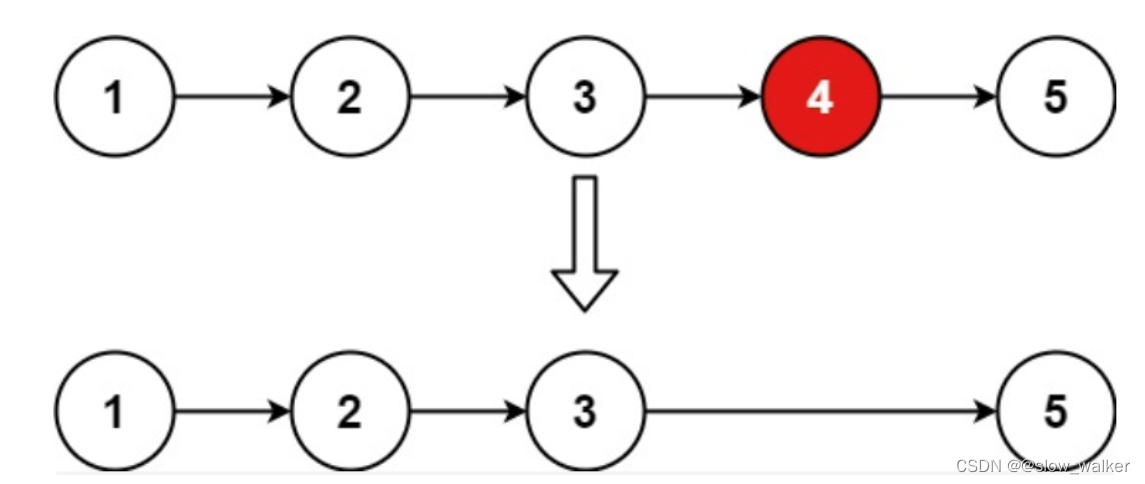
思路
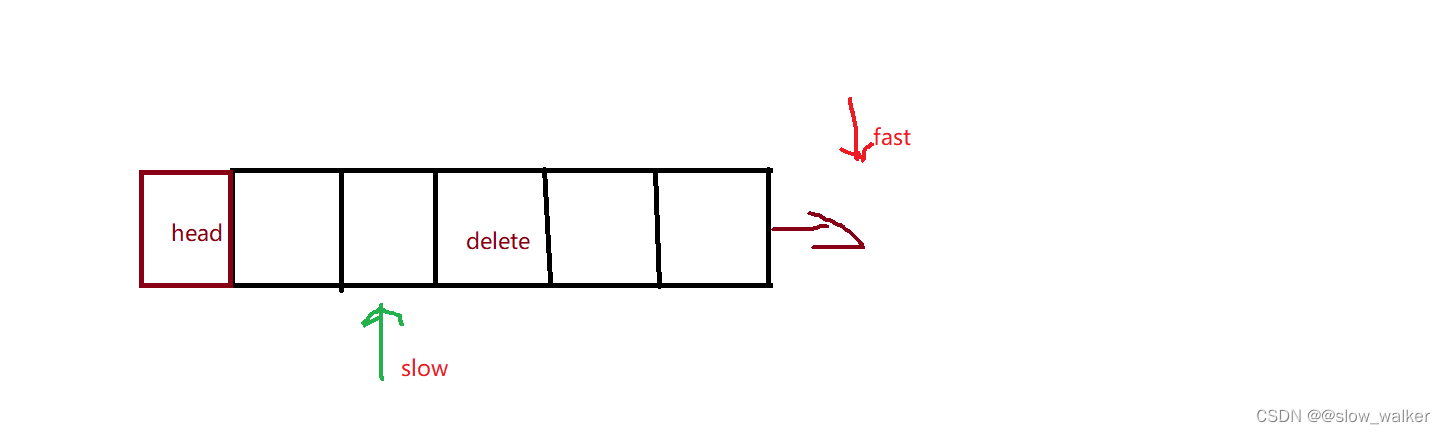
双指针的经典应用,如果要删除倒数第n个节点,让fast移动n步,然后让fast和slow同时移动,直到fast指向链表末尾。删掉slow所指向的节点就可以了,这里有一个小细节,我们要将快指针移n+1个节点,然后快慢指针在同时移动,这样的话慢指针刚好到我们要删除节点的前一个节点。
假设一共有6个节点,我们要删除倒数第3个也就是我们标记的delete节点,此时先让快指针一定N+1个节点也就是4个节点到delete后一个节点
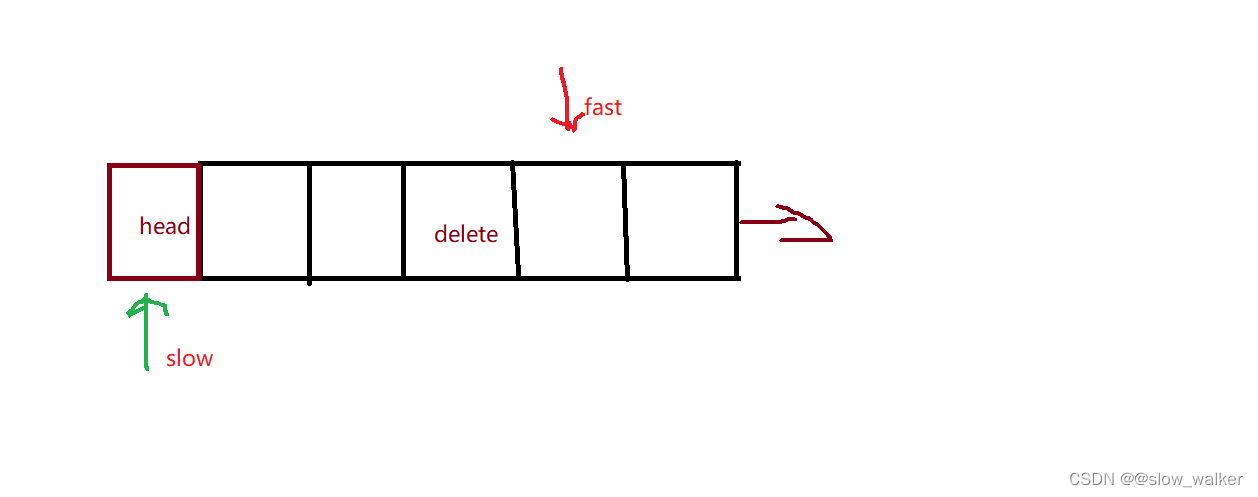
此时快慢指针同时移动,当fast指针为空时,slow指针的下一个就是要删除的节点
//带有头节点
struct Node *Delete_N_Node(struct Node *head,int n)
{
struct Node *fast = head; //快指针开始指向头节点
struct Node *slow = head; //慢指针开始指向头节点
while(n-- && fast!= NULL)
{
fast = fast->next;
}
fast = fast->next; //fast指针在提前走一步,让slow指针指向删除的上一个节点
while(NULL != fast)
{
slow = slow->next;
fast = fast->next;
}
slow->next = slow->next->next;
return head;
}