1.直接插入排序
依次将待排序的数插入到前面的有序子序列中

void InsertSort(int* arr, int n)
{
for (int i = 1; i < n; i++)
{
//一趟排序
int cur = i;//待排序数的下标
while (cur >= 0 && arr[cur] < arr[cur-1])
{
Swap(&arr[cur], &arr[cur-1]);
cur--;
}
}
}2.冒泡排序
依次比较相邻的两个数,将比较小的数放在前面,比较大的数放在后面(升序),直至全部排序完成。
void BubbleSort(int* arr, int n)
{
int exchange = 0;//记录单趟排序中是否发生交换,如果没有说明数组已有序,无需交换
for (int j = 1; j < n; j++)//n个数,需要n-1趟排序
{
//单趟排序
for (int i = 0; i < n - j; i++)
{
if (arr[i] > arr[i + 1])
{
Swap(&arr[i], &arr[i + 1]);
exchange = 1;
}
if (exchange == 0)
{
break;
}
}
}
}3.希尔排序
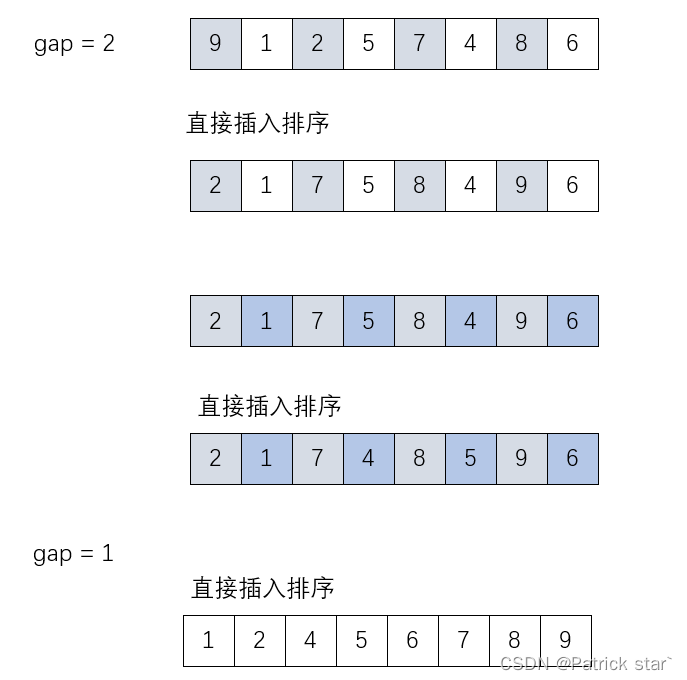
对于直接插入排序来说,如果待排序数组是基本有序的,那每次插入排序所需要的比较次数就会变少,因此希尔排序是在插入排序前进行预排序,使待排序数组基本有序,提升排序的效率。
预排序是将待排序数组,根据gap(每次gap的调整一般为gap = gap/3+1)的值分成若干个小数组,对小数组进行直接插入排序
希尔排序的实现有两种
第一种:
void ShellSort(int* arr, int n)
{
int gap = n;
int group = 0;
while (gap > 1)//gap大于1就进行预排序
{
group = 0;
gap = gap / 3 + 1;
while (group < gap)
{
int cur = 0;
while (cur < n)
{
for (int i = cur + gap; i > 0 && i < n; i -= gap)
{
if (arr[i] < arr[i - gap])
{
Swap(&arr[i], &arr[i - gap]);
}
}
cur += gap;
}
group++;
}
}
}?第二种:

void ShellSort(int* arr, int n)
{
int gap = n;
int group = 0;
int cur = 0;
while (gap > 1)//gap大于1就进行预排序
{
group = cur = 0;
gap = gap / 3 + 1;
while (group < n)
{
cur = group;
cur = cur+gap;
if (cur <n)
{
if (arr[cur] < arr[cur - gap])
{
Swap(&arr[cur], &arr[cur - gap]);
}
}
else
{
break;
}
group++;
}
}
}4.选择排序
遍历数组,每次选出最大(最小)的数放到最后(前)
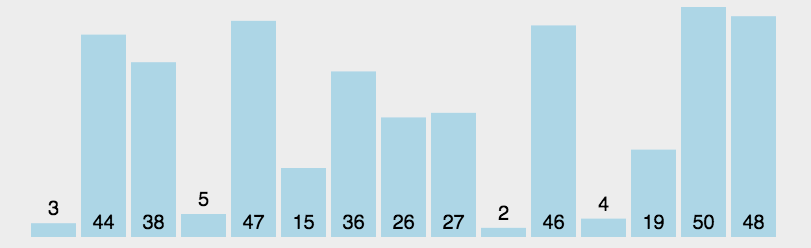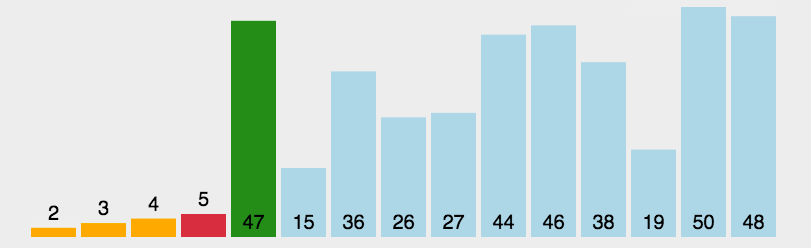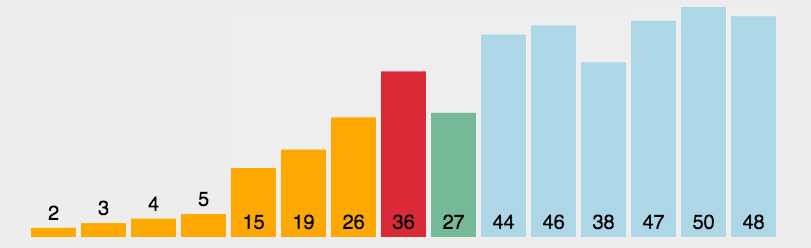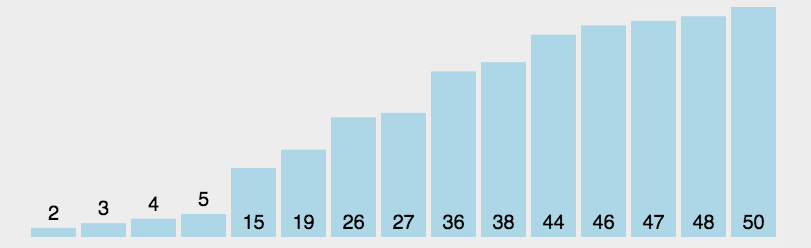
为了提高效率,每次遍历的时候可以同时选择最大和最小的数
void SelectSort(int* arr, int size)
{
int max = arr[0];
int min = max;
int maxIndex = 0;
int minIndex = 0;
int begin = 0;
int end = size - 1;
while (begin < end)
{
max = arr[begin];
maxIndex = begin;
min = arr[end];
minIndex = end;
//单趟排序
for (int i = begin; i <= end; i++)
{
if (arr[i] < min)
{
min = arr[i];
minIndex = i;
}
if (arr[i] > max)
{
max = arr[i];
maxIndex = i;
}
}
Swap(&arr[begin], &arr[minIndex]);
if (maxIndex == begin)//交换最小值的时候,把max覆盖掉了
{
Swap(&arr[end], &arr[minIndex]);
}
else
{
Swap(&arr[end], &arr[maxIndex]);
}
begin++;
end--;
}
}
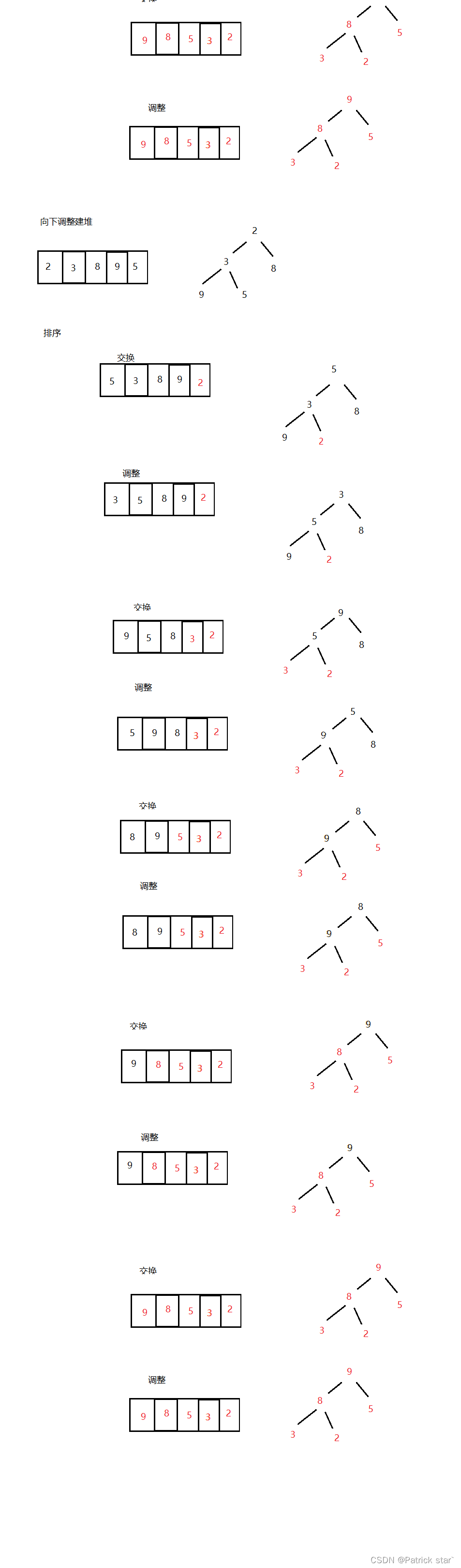
5.堆排序
利用大(小)根堆,依次选出最大(小)的数
void AdjustUp(int* p, int child)
{
assert(p);
int parent = (child - 1) / 2;
while (child > 0)
{
if (p[parent] > p[child])
{
Swap(&p[parent], &p[child]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
void AdjustDown(int* p, int size, int parent)
{
assert(p);
int child = parent * 2 + 1;
while (child < size)
{
if (child + 1 < size && p[child + 1] < p[child])//右孩子小于左孩子
{
child++;
}
if (p[child] < p[parent])
{
Swap(&p[child], &p[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
void HeapSort(int* p, int size)
{
assert(p);
向上调整建堆
//for (int i = 1; i < size; i++)
//{
// AdjustUp(p, i);
//}
//向下调整建堆
for (int i = (size - 1 - 1) / 2; i >= 0; i--)//从最后一个父节点开始调
{
AdjustDown(p, size, i);
}
//降序
while (size > 0)
{
Swap(&p[0], &p[size - 1]);
size--;
AdjustDown(p, size, 0);
}
}
6.快速排序
每趟排序,选择一个key,将小于key的放右边,大于key的放左边,然后再对key的左右两边进行相同的操作,直到完成排序。
hoare:
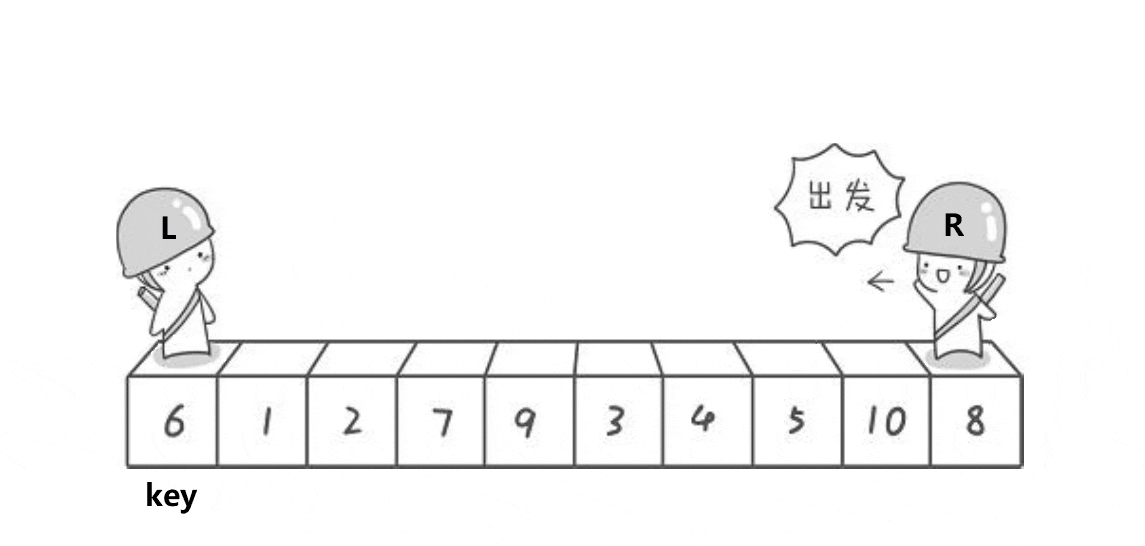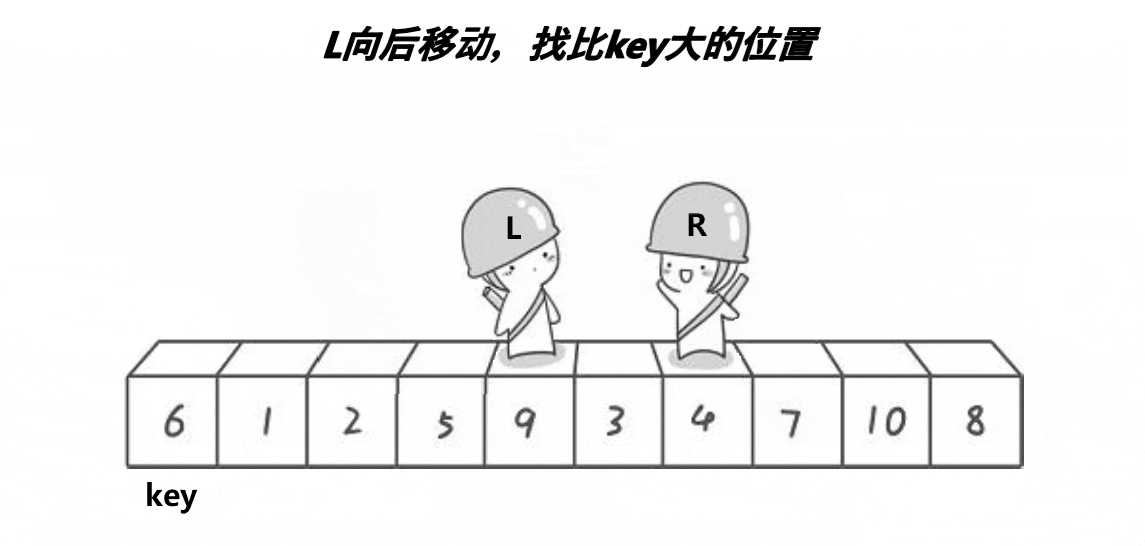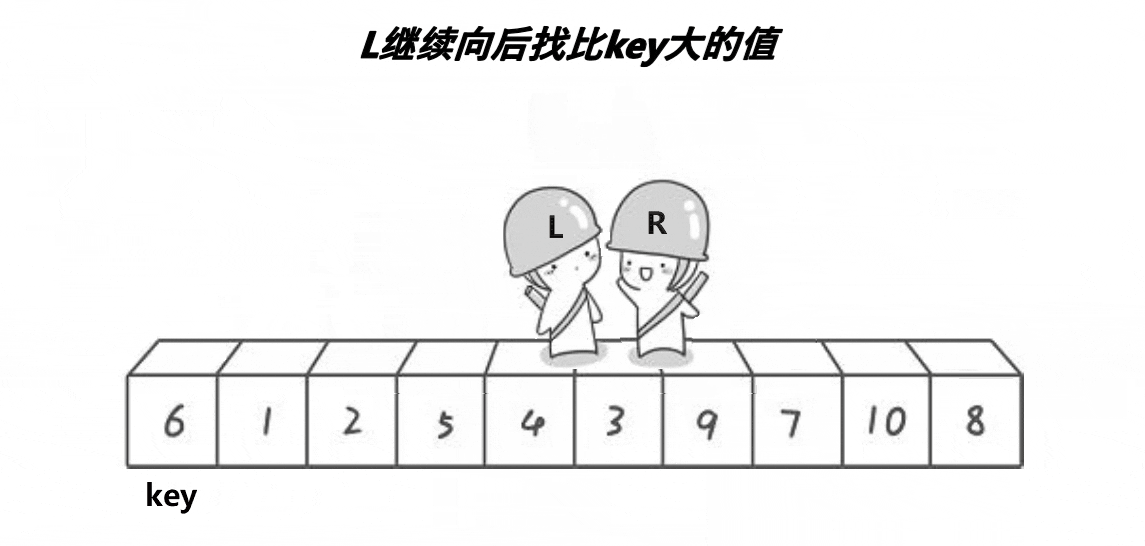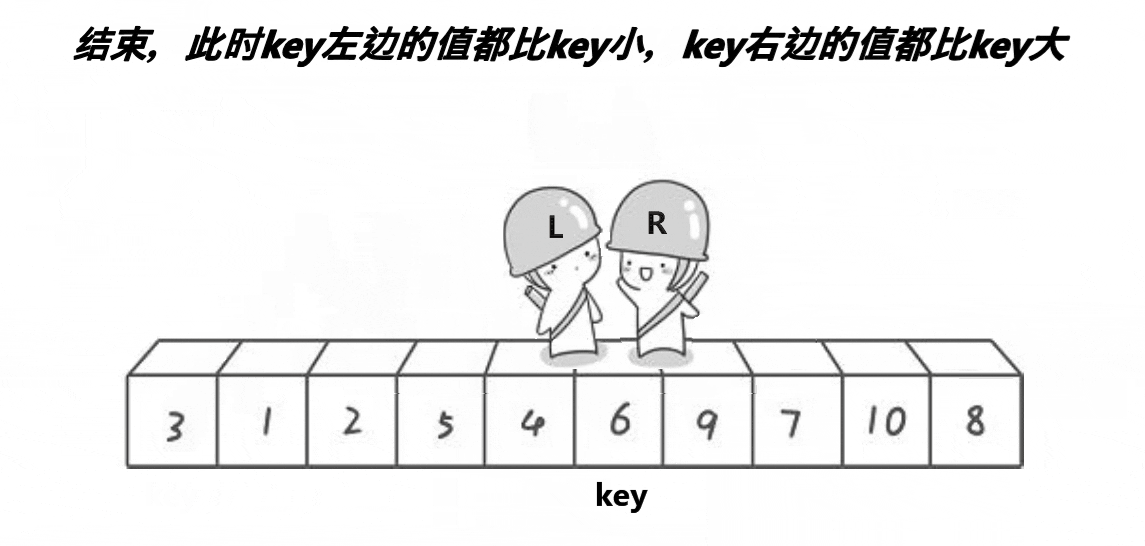
hoare法需要注意的是,当key取最左边的数时,需要R先走,使每次停下来的位置都小于key。而key取最右边时,需要L先走,时每次停下来的位置都大于key
//hoare
int PartSort1(int* arr, int left, int right)
{
int keyi = left;
while (left < right)
{
while (arr[right] > arr[keyi])//让right停在小于key的位置上
{
right--;
}
while (arr[left] < arr[keyi])//让left停在大于key的位置上
{
left++;
}
Swap(&arr[left], &arr[right]);
}
Swap(&arr[keyi], &arr[right]);
return right;
}
void QuickSort1(int* arr, int begin,int end)
{
if (begin >= end)
{
return;
}
int keyi = PartSort1(arr, begin, end);
QuickSort1(arr, begin, keyi-1);
QuickSort1(arr, keyi+1, end);
}挖坑法:
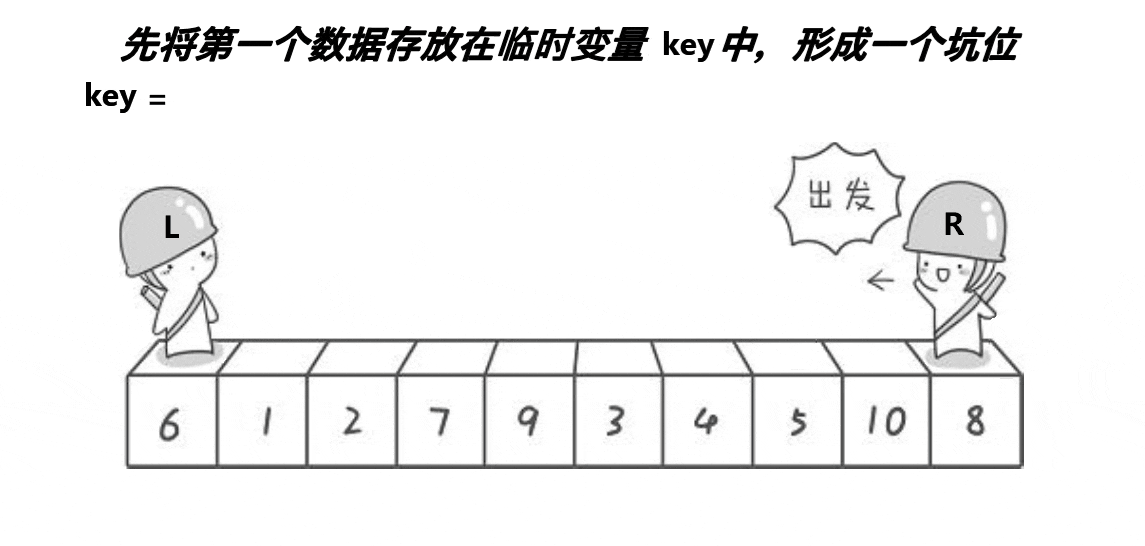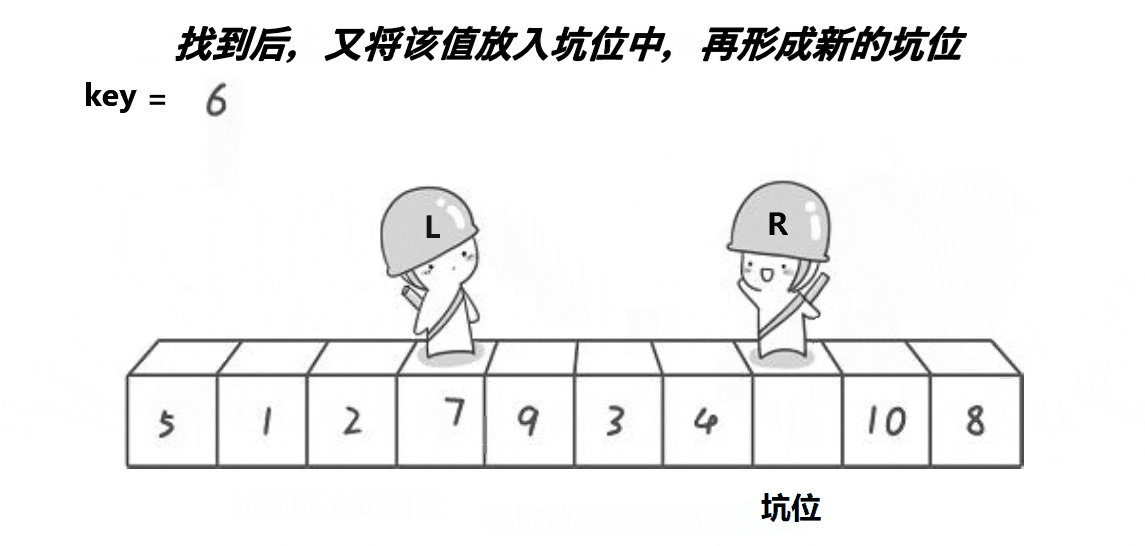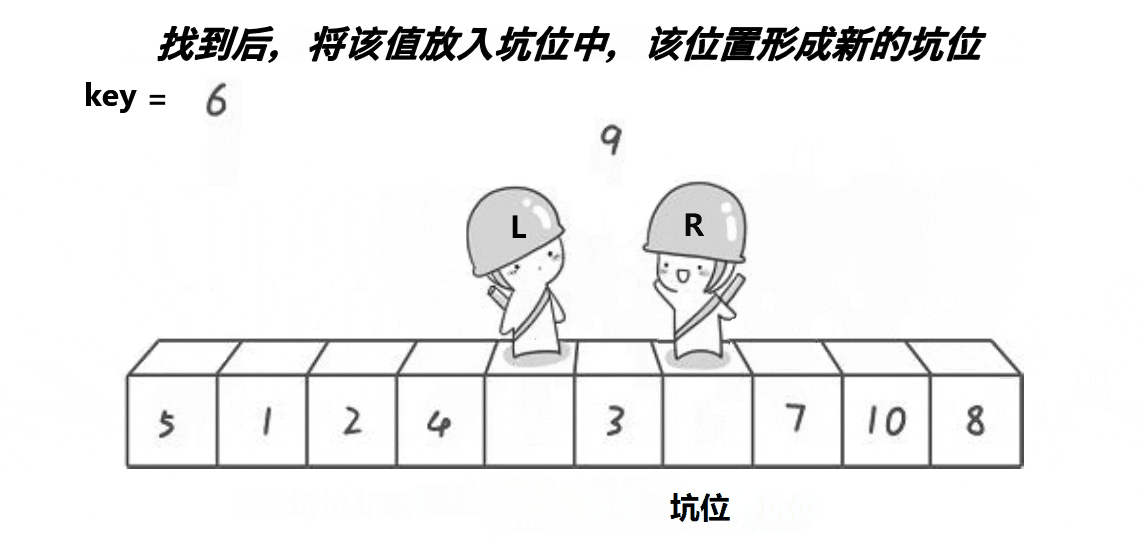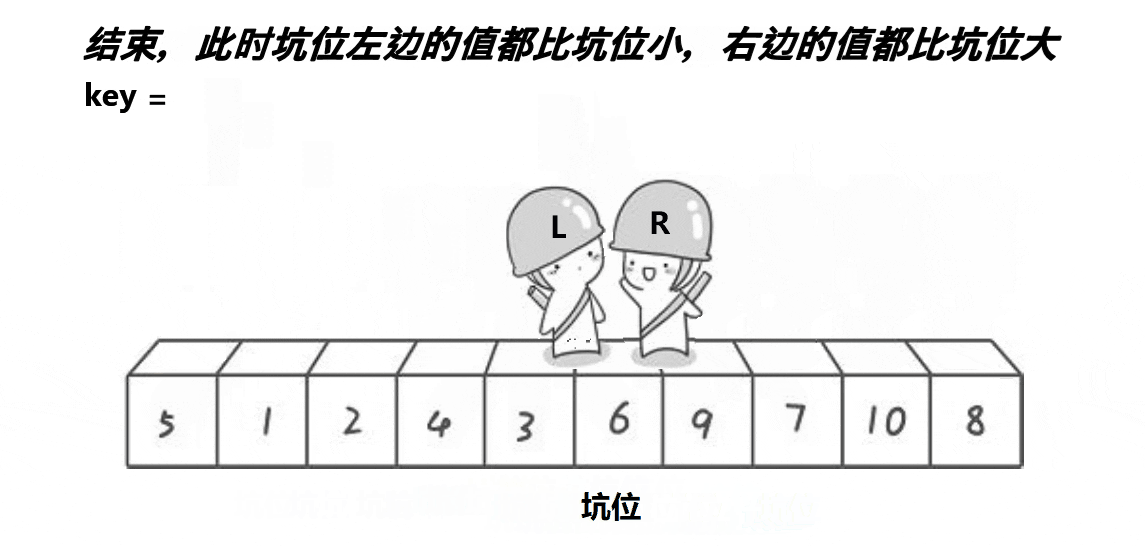
相比hoare法,挖坑法就不用规定谁先走谁后走
int PartSort2(int* arr, int left, int right)
{
int keyi = left;
int temp = arr[keyi];
int pit = left;
while (left < right)
{
while (left < right && arr[right] >= temp)
{
right--;
}
arr[pit] = arr[right];
pit = right;
while (left < right && arr[left] <= temp)
{
left++;
}
arr[pit] = arr[left];
pit = left;
}
arr[pit] = temp;
return pit;
}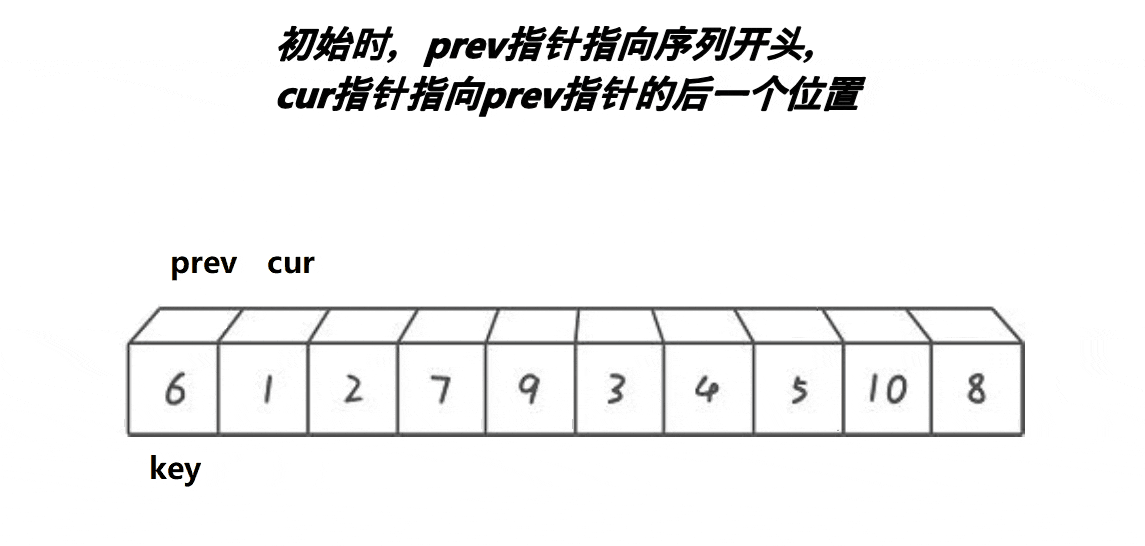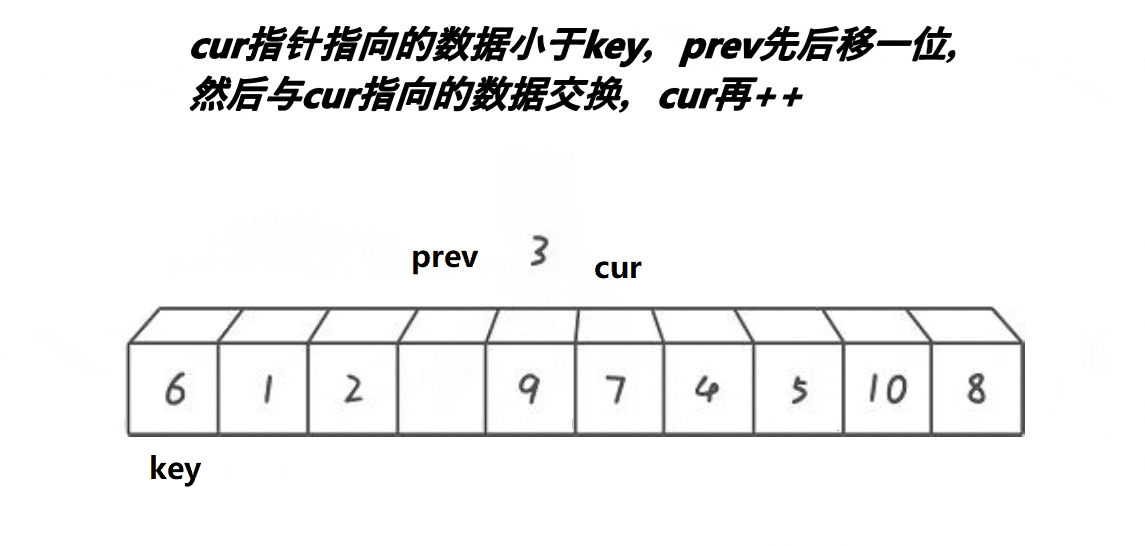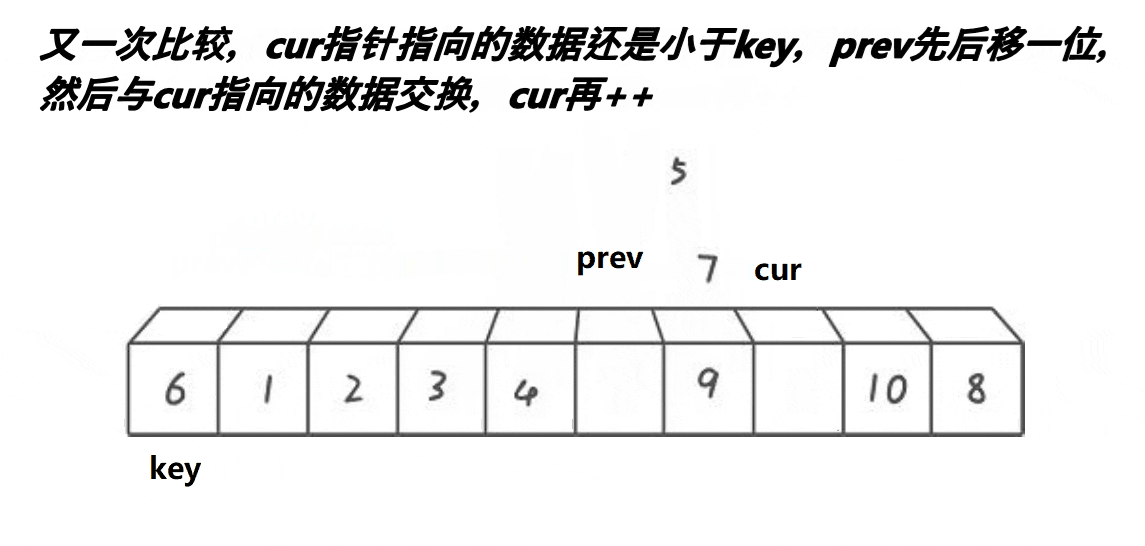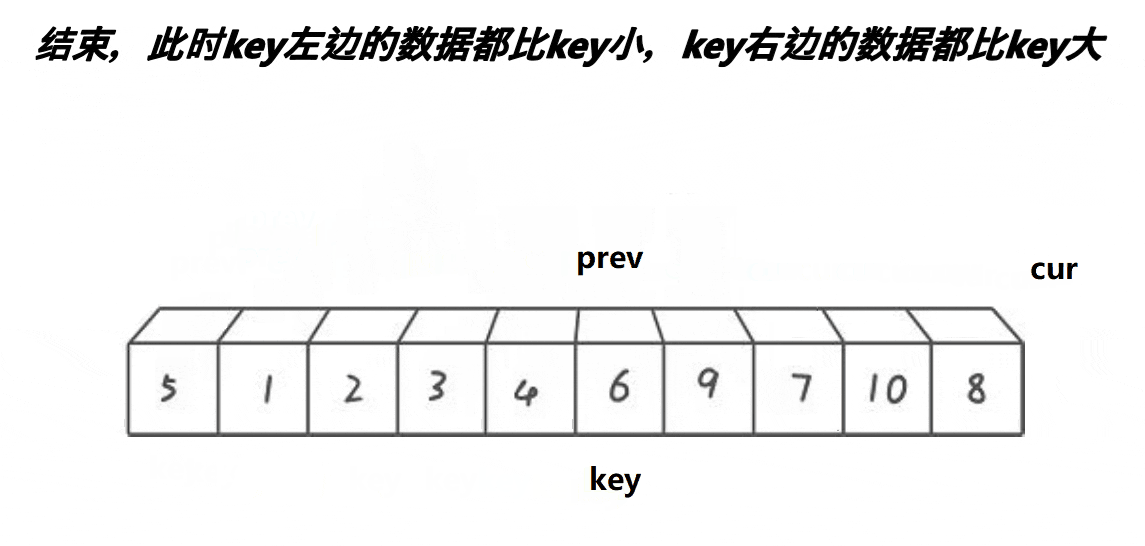
int PartSort3(int* arr, int left, int right)
{
int keyi = left;
int prev = keyi;
int cur = keyi + 1;
while (cur <= right)
{
if (arr[cur] < arr[keyi] && arr[prev++] != arr[cur])
{
Swap(&arr[cur], &arr[prev]);
}
cur++;
}
Swap(&arr[prev], &arr[keyi]);
return prev;
}
void QuickSort3(int* arr, int begin, int end)
{
if (begin >= end)
{
return;
}
int keyi = PartSort3(arr, begin, end);
QuickSort1(arr, begin, keyi - 1);
QuickSort1(arr, keyi + 1, end);
}非递归:
快排的非递归实现需要借助栈,将区间压入栈中来模拟递归
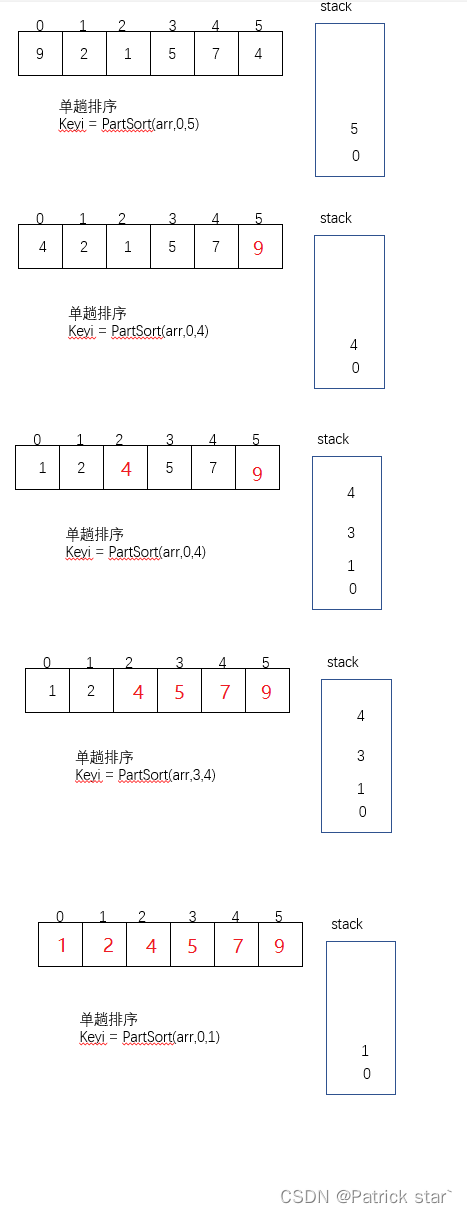
void QuickSort4(int* arr, int begin, int end)
{
int left = 0;
int right = 0;
Stack st;
StackInit(&st);
StackPush(&st, begin);
StackPush(&st, end);
while (!StackEmpty(&st))
{
right = StackTop(&st);
StackPop(&st);
left = StackTop(&st);
StackPop(&st);
int keyi = PartSort2(arr, left, right);
if (keyi-1 > left)
{
StackPush(&st, left);
StackPush(&st, keyi - 1);
}
if (right > keyi + 1)
{
StackPush(&st, keyi + 1);
StackPush(&st, right);
}
}
StackDestroy(&st);
}快排的效率取决于key的取值,如果key恰好能把待排序数组二分,则递归的层数最少,所以为了使快排的效率高,可以对key的选取进行优化,在选取key的时候可以选随机值,或者使用三数取中法(选取头尾中三个数中,值的大小在中间的那个数为key)。也可以选择在小区间是使用直接插入排序,减少递归层数。
7.归并排序
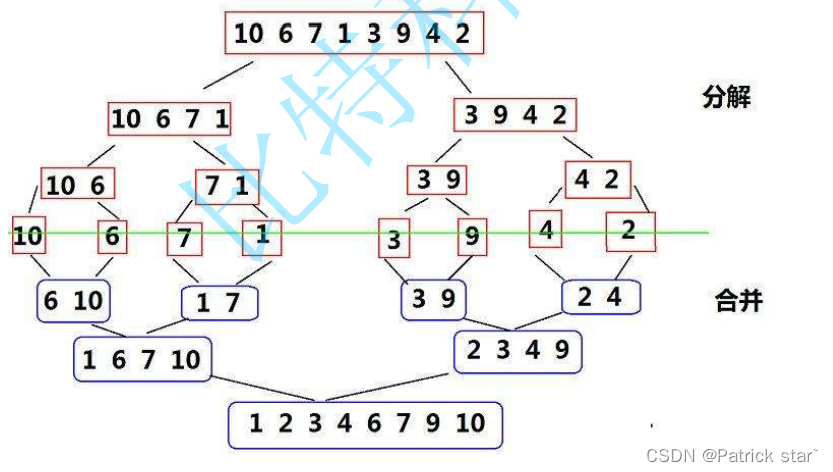
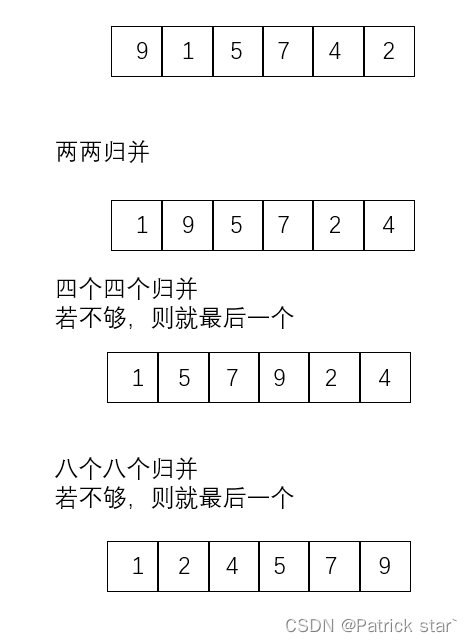
将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
void _MergeSort(int* arr,int left,int right,int* tempArray)
{
if (left >= right)
{
return;
}
int mid = (left + right) / 2;
_MergeSort(arr, left, mid,tempArray);
_MergeSort(arr, mid + 1, right,tempArray);
int begin1 = left;
int end1 = mid;
int begin2 = mid + 1;
int end2 = right;
int k = left;
while (begin1 <= end1 && begin2 <= end2 )
{
if (arr[begin1] < arr[begin2])
{
tempArray[k++] = arr[begin1++];
}
else
{
tempArray[k++] = arr[begin2++];
}
}
while (begin1 <= end1)
{
tempArray[k++] = arr[begin1++];
}
while (begin2 <= end2)
{
tempArray[k++] = arr[begin2++];
}
memmove(arr, tempArray, sizeof(int)*(right - left + 1));
}
void MergeSort(int* arr, int n)
{
int* tempArray = (int*)malloc(sizeof(int) * n);
assert(tempArray);
_MergeSort(arr, 0, n - 1, tempArray);
free(tempArray);
tempArray = NULL;
}?非递归:
?
void MergeSortNotR(int* arr, int n)
{
int* tempArray = (int*)malloc(sizeof(int) * n);
int gap = 1;
int begin1 = 0;
int begin2 = 0;
int end1 = 0;
int end2 = 0;
while (gap < n)
{
for(int i = 0;i < n;i+=2*gap)
{
begin1 = i;
end1 = begin1 + gap - 1;
begin2 = begin1 + gap;
end2 = begin2 + gap - 1;
if (end1 > n -1)
{
end1 = n - 1;
}
if (begin2 > n-1)
{
begin2 = end2 + 1;
}
else if (end2 > n - 1)
{
end2 = n - 1;
}
int k = begin1;
while (begin1 <= end1 && begin2 <= end2)
{
if (arr[begin1] < arr[begin2])
{
tempArray[k++] = arr[begin1++];
}
else
{
tempArray[k++] = arr[begin2++];
}
}
while (begin1 <= end1)
{
tempArray[k++] = arr[begin1++];
}
while (begin2 <= end2)
{
tempArray[k++] = arr[begin2++];
}
}
gap *= 2;
memmove(arr, tempArray, sizeof(int) * n);
}
free(tempArray);
}8.计数排序
计数是一个非基于比较的排序算法,它的思想是在给定的一组序列中,先找出该序列中的最大值和最小值,从而确定需要开辟多大的辅助空间,每一个数在对应的辅助空间中都有唯一的下标。
 ?
?
?
void CountSort(int* arr, int n)
{
//找到数组中的最大最小值
int max = arr[0];
int min = arr[0];
for (int i = 0; i < n; i++)
{
if (arr[i] > max)
{
max = arr[i];
}
if (arr[i] < min)
{
min = arr[i];
}
}
//给定区间
int range = max - min + 1;
int* tempArray = (int*)calloc(range,sizeof(int));//分配空间,并初始化为0
//将原数组的值映射到临时数组
for (int i = 0; i < n; i++)
{
tempArray[arr[i] - min ]++;
}
int index = 0;
for (int i = 0; i < range; i++)
{
while (tempArray[i] != 0)
{
arr[index++] = i + min;
tempArray[i]--;
}
}
}