1. 文章主要内容
? ? ? ?本篇博客主要讲解数据结构中最基本的线性查找方法,并通过线性查找法引出数据结构中类似循环不变量、时间复杂度等重要概念。此外,在构建算法之后会对其进行相关的测试。通读本篇博客大概需要10分钟左右的时间。
? ? ? ?注:本篇博客的内容是基于liuyubobobo老师讲解的数据结构课程为基础,加上本人的总结和思考制作出来的,更详细的原版视频请自行搜索bobo老师数据结构(Java版本)。
2. 线性查找法
2.1 概念
? ? ? ?不去涉入更多难以懂的概念,这里用简单的例子做一个说明。假如有一个存放整型的data数组,要在这个数组中查找值为16,如下图所示:
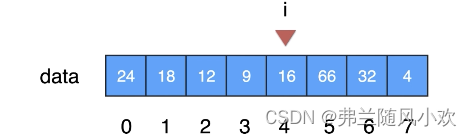
? ? ? ?线性查找法意思就是从data数组的第一个数字(索引为0的地方),往后一步步寻找16在data数组中的位置(更准确的说法应该是叫索引),如果找到了,则返回16所在data数组中的索引,如果没有找到就返回-1。(注意:这里所涉及的返回值,比如-1,是这个例子特定的,并不是线性查找法通用的返回值)这样一种线性的循环遍历方法就是叫做线性查找法。
2.2 代码实现
? ? ? ?本数据结构系列的课程都会使用Java语言来编写代码,只需要掌握Java SE部分的内容即可。首先,我们new一个LinearSearch的类来承载我们写的代码,类中有一个search方法来代表我们要编写的线性查找法,如下代码所示(注意:我们这里返回的是所查找元素的索引值,所以search方法的返回类型是整型int):
public class LinearSearch {
public static int search(int[] data, int target) {
}
}
? ? ? ?接下来构造search方法内部的逻辑实现,也就是我们线性查找方法概念说的那样,循环遍历data数组,每一个data数组内的值与需要寻找的值target进行比较。如果能够找到与target相同的值,函数就返回此时的值在data数组中的索引;如果遍历完数组,依然找不到与target相等的数值,那么函数返回值就为-1。
? ? ? ?我们使用for循环来构建整体的遍历,其中索引i的初始值为0,最大能够取到data.length - 1(注意:data.length为数组的长度,因为数组的索引最多只能取到data.length - 1)。另外,线性查找法的主体逻辑部分是在for循环中,让data数组中的每个值data[i]与target做相等的判断,如果if条件值为true,那么函数的返回此时的索引i。当整个数组循环遍历结束后,仍然找不到与target相等的值,那么此时函数的返回值为-1,代码如下所示:
public class LinearSearch {
public static int search(int[] data, int target) {
for (int i = 0; i < data.length; i++)
if (target == data[i])
return i;
return -1;
}
}
2.3 使用泛型
? ? ? ?仔细观察我们上面的代码,其传进去的参数和返回类型都是只支持整型(int),为了让search方法支持更多的数据类型,这里使用泛型来优化代码,如下代码所示:
public class LinearSearch {
public static <E> int search(E[] data, E target) {
for (int i = 0; i < data.length; i++)
if (target.equals(data[i]))
return i;
return -1;
}
}
2.4 用自定义类来测试泛型方法
? ? ? ?为了测试我们构建的泛型方法,这里首先自定义一个Student类,其中Student类中拥有成员变量name、并且覆盖equals方法(因为自定义类的equals方法,Java并没有给我们提供,所以我们需要覆盖原object方法来自定义其equals方法),而且这里equals的逻辑是将name首先转换成小写字母,然后调用字符串String的equals方法进行相等比较(注意:String类型本身重写了Object的equals方法,所以这里不需要再对String类型的equals方法进行重写了)如下代码所示:
public class Student {
private String name;
public Student(String name){
this.name = name;
}
@Override
public boolean equals(Object student){
if(this == student)
return true;
if(student == null)
return false;
if(this.getClass() != student.getClass())
return false;
Student another = (Student) student;
return this.name.toLowerCase().equals(another.name.toLowerCase());
}
}
? ? ? ?接下来在LinearSearch类中创建一个main函数进行测试,自己定义了一些数据对search方法进行验证,如下代码所示:
public class LinearSearch {
public static <E> int search(E[] data, E target) {
for (int i = 0; i < data.length; i++)
if (target.equals(data[i]))
return i;
return -1;
}
public static void main(String[] args) {
Integer[] data = {24, 18, 12, 9, 16, 66, 32, 4};
int res = LinearSearch.search(data, 16);
System.out.println(res);
int res2 = LinearSearch.search(data, 666);
System.out.println(res2);
Student[] students = {new Student("Alice"),
new Student("Bobo"),
new Student("Charles")};
Student bobo = new Student("Bobo");
int res3 = LinearSearch.search(students,bobo);
System.out.println(res3);
}
}
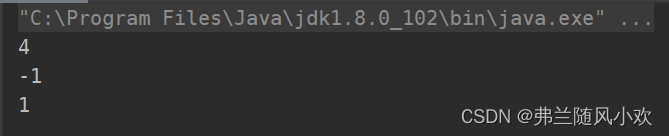
? ? ? ?其输出的结果为下图所示,表示我们所构建的search方法可以支持多种数据类型的比较:
3. 循环不变量
? ? ? ?循环不变量作为书写算法逻辑中非常重要的一环,简单的理解就是在循环当中一直保持不变的量。抓住了循环不变量,就能够很清楚的写出算法的逻辑。(之后大部分数据结构和算法都会分析其循环不变量)这里以一个简单的例子来说明,如下图所示:
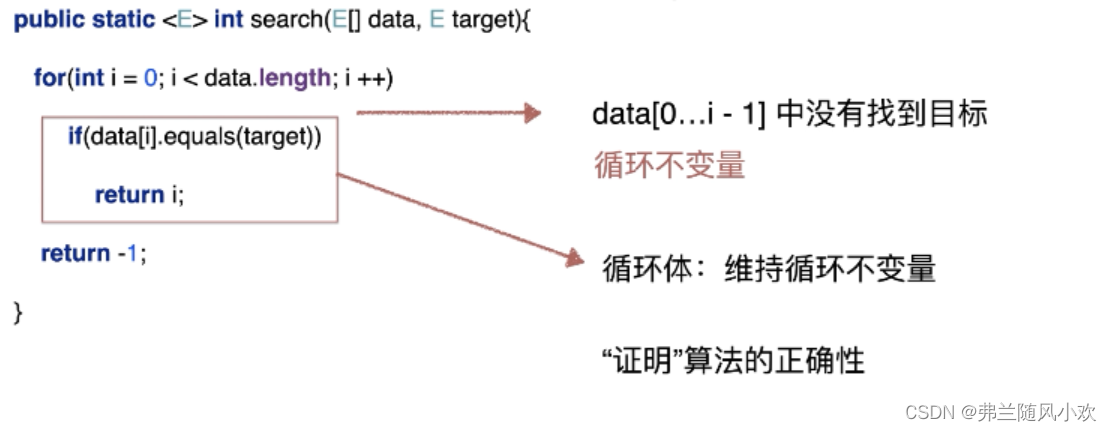
? ? ? ?这里需要注意到循环体和循环不变量,其中在整个for循环当中,data[0,i-1]中没有找到目标作为整个循环的不变量,而循环体里面的if条件一旦成立,整个循环就会结束。所以,循环体if不成立时,循环就会一直进行,此时循环不变量就会一直成立,也就是说循环体维持着循环的不变量。
4 时间复杂度分析
? ? ? ?不引入过多的书面语言,算法的时间复杂度表示算法的性能,且通常看最差的情况,一般用O表示,这里我们很清楚的知道。线性查找法对于一个长度为n的数组来说,最坏的情况是,整整扫描了一遍数组才找到或者根本没有找到目标值,这时候我们遍历了一遍数组,假设此时消耗的时间用T表示。因为我们要考虑到指令操作、赋值也会存在一些时间,所以T的一般化公式为T = C1 * n + C2(C1和C2都是常数)。
? ? ? ?又因为我们的时间复杂度描述的是随着数据规模n的增大,算法性能的变化趋势。此时应该舍弃掉常数项,所以线性查找法的时间复杂度应该为O(n)。
5 本篇小结
? ? ? ?本篇博客主要从最基础的线性查找法开始说起,涉及了循环不变量、泛型的使用、以及自定义类测试和复杂度分析的内容。文章的内容循序递进。文章有内容不对或者晦涩难懂之处,还请各位博友指出,互相学习,共同进步!