目录
目录
? ? ? 链表实质上就是链接在堆区开辟的一片数据结构。 只要明确的知道每一个节点的前驱的后继,那么链表的功能实现起来就十分容易了。
列表
? ? 列表是由具有线性逻辑次序的一组元素构成的集合:
? ? ?L={ a0 ,a1,a2. ............an-1};
? 列表是链表结构的一般推广,元素称为节点(node),分别由特定的位置链接指代。
? ? ? ?我们知道向量可以通过下标直接访问元素,此所谓“寻秩访问”(call-by-rank),而列表是通过元素的物理地址访问的,列表元素访问方式可称为“寻址访问”(call-by-position)。
节点(node)
节点是什么?
在定义节点类模板之前我们首先得知道节点是什么:
节点是内存中一片由用户分配的空间,这个节点只有物理地址,没有其他的名称供我们访问,因此我们在new一个节点的时候,用一个指针去维护他;
#define ListNodePosi(T) ListNode<T>*
ListNodePosi(T)x = new ListNode(e, this, succ);//(参数列表是拷贝构造函数)
x代表new出来的节点;
节点用来干什么?
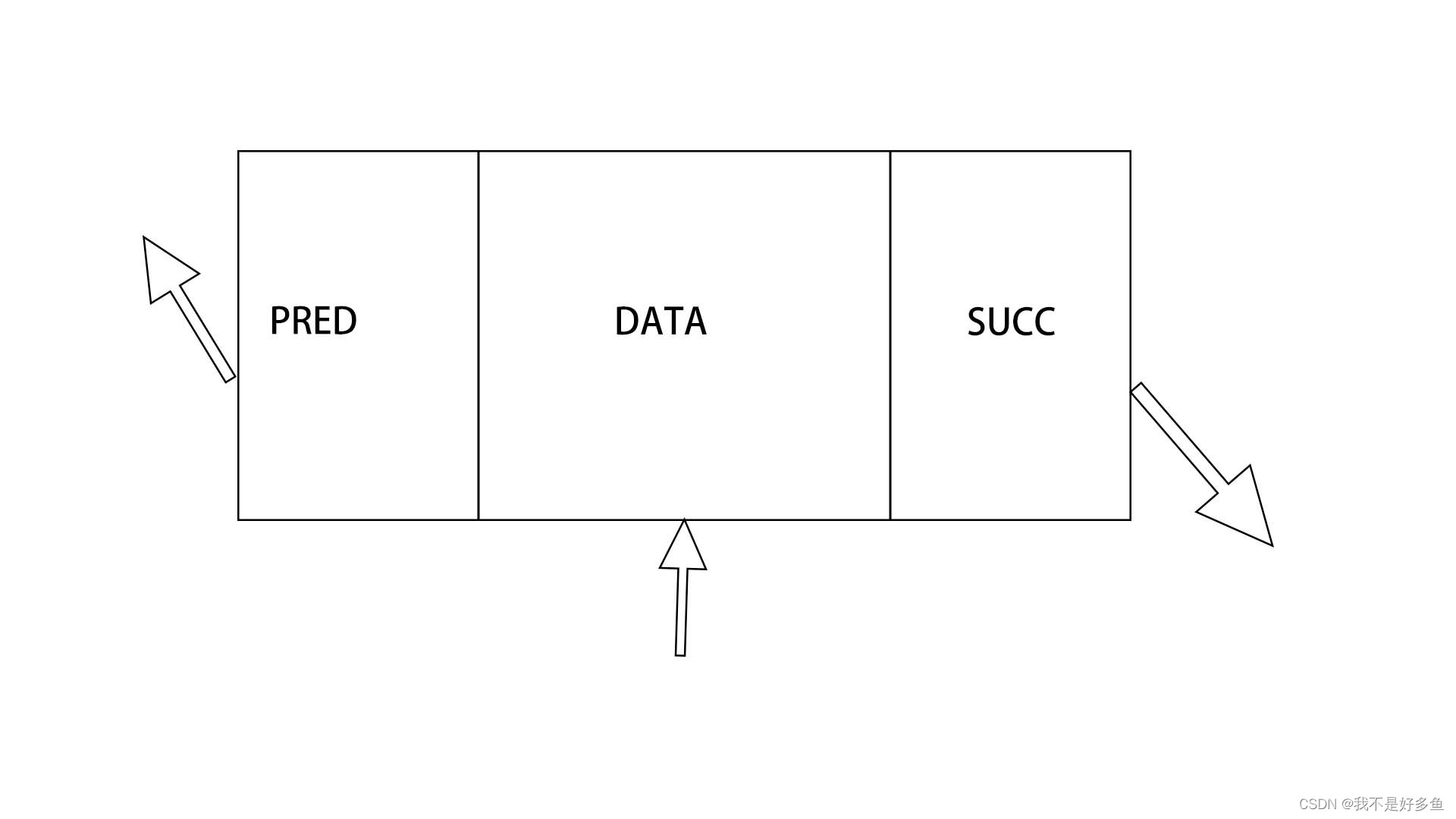
我们很清楚我们创建一个节点的目的是去存放数据的,除了存放数据,还要存放什么呢?很明显,作为一种线性的数据结构,我们还应该在节点中存放前一个节点和后一个节点的地址,这样我们就很好的将他们链接起来了。
节点类代码实现
#pragma once
typedef int Rank;//秩
#define ListNodePosi(T) ListNode<T>*
template<class T>
class ListNode
{
public:
T data;//节点所存储的数据
ListNodePosi(T) pred;//当前节点的前一个节点地址
ListNodePosi(T) succ;//当前节点的后一个节点地址
public:
ListNode();//构造函数
ListNode(T e, ListNodePosi(T)p = nullptr, ListNodePosi(T) s = nullptr);//有参构造
public:
ListNodePosi(T) insertAsPred(T const& e);//在当前节点的前面插入一个数据,并返回新节点的地址
ListNodePosi(T) insertAsSucc(T const& e);//在当前节点的后面插入一个数据,并返回新节点的地址
};
template<class T>
inline ListNode<T>::ListNode() { data = 0; pred = nullptr; succ = nullptr; }
template<class T>
inline ListNode<T>::ListNode(T e, ListNodePosi(T) p, ListNodePosi(T) s) {
this->data = e;
this->pred = p;
this->succ = s;
}
template<class T>
inline ListNodePosi(T) ListNode<T>::insertAsPred(T const& e) {
ListNodePosi(T)x = new ListNode(e, pred, this);
pred->succ = x;
pred = x;
return x;
}
template<class T>
inline ListNodePosi(T) ListNode<T>::insertAsSucc(T const& e) {
ListNodePosi(T)x = new ListNode(e, this, succ);
succ->pred = x;
succ = x;
return x;
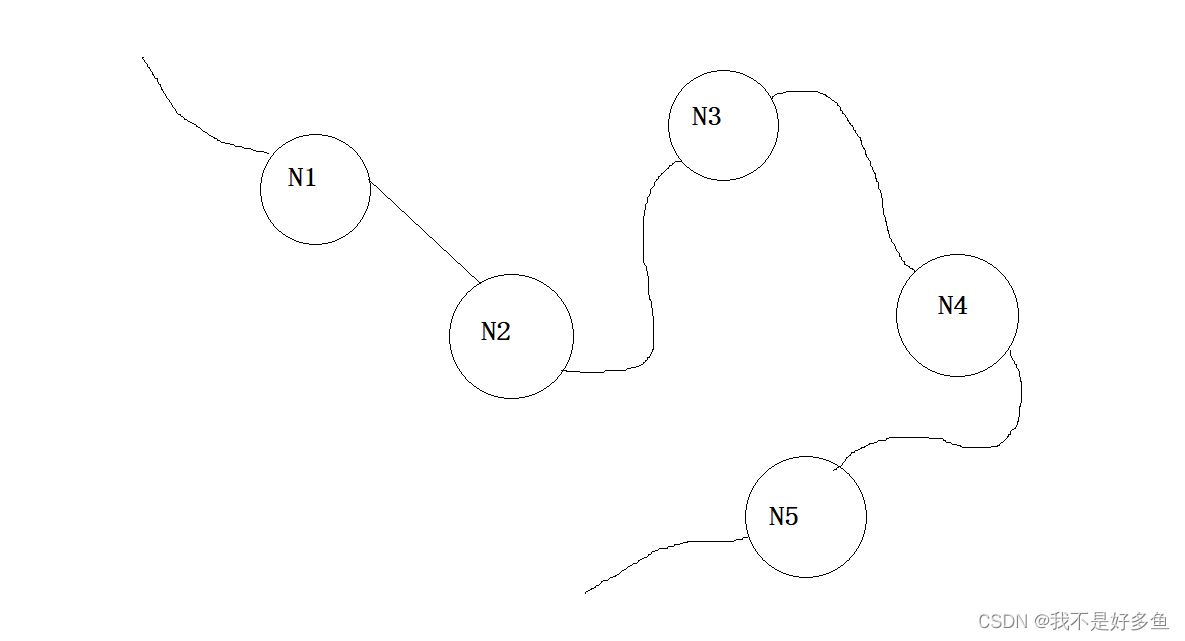
}链表:
由一系列节点按照一定的顺序连接所构成的一整条链。
图示:
创建列表的目的?
我们做一件事要有他的目的性,那我们创建列表有哪些目的呢,简单说就是列表支持的功能。
操作接口:
- size()报告列表当前规模(节点总数)
- first()? ?last()? 返回首、末节点的物理位置
- insertAsFirst(T const&e)insertAsLast(T const&e) 将e作为首末节点插入
- insert(p,e)将e作为p的后继插入
- insert(e,p)将e作为p的前驱插入
- remove(p)删除节点
- sort()排序
- find(e)查找某一元素地址
- teaverse()遍历
- deduolicate()剔除重复元素
我们对外目前提供了10个接口函数,用户可以根据具体需求去调用这些函数。
具体模板如下
template<class T>
class List
{
private:
int _size;//链表规模
ListNodePosi(T) header;//头哨兵
ListNodePosi(T) trailer;//尾哨兵
protected:
void init();//初始化函数
void copyNodes(ListNodePosi(T) p, int n);//拷贝函数
int clear();//列表清空方法
bool isMax(ListNodePosi(T)p1, ListNodePosi(T)p2);//判断节点数据大小
ListNodePosi(T) selectMax(ListNodePosi(T)p, int n);//选取数据最大的节点
ListNodePosi(T) selectMin(ListNodePosi(T)p, int n);//选取数据最小的节点
void selectSort(ListNodePosi(T)p, int n,bool choice=true);//选择排序
void _merge(ListNodePosi(T)& p, int n, List<T>& L, ListNodePosi(T)q, int m);//归并
void mergeSort(ListNodePosi(T)& p, int n);//归并排序
public:
List() { init(); }//默认构造器,即只创建一个含有头哨兵和尾哨兵的空链表
List(List<T>const& L) { copyNodes(L.first(), L._size); }//复制传入构造器的整个链表
List(List<T>const& L, int r, int n);//复制L的某一区间
~List();//列表析构器
public:
Rank size() { return this->_size; }
ListNodePosi(T) insertAsFirst(T const& e);//头节点
ListNodePosi(T) insertAsLast(T const& e);//尾节点
ListNodePosi(T) insertAfter(ListNodePosi(T) p, T const& e);//e作为p的后继插入
ListNodePosi(T) insertBefore(ListNodePosi(T)p, T const& e);//e作为p的前驱插入
ListNodePosi(T) first()const { return this->header->succ; }//返回首节点物理位置
ListNodePosi(T) last()const { return this->trailer->pred; }//返回尾节点物理位置
T remove(ListNodePosi(T)p);//删除节点
ListNodePosi(T) find(T& const e, int n, ListNodePosi(T)p)const;//查找数据所在的节点
ListNodePosi(T) find(T const& e)const;//查找数据所在的节点
int dedeuplicate();//提出列表中的重复元素;
ListNodePosi(T) search(T const& e, int n,ListNodePosi(T) p)const;//排序完成后的查找
void traverse(void(*visit)(T&));//遍历元素
void Sort(ListNodePosi(T)p, int n);//随机选取排序方法:归并、选择
int dedeuplicateProMax();
private:
T& operator[](Rank r)const;//重载下标运算符,通过秩直接访问列表节点(虽然方便,但是效率低)
};下面我们将介绍具体功能的实现
List类私有成员
private:
?? ??? ?int _size;//链表规模
?? ??? ?ListNodePosi(T) header;//头哨兵
?? ??? ?ListNodePosi(T) trailer;//尾哨兵头尾哨兵并不参与数据的存储,我们可以假象每一个链表都有一对哨兵,控制着链表的首末,这两个哨兵会大大的方便我们以后的代码实现。
构造函数与析构函数?
无参构造函数
List() { init(); }//默认构造器,即只创建一个含有头哨兵和尾哨兵的空链表template<class T>
inline void List<T>::init() {
header = new ListNode<T>;//new出来一个头哨兵节点
trailer = new ListNode<T>;//new出来一个尾哨兵节点
header->succ = trailer;//头哨兵的后继指向尾哨兵
header->pred = nullptr;//头哨兵的前驱为nullptr
trailer->pred = header;//尾哨兵的前驱为头哨兵
trailer->succ = nullptr;//尾哨兵的后继为nullptr
_size = 0;//记录链表规模为0
}new 出来两个节点交给头哨兵和尾哨兵;
让头哨兵的后继指向尾哨兵,尾哨兵的前驱指向头哨兵;
头哨兵的前驱置空,尾哨兵的后继制空
?有参构造函数
再拷贝构造之前,我们得先定义一个函数,用于复制链表的内容
template<class T> inline void List<T>::copyNodes(ListNodePosi(T) p, int n) { init();//创建头尾哨兵节点并作初始化 while (n--) { insertAsLast(p->date);//将从p起的n项以此做为尾节点插入 p = p->succ;//每次插入完成后p都指向下一个节点 } }算法:
- 创建一条链表,即含有header 和trailer的哨兵节点 调用 init()函数;
- 当需要复制的节点个数大于零时,我们不断重复插入操作?
insertAsLast(p->date);//将从p起的n项以此做为尾节点插入template<class T>//e作为尾节点插入 inline ListNodePosi(T) List<T>::insertAsLast(T const& e) { _size++; return this->trailer->insertAsPred(e); }让p指向p的后继?
复制整个链表:
List(List<T>const& L) { copyNodes(L.first(), L._size); }//复制传入构造器的整个链表
复制指定范围内的链表
template<class T>//复制L中自第r项起的n项 inline List<T>::List(List<T> const& L, int r, int n) { copyNodes(L[r], n); }?函数参数
- 复制对象? ?????????????????List<T> const& L
- 从某个节点开始? ? ? ??int r
- 复制多少个节点? ? ? ? int n
?我们发现L[r]这种形式,c++默认是不允许的,因此我们得重载运算符。
template<class T> T& List<T>::operator[](Rank r)const { ListNodePosi(T) p = this->first();//从首节点开始 while (0 < r--) { p = p->succ;//找到第r个元素 } return p->data;//返回第r个元素所存储的数据 }
析构函数
template<class T>
inline List<T>::~List() {
clear();//清空列表
delete header;//释放头哨兵
delete trailer;//释放尾哨兵
}template<class T>//清空链表 inline int List<T>::clear() { int oldSize = _size;//备份原来列表的数据量 while (0 < _size) { remove(this->header->succ);//不断删除首节点 } return oldSize;//返回删除列表节点的大小 }template<class T>//删除节点p inline T List<T>::remove(ListNodePosi(T) p) { T e = p->data;//备份p所指向的数据 p->pred->succ = p->succ;//p的前驱的后继为p的后继 p->succ->pred = p->pred;//p后继的前驱为p的前驱 delete p;//释放p内存 this->_size--;//链表规模-- return e;//返回p节点的数据 }算法实现:
- 备份该节点所储存的信息;
- 更新该节点的前驱的后继为该节点的后继;
- 更新该节点后继的前驱为该节点的前驱;
- 释放该节点;
- 存储规模减一
- 返回该节点的数据
删除前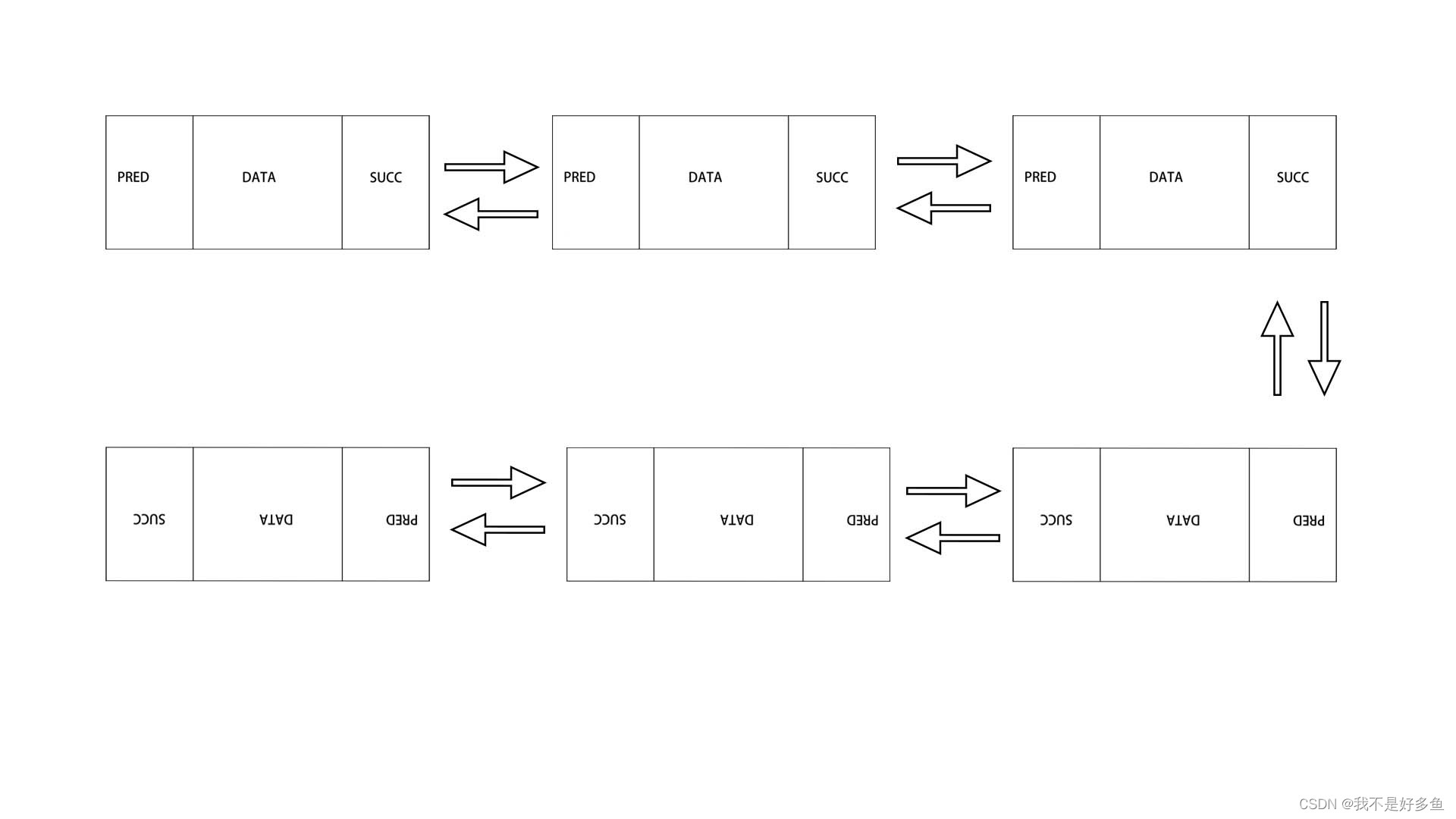 ?
?
删除后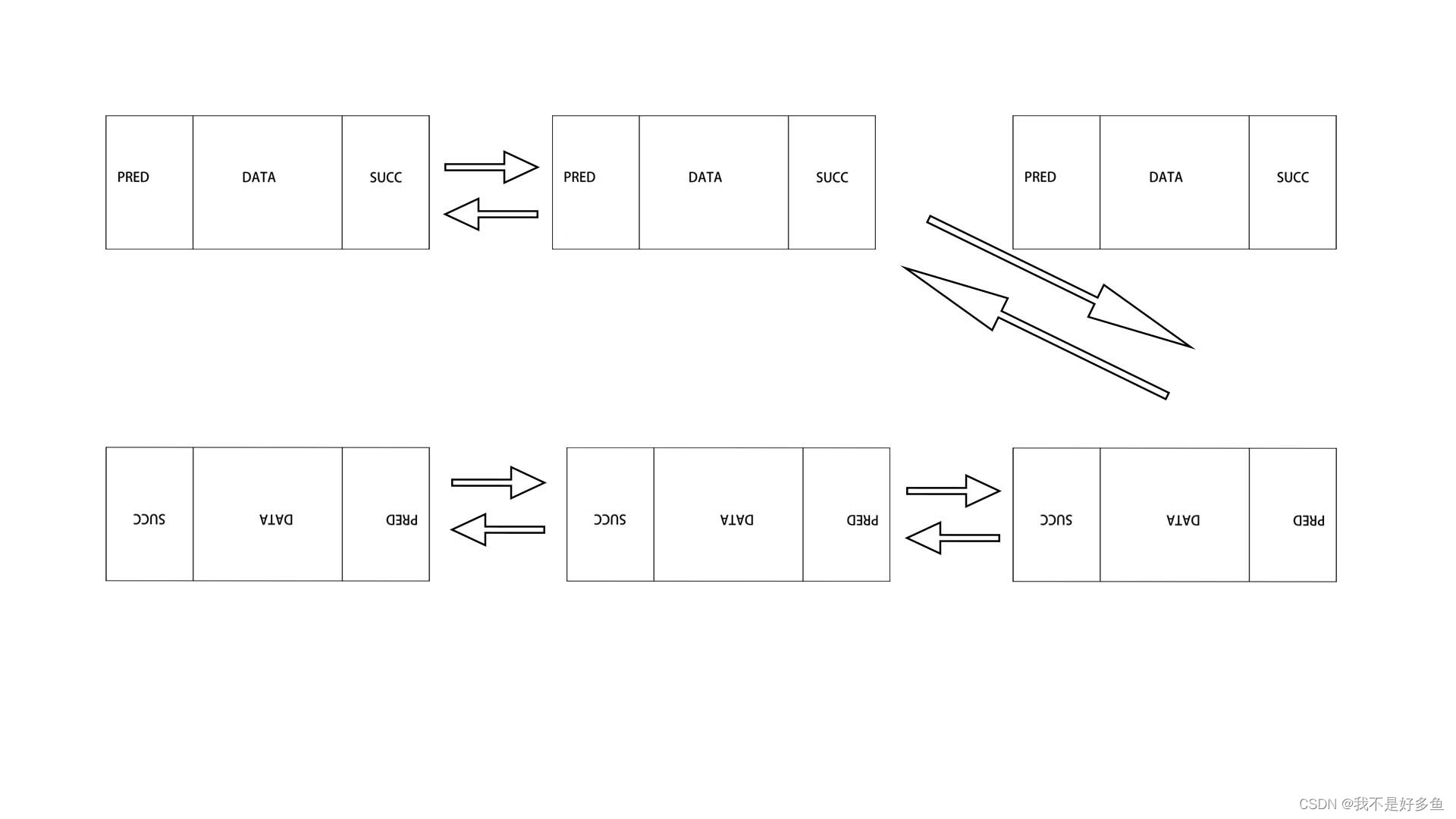 ?
?
?对外接口
size()
这个函数实现非常容易
int size() { return this->_size; }
??返回首、末节点的物理位置
?????利用哨兵节点的便利直接返回
ListNodePosi(T) first()const { return this->header->succ; }//返回首节点物理位置 ListNodePosi(T) last()const { return this->trailer->pred; }//返回尾节点物理位置
?将e作为首末节点插入?
template<class T>//e作为首节点插入
inline ListNodePosi(T) List<T>::insertAsFirst(T const& e) {
_size++;//规模++
return header->insertAsSucc(e);//返回前插节点的物理位置
}
template<class T>//e作为尾节点插入
inline ListNodePosi(T) List<T>::insertAsLast(T const& e) {
_size++;
return this->trailer->insertAsPred(e);
}?将e作为p的后继插入
template<class T>//e作为尾节点插入
inline ListNodePosi(T) List<T>::insertAsLast(T const& e) {
_size++;
return this->trailer->insertAsPred(e);
}
?将e作为p的后继插入
template<class T>//e作为p的后继插入
inline ListNodePosi(T) List<T>::insertAfter(ListNodePosi(T) p, T const& e) {
this->_size++;
return p->insertAsSucc(e);
}
remove(p)删除节点
template<class T>//删除节点p
inline T List<T>::remove(ListNodePosi(T) p) {
T e = p->data;//备份p所指向的数据
p->pred->succ = p->succ;//p的前驱的后继为p的后继
p->succ->pred = p->pred;//p后继的前驱为p的前驱
delete p;//释放p内存
this->_size--;//链表规模--
return e;//返回p节点的数据
}算法实现:
- 备份该节点所储存的信息;
- 更新该节点的前驱的后继为该节点的后继;
- 更新该节点后继的前驱为该节点的前驱;
- 释放该节点;
- 存储规模减一
- 返回该节点的数据
?sort()排序
template<class T> inline void List<T>::Sort(ListNodePosi(T) p, int n) { switch (rand() % 2) { case 0:selectSort(p, n); break; case 1:mergeSort(p, n); break; } }随机从selectSort和mergerSort两种排序算法中选取一种算法,下面我们来介绍这两种算法
selectSort(ListNodePosi(T) p, int n)
选择排序,顾名思义,先选择出链表中最大或者最小的元素,然后按照由大到小或者由小到大的顺序排列。因此我们考虑封装一个选择最大元素和最小元素的函数。
template<class T>//查询列表中最大数据 inline ListNodePosi(T) List<T>::selectMax(ListNodePosi(T) p, int n) { ListNodePosi(T)max = p;//将其实最大值设为p for (ListNodePosi(T) cur = p; 1 < n; n--) { //从节点p开始往后查询n个节点 if (isMax(cur = cur->succ, max)) { //isMax这个函数,第一个参数表比第二个参数所存储的数据大返回true max = cur;//将cur节点给max; } } return max; } template<class T>//查询列表中最小数据 inline ListNodePosi(T) List<T>::selectMin(ListNodePosi(T) p, int n) { ListNodePosi(T)min = p; for (ListNodePosi(T) cur = p; 1 < n; n--) { if (!isMax(cur = cur->succ, min)) { min = cur; } } return min; } template<class T>//比较两个节点所存数据的大小 inline bool List<T>::isMax(ListNodePosi(T) p1, ListNodePosi(T) p2) { if (p1->data >= p2->data)return true; else return false; }? ? ? ? 算法:查找最大元素
- ?从首节点开始,先将最大值设为p
- 从该节点开始往后遍历n次,调用比较函数inline bool List<T>::isMax(ListNodePosi(T) p1, ListNodePosi(T) p2)
- 如果后面的数据比前面的大,将该值赋予max
- 返回max
? 算法:查找最小元素
- ?从首节点开始,先将最小值设为p
- 从该节点开始往后遍历n次,调用比较函数inline bool List<T>::isMax(ListNodePosi(T) p1, ListNodePosi(T) p2)
- 如果后面的数据比前面的小,将该值赋予min
- 返回min
?主排序函数:
void selectSort(ListNodePosi(T)p, int n,bool choice=true); template<class T> inline void List<T>::selectSort(ListNodePosi(T) p, int n,bool choice) { ListNodePosi(T)head = p->pred; ListNodePosi(T)tail = p; for (int i = 0; i < n; i++) { tail = tail->succ; } while (1 < n) { if (choice) { ListNodePosi(T) max = selectMax(head->succ, n); insertBefore(tail, remove(max)); } else { ListNodePosi(T) min = selectMin(head->succ, n); insertBefore(tail, remove(min)); } tail = tail->pred; n--; } }该函数默认排序方法是小到大,我们还提供了一种从大到小的方式,只需要用户输入false即可由大到小;
传入参数(从某个节点开始排列,具体排多少个节点)
算法实现:
- 创建一个head指针指向p的后继,tail指针指向p
- 让tail指向tail的后继重复n次来到末端
- 选取最大节点,将最大节点插入在tail的前驱
- n--;tail移动到自己的前驱
- 重复2,3步骤,直到n>z;
归并排序法
?
template<class T> inline void List<T>::mergeSort(ListNodePosi(T)& p, int n) { if (n < 2)return; int m = n >> 1; ListNodePosi(T)q = p; for (int i = 0; i < m; i++)q = q->succ; mergeSort(p, m); mergeSort(q, n - m); _merge(p, m, *this, q, n - m); }template<class T> inline void List<T>::_merge(ListNodePosi(T)& p, int n, List<T>& L, ListNodePosi(T) q, int m) { ListNodePosi(T)pp = p->pred; while ((0 <m) && (q != p)) //q尚未出界(或在mergeSort()中,p亦尚未出界)之前 if ((0 < n) && (p->data <= q->data)) //若p尚未出界且v(p) <= v(q),则 { p = p->succ; n--; } //p直接后移,即完成归入 else //否则,将q转移至p之前,以完成归入 { insertBefore(p,L.remove((q = q->succ)->pred)); m--; } p= pp->succ; //更新的首节点 }算法:
- 将一条链表按照中间拆成两部分
- 对左边的链表在进行拆解,对右边的链表在进行拆解,知道链表长度小于2
- 调用归并函数,对左右两链表间进行排列,整合成一个大链表
- 重复操作,直到排好序。?
?归并算法:
- 创建一个新指针指向左链表的前驱;
- 当左右链表均为出界时
- p未出界同时p节点存储的数据小于或者等于q节点存储的数据时p节点后移,n--
- 其他情况即p出界或者p数据大于q数据则将q数据作为p的前驱插入,q右移,并且删除q节点,右链表长度--
- 更新首节点,排好序的链表就完成了;
?
查找某一元素
template<class T> inline ListNodePosi(T) List<T>::find(T& const e, int n, ListNodePosi(T) p) const { while (0 < n--) { if (e == (p=p->pred)->data)return p; } return nullptr; }?
从后往前遍历列表,查找到了返回该元素物理地址;?
遍历
template<class T>
inline void List<T>::traverse(void(*visit)(T&)) {
for (ListNodePosi(T)p = first(); p != this->trailer; p = p->succ) {
visit(p->data);
}
}
template<class T>
void show(T e) {
std::cout << e << ' ';
}
//遍历元素剔除重复元素
template<class T> inline int List<T>::dedeuplicate() { if (this->_size < 2)return 0;//平凡列表自然无重复元素,不需要剔除 int oldSize = this->_size;//记录原始规模大小 ListNodePosi(T) p = this->header; Rank r = 0; while (trailer!=(p = p->succ)) { ListNodePosi(T) q = find(p->data, r, p); q ? remove(q) : r++; } return oldSize - _size; }剔除
算法实现:
- 记录原始链表规模
- 将头节点的物理地址赋给一个新节点
- 当新节点的物理位置不等于尾哨兵时,不断执行:在r p的范围查找p指针所指的数据,如果有相同的,那么删除这个元素 r++
- 返回现有规模;
template<class T> inline int List<T>::dedeuplicateProMax() { if (this->_size < 2)return 0;//平凡列表自然无重复元素,不需要剔除 int oldSize = this->_size;//记录原始规模大小 ListNodePosi(T) p = first(); ListNodePosi(T) q; while (trailer != (q = p->succ)) if (p->data != q->data)p = q; else remove(q); return oldSize - _size; }?有序列表剔除
算法图解:
算法:
- 创建两个节点 p=first(),q
- q=p->succ;当q补位尾哨兵时不断执行 如果p q数据不相等 p=q;相等剔除q
- p q 后移动
- 返回当前规模,?
完整代码如下
?
#pragma once typedef int Rank;//秩 #define ListNodePosi(T) ListNode<T>* template<class T> class ListNode { //friend class List; public: T data; ListNodePosi(T) pred; ListNodePosi(T) succ; public: ListNode() { data= 0; pred = nullptr; succ = nullptr; }; ListNode(T e, ListNodePosi(T)p = nullptr, ListNodePosi(T) s = nullptr); public: ListNodePosi(T) insertAsPred(T const& e); ListNodePosi(T) insertAsSucc(T const& e); }; template<class T> inline ListNode<T>::ListNode(T e, ListNodePosi(T) p, ListNodePosi(T) s) { this->data = e; this->pred = p; this->succ = s; } template<class T> inline ListNodePosi(T) ListNode<T>::insertAsPred(T const& e) { ListNodePosi(T)x = new ListNode(e, pred, this); pred->succ = x; pred = x; return x; } template<class T> inline ListNodePosi(T) ListNode<T>::insertAsSucc(T const& e) { ListNodePosi(T)x = new ListNode(e, this, succ); succ->pred = x; succ = x; return x; }#pragma once #include"ListNode.hpp" #include<iostream> namespace myList { template<class T> class List { private: int _size;//链表规模 ListNodePosi(T) header;//头哨兵 ListNodePosi(T) trailer;//尾哨兵 protected: void init();//初始化函数 void copyNodes(ListNodePosi(T) p, int n);//拷贝函数 int clear();//列表清空方法 bool isMax(ListNodePosi(T)p1, ListNodePosi(T)p2);//判断节点数据大小 ListNodePosi(T) selectMax(ListNodePosi(T)p, int n);//选取数据最大的节点 ListNodePosi(T) selectMin(ListNodePosi(T)p, int n);//选取数据最小的节点 void selectSort(ListNodePosi(T)p, int n,bool choice=true);//选择排序 void _merge(ListNodePosi(T)& p, int n, List<T>& L, ListNodePosi(T)q, int m);//归并 void mergeSort(ListNodePosi(T)& p, int n);//归并排序 public: List() { init(); }//默认构造器,即只创建一个含有头哨兵和尾哨兵的空链表 List(List<T>const& L) { copyNodes(L.first(), L._size); }//复制传入构造器的整个链表 List(List<T>const& L, int r, int n);//复制L的某一区间 ~List();//列表析构器 public: Rank size() { return this->_size; } ListNodePosi(T) insertAsFirst(T const& e);//头节点 ListNodePosi(T) insertAsLast(T const& e);//尾节点 ListNodePosi(T) insertAfter(ListNodePosi(T) p, T const& e);//e作为p的后继插入 ListNodePosi(T) insertBefore(ListNodePosi(T)p, T const& e);//e作为p的前驱插入 ListNodePosi(T) first()const { return this->header->succ; }//返回首节点物理位置 ListNodePosi(T) last()const { return this->trailer->pred; }//返回尾节点物理位置 T remove(ListNodePosi(T)p);//删除节点 ListNodePosi(T) find(T& const e, int n, ListNodePosi(T)p)const;//查找数据所在的节点 ListNodePosi(T) find(T const& e)const;//查找数据所在的节点 int dedeuplicate();//提出列表中的重复元素; ListNodePosi(T) search(T const& e, int n,ListNodePosi(T) p)const;//排序完成后的查找 void traverse(void(*visit)(T&));//遍历元素 void Sort(ListNodePosi(T)p, int n);//随机选取排序方法:归并、选择 int dedeuplicateProMax(); private: T& operator[](Rank r)const;//重载下标运算符,通过秩直接访问列表节点(虽然方便,但是效率低) }; template<class T> inline void List<T>::init() { header = new ListNode<T>;//new出来一个头哨兵节点 trailer = new ListNode<T>;//new出来一个尾哨兵节点 header->succ = trailer;//头哨兵的后继指向尾哨兵 header->pred = nullptr;//头哨兵的前驱为nullptr trailer->pred = header;//尾哨兵的前驱为头哨兵 trailer->succ = nullptr;//尾哨兵的后继为nullptr _size = 0;//记录链表规模为0 } template<class T>//复制传入构造器的整个链表 inline void List<T>::copyNodes(ListNodePosi(T) p, int n) { init();//创建头尾哨兵节点并作初始化 while (n--) { insertAsLast(p->date);//将从p起的n项以此做为尾节点插入 p = p->succ;//每次插入完成后p都指向下一个节点 } } template<class T>//清空链表 inline int List<T>::clear() { int oldSize = _size;//备份原来列表的数据量 while (0 < _size) { remove(this->header->succ);//不断删除首节点 } return oldSize;//返回删除列表节点的大小 } //列表清空方法 template<class T>//比较两个节点所存数据的大小 inline bool List<T>::isMax(ListNodePosi(T) p1, ListNodePosi(T) p2) { if (p1->data >= p2->data)return true; else return false; } template<class T>//查询列表中最大数据 inline ListNodePosi(T) List<T>::selectMax(ListNodePosi(T) p, int n) { ListNodePosi(T)max = p;//将其实最大值设为p for (ListNodePosi(T) cur = p; 1 < n; n--) { //从节点p开始往后查询n个节点 if (isMax(cur = cur->succ, max)) { //isMax这个函数,第一个参数表比第二个参数所存储的数据大返回true max = cur;//将cur节点给max; } } return max; } template<class T>//查询列表中最小数据 inline ListNodePosi(T) List<T>::selectMin(ListNodePosi(T) p, int n) { ListNodePosi(T)min = p; for (ListNodePosi(T) cur = p; 1 < n; n--) { if (!isMax(cur = cur->succ, min)) { min = cur; } } return min; } template<class T> inline void List<T>::selectSort(ListNodePosi(T) p, int n,bool choice) { ListNodePosi(T)head = p->pred; ListNodePosi(T)tail = p; for (int i = 0; i < n; i++) { tail = tail->succ; } while (1 < n) { if (choice) { ListNodePosi(T) max = selectMax(head->succ, n); insertBefore(tail, remove(max)); } else { ListNodePosi(T) min = selectMin(head->succ, n); insertBefore(tail, remove(min)); } tail = tail->pred; n--; } } template<class T> inline void List<T>::_merge(ListNodePosi(T)& p, int n, List<T>& L, ListNodePosi(T) q, int m) { ListNodePosi(T)pp = p->pred; while ((0 <m) && (q != p)) //q尚未出界(或在mergeSort()中,p亦尚未出界)之前 if ((0 < n) && (p->data <= q->data)) //若p尚未出界且v(p) <= v(q),则 { p = p->succ; n--; } //p直接后移,即完成归入 else //否则,将q转移至p之前,以完成归入 { insertBefore(p,L.remove((q = q->succ)->pred)); m--; } p= pp->succ; //更新的首节点 } template<class T> inline void List<T>::mergeSort(ListNodePosi(T)& p, int n) { if (n < 2)return; int m = n >> 1; ListNodePosi(T)q = p; for (int i = 0; i < m; i++)q = q->succ; mergeSort(p, m); mergeSort(q, n - m); _merge(p, m, *this, q, n - m); } template<class T>//复制L中自第r项起的n项 inline List<T>::List(List<T> const& L, int r, int n) { copyNodes(L[r], n); } template<class T> inline List<T>::~List() { clear();//清空列表 delete header;//释放头哨兵 delete trailer;//释放尾哨兵 } template<class T>//e作为首节点插入 inline ListNodePosi(T) List<T>::insertAsFirst(T const& e) { _size++;//规模++ return header->insertAsSucc(e);//返回前插节点的物理位置 } template<class T>//e作为尾节点插入 inline ListNodePosi(T) List<T>::insertAsLast(T const& e) { _size++; return this->trailer->insertAsPred(e); } template<class T>//e作为p的后继插入 inline ListNodePosi(T) List<T>::insertAfter(ListNodePosi(T) p, T const& e) { this->_size++; return p->insertAsSucc(e); } template<class T>//e作为p的前驱插入 inline ListNodePosi(T) List<T>::insertBefore(ListNodePosi(T) p, T const& e) { this->_size++; return p->insertAsPred(e); } template<class T>//删除节点p inline T List<T>::remove(ListNodePosi(T) p) { T e = p->data;//备份p所指向的数据 p->pred->succ = p->succ;//p的前驱的后继为p的后继 p->succ->pred = p->pred;//p后继的前驱为p的前驱 delete p;//释放p内存 this->_size--;//链表规模-- return e;//返回p节点的数据 } template<class T> inline ListNodePosi(T) List<T>::find(T& const e, int n, ListNodePosi(T) p) const { while (0 < n--) { if (e == (p=p->pred)->data)return p; } return nullptr; } template<class T> inline ListNodePosi(T) List<T>::find(T const& e) const { return find(e, _size, trailer); } template<class T> inline int List<T>::dedeuplicate() { if (this->_size < 2)return 0;//平凡列表自然无重复元素,不需要剔除 int oldSize = this->_size;//记录原始规模大小 ListNodePosi(T) p = this->header; Rank r = 0; while (trailer!=(p = p->succ)) { ListNodePosi(T) q = find(p->data, r, p); q ? remove(q) : r++; } return oldSize - _size; } template<class T> inline ListNodePosi(T) List<T>::search(T const& e,int n, ListNodePosi(T) p) const { while (0 <= n--) { if (p->pred->data == e)break; p = p->pred; } return p; } template<class T> inline void List<T>::traverse(void(*visit)(T&)) { for (ListNodePosi(T)p = first(); p != this->trailer; p = p->succ) { visit(p->data); } } //遍历元素 template<class T> inline void List<T>::Sort(ListNodePosi(T) p, int n) { switch (rand() % 2) { case 0:selectSort(p, n); break; case 1:mergeSort(p, n); break; } } //随机选取排序方法:归并、选择 template<class T> inline int List<T>::dedeuplicateProMax() { if (this->_size < 2)return 0;//平凡列表自然无重复元素,不需要剔除 int oldSize = this->_size;//记录原始规模大小 ListNodePosi(T) p = first(); ListNodePosi(T) q; while (trailer != (q = p->succ)) if (p->data != q->data)p = q; else remove(q); return oldSize - _size; } template<class T> void show(T e) { std::cout << e << ' '; } template<class T> T& List<T>::operator[](Rank r)const { ListNodePosi(T) p = this->first();//从首节点开始 while (0 < r--) { p = p->succ;//找到第r个元素 } return p->data;//返回第r个元素所存储的数据 } }
总结
? ? ? 链表实质上就是链接在堆区开辟的一片数据结构。 只要明确的知道每一个节点的前驱的后继,那么链表的功能实现起来就十分容易了。