系列文章目录
刷题笔记(一)–数组类型:二分法
刷题笔记(二)–数组类型:双指针法
刷题笔记(三)–数组类型:滑动窗口
刷题笔记(四)–数组类型:模拟
刷题笔记(五)–链表类型:基础题目以及操作
刷题笔记(六)–哈希表:基础题目和思想
刷题笔记(七)–字符串:经典题目
刷题笔记(八)–双指针:两数之和以及延伸
刷题笔记(九)–字符串:KMP算法
刷题笔记(十)–栈和队列:基础题目
刷题笔记(十一)–栈和队列:Top-K问题
刷题笔记(十二)–复习:排序算法
刷题笔记(十三)–二叉树:前中后序遍历(复习)
刷题笔记(十四)–二叉树:层序遍历和DFS,BFS
刷题笔记(十五)–二叉树:属性相关题目
刷题笔记(十六)–二叉树:修改与构造
刷题笔记(十七)–二叉搜索树:关于属性问题
刷题笔记(十八)–二叉树:公共祖先问题
刷题笔记(十九)–二叉树:二叉搜索树的修改与构造
刷题笔记(二十)–回溯算法:组合问题
刷题笔记(二十一)–回溯算法:分割丶子集丶全排列问题
前言
想了想,还是继续往下走,但是习题的内容的话要变一变,里面要有各大热门习题,中间跳了贪心算法,直接往下走。
这一篇博客主要就是讲一下关于动态规划的基础思想,以及做题的模板。
模板
什么是动态规划呢?
所谓动态规划是分治思想的延续,通俗一点来说就是大事化小,小事化了的艺术。在不断的将问题化为最小问题的分治过程中,保存对这些小问题已经处理好的结果,并且供后面使用。
动态规划有以下三个特点:
1.把原来的问题分解成了几个相似的子问题
2.所有的子问题都只需要解决一次
3.储存子问题的解
所以动态规划问题的本质,就是对问题状态的定义和状态转移方程的定义(状态和状态之间的递归关系)。
我们一般从以下四个角度考虑
1.状态定义
2.状态间的转移方程定义
3.状态的初始化
4.返回结果
状态定义的要求:定义的状态一定要形成递推关系。所以一句话概括:三特点四要素两本质
一般使用如下场景
最大值/最小值,可不可行,是不是,方案个数
题录
746. 使用最小花费爬楼梯
题目链接如下:
题目截图如下:
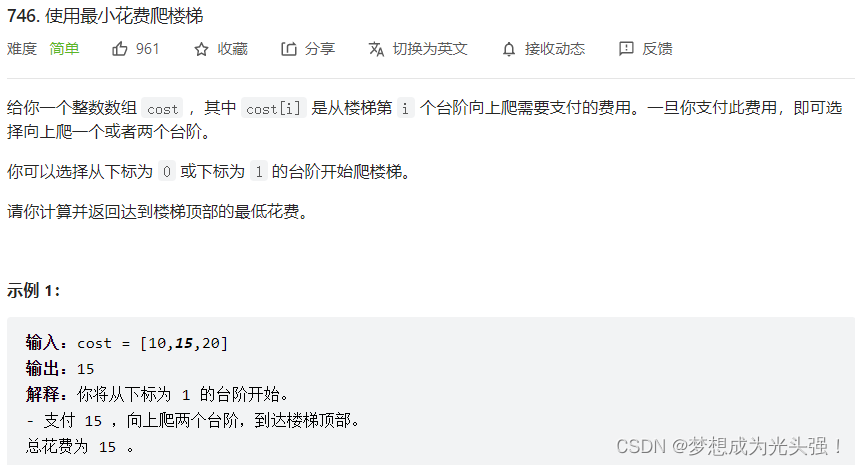
首先,这道题就是根据我们的状态转移方程来进行解决。
我们创建一个dp[]数组,用来存放我们到达i位置时刻的最小花费,所以我们的状态转移方程就出来了
dp[i] = Math.min(dp[i - 1] + cost[i - 1],dp[i - 2] + cost[i - 2]);
还有就是你要明白,dp[]数字的初始定义,一定是从2下标开始
所以题解如下:
public class 最小花费爬楼梯 {
public int minCostClimbingStairs(int[] cost) {
int[] dp = new int[cost.length + 1];
dp[0] = 0;
dp[1] = 0;
for (int i = 2; i <= cost.length; i++) {
dp[i] = Math.min(dp[i - 1] + cost[i - 1],dp[i - 2] + cost[i - 2]);
}
return dp[cost.length];
}
}
62. 不同路径
题目链接如下:
题目截图如下:

这个题目的状态转移方程很容易就能看出来,因为机器人只能往下或者往右走,所以到达当前方格的路径条数就等于到达上方 + 右方的条数,也就是
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
但是这里要注意一下,就是当i == 0或者 j == 0的时候,路径永远只有一条
public class 不同路径 {
public int uniquePaths(int m, int n) {
int[][] dp = new int[m][n];
dp[0][0] = 1;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if(i == 0 || j == 0) {
dp[i][j] = 1;
}else{
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
}
return dp[m - 1][n - 1];
}
}
63. 不同路径 II
题目链接如下:
题目截图如下:

这个题目是不是就很诡异了?但是其实还是和上面一样的思路,怎么说呢?
因为你状态转移方程是没有变得呀,还是
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
但是这里是有一个问题的,就是你要加一个判断,当前位置在原数组中不是阻碍,也就是值不为1。
这里的问题处理完之后呢,还有就是比较特殊的边界处理,就是那个石头在第一行或者第一列的时候,所以总体代码如下:
public class 不同路径_2 {
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
int m = obstacleGrid.length;
int n = obstacleGrid[0].length;
int[][] dp = new int[m][n];
for (int i = 0; i < n && obstacleGrid[0][i] == 0; i++) {
dp[0][i] = 1;
}
for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) {
dp[i][0] = 1;
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
if(obstacleGrid[i][j] == 0){
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
}
return dp[m - 1][n - 1];
}
}
53. 最大子数组和
题目链接如下:
题目截图如下:
这个题目,还是比较亲切的,怎么说呢,最大子数组和,你怎么知道当前位置的最大子数组和是多少呢?
那就是前一个位置的数组最大和加上当前值后和当前数组最大和的比较,如下,我们题目中的数组名称是nums
dp[i] = Math.max(dp[i - 1] + nums[i],nums[i]);
所以题目解法如下:
public class 最大子数组的和 {
public int maxSubArray(int[] nums) {
if(nums.length == 0 || nums == null) return 0;
int[] dp = new int[nums.length];
dp[0] = nums[0];
int max = nums[0];
for (int i = 1; i < nums.length; i++) {
dp[i] = Math.max(dp[i - 1] + nums[i],nums[i]);
if(dp[i] > max){
max = dp[i];
}
}
return max;
}
}
343. 整数拆分
题目链接如下:
题目截图如下:
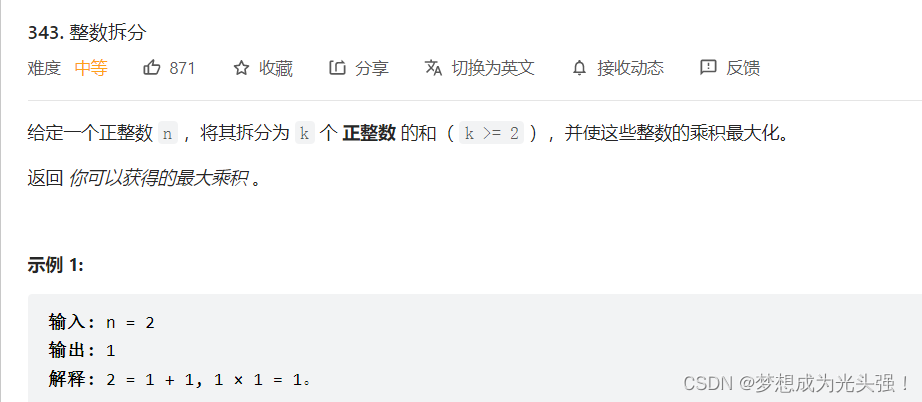
这个题目我们主要是想清楚,状态转移方程到底怎么写。首先,n >= 2的时候,整数可以怎么拆分?比如说,我们[1,n]这个区间,我们随便先取一个数k,那么这个问题是不是就可以分解成是[(n - k) * k]大,还是k * (n - k )的最大拆分后的乘积数最大?是不是有点绕,那就继续
创建数组 dp,其中dp[i] 表示将正整数 i拆分成至少两个正整数的和之后,这些正整数的最大乘积。特别地,0不是正整数,1是最小的正整数,0 和 1 都不能拆分,因此dp[0]=dp[1]=0。继续往下走:
当i≥2 时,假设对正整数 i 拆分出的第一个正整数是 j,则有以下两种方案:
将 i 拆分成 j 和 i?j 的和,且i?j 不再拆分成多个正整数,此时的乘积是j×(i?j);
将 i 拆分成 j 和 i?j 的和,且i?j 继续拆分成多个正整数,此时的乘积是j×dp[i?j]。
这样说的话能理解了吗?
所以从单个数字来讲,也就是一个j的情况下,当前的状态转移方程就应该是
dp[i]=Math.max(j×(i?j),j×dp[i?j])
但是j不止一个呀,也就比如说dp[15],那么在这之前,我可以把作为第一个拆分数,我也可以把10作为第一个拆分数不是?那么这个时候我们就要遍历了,遍历的途中记录最大的那个拆分树
int max = 0;
for (int j = 1; j < i; j++) {
max = Math.max(max,Math.max(j * (i - j),j * dp[j - i]));
}
所以总体代码如下:
public class 整数拆分 {
public int integerBreak(int n) {
int[] dp = new int[n + 1];
dp[0] = dp[1] = 0;
for (int i = 2; i < n; i++) {
int max = 0;
for (int j = 1; j < i; j++) {
max = Math.max(max,Math.max(j * (i - j),j * dp[j - i]));
}
dp[i] = max;
}
return dp[n];
}
}
96.不同的二叉搜索树
题目链接如下:
题目截图如下:
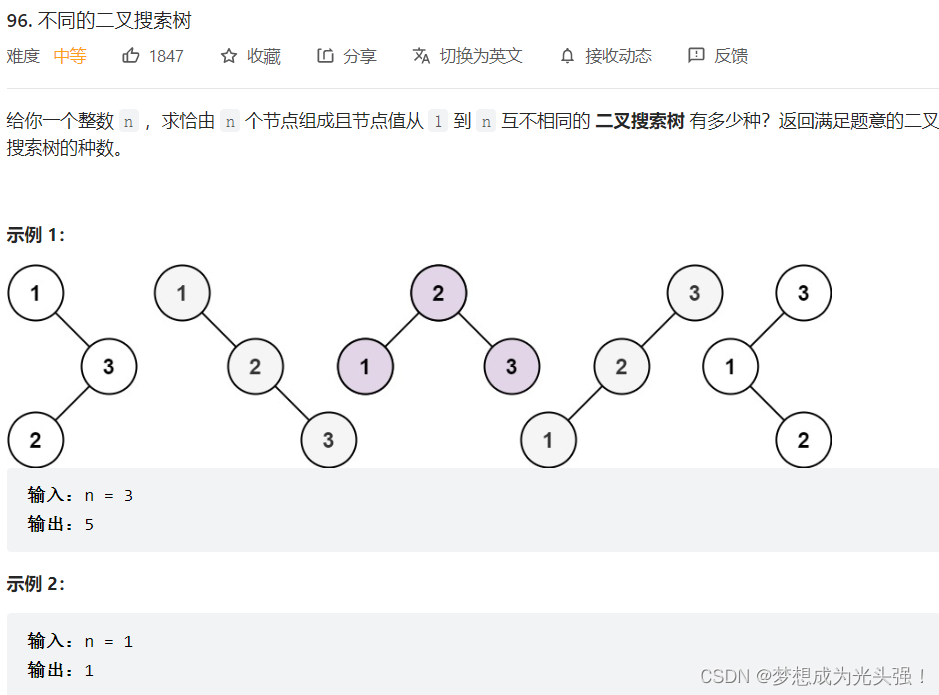
这样子看,既然它说要计算不同二叉搜索树的个数,所以是不是可以定义两个函数。
1.G(n):长度为n的序列可以构成的不同二叉搜索树的个数
2.F(i,n):以i为根丶序列长度为n的不同二叉搜索树的个数(1 <= i <= n)
所以关键点是什么呢?是不是就是G(n)?比如说n等于7,求G(7)怎么搞?是不是就是
F(1,7) + F(2,7) + ... + F(7,7)
那么问题就简化了,然后我们随便拿一个来说,比如F(3,7)。以3为根节点,左子树就两种个,问题是右子树,你怎么知道[4,7],能构成多少个二叉搜索树呢?然后再仔细一思考,这是不是G(4)?也就是长度为4的序列可以构成多少个二叉搜索树呢?对呀,我能不能构成二叉搜索树在这道题里面其和数字范围没关系啊,[1,4]和 [5,8]这两个能构成的二叉搜索树的个数相同吧?
所以转化之后你就会发现
F(3,7) = G(2) * G(4)
是不是就有公式:
F(i,n) = G(i - 1) * G(n - i)
而又因为
G(7) = F(1,7) + F(2,7) + ... + F(7,7)
所以最后其实是14个G(i,n)的计算。然后考虑一下临界情况,也就是一边没有节点或者节点为1的情况,这种的话统一就是一种情况,下面给出代码
public class 不同的二叉搜索树 {
public int numTrees(int n) {
int[] dp = new int[n + 1];
dp[0] = 1;
dp[1] = 1;
for (int i = 2; i <= n; i++) {
for (int j = 1; j <= i; j++) {
dp[i] += dp[j - 1] * dp[i - j];
}
}
return dp[n];
}
}