一、分析算法的引入(RAM模型)
1、RAM模型是什么?
名为随机访问机,是一种我们假定的通用的单处理器计算模型,RAM中的指令是一条一条执行的,没有并发操作。
2、为什么要有RAM模型?
因为利用我们假设的RAM可以在理论上分析算法需要的资源。
3、RAM模型有哪些特性?
?(1)其中指令包括算术指令(加减乘除等)、数据移动指令(装入、存储、复制)、控制指令(条件与无条件转移、子程序调用与返回),每条指令所需时间均为常量。
(2)数据类型有整数型、浮点实数型。
(3)采用RAM模型时分析很简单的算法有时也是一种挑战,需要很多数学工具。
二、插入排序算法的分析
在插入排序时,其运行的时间取决于输入的数字多少,1000个数字排序显然会比3个数字所用的时间长,因此我们引入两个概念,输入规模和插入排序。
1、输入规模和运行时间
(1)输入规模(input size):依赖于研究的问题。比如待排序的数组输入规模为n,若算法输入为一个图,那么输入规模可以用顶点数和边数描述。
(2)运行时间(running time):指执行的基本操作数或者步数,在这里假定每一行伪代码所需要的时间Ci,且注释不需要运行时间。
2、具体分析

注:第五行的tj表示第五行while执行的次数
?对times列求和得到总时间: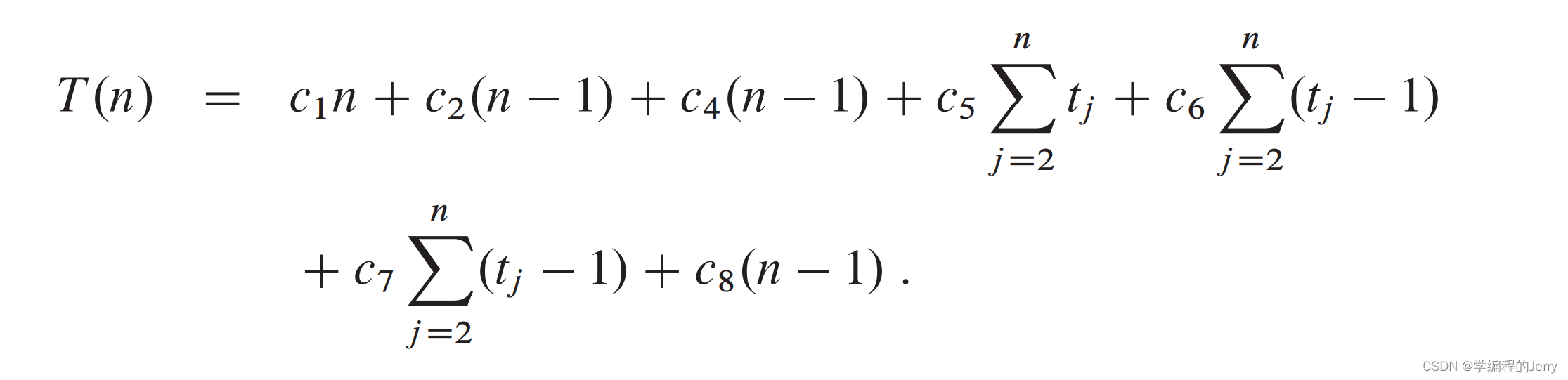
?这是一个一次函数,我们可以将其表示为T(n) = an + b,?其中a和b依赖于Ci。
3、最好情况:数组已经排好序
在for的每一次循环中,while也只需执行一次,因此当j=2,3....n时,tj均等于1
所以能够算出最佳情况运行时间:
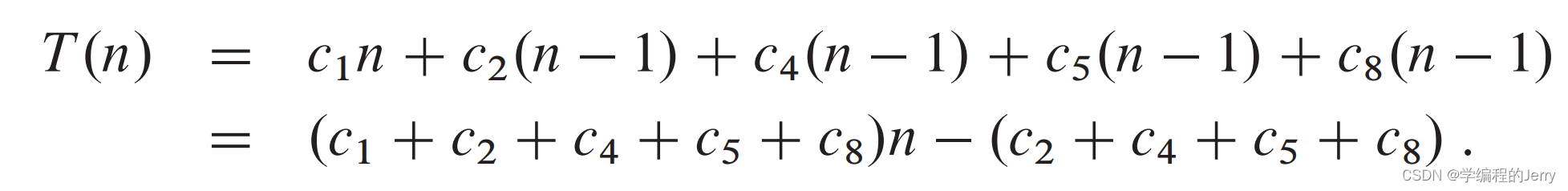
4、最坏情况:数组反向排序
每个元素A[j]都必须和已排序好数组里的每一个数字比较,比如j = 2时,while执行2次(i = 1、0);j?= 3时,执行3次(i = 2、1、0),因此第五行执行次数为(等差数列求和):
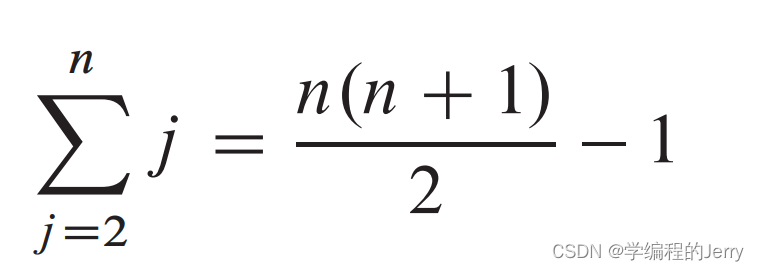
?第六七行执行次数为:
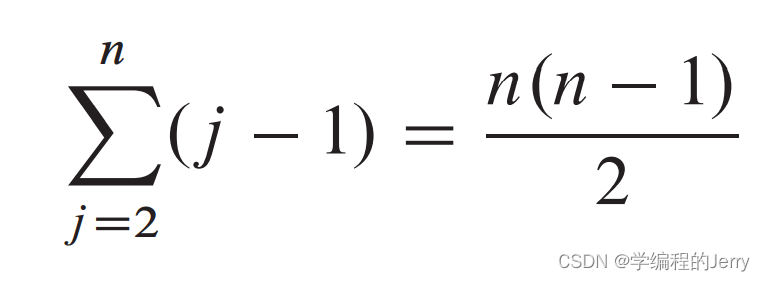
?通过求和得最坏情况总时间:
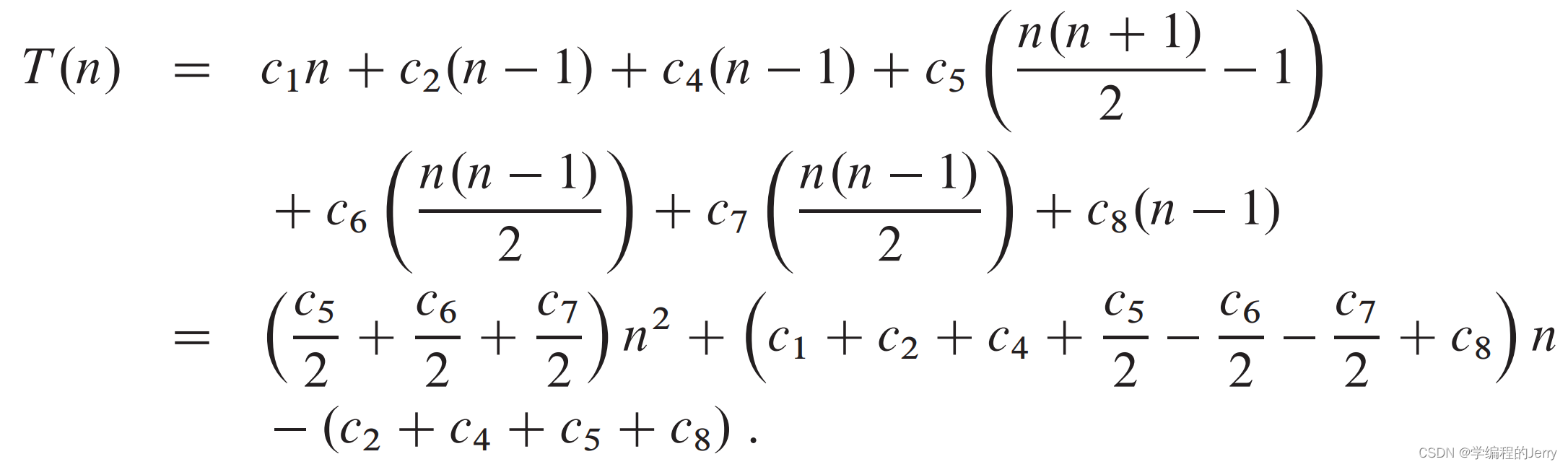
?这是一个二次函数,我们可以将其表示为T(n) = an2 + bn + c,?其中a、b、c依赖于Ci。
?
5、平均情况和最坏情况的分析
平均情况:一半元素小于A[j],一半元素大于A[j](A[j]指待排序数)。
为什么说平均情况和最坏情况差不多糟糕?
因为平均情况中只能将最坏情况的j变成j/2,即while执行j/2次,其本质依旧是二次函数,所以相比最佳情况也是非常糟糕的情况。
6、增长量级(order of growth)
(1)低阶项在n的值较大时远没有高阶项重要,因此我们只需要上面T(n)中的高阶项,比如最坏情况中我们只要an2。
(2)记插入排序最坏情况的运行时间为?Θ(n2)。
(3)在最坏情况下,增长量级小的算法比增长量级更大的算法运行速度更快。如Θ(n2)<Θ(n3)
三、Exercise
2.2-1??Θ(n3)
2.2-2?
for i=1 to A.length-1
min=i //min为最小数字所在位置
for j=i+1 to A.length
if A[j]<A[min]
min=j
//交换
temp=A[min]
A[min]=A[i]
A[i]=temp
可以发现,最好和最坏情况都是需要内外两个for循环一一执行下来的,因此运行时间均为Θ(n2)
2.2-3
for i = 1 to A.length
if A[i] == v
return i //查找到返回i
return NIL在线性查找中,最好情况是一次就找到:O(1)
最坏情况是不包含这个元素:O(n)
下面计算平均情况:1次到n+1次求和,然后除以n+1种可能(需要查找1次到n+1次)
[1+2+3+..+(n+1)]/(n+1) = (n+2)/22.2-4?
略