前言

面试前自己不太熟的算法相关知识点，需要巩固

一、排序

1.有哪些排序算法，排序算法的稳定性、空间复杂度和时间复杂度

算法总结

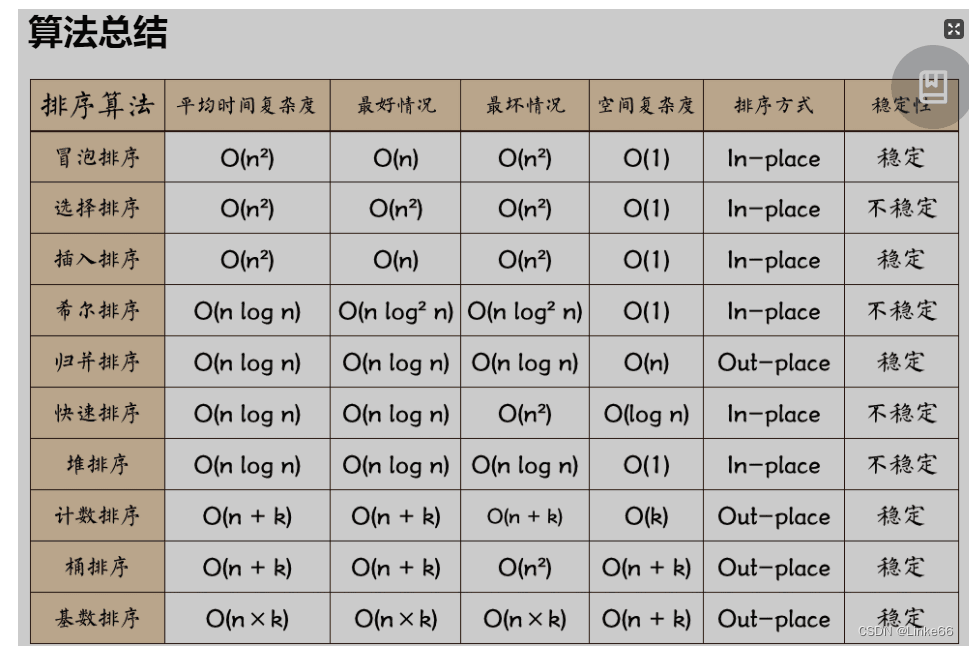
2.常考排序算法代码实现

冒泡排序
算法描述：选取最大元素放到相应位置，一共进行n-1轮。

void BubbleSort(vector<int>& nums) {
	int n = nums.size();

	for (int i = 0; i < n - 1; ++i) {
		for (int j = 0; j < n - 1 - i; ++j) {
			if (nums[j + 1] < nums[j]) {
				swap(nums[j], nums[j + 1]);
			}
		}
	}
}

插入排序
算法描述：找到当前元素在已排序序列中的位置，并插入。

void InsertSort(vector<int>& nums) {
	int n = nums.size();

	int j, cur;
	for (int i = 1; i < n; ++i) {
		j = i - 1;
		cur = nums[i];
		while (j >= 0 && nums[j] > cur) {
			nums[j + 1] = nums[j];
			--j;
		}
		nums[j + 1] = cur;
	}
}

归并排序
算法描述：分治的思想，先分再合。

void __Merge(vector<int>& nums, int p, int q, int r) {
	//临时数组
	vector<int> tmp(r + 1 - p, 0);

	//设置各个起点
	int i = p, j = q + 1, k = 0; 
	
	//合并两个有序数组
	while (i <= q && j <= r) {
		if (nums[i] <= nums[j])
			tmp[k++] = nums[i++];
		else
			tmp[k++] = nums[j++];
	}

	int start = i, end = q;
	if (start > end) {
		start = j;
		end = r;
	}

	while (start <= end) {
		tmp[k++] = nums[start++];
	}
	
	//将排序好的数据拷贝到原始数组中
	int n = tmp.size();
	for (int c = 0; c < n; ++c) {
		nums[c + p] = tmp[c];
	}
}


void __MergeSort(vector<int>& nums, int p, int r) {
	//终止条件
	if (p >= r) return;

	//求分界点
	int q = p + (r - p) / 2;

	//先分
	__MergeSort(nums, p, q);
	__MergeSort(nums, q + 1, r);

	//再和
	__Merge(nums, p, q, r);
}

void MergeSort(vector<int>& nums) {
	__MergeSort(nums, 0, nums.size() - 1);
}

快速排序
算法描述：先分再合，每次分的时候，随机选取键值，将比键值小的元素分为一块，比键值大的元素分为另一块。

int __Partition(vector<int>& nums, int p, int r) {
	//随机选取键值
	int random_idx = rand() % (r + 1 - p) + p;
	swap(nums[r], nums[random_idx]);
	int pivot = nums[r];

	//比键值小的元素分一块，大的另一块
	int i = p;
	for (int j = p; j <= r - 1; ++j) {
		if (nums[j] < pivot) {
			swap(nums[i], nums[j]);
			++i;
		}
	}
	swap(nums[i], nums[r]);

	//返回分界点
	return i;
}

void __QuickSort(vector<int>& nums, int p, int r) {
	//终止条件
	if (p >= r) return;

	//先分
	int q = __Partition(nums, p, r);

	//再合
	__QuickSort(nums, p, q - 1);
	__QuickSort(nums, q + 1, r);
}

void QuickSort(vector<int>& nums) {
	__QuickSort(nums, 0, nums.size() - 1);
}

堆排序
算法描述：如果是升序排序，使用数据结构大顶堆，每次将堆顶元素取出放到数组末尾位置end，并且end-1；每次操作都要重新调整堆。

//end为尾后下标
void Sink(vector<int>& nums, int start, int end) {
	int parent = start;
	int children = parent * 2 + 1;
	while (children < end) {
		if (children + 1 < end && nums[children + 1] > nums[children]) {
			++children;
		}

		if (nums[children] > nums[parent]) {
			swap(nums[children], nums[parent]);
			parent = children;
			children = 2 * parent + 1;
		}
		else {
			break;
		}
	}
}

void HeapSort(vector<int> &nums) {
	int n = nums.size();

	//建堆
	int i;
	for (i = n / 2 - 1; i >= 0; --i) {
		Sink(nums, i, n);
	}

	//开始排序
	int end = n - 1;
	while (end) {
		swap(nums[0], nums[end]);
		Sink(nums, 0, end);
		--end;
	}
}

3.什么时候用快速排序，什么时候用插入排序？

大多数实际情况中，快速排序是最佳选择；
（算法第4版159页）但是对于小数组或者基本有序的数组，使用插入排序会效率更高。

4.快速排序什么情况下会有最坏的时间复杂度？如何优化？

当每次选取的键值都是最小或最大元素时，每次分块都是一边为空，一边size减一，使得快速排序的时间复杂度变为O(n²)。

改进方法：
三取样切分法（算法第4版187页），改进快速排序性能的一个方法是使用子数组的一小部分元素的中位数来切分数组。这样做得到切分更好，但代价是需要计算中位数。人们发现（经验）取样大小设为3并用大小居中的元素切分的效果更好。
比如可以选择首元素、尾元素和一个随机元素，然后选取三个数的中位数作为键值，这样就可以基本避免最坏时间复杂度的情形发生。

二、图论

1.并查集

并查集用来解决什么问题？
并查集一般用来解决连通性问题，能够判定图中的两个节点是否相连，即能否从一个节点走到另一个节点，但是并没有要求给出两者之间的连接的情况。
通俗来讲，并查集就是用来分门别类的，随机给定两个点，通过并查集的Find接口就可以判断它们是否连通。

并查集的核心代码

const int N = 100;
int father[N];

void Init() {
	//每个节点初始化为自己
	for (int i = 0; i < N; ++i) {
		father[i] = i;
	}
}

int Find(int x) {
	//查找主元，并且在查找的过程中进行状态压缩
	if (x != father[x]) {
		father[x] = Find(father[x]);
	}
	return father[x];
}

bool Union(int x, int y) {
	int fx = Find(x), fy = Find(y);

	if (fx == fy) return false;

	//合并
	father[fx] = fy;
	return true;
}

2.最小生成树

**练习题：**力扣1584.连接所有点的最小费用

Prim算法
算法思想：从集合U的点中选取一条权值最小的边作为起点u，并且将u能走到的所有点v加入集合U。往复此操作。

Prim算法模板

    #define maxn 1000
    int matrix[maxn][maxn];
    int vi[maxn];
    int cost[maxn];
    
    int Prim(int n){
        cost[0] = 0; //起点

        int i, j, u, v;
        int min_cost;
        int sum = 0;
        for(i = 1; i <= n; ++i){
            min_cost = INT_MAX;
            for(j = 0; j < n; ++j){
                if(!vi[j] && cost[j] != -1 && cost[j] < min_cost){
                    min_cost = cost[j];
                    u = j;
                }
            }

            if(min_cost == INT_MAX) break;
            sum += min_cost;
            vi[u] = 1;

            for(v = 0; v < n; ++v){
                if(!vi[v] && matrix[u][v] != -1 && (cost[v] == -1 || cost[v] > matrix[u][v])){
                    cost[v] = matrix[u][v];
                }
            }
        }
        return sum;
    }

Kruscal算法
算法思想：将所有边进行升序排序，然后利用并查集，如果两点连通就跳过，否则就加入最小生成树。

Kruscal算法流程
1 Edge(u, v, w)放进数组中并按w进行排序
2 遍历数组，查看u和v是否在一个连通域中，不是则将这条边加入最小生成树

3.最短路径

Dijstra算法

Floyd算法

SPFA算法

三、高级数据结构

1.字典树

2.跳表

3.树状数组

4.AVL树、红黑树、B+树

三、力扣需要巩固的题

1.HOT100

46.全排列（递归和非递归做法）
56.合并区间（按左界排序，然后用当前区间与ans最后一个区间右界比较）

2.剑指offer

3.其他

25.K 个一组翻转链表（考察链表操作，就是复杂）
41.缺失的第一个正数（原地哈希）
43.字符串相乘（记大数相乘流程）
69.x的平方根（二分法）
93.复原IP地址
129.求根节点到叶节点数字之和(DFS)
138.复制带随机指针的链表（链表操作）
145.二叉树的后序遍历（迭代法）
162.寻找峰值（二分，爬坡法，与mid + 1比较）
165.比较版本号（模拟，记方法）
224.基本计算器 (利用栈模拟，记思想）
227.基本计算器II（利用栈模拟，记思想，需要一个pre_sign变量）
468.验证IP地址（回溯）
470.用Rand7()实现Rand10() (用平方做，撒豆子）